A graph is a kind of data structure that includes a set of vertices and edges. Graph traversing means a visit to each vertex of the graph precisely. The graph traversing is used to determine the order in which vertices are being visited throughout the search process. A graph traversing searches for the edges that will be used in the search operation without establishing loops. This means that using graph traversal, we will go to all the vertices of the graph without going into a looping path.

There are two kinds of graph traversal methods.

• Breadth-First Search

• Depth First Search

Breadth-First Search (BFS)

Breadth-first search is also called a level order traversal. Breadth-first search is an algorithm to traverse the graph level by level. In the traversing process, we have to visit all vertices and edges. In this, we can take any node as a root node during traversal starting. For BFS, a queue data structure would be used that follows FIFO(First In First Out) principle. We visit nodes level wise. First, we complete the top level and then move on to lower levels.

In breadth-first search, we identify the levels in the graph and then we visit or traverse all the vertices. Breadth-first search is level by level exploration of the graph.

Implementation of Breadth-First Search

The implementation of breadth-first search involves the following steps:

• We take input as a graph to traverse it.

• For all edges incident on that vertex, we are going to check to see whether it is undiscovered or not. If it is an undiscovered edge, we check the vertex follows the undiscovered edge. If that vertex is visited, we mark the edge as a cross edge. If that vertex is not visited then we mark the edge as a discovered edge. We visit that vertex and add that vertex to the next level. Once none of the vertex incidents on the vertex is undiscovered, we start to explore the next vertex.

Example

Let us consider a graph shown below to traverse. At the beginning of the breadth-first search, all the vertices are going to be unvisited and all the edges are going to be undiscovered. So, we will symbolize the unvisited vertex by ( O ) and the undiscovered edge by ( / ).

Now we select an arbitrary vertex (A ) as a starting vertex and visit it. Then we set its level as 'Lo'. At zero level (Lo), we have one vertex (A).

For all vertices in level zero, we will go to each undiscovered edge. Every undiscovered edge follows with another vertex. For the vertex that follows is unvisited, then we will visit that vertex and add it to the next level. And if that vertex is visited then we will set the edge to be a cross edge.

Now we go to the first undiscovered edge 'B' and make it discover edge from the discovered vertex 'A'. Discovery edge is represented by black dotted lines. Similarly, we visit undiscover edges C and D and make them discovered edges.  Also, we add B, C and D edges to level 1 (L1).

Now there are no more edges to traverse for Lo. So, we can go to the next level L1. Now we will go through each vertex of L1. At vertex B, we go to each of the undiscovered edges. From vertex B, we will reach vertex C which has already been visited. So now we will set edge C as a cross edge. The cross edge is represented by the blue line.

Now, we go to undiscovered edge E from vertex B.E is the unvisited vertex. So we visit the vertex E and discover the edge. Then E has added to Level 2 ( L2 ) and comes back to B.

Then we go to vertex C where there are three undiscovered edges( E, F and D ). As E is already visited, so we make it cross edge with a blue line. Now we will go to vertex F that is unvisited, so we make this edge a discovery edge. Now we go to edge D that is already visited, so we make it cross edge.

Now D has left one undiscovered edge F. It can be observed that F has been already visited so it will become cross-edged with D.

Next, we go to level L2 that contains E and F vertices. On E, there are no undiscovered vertices. Now we go to F where there are also no undiscovered vertices. So now level L2 will also complete. So, now traversing has been completed. And the breadth-first search has been done.

Pseudocode

Let us consider Graph 'A' as input and called our algorithm BS. Firstly, we will define all vertices are unvisited and all edges are undiscovered.

BS(A){
	for all v  A.vertices{
		setlabel( v , UV )   
	}
	for all e  A.vertices{
		setlabel( e , UD )   
	}
	for B A.vertices{      
    list.addEnd(B);
    setlabel(B,V);  
  }      
	while ( list.Notempty( ) ){
		v = list.removeFront( );
  }
	for e A.incident on v{
		if ( e.label == UD ){
				q = adjvertex(v,e);
    }
		if ( q.label = V ){
				setlablel( e, cross);
		}
		if ( q.label == UV ){
				setlablel( e, D);  
				setlabel( q , V );
				list.addEnd(q);
		}
	}
}

Time Complexity of Breadth-First Search

Its time complexity is 

b^x

Where b represents the branching factor and x is level.

Space Complexity of Breadth-First Search

Its space complexity is :

b^x

Where b represents the branching factor and x is level.

Advantages of Breadth-First Search

It has the following advantages:

• BFS will not get trapped exploring visually impaired search.

• If there are several solutions, then it will give a cost-efficient solution because a longer route is never investigated until all shorter paths are already available.

• With this search method, we can find the final solution without examining very much of the search room at all.

Disadvantages of Breadth-First Search

It has the following disadvantages:

• The amount of time required to produce all the nodes is to be taken into consideration because of time complexity.

• It uses plenty of memory space.

Applications of Breadth-First Search

It has the following applications:

• It is used to find the shortest path in the undirected graph.

• It is used in cycle detection.

• It is used in the bipartite check.

• It is used in social networking websites and GPS navigation.

Depth First Search (DFS)

It is a way to traverse the graph. In this, we visit all the vertices and edges and traverse the graph. In depth-first search, the stack data structure is used that follows the LIFO( Last In and First Out) principle. Depth-first search produces a non-optimal solution. In depth-first search, we keep on exploring or visiting vertices till we reach a dead-end where there are no more edges to traverse from that vertex and then we backtrack.

Implementation of Depth First Search

Implementation of depth-first search involves following major steps:

• Firstly select an arbitrary vertex and make it the current vertex by visiting it.

• Then look for undiscovered edges corresponding to the current vertex.

• On finding the undiscovered edge, we see whether the vertex that follows is an unvisited vertex or not.

• If it is an unvisited vertex, we set a discovery edge and then go to that vertex.

• If it is a visited vertex, we set it as a back edge.

• If there is no undiscovered edge found, we must backtrack.

Example

Let us consider the graph shown below. Initially, all the vertices are unvisited, and all edges are undiscovered. In this graph, we have represented an unvisited vertex by a circle and undiscovered edge by a single line.

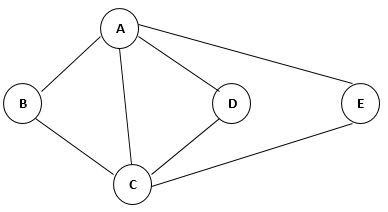
Firstly, we choose an arbitrary vertex A and visit it. The visited vertex is represented by a green circle while the current vertex by a red circle.

Now we look for corresponding edges of vertex A. Vertex A has four undiscovered edges B, D, C and E. From the current vertex A, we will take B as an undiscovered edge and visit it. Then we will set the edge traversed to discovered. Then B will become the current vertex after visiting it. And edge between A and B will become discovered edge that is represented by a dotted line.

Now from current vertex B, there is one undiscovered edge C. So we will visit C and discovered it. Then C will become the current vertex.

Now, we will look for undiscovered edges from current vertex C. If we consider a discovered edge from C to A, it can be seen that an undiscovered edge is leading to an already visited vertex. If the vertex that follows the undiscovered edge is visited, then mark the edge as the back edge. And back edges are represented by a blue colour line. So, the edge between A and C will become a back edge.

From current vertex C, we move on to visit undiscovered edge D and make it visited. Now D will become the current vertex.

From D, there is one undiscovered edge A, but it reaches the visited vertex. So we will convert this edge into a back edge.

Now from current vertex D, there is left no undiscovered edge. So in such a case, we will set current vertex C which is the parent vertex of D.

From current vertex C, we have one undiscovered edge E. So we will visit vertex E and it will become the current vertex.

Now from vertex E, there is one undiscovered edge A. As vertex A has been already visited. So edge between E and A will become a back edge.

Now we will backtrack from E to C because E has left no undiscovered edges.

Now we will backtrack from C to B because C has left no undiscovered edge.

Now B has left with undiscovered edges so we will backtrack from B to A. Now all the vertices have been visited. And traversing has been completed.

Pseudocode

Let us consider Graph 'A' as input and called our algorithm DS. Firstly, we will define all vertices are unvisited and all edges are undiscovered.

DS(A){
  for v  A.vertices{
    setlabel ( v, UN ); 
	}
	for e  A.edges{
		setlabel ( e, UD );
	}
	for v  A.vertices{
		visit( v, A) ;
  }
	setlabel ( v , V ); 
	for e  v.incidentEdges{
		if(e.label == UD){
			q = adjacentVertex ( v, e );
    }
		if(q.label == UV){
			setlabel(e, D);  
			visit( q, A);
		}
		if(q.label == V){
			setlabel(e, B);  
		}
	}
}

Time Complexity of Depth First Search

Its time complexity is 

O(n^x)

Where n represents the number of nodes at level x.

Space Complexity of Depth First Search

Its space complexity is

O(n*x)

Where n represents the number of nodes at level x.

Advantages of Depth First Search

It has the following advantages:

• It needs less amount of memory because just the nodes on the current path will be stored.

• With this search method, we can find the final solution without investigating very much of the search space at all.

Disadvantages of Depth First Search

It has the following disadvantages:

• DFS cannot find many a satisfactory solution if they exist.

• Cut of depth, we have to define otherwise DFS goes in an infinite loop.

Applications of Depth First Search

It has the following applications:

• It is used to find a minimum spanning tree.

• It is used in cycle detection.

• It is used in the bipartite check.

• Also used to check the path between two nodes.