Asymptotic notations are used to represent the complexity or running time of an algorithm. It is a technique of defining the upper and lower limits of the run-time performance of an algorithm. We can analyze the runtime performance of an algorithm with the help of asymptotic notations. Asymptotic notations are also used to describe the approximate running time of an algorithm.
Types of Asymptotic Notations
Following are the different types of asymptotic notations:
Big O Notation (O)
Big Omega Notation( ?)
Theta Notation ()
Need of Big O Notation
We can use Big O notation to compare and search different solutions to find which solution is best. The best solution is one that consumes less amount of time and space. Generally, time and space are two parameters that determine the efficiency of the algorithm.
Big O Notation tells accurately how long an algorithm takes to run. It is a basic analysis of algorithm efficiency. It describes the execution time required. It depends on the size of input data that essentially passes in. Big O notation gives us algorithm complexity in terms of input size. For the large size of input data, the execution time will be slow as compared to the small size of input data. Big O notation is used to analyze space and time.
Big O notation gives us the growth of the time. Big O notation of a particular function gives us the order of the growth of that function. It is used to tell the relative efficiencies of algorithms in terms of space and time. It makes us understand the execution time and the main requirement of the function of increasing input size.
If f(x) is a function , then there exists a function g(x) such that g(x) is greater than or equal to f(x) for all points x , where x is greater than x0:
We can say that f(x) is O(g(x)). This is Big O Notation of f(x). In its notation, 'O' stands for the order of magnitude. Big O notation represents the upper bound of an algorithm running time. Upper bound means maximum running time. It represents the worst case of an algorithm time complexity that is the largest amount of time an algorithm can take to for execution.
Types of Measurement
Following are the different ways to measure the algorithm efficiency such as:
Average Case
It is the average time required for the execution of an algorithm.
Worst Case
It is the maximum time required to execute an algorithm. It tells us how slow an algorithm can execute.
Best Case
The best case is the minimum time required for the execution of an algorithm. It tells how fast an algorithm can execute.
Example
To understand the above cases, let's consider an array:
If we want to search for 2 in an above array and on comparing we found that element in the first position. Then it would be the best case because it requires minimum time.
If we want to search for 6 in the above array. Then we need to perform a comparison with each value in the array and it will require maximum time. So it would be the worst case.
If we need to find element 4 in a given array, then it would require an average time to perform comparison or execution. So this would be an average case.
When we talk about Big O notation, we typically look at the worst case.
Working Principle
To understand its working principle, the following things must be remembered while calculating running time :
We will ignore constants when there is a product of multiple terms. Because the run time of constant is only unit time. For example, if we have a function
This function will execute 'n' times. So, in this function 'n' matters, not 8. So constant '8' will be ignored from this function. In this way, the run time complexity of this function will be 'On'
2. If the Big O is the sum of several terms then only keep the largest term and left the rest of the terms. For example, if we have :
In this, we have two terms. Among these two terms, we will select the largest term. So here, just 'n' is the largest term because 900 is a constant value. So, its complexity is 'O(n)'. Similarly, if we have an expression like :
Then its complexity will be 'O(n2)'.
3. In the case of unsimplified Big O expressions such as:
After dropping out constant values from these expressions, we have:
4. Certain terms will dominate in it. Big O notation will be in this order:
O(n) has the smallest order due to less running time as compared to others. As the size of 'n' terms increase, running time will increase. So, higher-order terms have high running time. So ignore the low order terms as 'n' increases.
Time Complexity Analysis
Time complexity is a mathematical technique of showing how the runtime of a function rises as the size of the input increases. Time complexity gives us an idea about how function scales as input to the function gets larger. When the input size is small, the function will take less time. In time complexity analysis, firstly we have to understand the following terms:
Constant Time
In this, the time taken to complete a function does not increase with size but it remains constant. Big O notation of a constant time is always one. If we have some function x=6*5; In this function, there is going to be no input to this function. So, its runtime is 1, and time complexity will be 'O(1)'.
Linear Time
In this, as the size of the input increases, time increases linearly with size. If we have a linear function f(x)=3x-1. And the value of x is in the range of 0 to n. This function will execute for 0 to n values. So in this way, the complexity of linear time will be 'O(n)'. The expression O(n) will be read as ‘’
Quadratic Time
In this, the time taken to complete a function increases with size in a quadratic manner. If we have a quadratic function f(x) = 5x2 + 4y + 1.Value of x and y in the range of 0 to n.
So the time complexity will be 'O(n2)'.
Big O Notation Worst-Case Complexity
For all positive values of n, if g(n) is a function.
Where there exists constants c and n0, such that
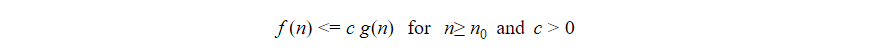
To understand this, let us consider an example in which we have the following function:
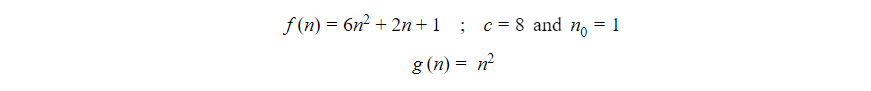
The value of f(n) will always be less than and equal to g(n2). So this function will work in the following way:
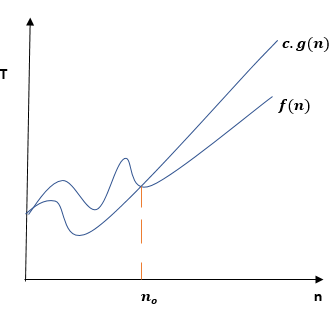
Graph
Let us consider the following graph. In this graph, the x-axis represents input size (n) and the y-axis represents time growth (T) of an algorithm. Time growth (T) increases with input size(n). Suppose that f(n) is a particular function with respect to the input side in this graph. For representing the upper bound, we plot a function 'c.g(n)'. The value of function f(n) will not go above 'c.g(n)'. The value of f(n) is always less than or sometimes equal to c.g(n).
Example 1
Let us consider an array from 1 to 10
Firstly, a function will be defined which will take an array ‘A' and find the sum of elements in the array. Inside this function, variables will be initialized. For each value of 'k' in this array, elements will be going to add in the variable 'total'. In this way, the sum of all elements will be found in this array.
def find_sum(A);
total = 0 ;
for ( k=0 ; k<=n; k++){
total = total + k ;
}
return totalThe run time of this function is based on the size of the input. For the Big O , find the fastest growing term and then take out the coefficient . Suppose , if the fastest growing time is
Where 'T' is the time taken to run the function. Then coefficient will be taken out as
If we have two functions and one of them executes at constant time and the other one takes linear time. The first function will take O(1) and the second function will take O(n) time. On comparing these two functions, it can be concluded that the second function will take more time. O(1) is better than O(n) because it takes less time to execute.
Example 2
Let us consider another array
Now we will determine the time complexity and Big O notation without any experiment.
def find_sum(B);
total = 0 ;
return total;In above code, time taken to execute 'total=0 ' is O(1) and it will also be same for 'return total'.
Time taken to execute the entire function is

Example 3
Now let us consider another example in which we have taken the following array:
def find_sum(C)
total = 0
for ( each f in C)
total = total + f;
return total;Now to find the Big O notation and time complexity of this function, the execution time will be analyzed. As the variable 'total ' takes an equal amount of time at every time. So, it has time complexity as 'O(1)'. And 'return total' will also have the same time complexity. Time taken will be
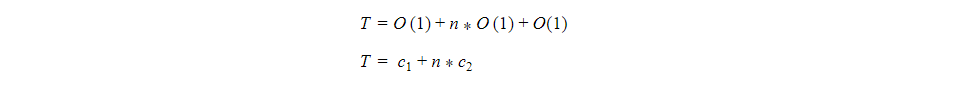
In the above expression, c2 is the fastest-growing term.
Example 4
Let us consider another example related to quadratic time. For this purpose, we consider a two-dimensional array that is:
In this array, we have a total of nine elements. As the number of columns is equal to the number of rows in this array so we have 'n2' elements in this array. Now we will define a function that will find the sum of elements of this array. Then define a variable 'total' and assign a value equal to zero. Then a double for loop will be executed. In the for-loop, variable 'i' represents the element in each row.
def find_sum(B)
total=0;
for ( Each i in row of B:)
total = total + i ;
return total;Now for finding the time complexity and Big O notation , it can be seen that time taken to execute complete function is :
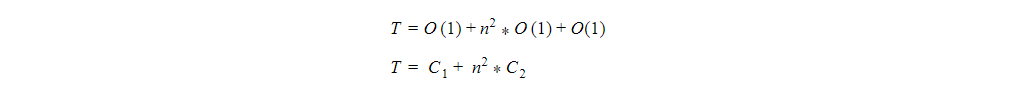
The fastest growing term in above expression is C2.
Space Complexity Analysis
In space complexity analysis, we take a look at how much memory or space is used. For this purpose, let’s consider an example. We have created the sum variable ‘S’ and assigned its value to zero. In for loop, we initialize a counter variable only at once for the entire loop. On looking at the inner variable 'number=numbers[i]', this will execute on every single iteration of this for a loop. Once this iteration is finished, memory will be freed for this variable. As this entire loop runs it's not as if each of these number variables is going to persevere in memory. Space complexity will be only 'O(1)'
const cal_avg = (num){
S=0;
for ( i=0 ; i < num.length ; i++){
num= num[i];
S= S+ num;
}
return S /num.length;
}; Properties of Big O Notation
It has the following properties:
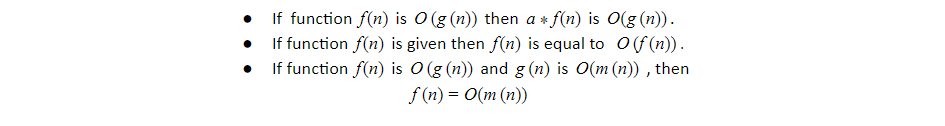
Application of Big O Notation
Following are the applications of Big O Notation:
It is used to quickly compare multiple functions in terms of their performance.
Also used to analyze the execution time of an algorithm