Давайте представим, что нам пришла задача построения уравнения регрессии, но с одним уточнением - нам точно известно, что зависимая переменная находится в интервале [0;1]. Что изменится? Давайте посмотрим, что про это говорили ученые из университета португальского города Эворы (doi: 10.1111/j.1467-6419.2009.00602.x; doi: 10.1111/manc.12032).
Минутка теории
Как правило, для решения поставленной выше задачи используются три основных метода:
-
Мы просто не обращаем ни на что внимание, и строим обычную модель регрессии, находя вектор параметров θ
![Основной недостаток - прогнозируемые значения y могут выходить за пределы интервала [0;1] Основной недостаток - прогнозируемые значения y могут выходить за пределы интервала [0;1]](https://habrastorage.org/getpro/habr/upload_files/819/7c8/aa1/8197c8aa1a7bce42cc1f4806fe2183d4.png)
Основной недостаток - прогнозируемые значения y могут выходить за пределы интервала [0;1] -
Мы применяем нехитрое преобразование типа

Но в этом случае интерпретация параметров регрессии θ может превратиться в достаточно увлекательный квест, это раз, и, во-вторых, модель будет ошибаться в граничных точках Применять модель тобит-регрессии при большом количестве граничных наблюдений, но стоит помнить, что ее оценки могут быть смещены при нарушении условий Гаусса-Маркова
Для задачи регрессии, в которой зависимая переменная находится в диапазоне (0;1), данные проблемы решаются применением одного из двух методов:
-
При неизвестном распределении зависимой переменной строится модель
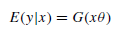
где G() - нелинейная функция (чаще всего это логит-, пробит-функция, функция Коши, лог-логистическая функция, функция Гомпертца) При этом, оценка параметров θ производится по методу квазимаксимального правдоподобия и полученные оценки являются эффективными
При известном распределении зависимой переменной можно построить модель с учетом этого (например, модель бета-регрессии)
В рассматриваемых работах предложена двухкомпонентная модель регрессии, в которой используется и тот, и тот подход, а также разработаны некоторые особенные тесты спецификации модели для зависимой переменной, находящейся в любом из данных интервалов: [0;1), (0;1], [0;1].
То есть, например, для интервала [0;1) вводится новая переменная

Предложено также семейство статистических тестов (GOFF1, GOFF2, GGOFF) для проверки правильности спецификации данных моделей. Отличия тестов - в рисунке ниже

Теперь давайте попробуем применить все это на практике
Методология
Возьмем данные по индексу человеческой свободы за 2020 год по странам мира (https://www.kaggle.com/gsutters/the-human-freedom-index) и попытаемся построить модель для одного из индексов (pf_expression_media)
library(tidyverse)
library(ModelMetrics)
library(readr)
library(frm)
Base <- na.omit(read_csv("D:/.../hfi_cc_2020.csv"))
Base <- as.data.frame(Base[, c(6:113)])
y <- as.matrix(Base[,38]/10)
sum(y==0) # 5 наблюдений с значением показателя, равным 0
sum(y==1) # 40 наблюдений с значением показателя, равным 1
X1 <- Base[,c(49,106)] # Первая группа независимых переменных
X2 <- Base[,c(51,55)] # Вторая группа независимых переменныхПостроим простую однокомпонентую модель (и эта модель - модель цензурированной регрессии)
m_1_1 <- frm(y,X1,linkfrac="logit") # Строим логистическую модель регрессииАвтоматически выводится следующее окно по результатам расчетов

Всего можно попробовать 5 разных функций G(), которые дадут разные результаты
m_1_2 <- frm(y,X2,linkfrac="probit")
m_1_3 <- frm(y,X1,linkfrac="cauchit")
m_1_4 <- frm(y,X2,linkfrac="loglog")
m_1_5 <- frm(y,cbind(X1,X2),linkfrac="cloglog")
Теперь построим двухкомпонентную модель
m_2 <- frm(y,X2,X1,linkbin = "cauchit",linkfrac="logit", type = "2P")
# Параметр linkbin отвечает за функцию преобразования первой части модели - модели бинарного выбора
m_2_0 <- frm(y,X1,X1,linkbin = "logit",linkfrac="logit", type = "2P",inflation = 1)
# Параметр inflation = 1, указывает, что на первом шаге строится логистическая регрессия?
# определяющая, равна ли зависимая переменная 1
Теперь поговорим о тестах. RESET-тест спецификации однокомпонентной модели
frm.reset(m_1_1,2:3,c("Wald","LM"))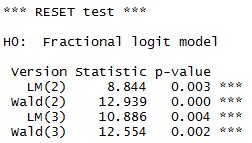
Нулевая гипотеза: спецификация верна, и согласно расчетам, она верна для каждой переменной (нет полиномиальной зависимости)
frm.reset(m_1_5,2:5,c("LM"))
Для этой модели - нулевая гипотеза выполняется для 3 и 4 переменной (по LM-методике расчета), и желательно добавить в БД переменные, являющиеся степенью 1 и 2 переменных
frm.ggoff(m_1_5,c("Wald","LM"))
При этом GGOFF-тест показывает неправильную спецификацию для всей модели в целом
Также пакет frm позволяет сравнивать все модели между собой
frm.ptest(m_1_1,m_1_3)
frm.ptest(m_2,m_2_0)


phanerozoi_evidence
надеюсь статья наберёт лайки. + в карму Вам поставил
acheremuhin Автор
Спасибо на добром слове, Вам тоже успехов.
phanerozoi_evidence
Благодарю=)