
Антон Долгих, руководитель отдела AI, Healthcare and Life Sciences в компании DataArt
В 2020 году мир как будто забыл о сезонном гриппе благодаря пандемии коронавируса. Однако грипп никуда не делся. Некоторые эпидемиологи ожидают вспышку заболеваемости уже в сезоне 2021–2022. Грипп может проявиться агрессивнее, потому что наша иммунная система, привыкшая к ежегодной эпидемии, ослабила хватку. При этом, говорят эксперты, из-за дефицита информации в сезоне 2020–2021 труднее спрогнозировать ситуацию и определить, какие штаммы будут распространяться.
Действительно ли так сложно прогнозировать эпидемию? Ведь мы с гриппом сосуществуем не одно десятилетие, в отличие от COVID-19 и, должно быть, все о нем знаем. Предлагаю разобраться — с минимумом уравнений, без которых никуда, и сложных терминов.
Что такое эпидемия с научной точки зрения
Когда мы слышим слово «эпидемия», обычно представляем нечто с очень серьезными последствиями. То, что точно нельзя не заметить: ежедневные сводки в новостях, скорая помощь с сиренами на улицах, карантинные меры. Но для науки это в целом гораздо менее кровожадное событие.
Среди множества определений «эпидемии» самым популярным в научной среде можно назвать то, которого придерживается CDC. Согласно ему, эпидемия — это увеличение, часто внезапное, количества случаев заболевания по сравнению с тем, которое обычно ожидается для данной популяции в данном районе.
Великая чума в Лондоне, унесшая в 1665–1666 годах жизни 100 тысяч горожан (20 % населения), — эпидемия. Вспышка гриппа в 1978 году в закрытой школе для мальчиков на севере Англии, в результате которой переболело 512 из 763 учеников, — тоже эпидемия. Относительно недавний случай во Франции, когда 7 гостей на свадебной вечеринке заразились вирусным гепатитом E, съев традиционную корсиканскую колбасу из свиной печени (фигателлу), также считается эпидемией.
Огромная доля эпидемий проходит незамеченными для большинства из нас. По данным ВОЗ, с 2011 по 2017 год в мире фиксировалось от 164 до 213 эпидемий: чума, холера, лихорадка Денге, вирус Зика и другие.

Одним словом, эпидемий так много, что логично подходить к ним системно, привлекая математику, чтобы сгладить их последствия.
Вирус гриппа и первая сложность для моделирования
Грипп — вирус, для которого естественным резервуаром являются животные: птицы, свиньи, лошади, люди. Существует четыре типа гриппа: A, B, C и D, из которых у людей встречаются первые три, при этом тип C выявляется редко и обычно безобиден. Самый опасный, приводящий к пандемиям, — вирус группы A. Он подразделяется на подтипы в зависимости от сочетания белков (антигенов) на его поверхности, которые обеспечивают проникновение в клетку человека: гемагглютинина (HA) и нейраминидазы (NA).
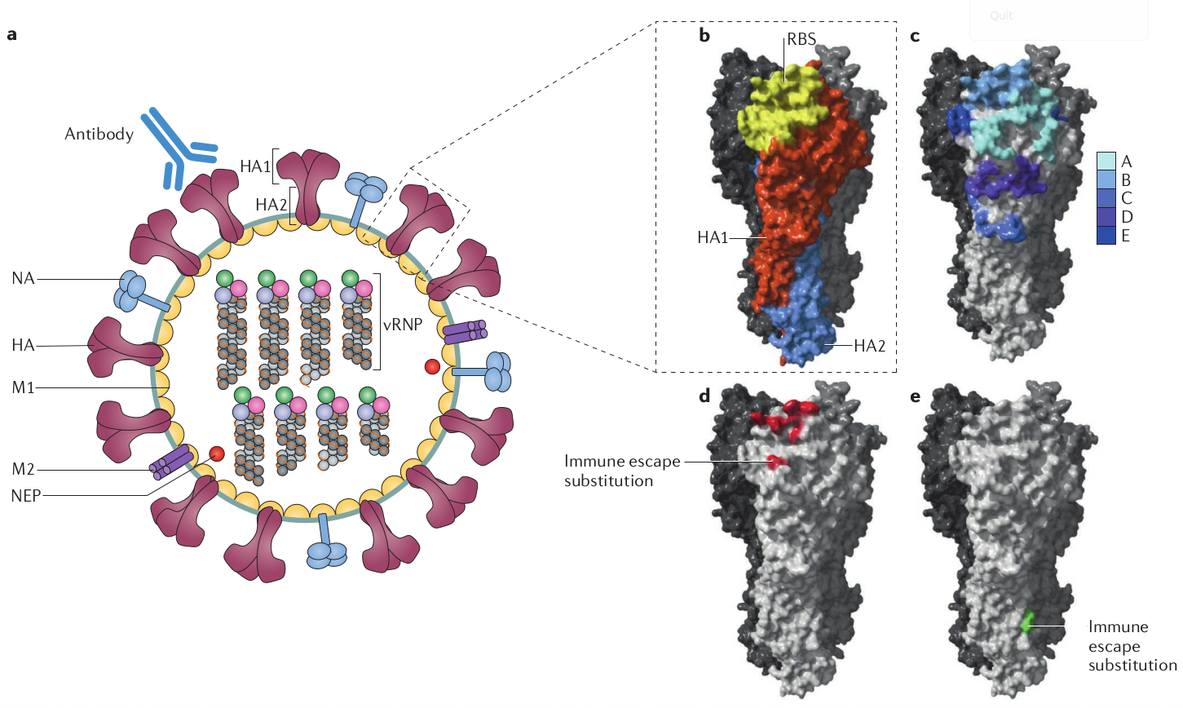
Вы наверняка знаете эти комбинации: H1N1, H3N2, H5N7. Буква «H» здесь — гемагглютинин, а «N» — нейраминидаза. Сейчас известно 18 типов гемагглютинина и 11 нейраминидазы, т. е., например, возможна вариация H18N11.
Важно отметить, что грипп — РНК-вирус, что означает высокую вероятность мутаций. В процессе репликации (копирования) РНК при проникновении в клетку происходит больше количество ошибок из-за изменений в структуре гемагглютинина и нейраминидазы. Грубо говоря, в клетке собирается не тот вирус, который ожидает встретить организм. Это новый штамм, к которому нет иммунитета, даже если организм перенес грипп месяц назад. Запомним эту важную для моделирования особенность.
Самая популярная модель и другие сложности для моделирования
При моделировании, как правило, смотрят на следующие характеристики, которые помогают рассчитать нагрузку на систему здравоохранения:
начало эпидемии;
время наступления пика эпидемии;
интенсивность пика;
количество людей, которые переболеют за время эпидемии.
Для ответа на эти вопросы в 1927 году шотландские ученые Андерсон Кермак и Уильям МакКендрик предложили SIR-модель, которая до сих пор считается базовой. Согласно ей, вся популяция разделена на три группы: восприимчивых к инфекции (Susceptible), инфицированных (Infectious) и переболевших, приобретших иммунитет (Recovered).
Сразу можно сказать, что для гриппа остановка на Recovered не всегда работает. Допустим, человек вылечился, приобрел антитела и, уверенный в своей неуязвимости, поехал в офис на метро. Через два дня снова лежит дома в постели с температурой, головной болью и прочими признаками гриппа. Почему? Потому что на территории циркулируют два разных штамма, отличающиеся комбинацией гемагглютинина и нейраминидазы. И один их них иммунная система вовремя не распознала. Плюс организм ослаб после борьбы с предыдущим штаммом — возможно, это обстоятельство приведет к более тяжелому течению болезни, вызову скорой помощи и госпитализации.
Модель SIR описывается системой из трех дифференциальных уравнений:

С точки зрения математики то, что подкрашено красным, означает, что мы имеем дело с нелинейностью. Мы не сможем найти решение аналитически, составляя формулы через известные нам функции. Приходится применять численное решение. Коэффициенты, которые здесь фигурируют, определяют скорость перехода из одной группы в другую: β — скорость перехода из здоровых в заболевшие, γ — из заболевших в выздоровевшие.
В конечном итоге мы получим тождество:

S(0) — количество людей, которые могут заболеть до начала эпидемии. И это же индекс репродукции R0, хорошо известный всем, кто следил за развитием пандемии COVID-19. Он означает, сколько человек может заразить один заболевший. При R0 больше единицы развивается эпидемия. Если индекс меньше единицы, эпидемия затухает.
SIR-модель подразумевает, что люди составляют непрерывную, однородную среду. Как газ или жидкость. Популяция считается постоянной, не учитывается убыль населения — естественная или от вируса — и прибыль. На практике это приводит к серьезной погрешности в расчетах.
Помните пример с гриппом в закрытой школе для мальчиков? Даже если с помощью математики смоделировать ситуацию в школе с доверительным интервалом (95 %), получится, что переболели примерно 750 учеников. Но мы точно знаем, что заболевших было 512. R0 примерно равен 16, а на самом деле был 1,69. Если бы мы так же в лоб моделировали ситуацию не для одной школы, а, скажем, для города или страны, наши прогнозы вызвали бы тысячи вопросов. Как же быть?
Важно понимать, что грипп не развивается молниеносно. Есть латентный период и инкубационный период. От начала заражения до появления клинических симптомов — в среднем 2 дня (у COVID-19, как вы знаете, до 14 дней). При этом инкубационный период частично пересекается с периодом инфицирования: больной еще не знает, что болен, но уже заражает окружающих.

Для учета зараженных в инкубационном периоде в SIR-модель вводят группу E (Exposed). Модифицированная модель SEIR — это новая система уравнений, новый коэффициент, но R0 по-прежнему получается 16.

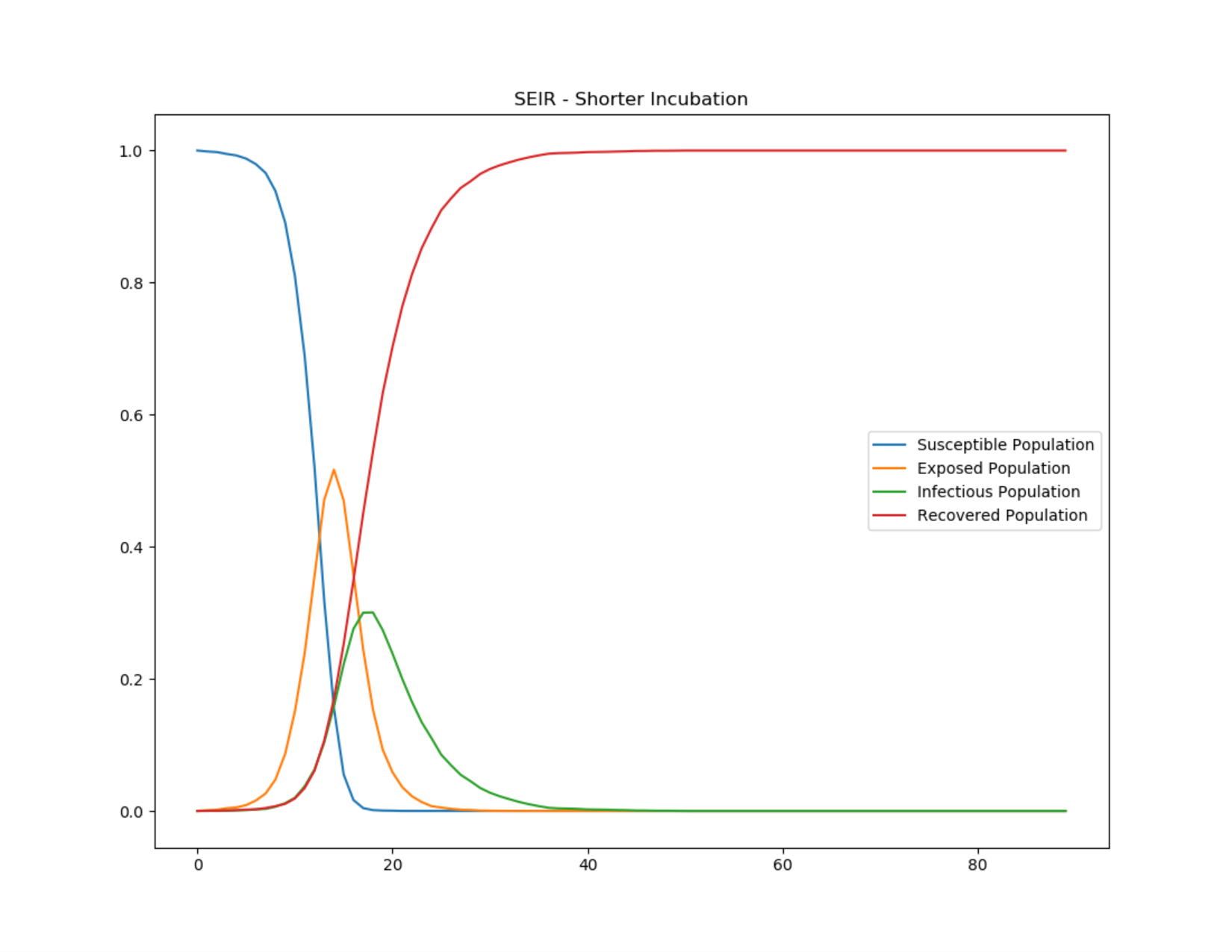
Можно еще учитывать тех, кто находится на карантине, и построить модель SEIQR, где Q значит «карантин». Но и тогда получим R0, равный 6–8, что по-прежнему далеко от реального 1,69.
Подобных вариаций SIR-модели много. Если, например, принимать в расчет количество умерших, но без карантина, получим модель SEIRD и т. д. Однако что бы мы ни предпринимали, SIR-моделирование не дает приемлемой точности. Дело в том, что любая модификация модели является детерменистской: для нее не существует случайных причин. Грипп же предполагает массу случайностей на каждом этапе, от прикрепления вируса к клетке до прохождения многочисленных ловушек иммунитета. Закрепиться в нашем организме — квест для каждого вириона.
Модели, которые учитывают случайности
Если количество уязвимых к инфекции и заболевших — случайные величины, модель называют стохастической. Она пытается ответить на вопрос: если на k-неделе x — это количество здоровых, то какая вероятность, что на неделе k+1 х будет означать количество заболевших? И кроме того — какая вероятность избежать инфекции (u)?
Когда u зависит от числа заболевших (в том смысле, что чем больше заболевших, тем меньше вероятность избежать заболевания), мы получаем модель Рида-Фроста. Если же предполагаем, что вероятность заболеть не зависит от количества заболевших, получаем модель Гринвуда.

Это уже более гибкие модели, не непрерывные — их еще называют ветвящимися (branching model). Число выздоровевших убывает, вероятность заболеть в ближайшую неделю меняется в зависимости от ситуации на предыдущей неделе. Стохастические модели получили широкое распространение в 1970-е, постоянно развивались и сейчас в целом имеют неплохое согласие с наблюдениями различных инфекций.
Что еще можно учесть? Например, то, что люди по-разному социализированы. Кто-то пять дней в неделю общается с десятками коллег и постоянно встречается с друзьями, у кого-то друзей нет и работа из дома. Существует вероятность, что у них разные шансы заболеть гриппом, поэтому можно рассматривать распространение инфекции на социальном графе. Выглядит он примерно так:

С таким моделированием тоже есть проблемы, потому что на практике невозможно построить граф, фиксируя все социальные контакты.
Еще одна сложность для моделирования — достоверность данных. Мы строим прогнозы на основе наблюдений: столько-то человек за такой-то период заболели, надо это учесть. Но что значит «заболели»? Пациент с симптомами гриппа должен прийти к врачу, а врач должен передать информацию в надзорные органы: температура выше 38 градусов, кашель, симптомы появились в течение 10 дней. Это называется гриппоподобным заболеванием (ILI, Influenza-like illness).
Чтобы выявить случаи «чистого гриппа», используют термин ILI+, подразумевающий, что для диагноза нужен тест, который в мазке из носоглотки выявит гемагглютинин, нейраминидазу или РНК гриппа. Затем определяют долю тест-позитивных среди всех обратившихся с симптомами гриппа. Очевидно, эти данные позволяют строить более точные модели.
Что еще нужно учитывать?
Вернемся к процессу заражения. При дыхании, чихании и кашле инфицированного в воздух попадают частицы, которые делят по размеру: больше 5 микрометров (Droplet, капля) и меньше 5 микрометров (Airborne, зародыш капли). Если кашель генерирует примерно 10 тысяч частиц, чихание — миллион. Поэтому следует сторониться прежде всего тех, кто чихает.
Частиц меньше 5 микрометров большинство. Они почти беспрепятственно проходят через верхние дыхательные пути и попадают в легкие. Там уже нет ресничкового эпителия, густо покрытого слизью, который служил серьезным барьером для частиц побольше. Зато есть альвеолярные макрофаги нейтрофилы, готовые атаковать любой патоген, правда, не всегда эффективно. Зародыши капли легко переносятся по воздуху и долго оседают, в 4 раза медленнее частиц размером 10 микрометров.
Серьезное значение для распространения вируса имеет скорость испарения частиц. Чтобы испариться наполовину, нужно от 0,01 до 10 секунд. Разница напрямую связана с влажностью: чем ниже влажность, тем быстрее испаряется частица. Больной в лифте чихнул, влажность низкая — частица, не успев осесть, испарилась до размера зародыша и продолжает парить в воздухе, пока не попадет в нос здоровому человеку.
Теперь вспомним, когда влажность в помещениях минимальна. В Германии, например, в феврале и декабре — на пике отопительного сезона. Вот почему у гриппа выраженная сезонность (у туберкулеза, скажем, такой сезонности нет). Таким образом, знание динамики аэрозольных частиц позволяет объяснить, почему эпидемии возникают в определенное время года. Во-вторых, помогает оценить риск заражения.
Вместо заключения
Мы многое знаем о гриппе, даже можем посчитать, как «зараженные» частицы летают в воздухе и как испаряются. Но мы также знаем, что эти процессы носят вероятностный характер. Все их учесть невозможно даже с помощью совершенных математических методов или машинного обучения. Фактически, мы не моделируем эпидемии, а строим предсказания. Целую серию предсказаний: для наступления эпидемии, для пика, для интенсивности. И чем дальше от пика, тем меньше точность: в пределах одной недели точность 75 %, в пределах двух недель она падает до 25 %.
Такие предсказания, несмотря на все погрешности, необходимы. С помощью SIR-модели можно определить, например, что эпидемия начнется в первой декаде декабря, продлится три недели, заболеет 1 миллион человек, в пике будет 100 тысяч случаев инфицирования. Это позволит системе здравоохранения подготовиться, приготовить нужное количество лекарств и мест в больницах. Затем имеет смысл применять вероятностные модели, уточняя прогнозы: учитывать вакцинированных, вероятность заразиться каждой группе в популяции и т. д. Пока что это оптимальная практика, помогающая справляться с эпидемиями вирусов, которые мы неплохо знаем.
Чтобы понять, какой лучший способ справиться с эпидемий, достаточно посмотреть на этот график:

Сверху — количество зарегистрированных случаев гриппа в популяции, снизу — с учетом вакцинации.
Мораль простая: полезно мыть руки, проветривать помещения, включать увлажнитель, но без вакцинации победить эпидемию гриппа нельзя. И неважно, какую модель использовать для предсказаний.
Если вам интересно, как математика и машинное обучение помогают бороться с фейковыми новостями, слухами и теориями заговора во время эпидемий, рекомендуем доклад Преслава Накова на бесплатной онлайн-конференции IT NonStop (18–20 ноября 2021). Преслав Наков — главный научный сотрудник Катарского исследовательского института вычислительной техники, HBKU. Он возглавляет мегапроект Tanbih, разработанный в сотрудничестве с MIT, с помощью которого, в частности, выявляют фейки о COVID-19.
Всего в программе конференции — более 40 докладов и воркшопов специалистов из Microsoft, AWS, Ocado, Codete, Ciklum, Eleks, SoftServe, Toloka, Yandex, DataArt и других компаний.
Комментарии (3)

belch84
01.10.2021 15:45Не думаю, что SEIR модели совсем уж бесполезны и представляют только теоретический интерес, и не уверен, что они совсем уж не учитывают элементы случайности. Поведение такой модели описывается множеством параметров (вроде скорости заражения, длительности заразного периода и т.д), которые заранее, конечно, не известны. Параметры можно подобрать на основе статистических данных, но этих данных будет достаточно, когда эпидемия уже разгорелась. Кроме того, в простейшем случае эти параметры предполагаются постоянными, но на самом деле они, конечно же, зависят от времени. Такая модель не может предсказать начало эпидемии или, например, наступление второй волны, но может дать краткосрочный прогноз. После накопления статистики модель нужно будет перестраивать, находя новые значения параметров, и так до конца эпидемии. Вот пример модели SEIRQD с изменяющимся параметром «скорость заражения», для простоты считается что эта скорость изменяется (увеличивается) скачком на 315-ый день эпидемии, при достаточной величине скачка возникает вторая волна.
SEIRQD-модель эпидемии с образованием второй волны

omxela
01.10.2021 23:22По сравнению, скажем, с https://habr.com/ru/post/575596/ звучит как-то простовато. Кривая с максимумом - это здорово, но это работает на коротких отрезках времени. Дело не в том, что не учли то-то и то-то - всего не учтёшь. Дело в том, что даже если учтёшь, то в подобного рода некорректно поставленных задачах трудности чисто математического свойства. Чем больше отрезок времени - тем более непредсказуем результат. Точно так же, как с погодой.



Pochemuk
Что все эти модели не учитывают, так это кластеризацию общества. И эта тема почти нигде не рассматривается (Встречал одну статью, но кроме указания на проблему ничего конкретного предложено не было. Встречал еще одну статью, в которой доказывалось, что в условиях ограниченного числа знакомств рост с экспотенционального быстро становится константой, и это наглядный пример, но слишком упрощенный).
У политической элиты — один круг общения, у деловой — другой, но сильно пересекающийся с первым. У творческой богемы — третий. У работников сферы обслуживания, офисных работников, работников физического труда, самозанятых — четвертый, пятый, шестой, седьмой, слабо касающиеся первых трех, но контактирующие между собой.
Даже в пределах одной конторы работники разных отделов могут контактировать друг с другом в основном через начальство.
Все это приводит к тому, что болезнь развивается внутри кластера по логистическому закону, но быстро выдыхается. А вот распространение между кластерами уже линейно, т.к. точек контактов между кластерами на порядки меньше, чем суммарно внутри них.
Для наглядности представим круг. Длина его периметра (число людей контактирующих с внешним миров в каждый момент времени) пропорционально радиусу. А вот площадь (число людей, контактирующих между собой в этом кластере) — квадрату радиуса. А если учесть, что заболевший может уйти на больничный и снизит число контактов на границе круга, то скорость распространения между кластерами подчиняется совсем другим законам, чем SIR/SEIQR и прочим.
И все эти SIR-модели идут лесом, т.к. базируются на однородности среды и на допущении, что каждый человек может заразить каждого. Но вот я, например, вряд ли напрямую заражу Монику Белуччи. И даже ее повара.