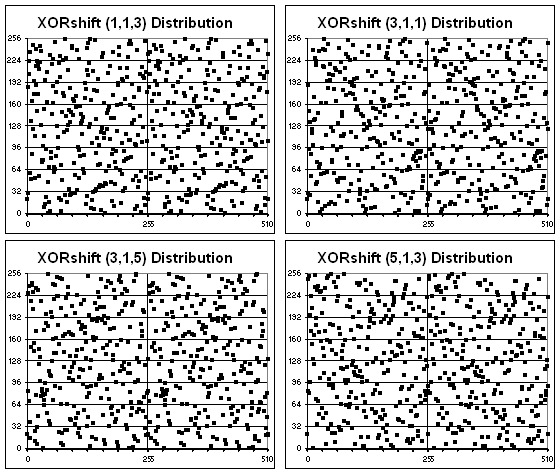
Выдача XORShift кажется случайной

Исследователь Мостафа Хассан (Mostafa Hassan) сумел взломать два генератора псведослучайных чисел (ГПСЧ) с помощью машинного обучения. Обученная двуслойная нейросеть предсказала выдачу генератора xorshift128 с точностью 100%.

Во второй части своей работы Мостафа описал ещё одну нейросеть, которая взломала популярный генератор Mersenne Twister (вихрь Мерсенна, MT, MT19937) тоже с точностью 100%.

Взлом xorshift128

Генераторы типа XORShift являются одними из самых быстрых криптографически нестойких генераторов случайных чисел, а их реализация не предполагает больших объёмов кода, поэтому они часто используются в программном обеспечении. Иногда их ошибочно используют вместо криптографически стойких ГПСЧ.

Как работает xorshift128? Код реализации алгоритма можно найти на Википедии и в репозитории на Github:

def xorshift128():
    '''xorshift
    https://ja.wikipedia.org/wiki/Xorshift
    '''

    x = 123456789
    y = 362436069
    z = 521288629
    w = 88675123

    def _random():
        nonlocal x, y, z, w
        t = x ^ ((x << 11) & 0xFFFFFFFF)  # 32bit
        x, y, z = y, z, w
        w = (w ^ (w >> 19)) ^ (t ^ (t >> 8))
        return w

    return _random

Именно эта функция использовалась в модели машинного обучения (ML).

Как видим из кода, реализация довольно простая. У неё четыре внутренних числа, x, y, z и w, которые одновременно представляют сид и состояние ГПСЧ. Конечно, можно изменить этот код, чтобы вместо жесткого кодирования сида использовать какой-нибудь вызов функции. Каждый раз, когда мы вызываем генератор, он будет сдвигать внутренние переменные следующим образом: y -> x, z -> y и w -> z. Новое значение w оценивается путём применения некоторых битовых манипуляций (сдвигов и XOR) к старым значениям x и w. Новое значение w затем возвращается как новое случайное число на выходе генератора случайных чисел.

На схеме ниже О₀, О₁, О₂ и так далее — это результат вычислений с вышеупомянутыми переменными:

O0 = W0 ^ W19 ^ X0 ^ X8
O1 = W1 ^ W20 ^ X1 ^ X9
.
.
O31 = W31 ^ X20 ^ X31

Получается такая схема:



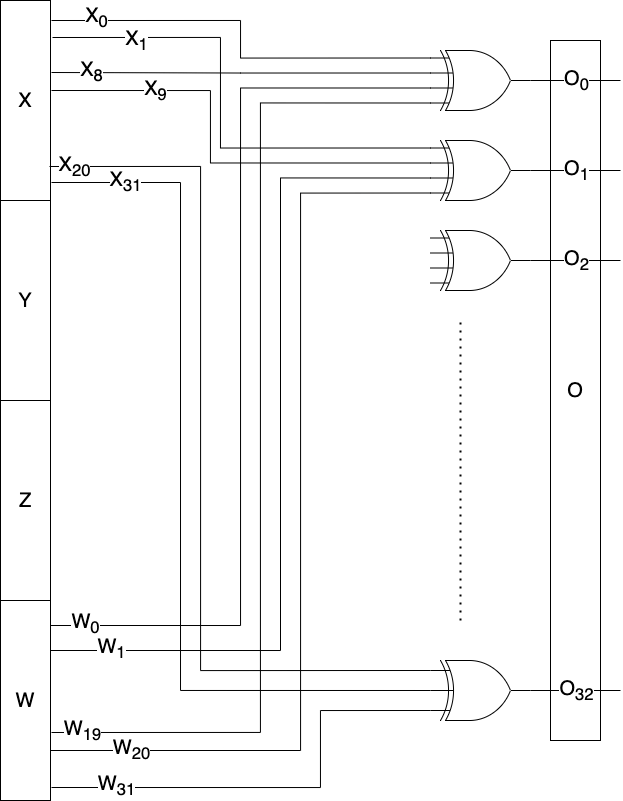
Как видим, значение O вычисляется на основе только двух чисел x и w (конечно, значения y и z тоже предварительно используются).

На первый взгляд кажется контринтуитивным обучать нейросеть на массиве псевдослучайных чисел, в которых по определению не должно быть никаких закономерностей. В то же время любая ML-модель обучается именно на паттернах данных. Таким образом, как будто нет смысла обучать её на ГПСЧ, которые не должны следовать паттернам. И не только обучаться, но и получить точность 100%.

Но это всё-таки возможно. Слабость простейших генераторов типа XORShift состоит в том, что каждое новое псевдослучайное число зависит от четырёх предыдущих чисел, как показано выше. Это и позволяет нейросети предсказывать результат, даже не зная начального значения (сида), с которого начинают генерироваться числа.


В качестве иллюстрации «предсказуемых» ГПСЧ — метод средних квадратов, этот алгоритм Джон фон Нейман представил на конференции по прикладной математике в 1949 году

Как машинное обучение может взломать ГПСЧ? По сути, в данном случае разработчик закодировал бинарную схему xorshift128 в виде нейронной сети. Тот факт, что вы можете кодировать произвольные двоичные цепи в виде нейронных сетей, хорошо известен.


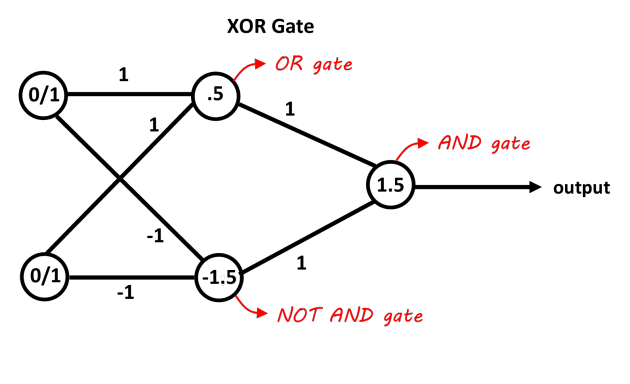
Представление функции XOR с двумя входами в двуслойной нейросети

Интересным и неожиданным результатом исследования является демонстрация, что можно обучить эту сеть, используя стандартные градиентные методы, если подобрать подходящую функцию потерь, хорошо понимать решаемую задачу (то есть отлично понимать криптографию) — и спроектировать сеть с пониманием алгоритма, который она должна моделировать. Другими словами, это можно рассматривать в качестве примера, что грамотное проектирование сети и выбор функции потерь существенно влияет на производительность нестандартной ML-модели.

Код для обучения и тестирования нейросети, взломавшей xorshift128, опубликован здесь.

Чтобы результаты xorshift128 стали менее предсказуемы или вообще непредсказуемы для нейросети, рекомендуется добавить в сид алгоритма ещё одну переменную, которая будет решать:

1. Какие переменные выбрать из x, y, z и w для генерации o.
   
2. На сколько бит сдвинуть каждую из переменных.
   
3. В каком направлении сдвигать переменные — влево или вправо.

Взлом вихря Мерсенна

Схожий подход автор использовал для взлома Mersenne Twister (MT, вихрь Мерсенна), одного из самых популярных генераторов псевдослучайных чисел, который считался относительно надёжным. Вихрь Мерсенна основыван на свойствах простых чисел Мерсенна (отсюда название) и обеспечивает быструю генерацию высококачественных псевдослучайных чисел. Он лишён многих недостатков, присущих другим ГПСЧ, таких как малый период, предсказуемость, легко выявляемые статистические закономерности.

Тем не менее, этот генератор не является криптостойким, что и доказал во второй части своего исследования Мостафа Хассан.

Есть много вариантов MT, самый популярный MT19937, период которого составляет 2¹⁹⁹³⁷? 1 (приблизительно 4,3x10⁶⁰⁰¹).

MT можно рассматривать как нестандартную форму регистра сдвига с линейной обратной связью (LFSR). Идея LFSR заключается в использовании линейной булевой функции, такой как XOR, со старым значением регистра для получения нового значения регистра. В МТ внутреннее состояние сохраняется в виде последовательности 32-битных слов. Размер внутреннего состояния зависит от варианта МТ, в случае MT19937 он равен 624. Псевдокод МТ приведён ниже, из Википедии:

 // Create a length n array to store the state of the generator
 int[0..n-1] MT
 int index := n+1
 const int lower_mask = (1 << r) - 1 // That is, the binary number of r 1's
 const int upper_mask = lowest w bits of (not lower_mask)
 
 // Initialize the generator from a seed
 function seed_mt(int seed) {
     index := n
     MT[0] := seed
     for i from 1 to (n - 1) { // loop over each element
         MT[i] := lowest w bits of (f * (MT[i-1] xor (MT[i-1] >> (w-2))) + i)
     }
 }
 
 // Extract a tempered value based on MT[index]
 // calling twist() every n numbers
 function extract_number() {
     if index >= n {
         if index > n {
           error "Generator was never seeded"
           // Alternatively, seed with constant value; 5489 is used in reference C code[53]
         }
         twist()
     }
 
     int y := MT[index]
     y := y xor ((y >> u) and d)
     y := y xor ((y << s) and b)
     y := y xor ((y << t) and c)
     y := y xor (y >> l)
 
     index := index + 1
     return lowest w bits of (y)
 }
 
 // Generate the next n values from the series x_i 
 function twist() {
     for i from 0 to (n-1) {
         int x := (MT[i] and upper_mask)
                   + (MT[(i+1) mod n] and lower_mask)
         int xA := x >> 1
         if (x mod 2) != 0 { // lowest bit of x is 1
             xA := xA xor a
         }
         MT[i] := MT[(i + m) mod n] xor xA
     }
     index := 0
 } 

Обратите внимание, что в коде 13 констант w, n, m, r, a, u, d, s, b, t, c, l, f — они могут изменяться в разных версиях алгоритма.

Из псевдокода также видно, что алгоритм разбивается на два основных шага: 1) смена числа; 2) трансформация числа, чтобы превратить его в «случайное». Первый шаг выполняется 1 раз каждые 624 вызова (в MT19937), то есть исходное число периодически меняется. Второй шаг выполняется 624 раза, то есть из каждого исходного числа получается 624 «случайных» результата.

В данном случае автору пришлось обучать две модели ML для двух этапов работы алгоритма. Затем он использовал их вместе, чтобы распознать исходное число по его результату (реверс).

Первая модель

Например, для первого этапа в вышеприведённом коде действует такая схема:

MT[i] = f(MT[i - 624], MT[i - 624 + 1], MT[i - 624 + m])

= f(MT[i - 624], MT[i - 623], MT[i - 227]) (при m = 397, как в MT19937)

Каждое следующее состояние числа зависит от трёх предыдущих состояний. Если конкретно, для генерации нового числа из трёх существующих можно использовать такой код C++, он выдаёт тот же результат, что в реальных ГПСЧ, которые используются на практике:

uint inp_out_xor_bitsY[32] = {
    0xfe87caa8,
    0x400091,
    0x84092000,
    0x1000044,
    0x2040489,
    0x6000990,
    0x8001220,
    0xeea7cea0,
    0x20004880,
    0x4080002,
    0x80002200,
    0xff95eeac,
    0x2000880,
    0x8081202,
    0x10102404,
    0x204008,
    0x44089102,
    0x84892122,
    0xff85cae8,
    0x2440010,
    0x84012002,
    0x1100040,
    0xecb3ea6d,
    0x6400980,
    0xc881302,
    0x6fa7eee0,
    0x22004800,
    0x80102,
    0x88002000,
    0xef95eaac,
    0x22000080,
    0xc001300
};

uint gen_new_number(uint MT_624, uint MT_623, uint MT_227) {
    uint r = 0;
    uint i = 0;
    do {
        r ^= (MT_623 & 1) * inp_out_xor_bitsY[i++];
    }
    while (MT_623 >>= 1);
    
    MT_624 &= 0x89130204;
    MT_624 ^= MT_624 >> 16;
    MT_624 ^= MT_624 >> 8;
    MT_624 ^= MT_624 >> 4;
    MT_624 ^= MT_624 >> 2;
    MT_624 ^= MT_624 >> 1;
    r ^= (MT_624 & 1) * 0x44081102;
    
    r ^= MT_227;
    return r;
}

Вторая модель

Вторая нейросеть для трансформации оказалась гораздо сложнее: 672 нейрона вместо 128, 41 632 обучаемых параметра вместо 9440. В остальном две модели похожи: тип Dense (плотная свёрточная сеть), функция потерь binary_crossentropy, скрытый слой relu, внешний слой sigmoid.

После обучения модель показала битовую точность 100% как на наборе тренировочных данных, так и на тестовом наборе. Для проверки на стороннем ГПСЧ было дополнительно сгенерировано 100 000 случайных чисел с новыми сидами — и тестирование на этом полностью новом наборе данных тоже показало точность 100%.

То есть модель способна по результату MT19937 точно распознать сид, а уже из него получить все 624 «случайных» числа.

Исходный код в репозитории.

---

Вывод из этого такой: хотя результат ГПСЧ кажется случайным для человека (см. КДПВ), обученная нейросеть может найти взаимосвязь между входящими и исходящими числами — и предсказать результат.

Нужно заметить, что небезопасные ГПСЧ используются как часть реальных криптографически безопасных ГПСЧ. Например, вихрь Мерсенна используется в алгоритме CryptMT.

---