Детерминированный факторный анализ - это метод исследования влияния факторов на результативный показатель.

Предполагается, что связь факторов с результативным показателем носит функциональный характер, которая  выражена математической формулой.

Например, выручку логистической компании можно представить так:

Это мультипликативный вариант модели.

Мы хотим проследить изменение выручки за период: за счет чего изменилась выручка в рублях в отчетном месяце по отношению к предыдущему. Для этого будем использовать интегральный способ.

В отчетном месяце:
[B] выручка - 250 руб, [????₁] цена - 50 руб/шт, [????₁] объем - 5 шт;
в предыдущем месяце:
[A] выручка - 120 руб, [????₀] цена - 40 руб/шт, [????₀] объем - 3 шт.

Данное изменение можно изобразить прямоугольником:

????₀=????₀∙????₀,
????₁=(????₁−????₀)∙????₀,
????₂=????₀∙(????₁−????₀),
????₃=(????₁−????₀)∙(????₁−????₀),
????₄=????₀+????₁+????₂+????₃=????₁∙????₁

Изменение выручки:
????₄ - ????₀ = ????₁+????₂+????₃
Изменение выручки за счет цены:
????₁+????₃/2
Изменение выручки за счет объема:
????₂+????₃/2

Изменение выручки: (250 - 120) = 130
Изменение выручки за счет цены: (50 - 40) * 3 + [(50 - 40) * (5 - 3)]/2 = 30 + [10 * 2]/2 = 40
Изменение выручки за счет объема: 40 * (5 - 3) + [(50 - 40) * (5 - 3)]/2 = 80 + [10 * 2]/2 = 90
Проверим: 130 = 40 + 90 (верно).

Выручка в предыдущем месяце составляла 120 руб. Уменьшение цены на 10 руб/шт увеличило выручку на 40 рублей, при этом увеличение объема на 2 шт. увеличило выручку на 90 руб. Выручка в текущем месяце – 250 руб.

Для двумерного случая можно использовать данные формулы, но с увеличением размерности модели, подобрать формулы становится проблематично. Автоматизируем данный процесс.

Допустим, что наша модель усложнилась и теперь:

В отчетном месяце:
[B] выручка - 250 руб, [????₁] цена - 5 руб/кг, [????₁] объем - 5 шт, [????₁] вес - 10 кг/шт;
в предыдущем месяце:
[A] выручка - 96 руб, [????₀] цена - 4 руб/шт, [????₀] объем - 3 шт [????₂] вес - 8 кг/шт.

Так как система имеет два состояния A и B, то фигуру необходимо разбить на 2^???? частей, где ???? – количество измерений.
Так для 3 измерений необходимо 2³ = 8 частей.

Изменение выручки за счет цены-и-объема необходимо поделить пополам,
также необходимо поделить пополам изменение выручки за счет цены-и-веса и веса-и-объема.

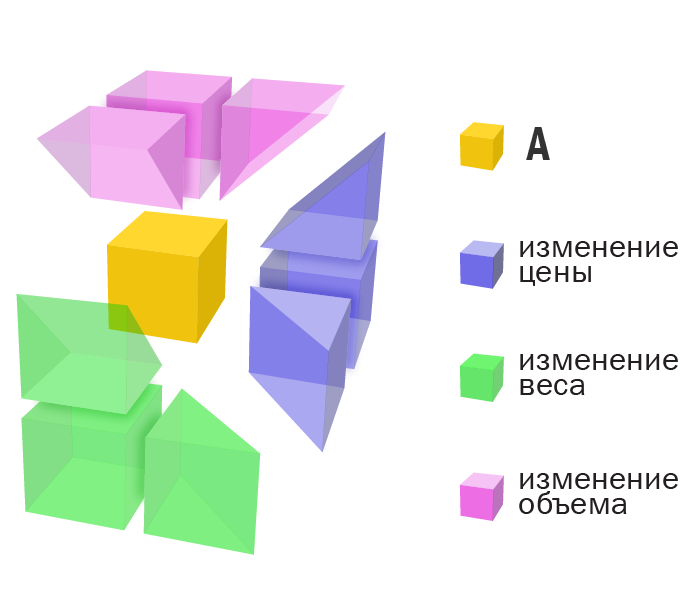
Изменение выручки за счет цены-веса-и-объема необходимо разделить на 3 части:

Составим таблицу, ???? - цена, ???? - вес, ???? - объем:

Где Δ????=(????1−????0),
Δ????=(????1−????0),
Δ????=(????1−????0),
1 – наличие Δ.
Дельта (Δ) показывает за счет какого фактора происходит изменение.

Кол-во Δ в строке показывает на сколько частей необходимо делить фигуру, для этого необходимо вывести дополнительный столбец с количеством Δ (????Δ).

Суммы по столбцу ????????, ????????, ???????? – это значение влияния фактора.
В итоге: A → ????₀+????????+????????+???????? = B

Для нашего примера:
Выручка в предыдущем месяце составляла 120 руб. Увеличение цены на 1 руб/кг увеличило выручку на 36,3 руб, при этом увеличение веса на 2 кг/шт. увеличило выручку на 36,3 руб., также увеличение объема на 2 шт. увеличило выручку на 81,3 руб. Выручка в текущем месяце – 250 руб.

Теперь код:

import numpy as np

from typing import *
from itertools import *


def factors_product(beg: List, end: List) -> List:

    beg = np.array(beg)
    end = np.array(end)
    # (1) генерируем матрицу наличия Δ, (0, 0, 0) нам не нужна
    sep = np.array(list(product([0, 1], repeat=len(beg))))[1:]
    # (2) рассчитываем матрицу отклонений факторов + матрица начальных значений
    delta = sep * (end-beg) + beg * (1-sep)
    # (3) найдем ????Δ
    k = sep.sum(1)
    # (4) найдем произведение состояния факторов / ????Δ
    m = (sep * (end-beg) + beg * (1-sep)).prod(1) / k
    # (4) поместим m на соответствующие факторы и посчитаем суммы влияния
    result = (sep.T * m).sum(1)
    return result

Или return в одну строку:

def factors_product(beg: List, end: List) -> List:

    beg = np.array(beg)
    end = np.array(end)
    sep = np.array(list(product([0, 1], repeat=len(beg))))[1:]

    return (sep.T*((sep*(end-beg)+beg*(1-sep)).prod(1)/sep.sum(1))).sum(1)

# проверим нашу задачу
!pip install detfa

from detfa import factors_product

print(factors_product([4,3,8], [5,5,10]))
>> [36.33333333 81.33333333 36.33333333]