Стандартная гауссова статистика работает на основе следующих предположений. Центральная предельная теорема утверждает, что при увеличении числа испытаний, предельное распределение случайной системы будет нормальным распределением. События должны быть независимыми и идентично распределены (т.е. не должны влиять друг на друга и должны иметь одинаковую вероятность наступления). При исследовании крупных комплексных систем обычно предполагают гипотезу о нормальности системы, чтобы далее мог быть применен стандартный статистический анализ.

Часто на практике изучаемые системы (от солнечных пятен, среднегодовых значений выпадения осадков и до финансовых рынков, временных рядов экономических показателей) не являются нормально-распределенными или близкими к ней. Для анализа таких систем Херстом [1] был предложен метод Нормированного размаха (RS-анализ). Главным образом данный метод позволяет различить случайный и фрактальный временные ряды, а также делать выводы о наличии непериодических циклов, долговременной памяти и т.д.

Алгоритм RS-анализа

1. Дан исходный ряд 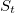. Рассчитаем логарифмические отношения:
   
   
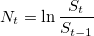
2. Разделим ряд на смежных периодов длиной . Отметим каждый период как 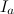, где 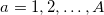. Определим для каждого 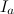среднее значение:
   
   
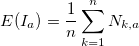
3. Рассчитаем отклонения от среднего значения для каждого периода :
   
   
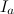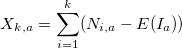
4. Рассчитаем размах в пределах каждого периода:
   
   
   
5. Рассчитаем стандартное отклонения для каждого периода :
   
   
   
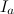6. Каждый 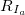делим на . Далее рассчитываем среднее значение R/S:
   
   
   
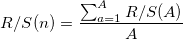
7. Увеличиваем и повторяем шаги 2-6 до тех пор, пока
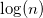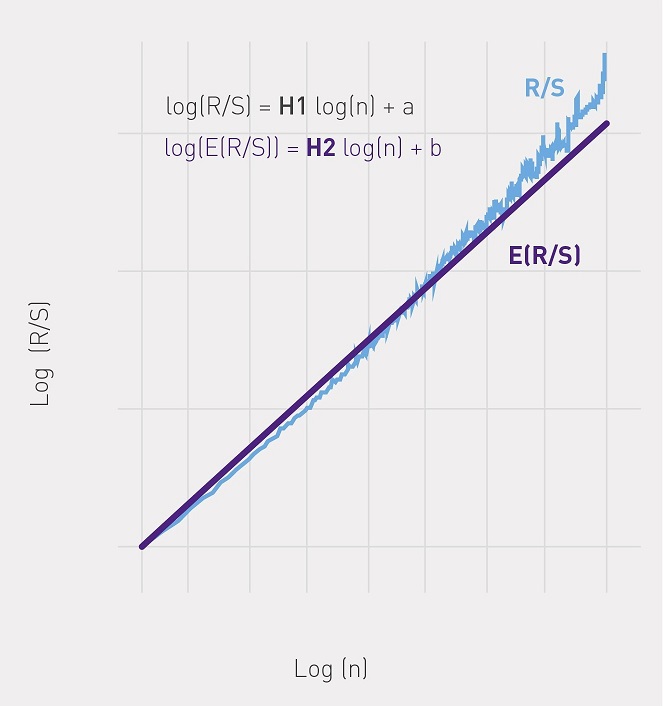
8. Строим график зависимости от и с помощью МНК находим регрессию вида: 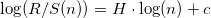, где H – показатель Херста (см. рисунок).

Проверка значимости

Далее проверяем полученный результат на значимость. Для этого проверяем гипотезу о том, что анализируемая структура является нормально-распределенной. R/S являются случайными переменными, нормально распределенными, тогда можно предположить, что H также распределены нормально. Асимптотическим пределом для независимого процесса является показатель Херста равный 0.5. Энис и Ллойд [2], а также Петерс [3] предложили использовать следующие ожидаемые показатели R/S:

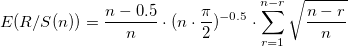
Для n наблюдений находим ожидаемый показатель Херста: .



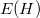Ожидаемая дисперсия будет следующей: , где T — количество наблюдений в выборке.

Выборочная статистика: .
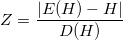Сравниваем ее с критическим значением нормированного нормального распределения.

Если выборочное значение меньше критического, то гипотезу о нормальном распределении системы не отвергаем на данном уровне значимости. Структура случайна и имеет нормальный закон распределения.

Список литературы:

1. Херст, Г. Э., 1951. «Долгосрочная вместимость водохранилищ». Труды Американского общества гражданских инженеров, 116, 770-808.
2. Anis, A.A., Lloyd, E.H. (1976) The expected value of the adjusted rescaled Hurst range of independent normal summands. Biometrica 63: 283-298.
3. Peters, E.E. (1994) Fractal Market Analysis. Wiley, New York. ISBN 0-471-58524-6.