Излучение спутникового радара проходит сквозь облака и позволяет получать снимки в темноте, в дождь и снег, когда оптическая съемка невозможна. При этом, накапливающаяся при прохождении излучения через атмосферные неоднородности временная задержка при обработке данных спутниковой радарной съемки трансформируется в ложные смещения поверхности. Такая задержка не влияет на значение когерентности (вычисляемое в так называемом окне, сильно меньшем характерного масштаба атмосферной помехи), что не позволяет обнаружить и исключить такие помехи непосредственно в процессе построения интерферограмм. Получается, что радарные снимки сделать можно в любое время и при любой погоде, вот только многие снимки оказываются искаженными, порой до неузнаваемости всей площади съемки, и стандартными методами оценки когерентности интерферограмм мы об этом даже не узнаем. Обсуждаемая проблема имеет различные решения, некоторые из которых мы и рассмотрим с примерами Jupyter ноутбуков Live Example S1A_Stack_CPGF_T173 on Google Colab и Live Example S1A_Stack_CPGF_T173 Plus on Google Colab.
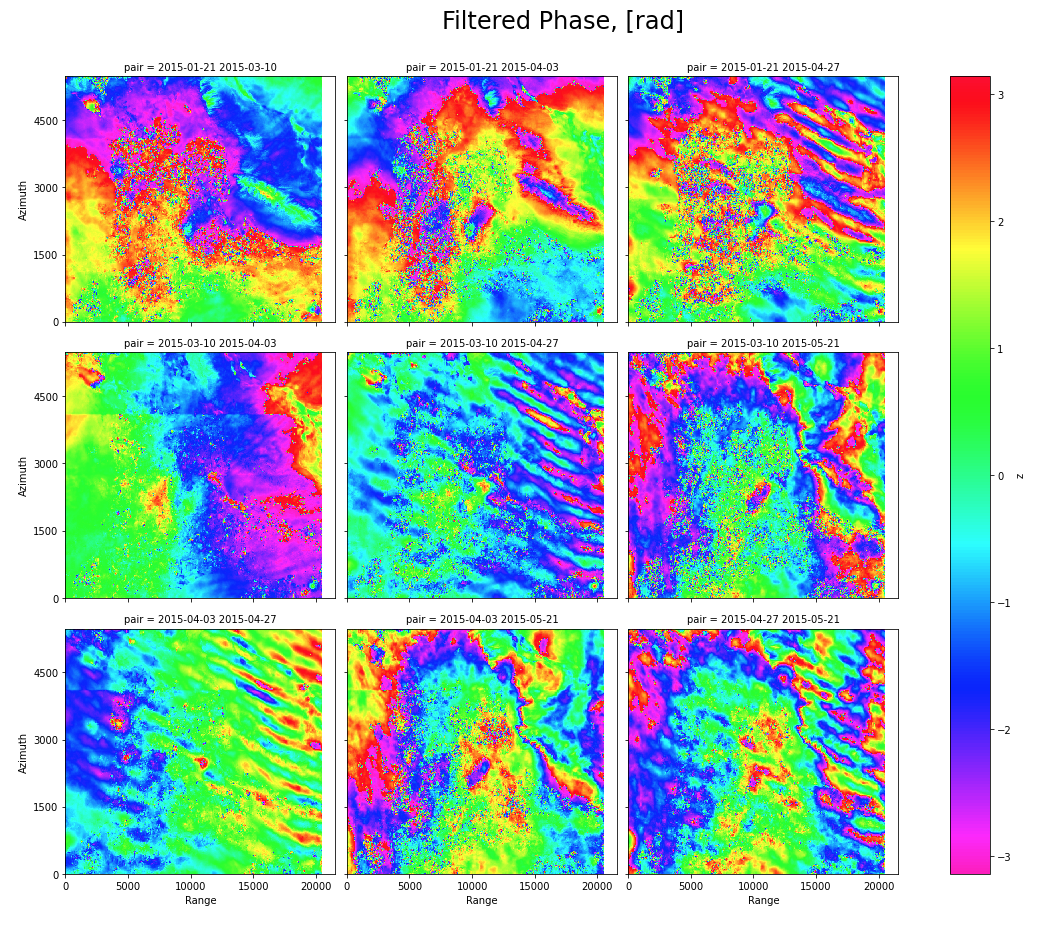
Интерферограмма в центре особенно явно зашумлена атмосферной помехой, если присмотреться, то эта же помеха заметна на всех интерферограммах, включающих снимок 2015-04-27. Удаление этого одного снимка позволит полностью избавить всю серию интерферограмм от заметных атмосферных помех.
Введение
Для общеизвестной проблемы существуют и известные ее решения. Есть различные способы, от ручного удаления снимков с явно видимыми атмосферными задержками до итеративного анализа серии снимков для вычисления атмосферных эффектов в предположении медленных линейных смещений поверхности и до полного игнорирования атмосферных эффектов. Первый способ трудоемок, зато может использоваться как сам по себе, так и в комбинации с другими методами. Второй подход работает только в предположении о медленном и равномерном движении поверхности, что зачастую явно не выполняется. Последний метод, пожалуй, наиболее распространен и не зря — если нас интересует только долгосрочный линейный тренд движения исследуемой территории, при его вычислении атмосферные эффекты взаимно компенсируются. Действительно, при построении серий интерферограмм за сколь угодно большой период времени, на каждую интерферограмму влияют атмосферные помехи только выбранной пары снимков, причем помеха первого снимка вычитается из помехи второго — то есть эта помеха не накапливается при анализе больших серий изображений (не кумулятивна).
Итак, во многих случаях мы можем воспользоваться известными методами, и в то же время все они не пригодны для автоматизированного анализа территории со сложным движением поверхности. Вышеназванные методы обладают одним общим свойством — они никак не учитывают физические свойства атмосферы, а пытаются использовать или визуальную оценку, или некоторые предположения о получаемых результатах. В то же время, свойства атмосферы достаточно изучены для того, чтобы воспользоваться этими знаниями для поиска атмосферных помех на радарных изображениях. Далее мы рассмотрим подробнее именно те методы, которые опираются на характеристики атмосферы.
На примере SBAS диаграммы ниже показаны анализируемые пары снимков (9 пар):
Посмотрим, что получится, если использовать интерферограммы "как есть" без корректировки атмосферных помех для вычисления годовой скорости смещения каждого пиксела территории. Для оценки результатов достаточно построить линейный тренд годового движения каждого пиксела территории (в данном случае, методом наименьших квадратов), исключив пиксели с низкой когерентностью, которые могут быть заполнены путем интерполяции (обычно методом ближайшего соседа, см. нижний ряд изображений на картинке ниже). Для нашего примера (см. ноутбуки по ссылкам выше) результат обработки исходной серии интерферограмм оказывается визуально "полосатым", на картинке ниже 0.1 градуса координатной сетки соответствуют примерно 10 км:
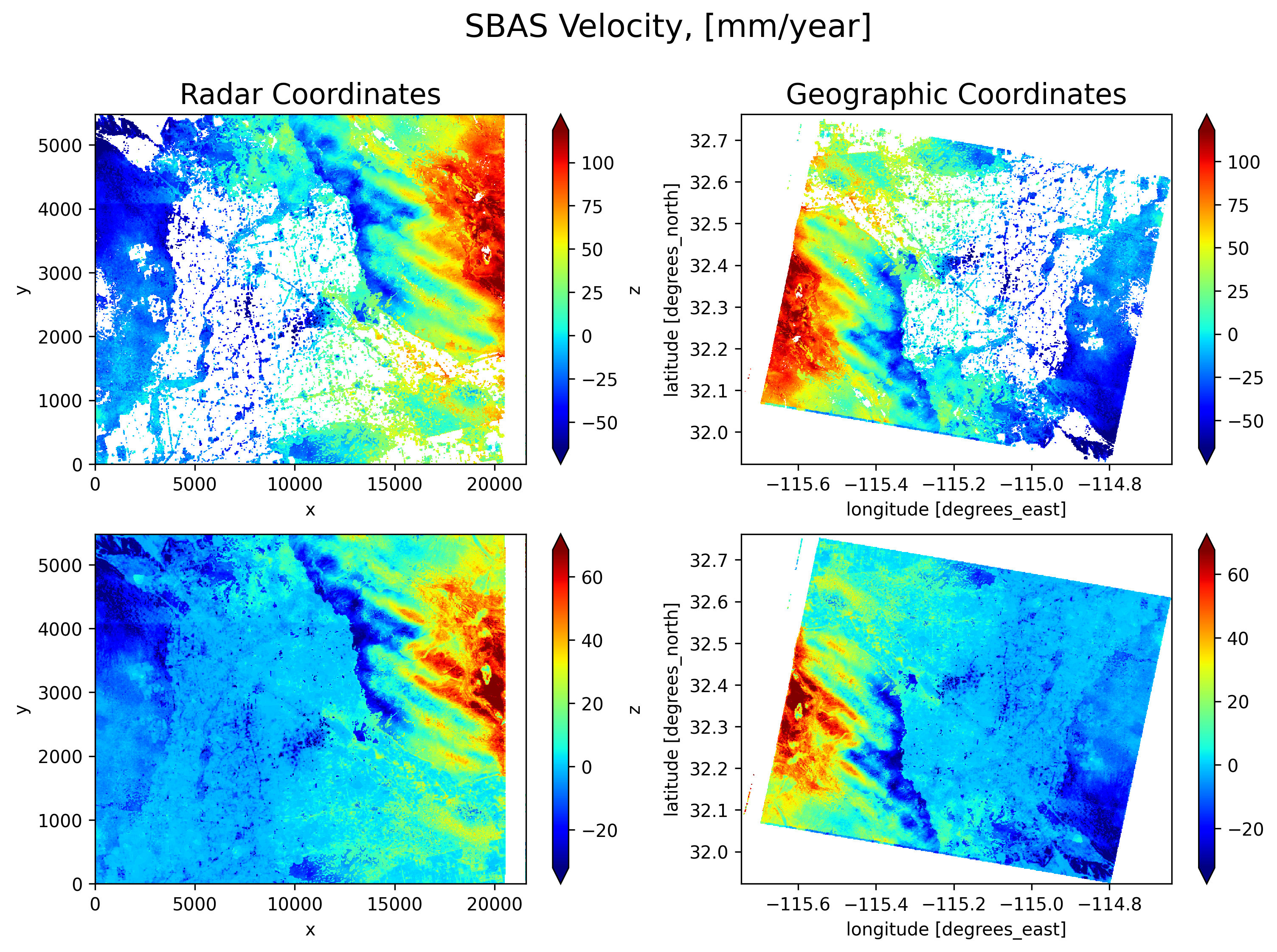
Как видим, атмосферная помеха всего лишь одного снимка сущесвенно исказила левую половину изображения в географических координатах. Тем не менее, правая половина карты годового смещения в географических координатах вполне может использоваться. Если же нас интересует вся выбранная территория целиком, необходимо найти способ исключить атмосферную помеху для всей территории.
Использование моделей атмосферы
Благодаря спутникам мониторинга атмосферы и различным моделям обработки данных наблюдений нам доступны оценки свойств атмосферы для любой территории в каждый момент времени. Достаточно лишь скачать соответствующий набор данных и вычислить атмосферную задержку. Этот подход более или менее успешно применяется для анализа с низким пространственным разрешением — все же точность атмосферных моделей не настолько высока, чтобы оценить влияние атмосферных эффектов километровых масштабов. Кроме того, результат зависит еще и от исследуемой территории и времени, поскольку точность моделей не постоянна. Не привожу здесь примеры такого анализа, поскольку оценка их точности практически невозможна, в то же время частично сохраняются визуально видимые помехи — так что сложно сказать, насколько этот способ улучшает результат.
Использование физических свойств атмосферы
Атмосферная помеха сильно отличается от случайно распределенной ошибки разницы фаз двух фазовых изображений, поскольку для рядом расположенных участков значение атмосферного набега фазы практически совпадает. Характерный масштаб атмосферных эффектов это километры и десятки километров, а разрешение интерферометрической съемки равно метрам или десяткам метров. Именно указанное соотношение масштабов делает невозможным определение атмосферных задержек с помощью параметра когерентности, обычно вычисляемом в пространственном окне 32х32 пиксела (масштаб сотен метров).
Очевидным решением является анализ достаточно больших областей, чтобы включать в себя более одной помехи, в том числе всей интерферограммы целиком. Для этого применим так называемый метод разделения спектра — можно с помощью полосового фильтра извлечь характерный для атмосферных помех диапазон частот и найти в нем пики, соответствующие зачастую регулярным атмосферным структурам. Если сравнить спектр выделенной атмосферной помехи с пространственным спектром рельефа, мы можем обнаружить их корреляцию — это объясняется тем, что потоки воздуха даже в высоких слоях атмосферы коррелируют с рельефом. Отсюда следует широко известный в узких кругах прием — опытные интерферометристы сразу же полагают помехой все области корреляции интерферограммы и рельефа (поскольку прямое влияние рельефа на интерферограмму должно быть исключено в процессе построения интерферограммы). Указанным путем возможно найти все интерферограммы с высоким уровнем атмосферных помех и определить проблемные снимки для их исключения из дальнейшего анализа или даже вычислить поправку для атмосферной задержки. Обычно вычисление поправки используется в случаях, когда просто исключить снимки нельзя (остается слишком мало снимков или нужны снимки за конкретные даты).
Посмотрим, как выглядит результат полосовой пространственной фильтрации интерферограммы с атмосферными помехами для пары снимков 2015-03-10 и 2015-04-27 (здесь мы используем приближенную оценку длины волны в географических координатах, для точного вычисления необходимо использовать соответствующую спроецированную систему координат):

Для получения более интуитивно понятного изображения следует аналогично обработать развернутую интерферограмму:
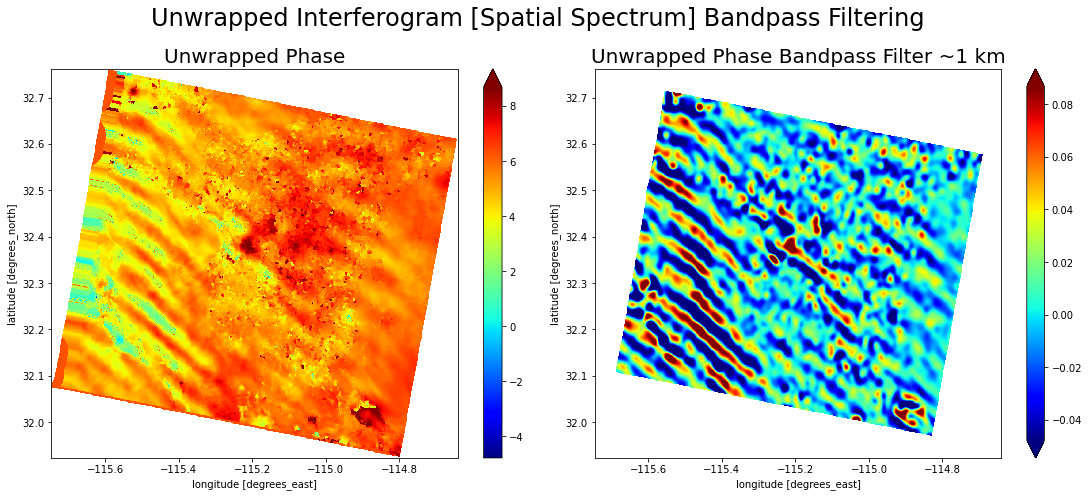
В обоих случая легко заметить, что атмосферные помехи отображаются явно различимой линейчатой структурой. Посмотрим для всех интерферограмм:
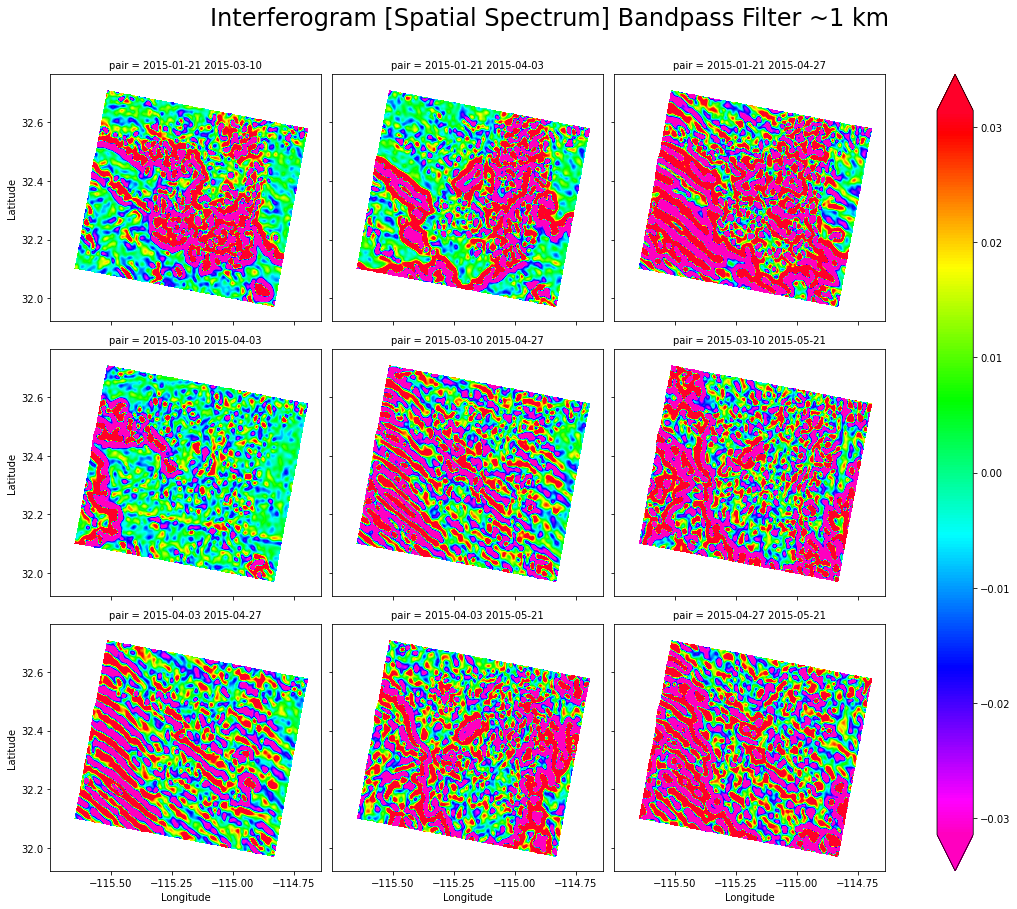
И аналогично для развернутых интерферограмм:
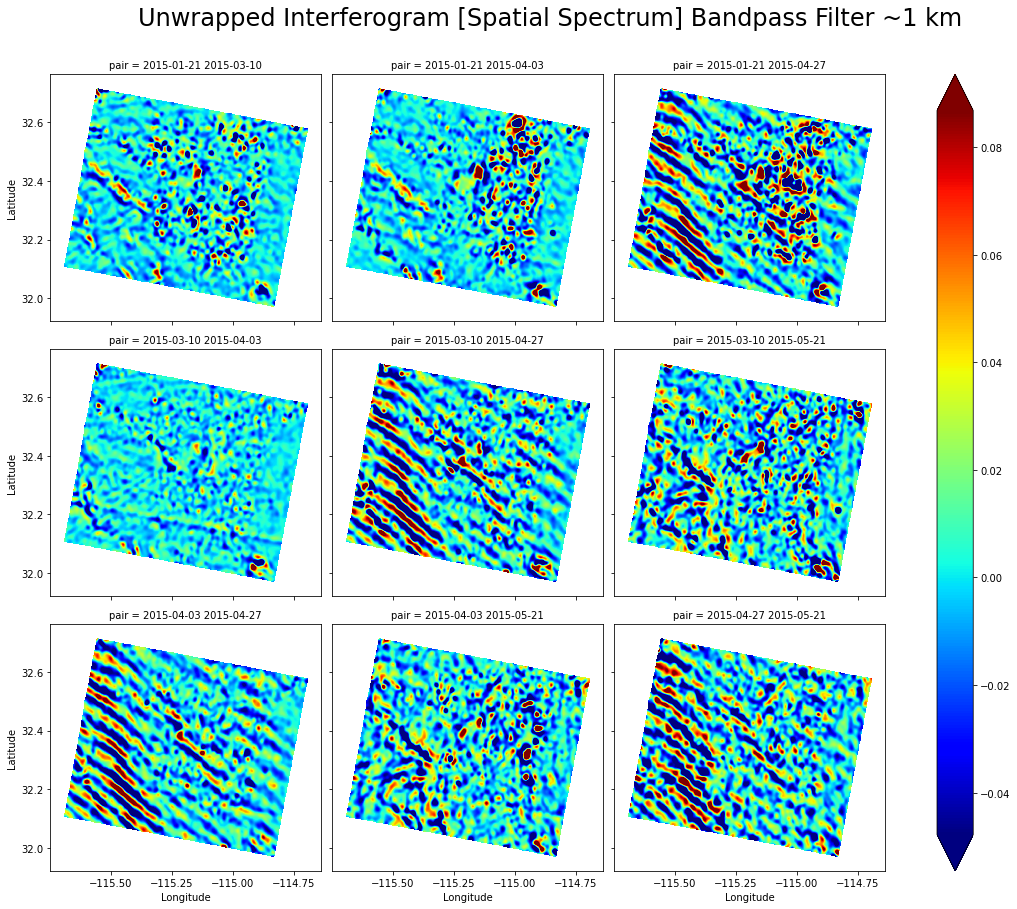
Выше на полученных 9 интерферограммах прекрасно видны 4 с атмосферными помехами на них. Заметим, что также выделяется субгоризонтальная полоса на интерферограмме '2015-04-03 2015-04-27', соответствующая некоторой ошибке совмещения полос исходных снимков (связано с самим процессом получения радарных снимков — полный снимок состоит из отдельных полос съемки, которые нужно правильно совместить). Далее удобно перейти к анализу спектров мощности интерферограмм в виде кривых фрактальной размерности (спектр мощности в двойной логарифмической шкале):

Легко объяснить наблюдаемый здесь эффект: атмосферная помеха привносит атмосферную задержку, которая в результате обработки превращается в ложное смещение земной поверхности, тем самым увеличивая значения спектра мощности для пространственных частот масштаба облаков. Для развернутой фазы этот эффект проявляется еще более явно:

В нашем случае характерный масштаб облачности оказывается равен 1-2 км. Важно учитывать, что интерферограмма является пространственным мультифракталом, это следует из того, что движения земной поверхности не изменяют общий объем планеты. И на масштабе порядка 1 км угол наклона кривой фрактального индекса резко уменьшается (и далее быстрее сходится к горизонтальной линии), в то время как атмосферная помеха продуцирует обратное поведение кривой.
Использование вычислительных методов
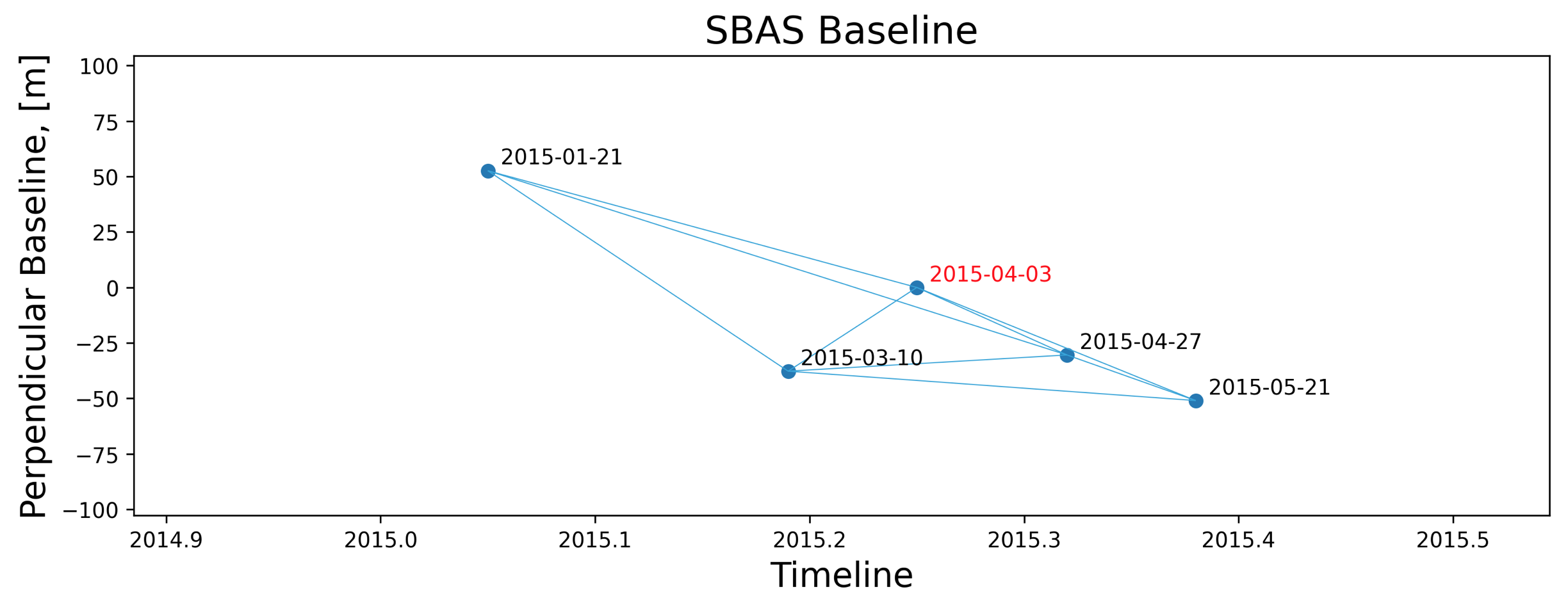
Есть и другой путь. В самом деле, при анализе достаточно большой территории мы ожидаем увидеть малые изменения средней высоты поверхности, иначе бы это означало значительные изменения радиуса и объема нашей планеты. В то же время, атмосферная задержка приводит к ошибкам разворачивания фазы (unwrapping) кратным числу pi. В реальности такая разница невозможна, поскольку, как уже указано, это означает изменение радиуса и объема планеты. Значит, для всех возможных замкнутых путей на SBAS диаграмме необходимо вычислить набег фазы и для значений, кратных pi, вычислить кратные pi поправки для всех интерферограмм так, чтобы обнулить набег фазы всех замкнутых путей SBAS диаграммы. Эти поправки позволят или (частично) компенсировать атмосферный набег фазы или просто исключить проблемные снимки. К такому подходу стоит прибегать тогда, когда почему-либо необходимо использовать все имеющиеся снимки, хотя непосредственное исключение зашумленных снимков обеспечит лучшие результаты.
Как быстрым и практически эффективным методом для исключения зашумленных снимков можно воспользоваться следующим подходом. Вспомним, что высокая корреляция интерферограммы с топографией, как правило, означает наличие коррелированных с топографией атмосферных помех. На SBAS диаграмме это равнозначно высокой положительной корреляции и с предыдущим и с последующим снимком для каждого треугольника (замкнутого пути, включающего три интерферограммы). Дело в том, что такая корреляция означает наличие (почти) только линейного тренда изменения для всего интервала наблюдения, что эквивалентно росту (или убыванию) радиуса и объема планеты, что физически невозможно и не может быть вызвано случайно распределенной ошибкой, таким образом, этот эффект создается именно атмосферной задержкой. На графике это выглядит так:
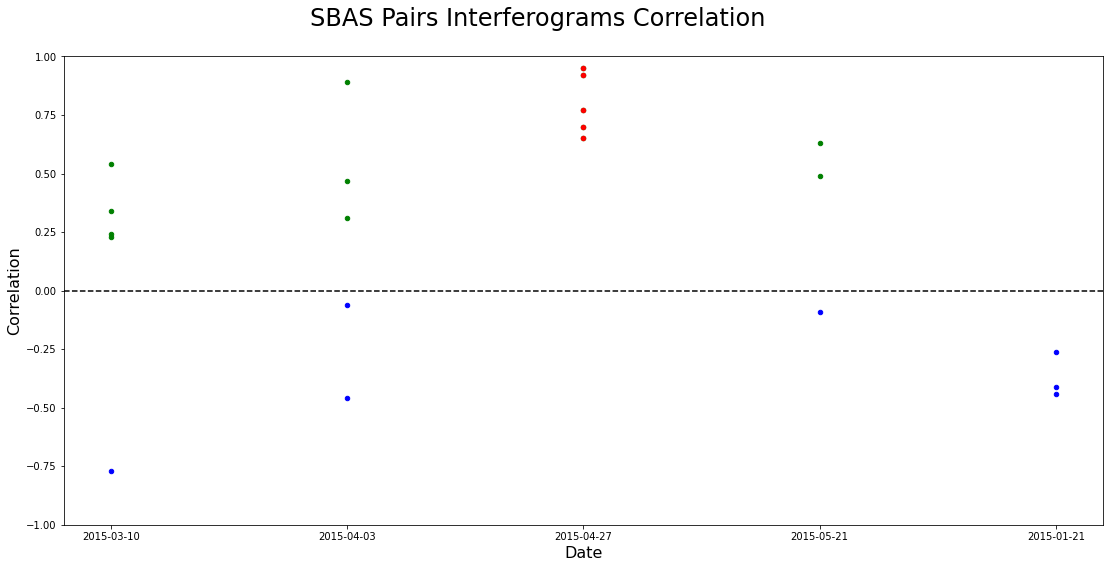
Здесь синими точками отмечены отрицательные значения корреляции, зелеными — положительные, а красные точки соответствуют случаю, когда для выбранного снимка присутствуют только положительные значения корреляции. Как и ожидалось, красные точки соответствуют именно зашумленному снимку. Конечно, для первого и последнего снимков допустимо наличие корреляции лишь одного знака — просто потому, что для них нет предшествующих и последующих снимков.
При использовании данного метода может возникнуть вопрос — всегда ли для произвольно выбранного снимка без атмосферных помех должны присутствовать корреляции разных знаков? Да, всегда, при том лишь условии, что периоды построенных интерферограмм охватывают разные фазы солнечных и лунных приливов — амплитуда и масштаб которых значительно превышает все остальные изменения уровня поверхности. Таким образом, эти приливы нам не только мешают, но и помогают, при правильном к ним подходе.
Я реализовал указанный подход в Live Google Colab Jupyter ноутбуке S1A_Stack_CPGF_T173 Plus и теперь результат обработки интерферометрической серии выглядит отлично:

Заключение
Мы рассмотрели различные подходы к решению проблемы атмосферной задержки при анализе данных спутниковой интерферометрии. Предпочтительные, на мой взгляд, методы проиллюстрированы рабочим кодом в Jupyter ноутбуках на GitHub и Google Colab. Показанные методы превосходят возможности, доступные во многих из современных интерферометрических пакетов, и позволяют выполнять не только вычисление постоянной составляющей (линейного тренда), но и периодических колебаний поверхности для поиска подземных резервуаров воды, нефти и газа, и даже анализа заполненности магматических камер и глубинных движений магмы. И рудные месторождения различного генезиса также приурочены к трещиноватым (фрактальным) участкам земной поверхности, связанным с глубинными разломами и геотермальными потоками. Именно для решения всех этих задач я взялся за написание своего открытого пакета спутниковой интерферометрии PyGMTSAR on GitHub, о котором постепенно и рассказываю в серии статей.
Также смотрите
- Мои статьи на Хабре
- Теоретические и практические статьи и посты на LinkedIn
- Геологические модели и код на GitHub
- YouTube канал с геологическими моделями
- [Геологические модели в виртуальной/дополненной реальности (VR/AR)](

