15.07.2022 09:47
m03r 7 6300 Источник

Однажды много лет назад один немолодой профессор задал мне задачку о перестановке стрелок часов. Точной формулировки за давностию лет я не помню, но поиск в интернете привёл меня к «Занимательной алгебре» Я. И. Перельмана, которая была впервые опубликована в 1933 году:


Возьмём положение стрелок в 12 часов. Если бы в этом положении большая и малая стрелки обменялись местами, они дали бы всё же правильные показания. Но в другие моменты, — например, в 6 часов, — взаимный обмен стрелок привёл бы к абсурду, к положению, какого на правильно идущих часах быть не может: минутная стрелка не может стоять на 6, когда часовая показывает 12. Возникает вопрос: когда и как часто стрелки часов занимают такие положения, что замена одной другою дает новое положение, тоже возможное на правильных часах?

Что любопытно, эта формулировка восходит к книге Александра Мошковского «Альберт Эйнштейн: беседы с Эйнштейном о теории относительности и общей системе мира», опубликованной в 1921 году на немецком языке, и уже в следующем году (!) переведённой на русский язык (и, судя по каталогу РГБ, с тех пор её и не переиздавали; доступен английский перевод).


Мошковский, навещая Эйнштейна во время болезни, предложил ему эту задачу для развлечения. Тот отметил, что задача интересная и не слишком простая, однако, увы, удовольствие от неё не продлится долго, потому что путь к решению уже ясен. Начертив условия задачи на листе бумаги, Эйнштейн составил диофантово уравнение и спустя небольшое время решил его.


К сожалению, более никаких подробностей в книге Мошковского не упоминается, и как могло бы выглядеть это уравнение, мы можем только предполагать. Решение, приведённое в книге Перельмана, в целом выглядит примерно так же, и довольно громоздко.


Решение, приведённое Перельманом

Пусть одно из требуемых положений стрелок наблюдалось тогда, когда часовая стрелка отошла от цифры 12 на $x$ делений, а минутная — на $y$ делений. Так как часовая стрелка проходит 60 делений за 12 часов, т. е. 5 делений в час, то $x$ делений она прошла за $\dfrac{x}{5}$ часов. Иначе говоря, после того как часы показывали 12, прошло $\dfrac{x}{5}$ часов. Минутная стрелка прошла $y$ делений за $y$ минут, т. е. за $\dfrac{y}{60}$ часов. Иначе говоря, цифру 12 минутная стрелка прошла $\dfrac{y}{60}$ часов тому назад, или через $\dfrac{x}{5}-\dfrac{y}{60}$ часов после того, как обе стрелки были на двенадцати. Это число является целым (от нуля до 11), так как оно показывает, сколько полных часов прошло после двенадцати. Когда стрелки обменяются местами, мы найдём аналогично, что с двенадцати часов до времени, показываемого стрелками, прошло $\dfrac{y}{5}-\dfrac{x}{60}$ полных часов. Это число также является целым (от нуля до 11).


Имеем систему уравнений:


$\begin{cases} \dfrac{x}{5}-\dfrac{y}{60}=m\\ \dfrac{y}{5}-\dfrac{x}{60}=n \end{cases}$


где $m$ и $n$ — целые числа, которые могут меняться от 0 до 11. Из этой системы находим:


$ x=\dfrac{60(12m+n)}{143}\\ y=\dfrac{60(12n+m)}{143} $


Давая им значения от 0 до 11, мы определим все требуемые положения стрелок. Так как каждое из 12 значений $m$ можно сопоставлять с каждым из 12 значений $n$, то, казалось бы, число всех решений равно 12 × 12 = 144. Но в действительности оно равно 143, потому что при $m = 0, n = 0$ и при $m = 11, n = 11$ получается одно и то же положение стрелок.


Я решал эту задачу примерно тем же образом и с некоторыми усилиями получил верный ответ, но спустя несколько лет мне пришла в голову следующая картинка: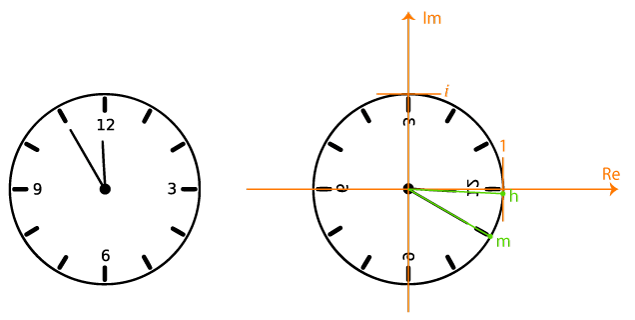
image


Мысленно положим часы циферблатом вниз на комплексную плоскость так, чтобы 12 часов были в точке $1$, а 3 часа — в точке $i$.


В этом случае положение стрелок часов легко выражается через комплексную экспоненту. Если время, прошедшее с полуночи в часах, обозначить как $t$, то положение конца минутной стрелки $m$ будет равно $e^{2\pi it}$, поскольку за каждый час минутная стрелка совершает ровно один оборот. Часовая же движется в 12 раз медленнее, и положение её конца (будь она длины 1) $h = e^{\tfrac{\pi}{6}it}$.


(Если предыдущий абзац совершенно непонятен, то рекомендую замечательные видео от 3blue1brown из серии Lockdown math)


Важно, однако, даже не это, а соотношение $h^{12}=m$.


Пользуясь этим соотношением, можно решать практически любые задачи о стрелках часов, причём делать это единообразно. Начнём с простого.


Сколько раз за 12 часов совпадают стрелки часов?


Стрелки совпадают, следовательно $h = m$. Отсюда:


$ \begin{cases} h = m\\ h^{12}=m \end{cases}\\ h^{12} = h $


Поскольку $h$ — точка на единичной окружности и никогда не равна нулю, то на $h$ можно смело делить (как и на $m$):


$ h^{11} = 1 $


Отсюда немедленно следует, что это случается 11 раз за двенадцатичасовой период через равные интервалы, начиная с $h = m = 1$, т. е. полуночи/полудня. Интервал составляет $\dfrac{12}{11}$ часа, то есть 1 час и $5\dfrac{5}{11}$ минут.


Сколько раз за 12 часов стрелки часов направлены в противоположные стороны?


Стрелки противонаправлены, следовательно $h = -m$. Отсюда аналогичным способом получаем:


$ h^{12} = -h\\ h^{11} = -1 $


Соответственно, подобные моменты случаются так же 11 раз за 12 часов с такими же равными интервалами, но только начиная не с $h=1$, а с $h=-1$, что соответствует 6 часам.


Сколько раз за 12 часов стрелки часов расположены под прямым углом друг к другу?


Эта задача немного сложнее, потому что прямой угол может быть как в одну сторону, так и в другую, то есть $h = i\cdot m$ или $h = -i\cdot m$.


Поскольку $\sqrt{-1} = \pm i$, то уравнение $h = \pm i\cdot m$ эквивалентно $h^2 = -m^2$. Далее аналогично подставляем $m=h^{12}$:


$ h^2 = -(h^{12})^2\\ h^2 = -h^{24}\\ h^{22} = -1 $


И получаем 22 положения за 12 часов с интервалом, соответственно, в $32\dfrac{8}{11}$ минут, начиная с 3 часов ($h = i$) или 9 часов ($h = -i$).


Сколько раз за 12 часов встречаются часовая, минутная и секундная стрелки?


Вспомним, что секундная стрелка движется в 60 раз быстрее минутной, следовательно её положение $s = m^{60} = h^{720}$. А если они все равны, то требуется решить уравнение $h = h^{12} = h^{720}$, которое в силу $h \neq 0$ можно преобразовать в $h^{11} = h^{719} = 1$ с единственным решением $h = 1$.


Аналогичным образом можно посчитать, что часовая стрелка с секундной встречаются 719 раз за 12 часов, а минутная с секундной — 708 раз за 12 часов (по 59 раз в час).


Когда стрелки стоят симметрично (т.е. на одинаковых расстояниях от 12)?


В общем случае здесь бы понадобилась операция комплексного сопряжения, но поскольку все наши точки лежат на единичной окружности, то достаточно минус первой степени: $m = h^{-1}$. Отсюда:


$ h^{12} = h^{-1}\\ h^{13} = 1 $


Тринадцать возможных положений, начиная с 12 часов и с интервалом в $\dfrac{12}{13}$ часа, то есть $55\dfrac{5}{13}$ минут.


В мире антиподов минутная стрелка идёт с нормальной скоростью, но в противоположную сторону. Сколько раз за сутки стрелки антиподных часов а) совпадают; б) противоположны; в) расположены под прямым углом?


Поскольку в мире антиподов минутная стрелка идёт в противоположную сторону, то здесь $m_{anti}=m^{-1}=h^{-12}$.


Думаю, читатель к этому моменту уже наловчился решать подобные уравнения в уме, и может легко сообразить, что у уравнений $h = h^{-12}$ (для совпадающих стрелок) и $h = -h^{-12}$ (для противоположных стрелок) будет по 13 ненулевых решений.
Прямому углу между стрелками соответствует уравнение $h = \pm i \cdot h^{-12}$, то есть $h^2 = -h^{-24}$: целых 26 решений с интервалом $27\dfrac{9}{13}$ минут.


Ну что же, пора перейти к задачке, с которой всё начиналось.


Когда и как часто стрелки часов занимают такие положения, что замена одной другою даёт новое положение, тоже возможное на правильных часах?


Для любого корректного положения стрелок, как мы помним, верно равенство $m = h^{12}$. Соответственно, чтобы обмен стрелок также давал корректное положение, требуется, чтобы было верно и $h = m^{12}$. Отсюда:


$ \begin{cases} h = m^{12}\\ m = h^{12} \end{cases}\\ h = h^{144}\\ h^{143} = 1 $


Итого — 143 возможных положения с равными интервалами в $5\dfrac{5}{143}$ минут в течение 12 часов. Весьма лаконично, если сравнивать с другими способами решения, не правда ли?

Комментарии (7)


  1. VladK69
    15.07.2022 19:39
    #24531484
    +2

    Мегасложные решения приводятся, прочитать не осилил).

    Давайте в декартовых координатах 2пи х 2пи (угол часовой, угол минутной) отметим допустимые положения стрелок. Это 12 линий с пологим наклоном. Если мы меняем стрелки, отображаем эти линии через биссектрису. Получаем 12 почти вертикальных линий. Итого 144 пересечения, но "12часов" задваивается, исключаем. Решение: 12*12-1=143


    1. m03r Автор
      15.07.2022 19:50
      #24531514

      Какое любопытное графическое решение! Но и тут требуется дополнительный шаг, чтобы убрать «задвоение» 12 часов


  1. karambaso
    15.07.2022 19:54
    #24531526
    +6

    Декартовы коодинаты и комплексная экспонента не нужны.

    Есть такая штука - сравнения по модулю. К ним применимы многие алгебраические преобразования, привычные нам со школы. Отсюда вытекает возможность пропустить все эти экспоненты и сразу записать: 12ht=ht (mod 360). Это для одинакового положения стрелок. Перенося получаем: 11ht=0 (mod 360). Или 11ht=360*k (mod 360). Откуда ht=k*360/11, или примерно каждые 32 градуса, или каждые пять минут с секундами.

    Аналогично отвечаем и на все остальные вопросы.


    1. m03r Автор
      15.07.2022 23:10
      #24531880

      Да, по сути это то же самое. При этом для меня, честно говоря, комплексную экспоненту гораздо проще визуализировать в контексте часовых задач.


  1. JPEGEC
    16.07.2022 06:52
    #24532190

    Смутное чувство что это все справедливо для равномерного движения стрелок.

    Вот только в реальности это не так. А сильно зависит от конструкции конкретных часов.


    1. chersanya
      16.07.2022 12:08
      #24532530

      Точно, для дискретно двигающихся секундной-минутной стрелки было бы интересно увидеть обобщение :)


      1. m03r Автор
        16.07.2022 12:23
        #24532560

        Если изменение состояния часов происходит раз в минуту (т. е. минутная ходит по 1/60 круга, а часовая — по 1/720), то получаем дополнительное ограничение h^{720}=1, которое оставляет одно или два решения.

        Или предполагается, что одна стрелка движется рывками, а другая непрерывно?