Объяснение популярной минимаксной игры GAN и функции общих потерь модели

Генеративно-состязательные сети (GAN) приобрели известность не так давно. Наиболее популярны эти сети в области машинного зрения. К старту нашего флагманского курса по Data Science рассказываем, какая математика у них под капотом.

С выходом статьи «Генеративно-состязательные сети» (Generative Adversarial Nets) Йена Д. Гудфеллоу и соавторов^[1] появились новая стратегия разработки генеративных моделей и, как следствие, множество работ и проектов, посвящённых разработке приложений, которые вошли в последние версии DALL-E 2^[2] и GLIDE^[3].

В обоих приложениях используются новое воплощение генеративных моделей — диффузионные модели, но по сей день GAN остаются популярными. Они подходят для решения множества прикладных задач.

Вначале хочется поговорить о знакомой всем первоначальной функции оптимизации для GAN, рассказать о её отличиях от общей функции потерь в модели. Должно быть, вы знаете, что позднее появились варианты функции потерь.

1. Краткое введение в генеративно-состязательные сети

Генеративно-состязательные сети — это класс фреймворков глубокого обучения со структурой генеративной модели. Их задача — генерировать новые, сложные (выходные) данные: например, изображения или аудиофайлы, которых до генерации не существовало.

Для обучения GAN нужен только набор данных (изображений, аудио и т. п.), которые хочется скопировать или имитировать. Сеть сама определит способы создания новых данных, которые будут выглядеть как данные из полученного сетью набора данных.

Иными словами, примеры показываются, чтобы вдохновить модель. Ей даётся полная свобода творчества.

Обучение, при котором на вход нейросети подаётся нечто без каких-либо описаний и данных о нужных итогах генерации, называется неконтролируемым обучением.

Архитектура GAN включает две состязающиеся между собой нейросети. Отсюда и слово «состязательные» в названии. Эти две сети называются генеративной (G) и дискриминационной (D) или просто генератором и дискриминатором соответственно. Задача генератора — изучить функцию генерации данных, начиная со случайного шума. Дискриминатор должен определить, является ли образец данных «подлинным». При этом «подлинностью» считается принадлежность к образцам исходного набора данных. Это позволяет измерить эффективность модели и отрегулировать её параметры. Обе нейросети обучаются одновременно.

Вы можете представить себе антагонистическую игру генеративной (G) и дискриминативной (D) сетей так: мошенник по кличке Генератор (справа создаёт подделки, пытаясь одурачить детектива Дискриминатора (слева)

Обучение GAN

Есть великое множество вариантов и модификаций обучения GAN. Однако, следуя плану первой работы в этой области [1], прежде всего рассмотрим базовый цикл обучения GAN. Этот цикл повторяется:

1. Сгенерировать m образцов (изображения, аудио, и т. п.) из распределения выборки (случайный шум z), который мы обозначим как: G(z).
2. Взять m образцов из набора для обучения: x.
3. Смешать все примеры (из начального набора и сгенерированные) и передать их дискриминатору D Выходные данные D варьируются между «0» и «1»: «0» означает, что образец — «фальшивка», а «1» — «подлинность» образца.
4. Измерить функцию потерь дискриминатора и отрегулировать параметры.
5. Сгенерировать m новых образцов G’(z).
6. Передать G’(z) дискриминатору. Измерить функцию потерь дискриминатора и отрегулировать параметры.

Более современные подходы к обучению GAN включают измерение потерь генератора и регулировку его параметров, пока дискриминатор проходит этап 4, при этом этапы 5 и 6 пропускаются, чтобы сэкономить время и ресурсы компьютера.

2. Функции оптимизации и потерь (минимаксная игра)

Если вы читали первую статью о GAN, то знакомы с так называемой функцией оптимизации этой модели.

Функция оптимизации GAN. Скриншот из работы «Генеративно-состязательные сети» (Generative Adversarial Nets) [1]

Представленная формула описывает функцию оптимизации. Это выражение пытаются оптимизировать обе нейросети (генератор и дискриминатор). Но если G стремится её уменьшить, то D пытается её увеличить. Тем не менее эта функция не является общей функцией потерь, определяющей эффективность всей модели.

Чтобы понять суть минимаксной антагонистической игры, нужно разобраться с измерением производительности модели, чтобы нейросети могли их оптимизировать. Поскольку архитектура GAN представлена двумя одновременно обучаемыми нейросетями, нужно вычислить два параметра: потери генератора и потери дискриминатора.

Функция потерь дискриминатора

Согласно циклу обучения (в работе [1]) дискриминатор получает одну серию образцов m из набора данных, а другую серию образцов m — от генератора. На выходе у него число ∈ [0,1], выражающее вероятность принадлежности входных образцов набору данных для обучения (то есть «подлинность» данных).

Уже до поступления образцов в дискриминатор нам известно, какие из них подлинные, а какие были сгенерированы (образцы x из набора данных для обучения являются подлинными, а G(z) выданы генератором). Поэтому мы можем обозначить их: y = 0 (сгенерированные), y = 1 (подлинные).

Рисунок 1. Принцип работы модели GAN. k — любые входные данные дискриминатора, которые могут быть сгенерированными или подлинными образцами из набора

Теперь мы можем обучить дискриминатор классической бинарной классификации при помощи функции потерь бинарной перекрёстной энтропии:

Формула бинарной перекрёстной энтропии дискриминатора (D), где n = 2m. y_i соответствует обозначениям, а k — любым входным данным (генерируемым и подлинным)

Поскольку это бинарный классификатор, сложение приводит к чередованию:

• Если образец подлинный, обозначение y = 1 → сумма ∑ = log(D(k)).
• Если образец сгенерирован, обозначение y = 0 → сумма ∑ = log(1-D(k)).

Выражение можно упростить:

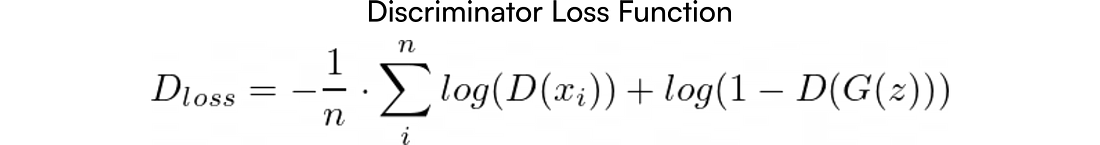
Теперь x_i — это подлинный образец из набора данных для обучения, а G(z) создан генератором (G). Мы одновременно передаём функции не один, а два набора входных данных: D(X_i) и G(z). При этом n = m.

Функция оптимизации

Как мы уже знаем, дискриминатор пытается свести к минимуму свои потери, а значит, и значение приведённого выше выражения (argmin Dloss). Однако выражение можно изменить, то есть убрать из него минус. Теперь вместо минимизации значения выражения его нужно будет максимизировать:

Ранее мы минимизировали выражение, чтобы получить Dloss = 0. Теперь мы поменяли знак, и для получения -Dloss = 0 нам нужно максимизировать его

Наконец, выражение можно привести к такому виду:

Окончательное выражение для -Dloss. Ex~p(x) показывает ожидаемую величину.

Теперь перепишем выражение так:

Функция оптимизации дискриминатора (Discriminator Loss Function)

С другой стороны, генератор стремится обмануть дискриминатор. Поэтому он сделает обратное тому, что делает дискриминатор, и найдёт минимальное значение V(G,D).

.

Функция оптимизации генератора (Generator Loss Function)

Теперь оба выражения (функции оптимизации генератора и дискриминатора) можно сложить. Получится такое выражение:

.

Минимаксная антагонистическая игра

Функция оптимизации, наконец-то, у нас. Но, как я уже говорил, это не общая функция потерь, выражающая общую эффективность модели. Прежде чем мы перейдём к этой функции, нужно вычислить потери генератора:

Функция потерь генератора

Посмотрим ещё раз на функцию оптимизации. Во втором члене выражения фигурирует только генератор E(log(1-D(G(z))), а первый член имеет постоянную величину. Поэтому функция потерь генератора, которую он пытается уменьшить, описывается так:

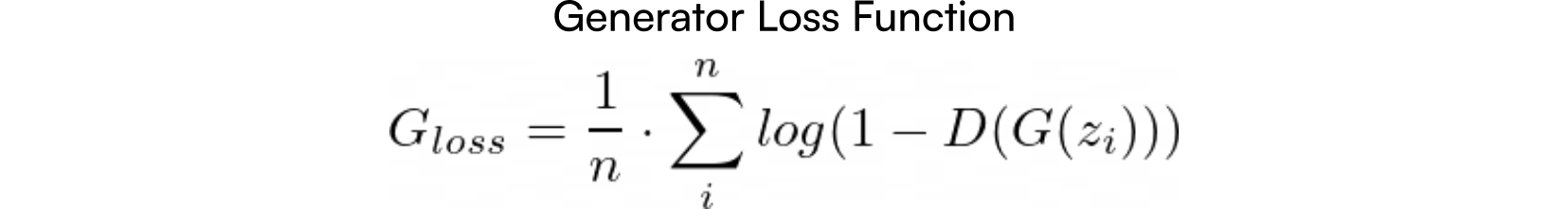
Но мы ещё не закончили. Как объясняется в первой работе, «в начале обучения, когда G не хватает навыков, D может с высокой долей уверенности браковать образцы, поскольку они сильно отличаются от данных исходного набора». Иными словами, на ранних стадиях обучения дискриминатору легко отличить подлинные образцы от подделок, поскольку генератор ещё не обучен. В этом случае функция log(1 − D(G(z))) насыщена, так как D(G(z)) ∼ 0.

Чтобы этого избежать, исследователи предлагают следующее: «Вместо того чтобы обучать G минимизации log(1 − D(G(z))), мы можем научить G максимизации log D(G(z))»

Иными словами, вместо обучения генератора минимизации вероятности подделки можно максимизировать вероятность подлинности образца.

Оба подхода к оптимизации едины по своей сути, что видно на этом графике:

Минимизация log(1-x) в диапазоне [0,1] идентичная максимизации log(x). График построен автором

Итак, мы будем пользоваться функцией потерь генератора, приведённой к виду:

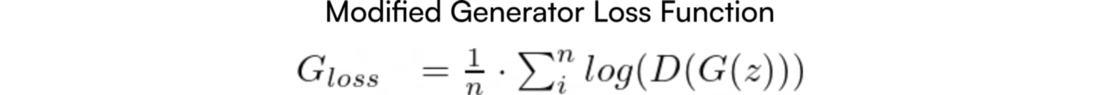
Ненасыщаемая функция потерь генератора. Помните, что теперь G хочет максимизировать эту функцию.

На практике функция потерь генератора, как правило, приводится к отрицательному выражению. Поэтому вместо максимизации её нужно минимизировать. Это упрощает настройку параметров при помощи такой библиотеки, как Tensorflow. Важно также понимать, какова общая функция потерь. Ей посвящён следующий раздел.

3. Общая функция потерь

В этой статье описаны формулы потерь каждого компонента (генератора и дискриминатора) и функция оптимизации модели. Но это не даёт ответа, как измерить общую эффективность модели.

Визуальной оценки функции оптимизации недостаточно. Как мы уже видели, функция оптимизации является видоизменённой функцией потерь дискриминатора. Поэтому она не отражает эффективности генератора (в этой формуле мы учитываем только эффективность работы дискриминатора, хотя функция потерь генератора и выводится из неё).

С другой стороны, есть возможность сложить обе функции потерь (дискриминатора и генератора), и, как подсказывает интуиция, нам нужно учесть ряд нюансов:

1. Каждая частная функция потерь должна стремиться к максимуму или минимуму.

В противном случае ошибка при сложении будет больше или меньше, чем нужно.
Например, возьмём функцию оптимизации, которую стремится максимизировать D:

и функцию потерь генератора, которую стремится минимизировать G:

.

При плохой работе D (маленькая ошибка) и хорошей работе G (маленькая ошибка) общая эффективность будет иметь маленькую ошибку. Таким образом, обе нейросети (G и D) в совокупности работают отлично, хотя мы и знаем, что для одной из них это не так.
Кроме того, если одна из функций потерь стремится к минимуму, а другая — к максимуму, мы не сможем понять, хорошо это или плохо — иметь высокую ошибку.

Если используемые функции потерь стремятся к максимуму, использовать термин «ошибка» (Error) нелогично, поскольку, чем выше такая «ошибка», тем выше эффективность. Однако всё меняется при использовании логарифмической шкалы: log(1+"Error").

2. Чтобы построить общую функцию потерь, отдельные потери должны иметь общий порядок величины.

Приведём пример функции потерь дискриминатора, которую мы обсуждали в начале статьи (бинарную перекрёстную энтропию):

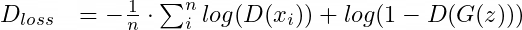
и функцию потерь генератора, к которой мы в итоге пришли:

.

Теперь обе функции стремятся к минимуму, как того требуют условия. Однако функция потерь дискриминатора лежит в диапазоне [0, +∞), а функция потерь генератора выдаёт значения (-∞,0]. Сложить эти две функции — значит, вычесть потери генератора. Поэтому мы можем сказать, что общая функция потерь равна потерям дискриминатора за вычетом влияния генератора (то есть E(log(D(xi))), где E — ожидаемое значение), и это неправильно.

Однако можно использовать другую комбинацию слагаемых. Что, если мы сложим первую функцию потерь дискриминатора и отрицательную форму функции потерь генератора?

Общая функция потерь модели GAN. Она отражает общую эффективность модели

(Ура!) Общая функция потерь GAN, наконец, найдена. Однако, если вы мне не верите, давайте проверим, удовлетворяет ли она параметрам.

✅ 1. Мы знаем, что Dloss стремится к минимуму и функция потерь генератора в отрицательном виде (Modified Generator Loss) тоже стремится к минимуму.

✅ 2. Dloss может выдавать значения в диапазоне [0, +∞). Таким образом, отрицательная функция потерь генератора выдаёт значения в том же диапазоне.

То есть мы добавляем ошибки в той же категории. Таким образом мы рассчитываем общую функцию потерь модели.

4. Заключение

Подытожим ключевые моменты этой статьи:

1. Функция оптимизации GAN (также называемая минимаксной игрой) и общая функция потерь отличаются друг от друга:
   Минимаксная оптимизация ≠ Общая функция потерь.
2. Функция оптимизации выводится из функции бинарной перекрёстной энтропии (а та, в свою очередь, — из функции потерь дискриминатора). Отсюда же выводится функция потерь генератора.
3. На практике функция потерь генератора приводится к виду, в котором логарифмическое выражение является ненасыщенным. Общая функция потерь модели также рассчитывается после такого приведения.
4. Общая функция потерь = Dloss + Gloss. Не все формулы можно использовать, и нужно учесть два ключевых момента:
   
   • Обе частных функции потерь нужно минимизировать или максимизировать.
   • Частные функции потерь должны иметь общий порядок величины

Надеюсь, моя статья будет интересной и полезной для вас. Не стесняйтесь оставлять комментарии. Любые замечания и предложения по ней приветствуются.

Научим разрабатывать сети GAN и работать с данными, чтобы вы прокачали карьеру или стали востребованным IT-специалистом:

• Профессия Data Analyst (12 месяцев)
• Профессия Data Scientist (24 месяца)

Чтобы посмотреть все курсы, кликните по баннеру: