Меня зовут Азат Якупов, я люблю данные и люблю использовать их в разных задачах. Сегодня хочу поделиться своим опытом относительно B-Tree индексов в PostgreSQL. Рассмотрим их топологию, синтаксис, функциональные B-Tree индексы, условные B-Tree индексы и включённые B-Tree индексы.

Этот материал — немного сокращённый пересказ моего выступления. Если вам комфортнее смотреть видео, чем читать текст, можно сделать это на YouTube. Таймкоды есть в описании.
Содержание
Что такое индекс
Представьте, что вам нужно найти определённую фразу в книге. Вы не знаете, где конкретно она расположена, а значит, вам предстоит листать все страницы и искать фразу глазами. Время такого поиска линейно: если вы тратите 1 секунду на 1 страницу, а всего страниц 1 000 000, то на поиск фразы понадобится 1 000 000 секунд. Придётся пролистать книгу до конца, ведь фраза может не быть уникальной и встречаться несколько раз.
На графике такой поиск показывает красная прямая:

Сократить время поиска поможет индекс. Он даёт возможность использовать логарифмический или бинарный поиск, который позволяет «гнуть» нашу прямую логарифмом. Вместо 1 000 000 изначальных секунд мы потратим на тот же поиск логарифм от миллиона, то есть 13 с копейками секунд. На графике выше это иллюстрирует зелёная кривая.
Давайте посмотрим на пример в работе с данными. Допустим, у меня есть запрос и поле, по которому я ищу без индекса:
SELECT ID, NAME
FROM Employee
WHERE NAME = 'Kate'Чтобы найти Екатерину, нужно смотреть каждую страницу, где расположены записи, и идти от записи к записи. То есть нужно перебрать все данные. Это выглядит как подход полного перебора данных (brute force). Отсюда происходит понятие последовательного чтения или sequential scanning — последовательное сканирование данных. Очевидный минус такого поиска — он не очень быстрый. Чем больше строк в базе данных, тем больше будет время поиска элементов. Схематично последовательное чтение выглядит так:

В случае, когда тот же атрибут NAME проиндексирован, мы ищем его не по всей таблице, а внутри B-Tree структуры. Ниже я схематично показал эту структуру пирамидой. Смысл в том, что при поиске мы сначала попадаем в индексную структуру, и затем от корня делаем простые шаги перехода с уровня на уровень. Цель — попасть в лист дерева, который находится в конце пирамиды, и найти в нём адрес записи, соответствующей Екатерине:

Итак, мы ищем Екатерину по атрибуту NAME. Если атрибут проиндексирован, то какой-то лист содержит значение «Екатерина». Когда мы попадаем в лист дерева, индексная структура даёт нам информацию адреса расположения: block=7, offset=2. Мы адресно идём на эту страницу и вычитываем нужные данные, не перебирая все данные таблицы.
Проведу аналогию с почтовым адресом. Когда вы отправляете письмо, то указываете на конверте индекс, улицу, дом и квартиру. Так почтальон сможет отнести письмо правильному получателю. С B-Tree индексом в PostgreSQL история точно такая же: он нужен сначала для того, чтобы вы поняли, куда нести письмо. Так что B-Tree индекс — это точная структура, ускоряющая поиск. Её задача — всегда находить конкретные адреса, по которым вы сможете пойти в основной файл данных таблицы и вычитать нужное значение.
Таблица в PostgreSQL представлена в виде файла данных, лежащего на диске. Для того, чтобы обеспечить логарифмический поиск, имеется дополнительный файл, соответствующий индексу, который помогает искать информацию внутри таблицы.
Файл с индексом должен всегда находиться в синхронном состоянии с таблицей. Важно знать, что когда мы создаём индекс на таблице, а потом делаем операции изменения данных, например, INSERT, UPDATE или DELETE, то получаем некое замедление. Оно возникает ровно потому, что в синхронном режиме происходит обновление не только самой таблицы, но и индексного файла.
Как представляется индекс в PostgreSQL
Итак, индексная структура — это отдельный файл данных, который лежит вместе или рядом с файлом данных таблицы. Рядом потому, что мы можем создать отдельное табличное пространство для хранения индекса. Когда мы создаём индекс, база данных фиксирует его в своих метаданных вплоть до того, где и по какому пути находится тот или иной файл, соответствующий индексу.
Команда для создания обычного B-Tree индекса следующая:
CREATE INDEX idx_user ON test.user (id);Здесь мы создаём индекс с именем idx_user на таблице user в схеме test для поля id, который будем использовать в дальнейших примерах.
Давайте посмотрим, что мы можем узнать о нашем индексе из метаданных базы данных. Ответ на запрос показан на иллюстрации слева:
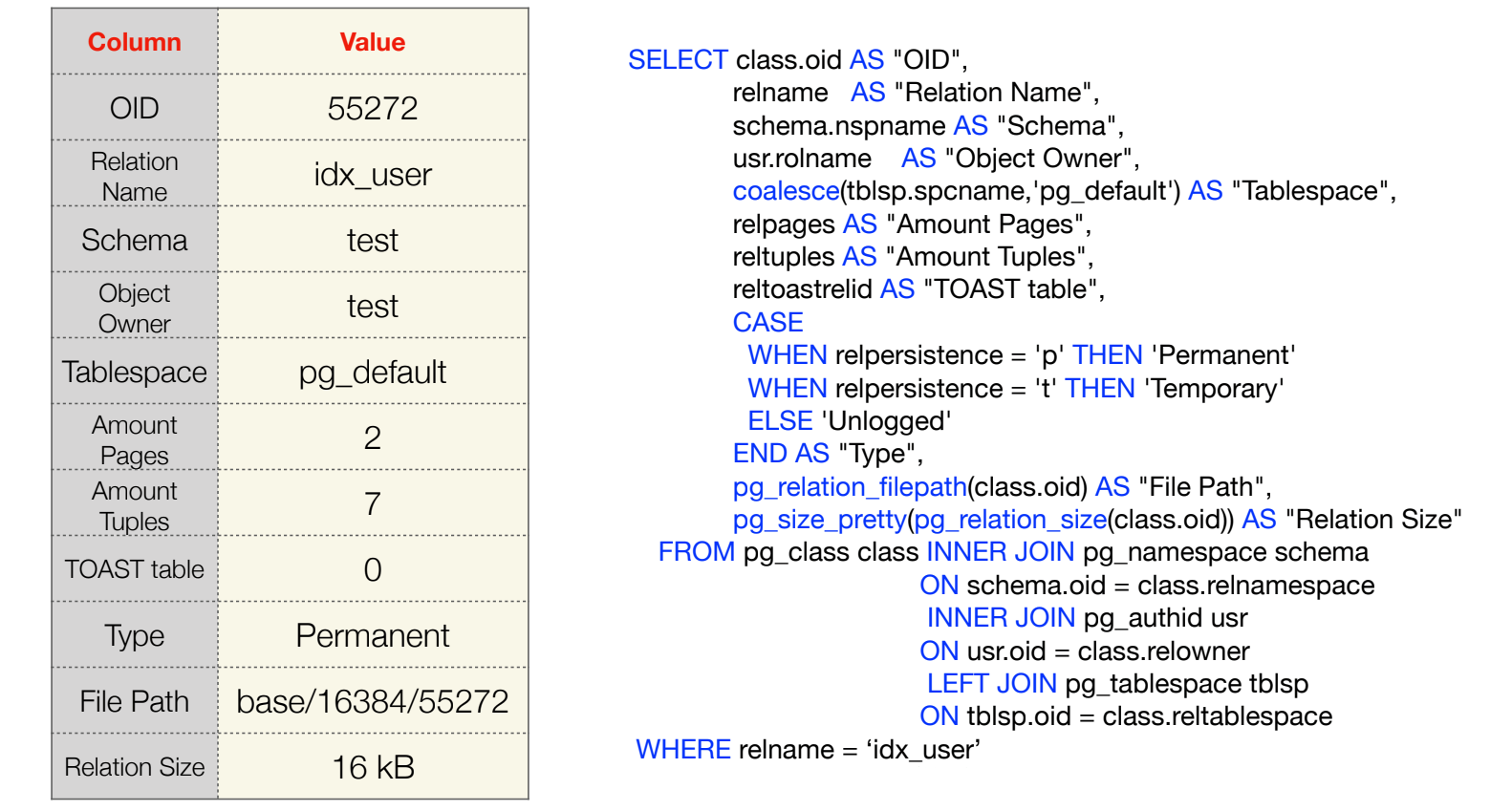
В метаданных мы видим:
OID или идентификатор объекта — внутренний идентификатор, который характеризует объект индекса внутри метаданных PostgreSQL.
Relation name — имя объекта.
Schema — схему, где определён объект индекса.
Object owner — хозяина этого объекта, под каким пользователем он был создан.
Tablespace или табличное пространство, где определён наш индекс. Я не делал дополнительных табличных пространств, поэтому он «упал» в то табличное пространство, которое установлено для базы данных по умолчанию.
Amount pages — количество страниц.
Amount tuples — количество записей.
TOAST tables или TOAST-таблицы.
Type — тип индекса, у нас он постоянный.
File path — путь, где лежит файл, который определяет структуру индекса.
Relation size — общий размер, который мы можем прочитать через функцию pg_relation_size. Он равен 16 килобайтам, потому что у нас две страницы. Каждая из страниц по правилам PostgreSQL весит 8 килобайт.
Теперь посмотрим на уровень диска. Выполнив команду ls -l, мы увидим файл с именем 55272, который соответствует внутреннему идентификатору нашего индекса, размером 16384 байт. Имя файла 55272 соответствует пути, указанному в метаданных:

А теперь посмотрим на логическое представление B-Tree индекса. У нас есть таблица, которая содержит произвольные строки. Они могут находиться в хаосе, не обязательно в упорядоченном виде. Дерево, которое строится на основании индекса, можно показать примерно так:

У нас имеется поддерево слева и поддерево справа от корня дерева. Левое поддерево содержит значения, которые всегда строго меньше корня, а правое поддерево — значения большие или равные корню.
Это свойство работает не только для корня, но и для любого внутреннего узла. Например, если мы попадаем на внутренний узел, где хранится значение 7, то значения слева будут строго меньше нашего узла, а справа — больше или равны ему. Благодаря этому вы точно знаете, куда идти, в зависимости от поиска.
Листья дерева повторяют значения строк оригинальной таблицы. Они представлены в порядке возрастания или убывания. Порядок зависит от того, как вы создавали индекс: использовали команду DESC или ASC. По умолчанию индексное дерево будет строиться в возрастающем порядке.
Представим, что мы ищем число 37. Мы заходим в корень и сравниваем: 13 > 37? Нет, поэтому дальше мы идём направо. После этого попадаем в следующий узел, где должны также принять новое решение, куда нам идти. В данном примере 37 лежит в диапазоне между 31 и 41. Мы переходим в соответствующий узел на третьем уровне, и уже там можем получить адрес строки, которая соответствует поисковому элементу 37. Мы пойдём на адрес конкретной страницы, в конкретную запись этой страницы, и получим информацию, не перебирая всю таблицу от и до.
Дальше давайте посмотрим, что лежит внутри индекса. Чтобы посмотреть, как устроена страница для индекса, я использую библиотеку pageinspect. Предварительно очищаю таблицу user, чтобы никаких не было грязных следов от данных и после этого добавляю новую строку. Затем использую API pageinspect, вызываю функцию bt_metap, которой передаю имя моего индекса idx_user:
CREATE EXTENSION IF NOT EXISTS pageinspect;
TRUNCATE TABLE test.user;
INSERT INTO test.user VALUES (1, 'Row #1');
SELECT *
FROM bt_metap('test.idx_user');Мне вернутся метаданные — разная техническая информация, а также информация по странице, которая является корнем. Это fastroot, объясняющий, как можно поступать в дальнейшем поиске, развивая топологию дерева.

В нашем случае fastroot равен 1, предполагается, что 1 — это номер страницы индекса. Давайте заглянем в эту страницу с помощью функции bt_page_stats, которая возвращает статистику по странице для B-Tree индекса:
SELECT *
FROM bt_page_stats('test.idx_user', 1);
Самые интересные элементы я выделил серым фоном. Btpo_prev и btpo_next показывают, есть ли у нашей страницы страница слева или справа. Type L, то есть leaf — лист, определяется таковым потому, что в нашей таблице ровно одна запись. Это значит, что наш корень также играет роль листа. В колонке live_items мы видим живые элементы, значение равно 1, потому что мы сделали один INSERT.
Чтобы посмотреть, какие конкретно элементы содержатся в этой единственной странице, используем функцию bt_page_items:
SELECT *
FROM bt_page_items('test.idx_user', 1);Функция возвращает нашу единственную живую запись:

У записи есть собственный ctid — это адрес, куда нам надо идти и смотреть. И есть данные, которые соответствуют типу bigint, 8 байт. Напоминаю, что мы индексировали только поле ID, поэтому в данных строка 1 не присутствует как значение.
Как всё это выглядит с точки зрения топологии? В реальности индекс мало похож на то, что рисуют в книгах:

Страница #0 — это всегда метастраница для индекса. Затем метастраница #0 ссылается на страницу #1 с нашими данными. Так как мы вставили одну строку, то корень дерева у нас совпадает с листом, и элементы нашего индексированного столбца находятся прямо в корне. Адрес ctid (0, 1) – это как раз адрес нашей строки в файле таблицы.
Пойдём чуть глубже и усложним наш тест. В этот раз я вставлю не 1 строку, а 1000:
TRUNCATE TABLE test.user;
INSERT INTO test."user"
SELECT i, 'Row #'||i::VARCHAR
FROM generate_series(1,1000) AS k(i)
SELECT *
FROM bt_metap('test.idx_user');Теперь fastroot = 3:

Заглянув в третью страницу, мы получаем статистику по странице #3 нашего индекса. Здесь появился тип R — root или корень. У него есть три живых элемента, мёртвых записей нет, потому что сделали чистый INSERT без UPDATE или DELETE:

В элементах страницы мы тоже увидим три живых строки.

Хочу обратить внимание, что адреса ctid здесь — это не адреса в data-файлах, а адреса на страницах внутри самого индекса. Мы находимся в корне, а корень содержит адресное состояние тех узлов, которые находятся под ним.
Если посмотреть в данные (data), то второй элемент — 367, если перевести всё в систему нормального исчисления, а последним элементом на нашей странице будет 733.
Нарисуем схему логической топологии нашего нового индекса. Метастраница — это страница #0, корень — #3, и в рамках этого корня есть три элемента: страница 1, страница 2 и страница 4.
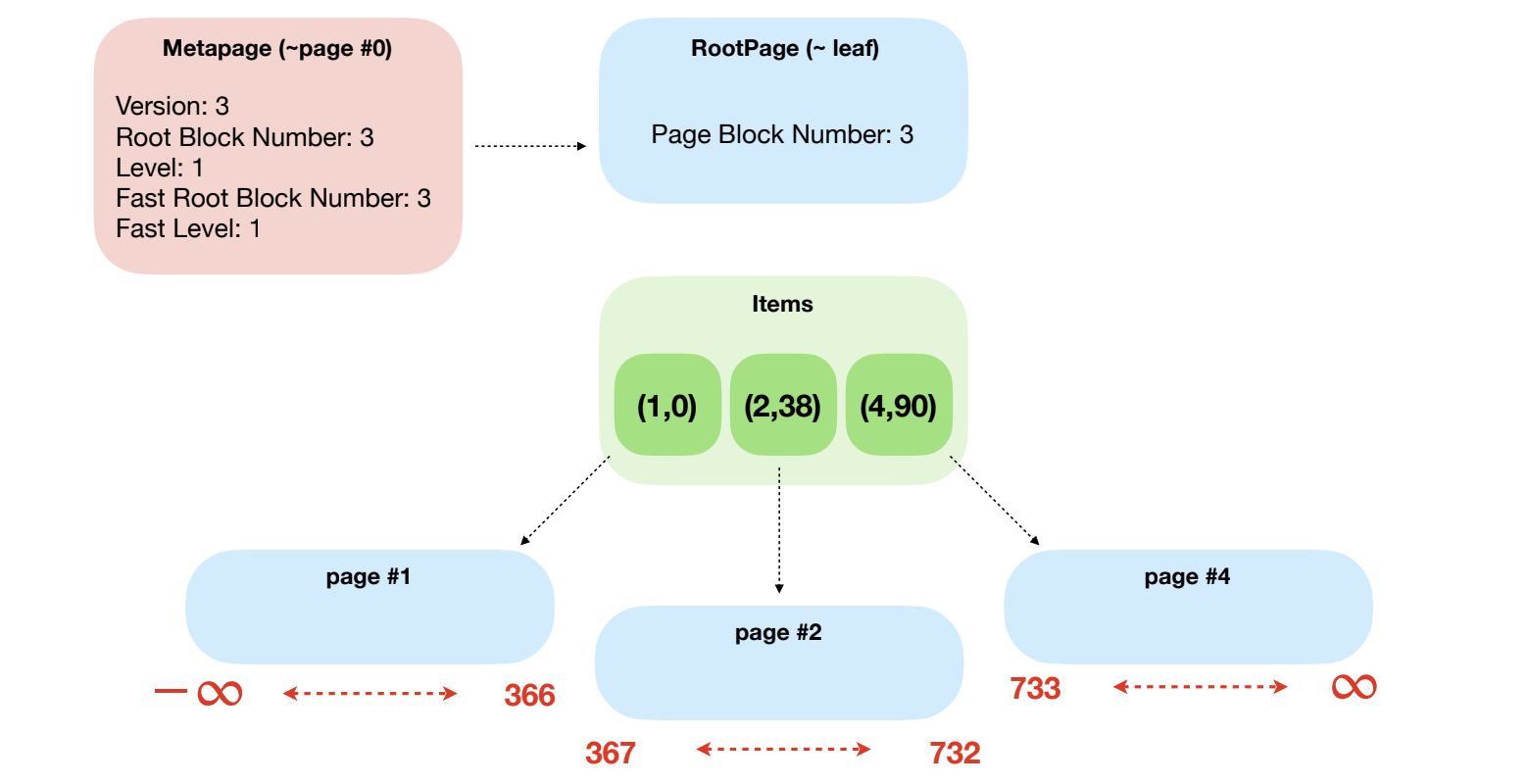
Страница #1 хранит по порядку все элементы, которые находятся слева до 366 включительно. Страница #2 начинается с элемента 367 и заканчивается границей в 732. Страница #4 содержит 733 и все последующие элементы до конца нашей таблицы. То есть у нас есть три страницы, которые хранят диапазоны.
Давайте заглянем в страницу #1, которая находится в самом левом порядке. Обратившись через статистику по странице bt_page_stat, мы получаем тип L, который означает лист в дереве. Также в статистике есть история по предыдущему листу и следующему листу — btpo_prev и btpo_next:

Ноль обозначает, что листа слева нет. Страница справа — это #2, она соответствует следующей странице по списку. В этом случае у нас перекидывается мостик: страница #1 знает, что страница #2 хранит следующий диапазон.
Если посмотреть на элементы, которые хранятся внутри конкретной страницы, то мы увидим перебор с единицы до 367 значений живых записей. Самая первая запись называется высшим ключом или high key. Он хранит границу: до какого элемента мы храним все остальные элементы. А сами индексированные данные начинаются со второго элемента после high key, это 2, 3, 4 и так далее до 367-й строки или до 366-го элемента. Сами элементы представлены как значения того типа данных, которые мы определили для таблицы user:

Дополним наш рисунок с логической топологией на основе той информации, которую только что получили. Страница #1 хранит элементы с единицы по 366, каждый элемент имеет свой адрес, который ссылается на data-файл, соответствующий таблице user, и у нас есть мостик-указатель от страницы #1 на страницу #2.

Со страницами #2 и #4 всё работает так же. Разве что у страницы #2 есть указание предыдущего листа и последующего, а у страницы #4 последующего листа нет и, соответственно, нет мостика-указателя на следующий элемент справа.
Нарисуем итоговую полноценную топологию. У нас есть:
Таблица на 1000 строк, индексированная по полю ID.
Метастраница #0.
Корень со страницей #3.
Элементы, которые являются промежуточными узлами с указателями на страницы: листья #1, #2, #4.
Cтраницы-листья, которые хранят те элементы, по которым мы делаем поиск с указанием адреса, куда нужно пойти, чтобы вычитать нужный элемент из диска.

То, что у нас получилось, — это не совсем дерево. Поскольку дерево по определению является является структурой, которая имеет корень, имеет промежуточные состояния в виде узлов и листья. Но если листья связаны между собой, то это не уже дерево. То, что мы видим — это ориентированный граф.
Для чего нужны мостики между листьями? Если вы используете выражение, например:
SELECT *
FROM user
WHERE ID = 1то можете чётко попасть в страницу #1 и найти элемент 1 на уровне data-файла, идя по адресу (0, 1) ctid. Но если у вас сценарий, когда вы делаете поиск из этой же таблицы, но с условием, что ID лежит между 10 и 100, например:
SELECT *
FROM user
WHERE ID BETWEEN 1 AND 100у вас получается диапазон или значения на сравнении. Чтобы постоянно не возвращаться в корень и не искать, где находятся следующие элементы. Для того, чтобы перебрать все листья, нужно перескакивать с одной страницы на другую. И как раз эти мостики-указатели дают оптимизатору понять, куда идти дальше. Да, вы можете пойти снова в корень и от корня понять, что на 366-м элементе закончилась страница один, а 367-й находится на странице #2, и начать опять сканирование по ней. Но эффективнее будет использовать указатели и переходить на следующие состояния, не возвращаясь в корень снова и снова.
Тем, кто хочет узнать больше, советую статью Лемана и Яо.
Синтаксис создания индексных B-Tree структур
Давайте рассмотрим примеры синтаксиса для создания тех или иных индексных структур.
Простой вариант выглядит так:
CREATE INDEX idx_user ON test.user (id) TABLESPACE ts_ssd;Если вы хотите, чтобы индекс содержался на быстрых дисках, то можете явно это указать, предварительно создав табличное пространство. В примере я назвал табличное пространство ts_ssd, то есть tablespace, который расположен на уровне SSD-диска, более быстрого, чем обычный HDD-диск.
Следующий тип индекса — уникальный, он создаётся командой:
CREATE UNIQUE INDEX idx_user ON test.user USING BTREE (id);Опция IF NOT EXISTS проверяет наличие индекса по имени. Достаточно совпадения по имени, но не по семантике индекса (по каким полям вы индексировали) поэтому будьте с этим внимательны:
CREATE INDEX IF NOT EXISTS idx_user ON test.user (id, name);Вы можете создать индекс, который будет упорядочен не по возрастанию, а по убыванию:
CREATE INDEX idx_user ON test.user (name DESC NULLS FIRST);Вы можете указать fill factor – это процент заполняемости страницы — для того, чтобы обеспечить оптимизацию по обновлению данных. Причём опции fill factor могут отличаться: одна одна таблицы, другая — для индекса.
CREATE INDEX idx_user ON test.user (name) WITH (FILLFACTOR = 70);CONCURRENTLY — очень важная опция. Создание индекса без неё производит блокировку данных на уровне таблицы, а это нежелательно. Опция CONCURRENTLY может создавать индекс параллельно с изменениями, которые поступают в таблицу. Минус этой команды в том, что индекс будет создаваться дольше, чем если вы её не применяете. Но поверьте, это намного эффективнее и лучше, чем заблокировать таблицу при создании индекса:
CREATE INDEX CONCURRENTLY idx_user ON test.user (id, name);Мы можем создать индекс с помощью ключевого слова ONLY. Команда помогает в случае с партицированными таблицами, когда вам нужно создать индекс только на одну конкретную таблицу, чтобы он не транслировался по всей топологии партицированных таблиц:
CREATE UNIQUE INDEX idx_user ON ONLY test.user (id);С удалением индекса — та же история про опцию CONCURRENTLY.
DROP INDEX CONCURRENTLY test.idx_user;Если индекс по каким-то причинам «сломался» (в рамках создания командой CONCURRENTLY, например), и нужно его пересоздать, поможет команда REINDEX. Она может пересоздать как конкретный индекс, так все индексы таблицы, схемы, базы данных и всех баз данных системы:
REINDEX (VERBOSE) { INDEX | TABLE | SCHEMA | DATABASE | SYSTEM } nameФункциональный B-Tree индекс
Давайте рассмотрим другие типы индексов, и начнём с функциональных. Мы можем создать индекс на функции, и самое главное в этой функции то, что она должна быть неизменной (иммутабельной).
Что такое immutable или неизменная функция? Самое простое объяснение, что если 2 + 2 = 4, то эта формула должна работать днём и ночью, на Луне и на Марсе. Неизменяемость означает, что функция всегда возвращает один и тот же результат, который вы ожидаете. Вы даёте на вход какие-то значения, и чётко уверены, что на выходе должно быть значение, которое удовлетворяет правилам формирования, например, математической логике.
Пример создания функционального индекса:
CREATE INDEX idx_user ON test.user (UPPER(name));В этом случае UPPER делает перевод значения в верхний регистр. Если вы создаете функциональный индекс, надо понимать риски. Первый риск в том, что цена изменения данных будет более дорогой. Когда вы вносите изменения в данные, то будет не только синхронизация индекса с таблицей, ещё будет применяться функция.
Второй момент состоит в том, что когда вы создаёте функциональный индекс, то должны делать поиск, используя указанную функцию. В своём примере я должен искать по UPPER(name), иначе индекс просто не сработает:
SELECT *
FROM test.user
WHERE UPPER(name) = 'KATE'; Условный B-Tree индекс
Условный индекс невероятен. Он даёт возможность создать частично уникальный индекс не на всю таблицу, а на части строк.
Допустим, я создаю уникальный индекс на табличке user, но для идентификаторов, которые лежат в интервале от 0 до 100:
CREATE UNIQUE INDEX idx_user ON test.user (name)
WHERE id BETWEEN 0 AND 100;Я чётко уверен, что имена в этом интервале являются уникальными. В этом случае поисковый движок у меня должен соответствовать типу индекса. Например, я ищу по имени то, что соответствует полю, входящему в построение индекса, плюс ещё добавляю, что идентификатор должен лежать в границах, которые удовлетворяют этому условному индексу:
SELECT *
FROM test.user
WHERE name = 'KATE' AND
id BETWEEN 0 AND 100;Простой бизнес-сценарий, когда уникальный индекс сильно помогает — это общий справочник в базе данных, который содержит домены, так называемые подсправочники, и элементы этих доменов в одной таблице. Условный уникальный индекс означает, что вы можете указать уникальность на подсправочники. В этом случае у вас получается, что значения между подсправочниками могут быть равны. Но с точки зрения принадлежности к домену эти категории разные, и вам нужно внести консистентность на уровне создания условного индекса на ваших данных.
Включённый B-Tree индекс
Когда я начал рассматривать включённые индексы, у меня возник вопрос. В чём разница между следующими вариантами индекса?
CREATE INDEX idx_user ON test.user (id) INCLUDE (name);и
CREATE INDEX idx_user ON test.user (id, name);Давайте посмотрим детальнее. В примере ниже я использую многоколоночный индекс, который содержит два столбца — ID и name. Затем, делаю вставку данных INSERT и запрос по получению метастраницы для определения страницы корня индекса:
TRUNCATE TABLE test.user;
DROP INDEX test.idx_user;
CREATE INDEX idx_name ON test.user(id, name);
INSERT INTO test."user"
SELECT i, 'Row #'||i::VARCHAR
FROM generate_series(1,1000) AS k(i)
SELECT *
FROM bt_metap(‘test.idx_name');В корне мы увидим одно потрясающее значение, которое сразу расшифрует, каким образом используется индекс. Обратите внимание, что столбец data содержит длинную строку, которая стилизована в некий бинарный код:
SELECT *
FROM bt_page_items('test.idx_user', 3);
В начале у нас идёт ID, а потом он конкатенирует с бинарным соответствием name строки. Первые 8 байт хранят наше значение ID, следующие 16 байт хранят строку. В этом случае в корневых элементах у нас хранится две строки одновременно:

Если мы посмотрим то же состояние, опустившись в листья, то найдём абсолютно аналогичную историю:

У нас получается немного «пухлый» индекс, где на каждом уровне — в корне и в листьях — хранится конкатенация двух значений: ID и name. Это означает, что данный B-Tree индекс делает ровный порядок по атрибутам запроса.
Давайте теперь посмотрим на включённый индекс. Я делаю тот же тест, но создаю индекс в паттерне INCLUDE (name):
TRUNCATE TABLE test.user;
DROP INDEX test.idx_user;
CREATE INDEX idx_name ON test.user(id) INCLUDE (name);
INSERT INTO test."user"
SELECT i, 'Row #'||i::VARCHAR
FROM generate_series(1,1000) AS k(i)
SELECT *
FROM bt_metap(‘test.idx_name');Я перехожу в корень и вижу, что в нём отсутствует name. То есть предполагается, что include name не хранится ни в корне, ни в промежуточных узлах:
SELECT *
FROM bt_page_items(‘test.idx_user’, 3);

Include содержится непосредственно в листьях. Мы храним конкатенацию только в них:

Чтобы лучше понять применение многоколоночного и включённого индекса, посмотрим на другой пример. Сначала я напишу многоколоночный индекс, который содержит ID и name:
CREATE INDEX idx_name ON test.user(id, name); И дальше буду искать фамилию. Для этого подойдут два варианта поиска:
SELECT surname
FROM test.user
WHERE id = 1 AND name = 'Kate'или
SELECT surname
FROM test.user
WHERE id = 1Что происходит при выполнении таких запросов? Surname в индексе не употребляется, а значит, я захожу в файл с индексной структурой, прохожу по адресу, где id = 1, а name = ‘Kate’, и нахожу почтовый адрес, где эта строка находится на data-файле. Дальше иду в data-файл и только оттуда достаю фамилию.
Теперь создам включённый индекс и сделаю поиск с его помощью:
CREATE INDEX idx_name ON test.user(id,name) INCLUDE (surname);
SELECT surname
FROM test.user
WHERE id = 1В этом случае уже сам индекс содержит в себе фамилию, то есть мне не нужно ходить в другой файл, и вычитывать её оттуда. Это фишка в дизайне создания Include-индексов.
Возвращаясь к вопросу в начале этого раздела: первый вид сканирования называется просто index scan, сканирование по индексу, второй — index only scan, сканирование только по индексу. В этом и состоит отличие. В случае index only scan мы не ходим в data-файл, поскольку индекс дублирует нужную нам информацию. А значит, он может быть более выгодным для поиска.
Имейте в виду, что include-индекс нужно тестировать через бенчмарки и нагрузочные тесты с точки зрения вашего конкретного запроса. Но он реально бывает полезным, когда в рамках запроса надо достать какое-то конкретное поле без похода в таблицу.
Как создавать оптимальные индексы?
Для начинающих хочу показать, как выбирать порядок индекса и как понять, что он является оптимальным для вашего запроса и конкретного случая.
Допустим, у нас есть простая таблица из двух столбцов:
A |
type1 |
B |
type2 |
C |
type3 |
Если создать все возможные варианты индексов, получится 15 штук: (A), (B), (C), (A, B), (A, C), (B, A) и так далее. Напомню, что (A, B) ≠ (B, A), мы увидели это, когда разбирали пример с многоколоночным индексом. Комбинаторика подскажет, сколько индексов возможно создать.
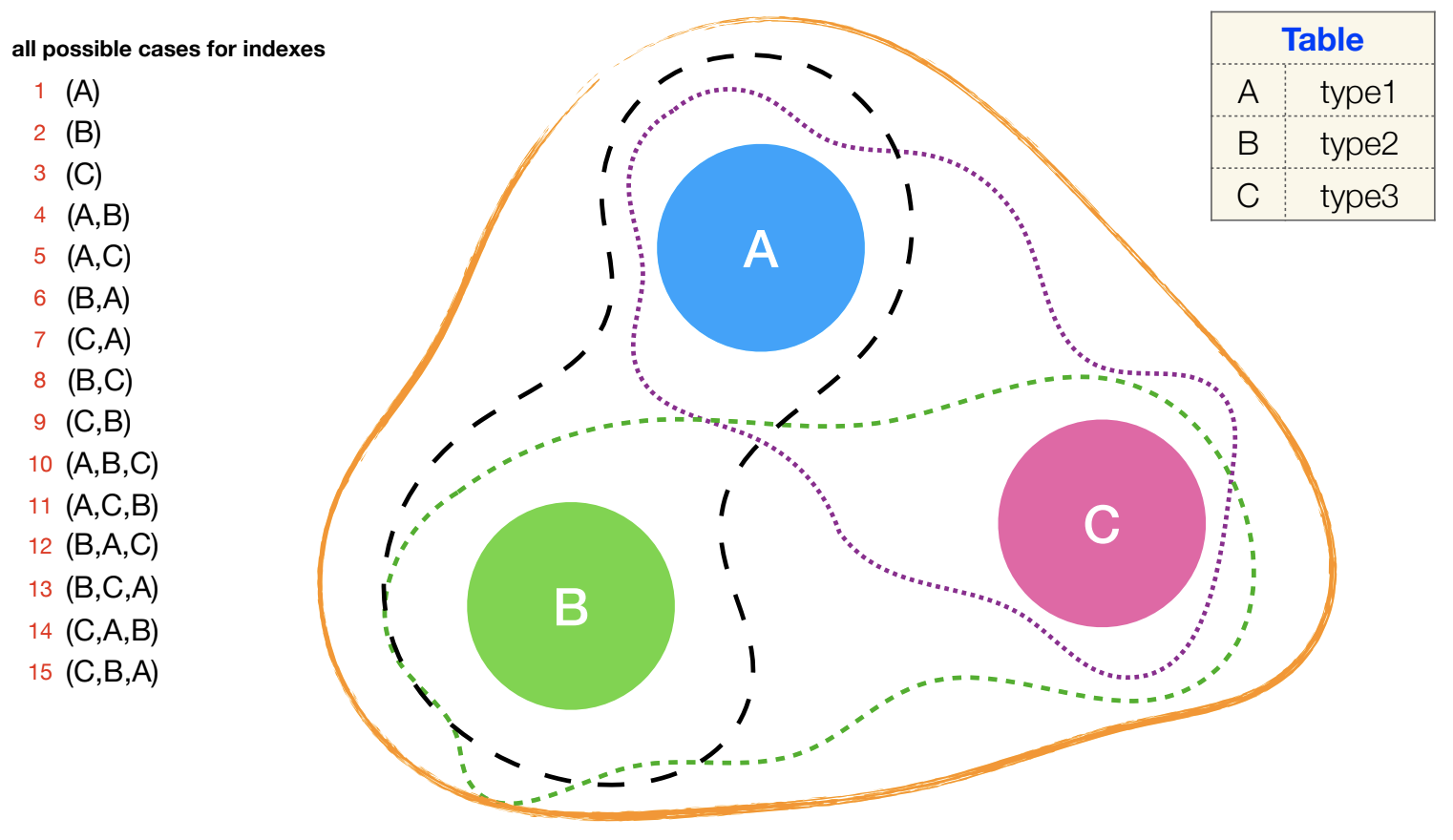
После того, как я создал индексы, надо проверить, как они работают. Для этого нужно сделать бенчмаркинг моего SQL-запроса. Через pg_bench я загоняю нагрузку на базу данных, и, когда нагрузка снижается, могу посмотреть через метаданные, каким образом используется индекс:
SELECT
relid::regclass AS table_name,
indexrelid::regclass AS index_name,
pg_size_pretty(pg_relation_size(indexrelid::regclass)) AS index_size,
idx_tup_read,
idx_tup_fetch,
idx_scan
FROM pg_stat_user_indexes JOIN pg_index USING (indexrelid)
WHERE idx_scan = 0 -- no index scans (means index is out of usage)
AND NOT indisunique -- non unique onlyВ результатах есть индекс с большим размером в 214 MB. В рамках теста он не использовался: не был прочитан, из него не было получения данных, индекс не был просканирован, везде нули.

Нужен ли нам индекс, который только занимает место? И даже мало того, что он занимает место на диске, возможно, он ещё прогрет и находится в памяти. Не удалить ли нам его? Мой ответ — нет. Не удаляйте такие индексы, предварительно не проверив один возможный и очень частый вариант. Дело в том, что иногда индексы используются редкими запросами.
Например, в конце года или месяца ваша бухгалтерия запускает отчёт, который должен сформироваться за секунды, перебирая все данные. И с индексом это работает быстро, а если вы удалите индекс, всё может стать плохо.
Поэтому если в рамках теста вы видите нули, то индекс становится только кандидатом на удаление. И дальше нужно проверить код и убедиться, что запрос, который существует в формировании дашбордов, отчётов, каких-то витрин данных, действительно не использует то условие, на основании которого построен индекс. Только тогда его можно будет удалить.
Семейства операторов для B-Tree индекса
В зависимости от сценария мы можем варьировать семейство операторов, с которыми работает наш индекс. Поэтому важно предварительно понимать, для каких целей вы создаёте индекс: возможно, не для общего ускорения, а для какого-то очень конкретного поиска.
Семейства операторов представлены в метаданных. Давайте посмотрим, какие есть для B-Tree индекса:
SELECT am.amname AS index_method,
opc.opcname AS opclass_name,
opf.opfname AS opfamily_name,
opc.opcintype::regtype AS indexed_type,
opc.opcdefault AS is_default
FROM pg_am am, pg_opclass opc, pg_opfamily opf
WHERE opc.opcmethod = am.oid AND
opc.opcfamily = opf.oid AND
am.amname = 'btree'
ORDER BY index_method, opclass_name, opfamily_name
Семейств операторов — огромное количество, практически по всем типам. Я для примера оставил integer_ops, text_ops и text_pattern_ops.
Когда вы создаёте просто индекс на столбце name, то предполагается, что это текстовое поле, и по умолчанию будет использоваться семейство операторов класса text_ops:
CREATE INDEX idx_username ON test.user (name text_ops);Если посмотреть в text_ops, то с ним вы можете работать только на равенства, на меньше, на больше, на меньше либо равно, больше либо равно. В этом случае вы можете искать значение строки, равное конкретному человеку, фамилии Иванов, или вы можете искать, какие значения больше Иванова по алфавиту, либо больше или равны по алфавиту:
SELECT am.amname AS index_method,
opf.opfname AS opfamily_name,
amop.amopopr::regoperator AS opfamily_operator
FROM pg_am am, pg_opfamily opf, pg_amop amop
WHERE opf.opfmethod = am.oid AND
amop.amopfamily = opf.oid AND
am.amname = 'btree' AND
opf.opfname = 'text_ops'
ORDER BY index_method, opfamily_name, opfamily_operator;
Если этих классов операторов вам не хватает, можно посмотреть на text_pattern_ops. Это другое семейство, которое содержит дополнительные операторы:

Тильды означают ничто иное, как операторы like. То есть вы можете искать по части текста, и этот индекс будет срабатывать.
Рассмотрим простой пример. Я создаю индекс на таблице, но указываю не класс по умолчанию для поиска по строке, а varchar_pattern_ops:
CREATE INDEX idx_username ON test.user (name varchar_pattern_ops);Дальше делаю EXPLAIN — это команда, которая выводит то, как работает ваш SQL в рамках базы данных, какие подтягиваются структуры, какие страницы, статистика и так далее:
EXPLAIN ANALYSE VERBOSE
SELECT name
FROM test.user
WHERE name LIKE 'иван%'В этом случае EXPLAIN показывает index only scan, то есть сканирование по индексу для поиска по LIKE. В ответе даже можно прочитать условие индексации, что значение имени должно быть больше либо равен «Иван», но меньше «Ивао». Мы не должны перейти на паттерн «Ивао», мы должны найти Ивановичей, Ивановых, но не должны найти Иваовых. В этом плане помогает индекс по LIKE.
Index Only Scan using idx_username on test."user" (cost=0.28..8.30 rows=1 width=13)
(actual time=0.013..0.013 rows=0 loops=1)
Output: name
Index Cond: (("user".name ~>=~ 'иван'::text) AND ("user".name ~<~ 'ивао'::text))
Filter: (("user".name)::text ~~ 'иван%'::text)
Heap Fetches: 0
Planning Time: 0.080 ms
Execution Time: 0.028 msРекомендации по книгам
Напоследок — привычные рекомендации по книгам:
“Database Internals” — Alex Petrov.
“Readings in Database Systems” — Peter Bailis, Joseph M. Hellerstein, Michael Stonebraker.
“PostgreSQL Notes for Professionals”.
“Understanding EXPLAIN”.
«Язык SQL. Базовый курс» — Е. П. Моргунов.
«Postgres изнутри» — Е. В. Рогов.
Последняя книга вышла в этом году. Она объёмная, но отлично показывает, как всё устроено и каким образом мы можем использовать оптимизацию тех или иных структур. Советую её посмотреть, как очень интересную.
В предыдущих сериях
Этот материал — часть серии, посвящённой Postgres. В прошлых статьях мы разбирали:

