Пока все оживлённо обсуждают прошлый пост - имеет ли право на Хабре публиковаться что-то смешное ( хотя и полностью реалистичное) на тему «инженерного чуда» - опубликую новую математическую задачу.

Убийство в “Восточном Экспрессе”. Версия для полиции.
В вагоне 14 мест, один пассажир потерял билет и выбирает купе случайным образом, другие 13 человек занимают свои места. Но если место занято, то пассажир выбирает другое свободное.
Последним в поезд входит Джонни Депп. Его хотят убить. Незнакомец (15ый пассажир) пробирается в вагон и протыкает того, кто спит в купе Джонни.
Какова вероятность, что это будет он, а не другой пассажир?
пассажир, потерявший билет, был СЛУЧАЙНЫМ
пассажир, потерявший билет, выбирает новое место в вагоне СЛУЧАЙНО
если своё место занято, то пассажир выбирает новое место СЛУЧАЙНО
Решение.
Задачу я придумала, опираясь на оригинал про безумную старушку и самолёт. Ее мне загадали однажды 2 программиста, когда я была совсем далека от программирования (привет Косте и Серёже).
Итак, я немного изменила условия, что повлияет на результат (если мои рассуждения верны). Но начало решения общее.
Пассажиры занимают свои места. Никаких других вариантов развития событий нет, пока в поезд не заходит пассажир без билета. Назовём его Пуаро.

Пуаро может:
занять своё место, тогда все займут места согласно билетам, а Джонни убьют.
занять место жертвы и тогда убьют Пуаро.
занять чьё-то ещё место.
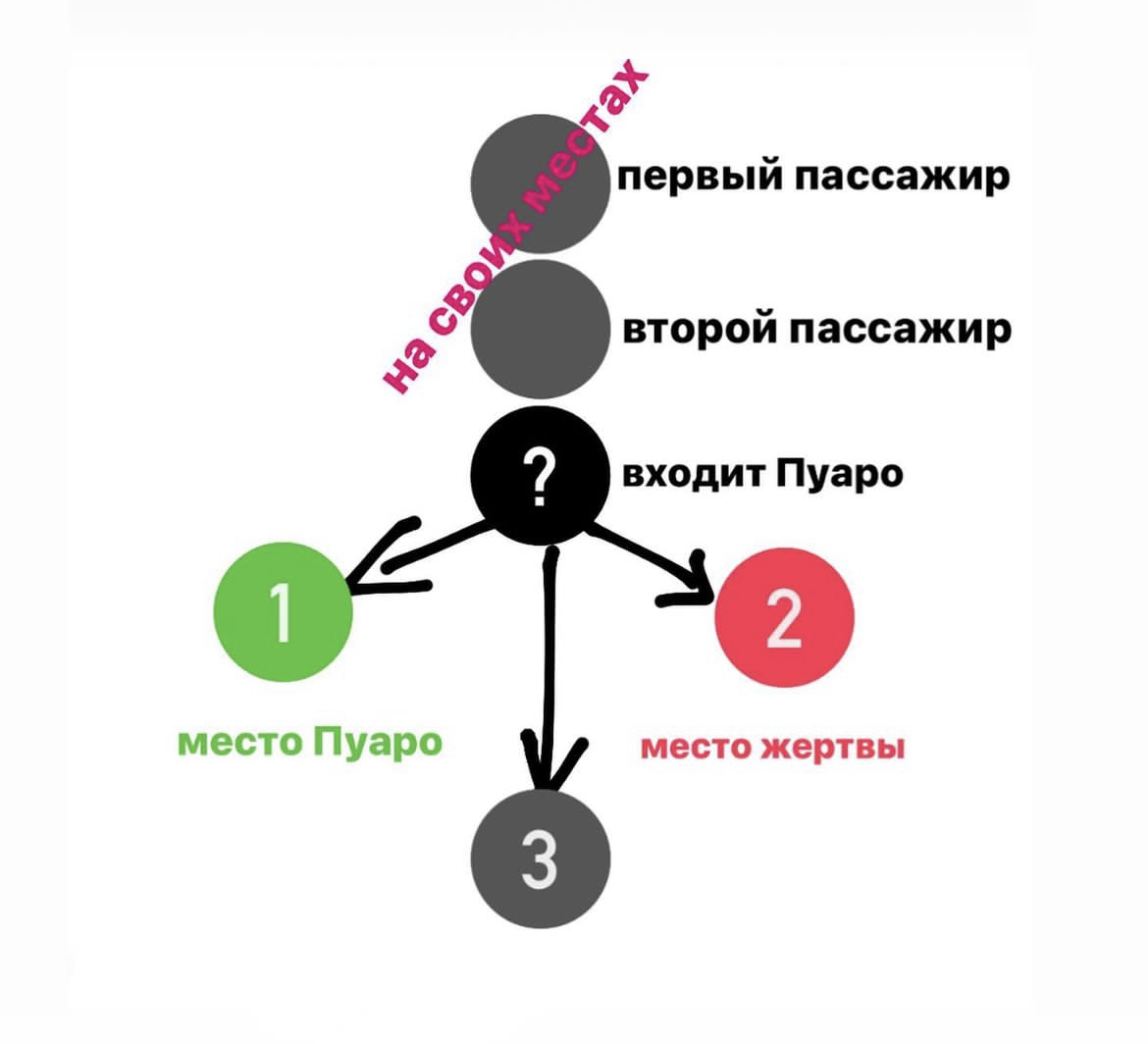
Следующий пассажир, чьё место занято, занимает:
место Пуаро.
место Джонни Деппа.
чьё-то чужое.
Вероятность (1) и (2) одинаковы. Вероятность (3) повыше, но это не важно, тк в случае (3) места Пуаро и жертвы остаются свободными, игра продолжается.

Если пассажир, на чьё место сели, займёт место Пуаро, порядок восстановится, оставшиеся пассажиры будут занимать свои места, и Джонни убьют.
Если пассажир, на чьё место сели, займёт место Джонни, убьют этого пассажира.
Предпоследний пассажир #13 (если до него никто так и не сел ни на место жертвы, ни на место Пуаро) выбирает одно из этих мест. И таким образом решает, кто умрет. 50 на 50.


Получается, что вероятность того, что на место Джонни Деппа сядет кто-то другой - 50%. Но пассажиром без билета может быть и сам Джонни (в 1 случае из 14). И тогда все остальные пассажиры занимают свои места, а его со 100% вероятностью убивают.
То есть в 13 из 14 случаев его убьют с вероятностью 50%. И в 1 из 14 - 100%.
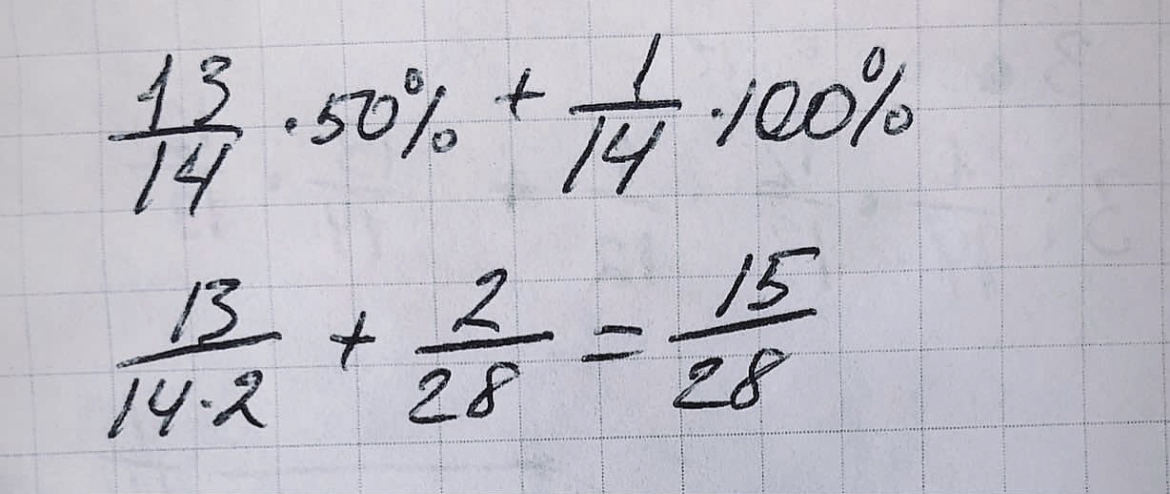
Вероятность Джонни быть убитым 15/28 или 54%.

Или я не права?
Комментарии (28)

Akela_wolf
11.11.2022 11:31+2Получается, что вероятность того, что на место Джонни Деппа сядет кто-то
другой - 50%. Но пассажиром без билета может быть и сам Джонни (в 1
случае из 14). И тогда все остальные пассажиры занимают свои места, а
его со 100% вероятностью убивают.В условии задачи этого не подразумевается. Условие задачи сформулировано так, что заходят 13 пассажиров, которые могут перемешаться. А могут и не перемешаться. И тогда Джонни займет или свое место или не свое.
На мой взгляд, интереснее было бы решать задачу, когда пассажиры прибывают в случайном порядке, один из них потерял билет, один из них Джонни Депп. И два случая - у Деппа билет всегда при себе (известно что он его не потерял), либо Депп тоже может оказаться "растеряшей".
Во втором случае добавляется вероятность 1/14 что Депп - "растеряша" и тогда все зависит от того которым по счету он заходит в вагон и, сооответственно, с какой вероятностью занимает свое (или не свое) место.
Ну и тут приходится рассматривать два принципиально разных случая - Депп зашел в вагон до "растеряши" или после. Если до - то он умирает 100%. Если после - то с каким шансом его место уже занято.

Galamaly Автор
11.11.2022 11:42+1Прямо вижу цикл в цикле)) Интересно, надо составить несколько вариантов этой задачи. Чтобы окончательно запутать тех, кто просто хочет подсмотреть ответ в готовых решениях.

dyadyaSerezha
11.11.2022 11:42+5Крайне мутные начальные условия. Первые же рассуждения дальше показывают, что я что-то не знал, а оно подразумевалось. Дальше читать не стал - надо было угадать настоящие условия задачи.

Galamaly Автор
11.11.2022 11:45-5Ну это дизлайк. «Я не понял, дальше читать не стал. Фи!»
Муть начальных условий в том, что пассажир без билета может быть Джонни, а может и не быть. И нужно посчитать исход в каждом случае отдельно. Потом найти вероятность того, что Джонни - это и есть тот, кто потерял билет. И перемножить. Потом сложить.
Это не муть. Это вариативность и теория вероятности.

dopusteam
12.11.2022 08:13+2На самом деле, можно и прислушаться. Задача изначально сформулирована так, что многие вещи приходится додумывать.
Не знаю, почему сложно адекватно отреагировать и поправить.

Galamaly Автор
12.11.2022 10:15-1Потому что поправки формата :
пассажир, потерявший билет, был СЛУЧАЙНЫМ
пассажир, потерявший билет, выбирает новое место в вагоне СЛУЧАЙНО
если своё место занято, то пассажир выбирает новое место СЛУЧАЙНО
Но ведь это и так понятно. Всё случайно. Надо посчитать вероятность.
Но я вас услышала. Давайте добавлю

MUTbKA98
11.11.2022 11:59+1Если "потеряшка" занял чье-то место, то это эквивалентно тому, что токен "потеряшка" получает вошедший. Итого все сводится к тому, что ДД заходит в вагон либо со своим собственным токеном, либо забирает токен у предпоследнего вошедшего.

Akela_wolf
11.11.2022 12:07Не понял вашу мысль. Токен "потеряшка" получает тот у кого билет на то место, которое занял "потеряшка". Таким образом, у нас возможна цепочка из 14 потеряшек (первый потеряшка заходит первым и далее все занимают места друг друга, последний - место первого потеряшки) или из единственного потеряшки (который заходит последним и занимает единственное свободное - его - место). И все промежуточные варианты.

Galamaly Автор
11.11.2022 12:23Всё верно. Токен «потеряшка» может передаваться от одного к другому. Но сводится все к финалу, когда заходит Джонни Депп. И либо у него свое место, когда предыдущий пассажир с токеном «потеряшка» вдруг занимает место другого пассажира , либо его место уже заняли и ему придётся пересесть и выжить.

Akela_wolf
11.11.2022 12:33+1Именно. По большому счету, задача сводится к двум случаям:
Заходит Депп с билетом. С какой вероятностью его место свободно (= умрет)?
Заходит Депп без билета. Сколько осталось свободных мест (= вероятность сесть на свое и умереть)?

Galamaly Автор
11.11.2022 12:36+1Во втором случае (Депп без билета) его 100% убьют. Так как он входит последним (в условии задачи). А до этого у всех пассажиров были билеты (тк у нас только 1 пассажир потерял билет), и они занимали строго свои места.

Mingun
12.11.2022 09:21+2Всё-таки Пуаро-не-Дэвид-Суше не воспринимается, как Пуаро. Сначала даже не понял, кто это на КДПВ изображён… А потом-то как дошло!


mayorovp
Чтобы выше решение стало верным, нужно внести в условие несколько дополнений:
И если равновероятность ещё можно "додумать", поскольку это в таких задачах условие по умолчанию, то вот тот факт, что забывчивый пассажир — случаен, в условии важен.
Без упоминания случайности забывчивого пассажира правильный ответ на задачу будет таким:
50% если забывчивый пассажир не последний
100% если забывчивый пассажир последний.
Galamaly Автор
И всё же 54%, если это условие опущено)
Нужно предусмотреть вероятность того, каким по счету окажется забывчивый пассажир.
В 13/14 случаев непоследним. В 1/14 последним.
А дальше перемножаем-складываем.
mayorovp
Вот как раз если условие случайности пассажира опущено — никаких 54% и не получается.
Galamaly Автор
Опущено условие, кто потерял билет. Всего 14 пассажиров.
1/14 вероятность того, что потерял Джонни Депп (последний пассажир, место которого приговорено к смерти).
13/14 - вероятность того, что это не Депп.
mayorovp
Если не указано, что билет потерял случайный пассажир — вы не можете предполагать эти вероятности. Нет оснований. Можно только решить для всех вариантов и остановиться на этом.
Galamaly Автор
Есть условие - 1 пассажир потерял билет. Дальше считаем: 1/14 что это Джонни потерял. 13/14 - что не Джонни. Почему я не могу предполагать такую вероятность?
Кто-то из 14 потерял билет. Вероятность 1/14, что это Джонни.
mayorovp
Потому что это рассуждения из той же серии, что и про вероятность встретить динозавра на улице.
Galamaly Автор
В условии указано - 1 из 14 пассажиров потерял билет.
Вы действительно считаете, что это совсем не равнозначно «случайный человек из 14 пассажиров потерял билет».
Нет слова «случай», и сразу появляются динозавры?
mayorovp
Разумеется.
Galamaly Автор
Мне бы вашу уверенность по жизни
vesper-bot
Последним у нас ДД, и ваш ответ переформулируется в «50% если билет забыл не ДД, 100% если ДД». Что в принципе соответствует промежуточному результату в статье.
Galamaly Автор
Ура! Меня поняли и услышали! Если под «промежуточным» результатом подразумевается 15/28
mayorovp
Именно так, без уточнения условия правильным является промежуточный ответ из поста, а не окончательный.
Galamaly Автор
Что вы подразумеваете под промежуточным и окончательным ответом?
54% - как сумма возможности происшествия события в 2 сценариях: когда Джонни потерял билет ( 1/14*100%) и когда потерял не он (13/14*50%).