Задачи про рыцарей и лжецов - это классические математические задачи на комбинаторику.
Жили-были на одном небольшом островке в океане два племени — рыцари и лжецы. Рыцари были настолько горды и благородны, что не могли говорить ничего, кроме правды, правды и только правды. А лжецы не различали истину и вымысел.

На острове живут 50 человек. Из которых 35 - лжецы, 15 - рыцари. Какое наименьшее количество человек нужно выбрать, чтобы спросив потом у каждого, кто именно лжецы, по ответам вычислить хотя бы 1 лжеца?
Сразу поясню, что все жители острова знают, кто есть кто. И что отобрать людей для опроса нужно сразу, а не в зависимости от ответов, которые они дают.
Теперь начинаем рассуждать.
Когда мы спрашиваем жителя, кто рыцари, а кто лжецы, он указывает на 15 потенциальных рыцарей и 35 лжецов. Если спросить того, кого он назвал рыцарем, кто есть кто. То возможны 2 варианта:
второй человек подтверждает версию первого (назовем их Команда 1)
или его показания не сходятся с 1, а тогда значит, что врет либо второй (но первый назвал его рыцарем, а значит тоже соврал), либо первый. В любом случае мы идентифицируем 1 лжеца (первый). Ч и тд.
Допустим мы опросили 15 первых человек и все они - Команда 1. То есть абсолютно идентично называют себя рыцарями, а остальных - лжецами. Дает ли это право сказать, что мы решили задачу?
Не совсем. Они все могут оказаться лжецами, которые сговорились.
Теперь предположим что опросили 31 человека. Сепарировались Команда 1 (зеленые), Команда 2 (красные) и у нас 31-ый синий игрок, который называет рыцарем себя, а предыдущих 30 - лжецами. Кому довериться?

Могут быть правы, как первые, так и вторые, и даже 31-ый.
Опросим еще 5 человек. Если кто-то из новеньких 5 назовет рыцарями кого-то из красных или зеленых, то мы автоматически найдем 1 лжеца (тк красные и зеленые называют рыцарями только себя, а остальных - лжецами, а значит не может кто-то из 5 новеньких назвать рыцарем красно-зеленых).
Итак, все новенькие 5 называют рыцарями - синих.
Опросим 46 человек. И у нас будет 3 команды по 15 (зеленые, красные, синие) и 1 человек, который вроде как должен решить, кто же тут прав. Все 45 человек называли этого 46-го лжецом, значит он лжец, тк не собрал на свою сторону 15 человек.
А теперь развернемся. Вспомним, что ищем не того, кто прав. А ищем хотя бы одного лжеца. А значит, можно было остановить поиск намного раньше. Вот у нас 30 человек (красных и зеленых), которые ополчились друг против друга. Вот у нас 31-ый синий. Должно получиться, что все 3 команды обзывают коричневых - лжецами. А коричневым будем не с кем объединиться, чтобы назвать своих 15 человек - рыцарями.
Но вдруг мы опросим еще 5 синих человек и выяснится, что первые 5 синих - говорят одно, а шестой синий назвался желтым и сказал, что все люди до него - врали.
Зеленые, красные, синие или жёлтые? Кто врет и где наш лжец?
Отгадка - в переметнувшемся синем. Остальные 5 синих назвали его своим, а он их предал, что означает, что синие - точно не рыцари. Иначе бы они знали, что переметнувшийся - лжец. И не называли бы его рыцарем. Мы всё еще не знаем, кто рыцарь - зеленые, красные или желтые, но синие - точно врут.
Вроде решили. Вот и я так подумала и отправила ответ.
Но нет.
Важным и ложным допущением было то, что мы делили группы на15 человек. А могло же быть по-другому. Команда 1 - 11 человек, команда 2 - 11, команда 3 - 11. итого 33 человека. Которые называют рыцарями себя и еще четверых, которые не вошли в первоначальную выборку для допроса.
Потом берем еще 11 человек - и они делают тоже самое (желтые).

Из оставшихся 6 коричневых есть 4 - которых все называют рыцарями. Кто врет - неизвестно. Продолжаем опрос.
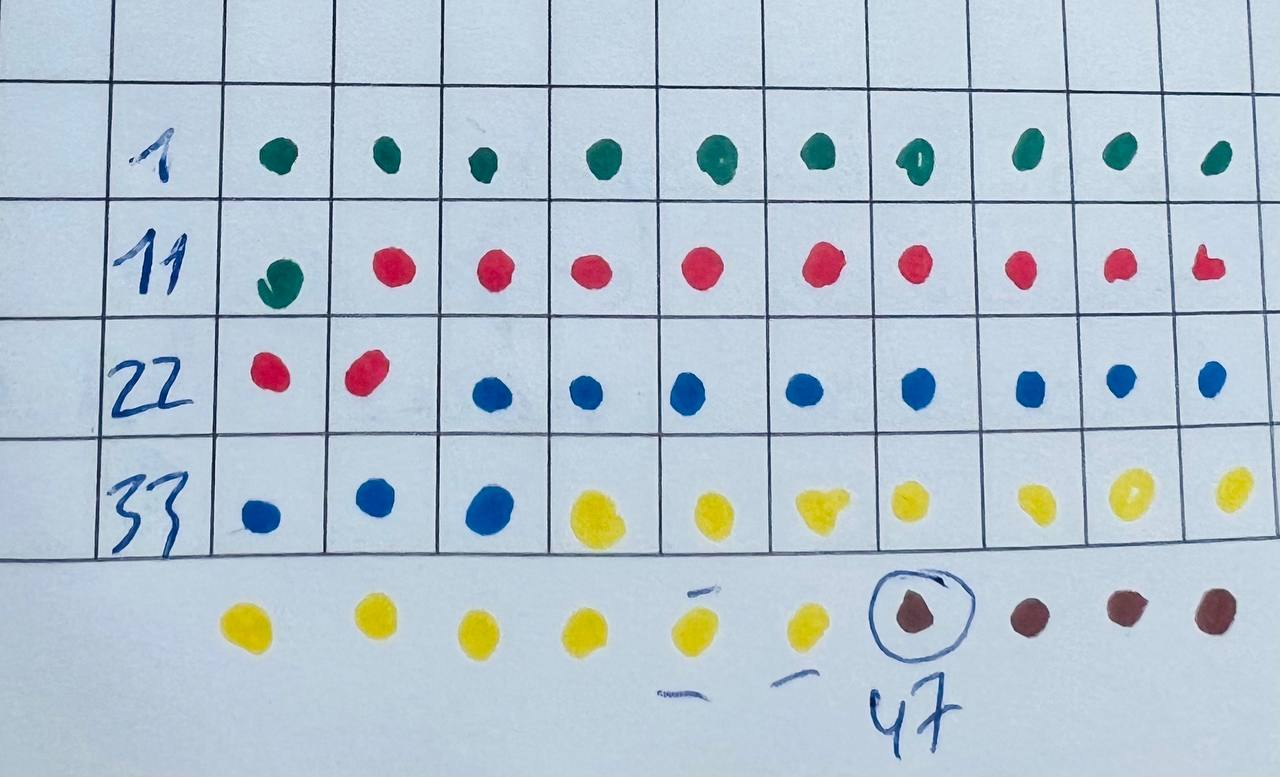
Берем еще 2 человека. Они должны будут присоединиться к одной из 4 фракций (зеленые, красные, синие, желтые). Допустим они выбрали желтых.
Тогда достаточно будет спросить 47 человека, которого все называют рыцарем (коричневый) и мы узнаем, где лжец. Даже сразу, где все лжецы. Тк 47ой человек - точно рыцарь.
Бонусом: немного другое толкование изначальных условий могло быть дать куда более интересное решение. Если бы можно было опрашивать островитян по очереди. То достаточно было бы спросить у пятерых, кто есть кто, и найти лжеца. То есть первый показывает на 15 рыцарей и 35 лжецов. Идем к лжецу. Он указывает 15 своих рыцарей и обзывает лжецом первого и тд.
Но нет, нужно сразу взять рандомных людей и потом их опрашивать.
Также существуют целые классы задач того же типа, но с другими персонажами — задачи о пациентах и врачах, собранные в частности в книгах математика Рэймонда М. Смаллиана.
UPD
К сожалению, решение не поняли и принялись «с размаху» критиковать. Очень жаль.
Добавлю другое описание решения из учебника. Может быть сумею достучаться.

Комментарии (71)

Mirzapch
09.12.2022 16:27+19А лжецы не различали истину и вымысел.
В классических задачах на логику лжец лжёт всегда. В вашей формулировке ответы (высказывания) лжеца будут подобны генератору псевдослучайных чисел. На таких ответах решение задачи не построить.

Galamaly Автор
09.12.2022 16:29-5Задачи про лжецов и рыцарей могут иметь разную формулировку. Лжецы не обязаны всегда врать. Решите задачу с такими условиями. Не можете? Посмотрите решение ниже. Что с вами не так?

Mirzapch
09.12.2022 16:34+11"Не обязаны" и "не понимают что творят" - сильно разные ситуации. Опять же, в классической школе те кто "не обязаны", и могут врать в зависимости от ситуации называются "хитрецами".

Galamaly Автор
09.12.2022 16:36-11Я взяла формулировку задачи из Тинькофф. Решение - мое. Ответ - проверен Тинькофф. Ваши претензии про "хитрецов" и "лжецов" (которые всегда обязаны врать) - немного странные.
Лжецы, которые ВСЕГДА врут - какие-то лжецы в вакууме.
holodoz
09.12.2022 16:44+14То есть вакуумные рыцари - это ок, а лжецы - нет? Я как раз зашёл написать про то, что решал задачу про 100% правдивых людей и людей, которые абсолютно рандомно врут. А потом выясняется, что они могут сговариваться, т.е. рандома нет. Поставьте задачу точно, чтобы был смысл читать ваше решение и сравнивать со своим.

Galamaly Автор
09.12.2022 16:53-12Рыцари, которые всегда говорят правду - это норм. Почему нет? Честные. Лжецы, которые всегда врут - немного странно. Тк задавая им ответ с 2 вариантами ответа, всегда можно узнать истину, что странно.
Могут сговариваться - это оборот для объяснения решения. Ваша задача - взять столько рандомных людей, чтобы можно было ТОЧНО найти ХОТЯ БЫ ОДНОГО лжеца.
Сговариваются ли при этом кто-то или случайно повторяет расстановку за другим - вообще не важно.
Как-то поглупел ХАБР. Что с вами, ребят?
holodoz
09.12.2022 17:26+10У меня такая задача. На острове есть один рыцарь в сияющих доспехах и толпа глуповатых аборигенов. Сколько аборигенов нужно опросить, чтобы убедиться в том, что задача поставлена некорректно?

Galamaly Автор
09.12.2022 17:34-6К счастью, рядом с рыцарем стоит Пентиум "Тинькофф", который и придумал задачу, а потом проверил решение.

SteamEngine
09.12.2022 17:41+12Но это никак не отменяет дурной формулировки задачи. Тинькофф придумал задачу, в которой, казалось бы, используются классические формулировки, но на самом деле нет. Что ж теперь, от того, что это Тинькофф, стало лучше?

Galamaly Автор
10.12.2022 11:04"Дурная" здесь не формулировка, а чья-то голова. Прочитайте ВНИМАТЕЛЬНО условия, решение и закрепленные комментарии. Классический Лжец всегда врет? Ок, я сразу написала в условии, что мои лжецы то врут, то не врут. И при этом задача все равно отлично решается.

leok
09.12.2022 19:30+1Не знаю ни одного человека, который всегда говорит правду. Ни разу это не норм.

StjarnornasFred
10.12.2022 00:06+2Рыцари, которые всегда говорят правду - это норм. Почему нет? Честные. Лжецы, которые всегда врут - немного странно.
В задачах про рыцарей и лжецов не требуется приводить какой-то реалистичный обоснуй - его там априори нет. Это абстрактные персонажи, которые по условию всегда говорят либо только правду, либо только ложь. Про тех, кто иногда лжёт, я не слышал, но предположу, что их называют ловкачами или трикстерами. Ну или хитрецами, как выше предложили.

adeshere
09.12.2022 21:06+4... и людей, которые абсолютно рандомно врут. А потом выясняется, что они могут сговариваться, т.е. рандома нет. Поставьте задачу точно, чтобы был смысл читать ваше решение и сравнивать со своим.
Строго говоря, если Вы решили задачу про людей, которые врут рандомно, то это решение вполне применимо и к тому случаю, когда хитрецы (лжецы) могут сговориться. Так как тот набор ответов, который дали сговорившиеся лжецы (хитрецы), всегда может с некоторой вероятностью получиться и у случайно врущей команды. А мы ведь ищем гарантированное решение, а не то, которые будет правильным с некоторой вероятностью?
Но согласен, что задача про лжецов, которые врут всегда, заметно проще, чем про рандомных.

Mirzapch
09.12.2022 16:51+3Допустим... Что T что-то проверил.
Поясните, как могут "сговориться" те, кто не отличает истину от лжи? Согласно постановке задачи, их высказывания (утверждения, суждения) от сговора зависеть не могут.

Galamaly Автор
09.12.2022 17:08Представьте: отобрали вас и еще 10 человек. Спрашивают, кто свои (всего их 15), кто шпионы (всего их 35). Ваш сосед говорит всем, что вы - хороший. А вон те 35 - плохие. Потом наступает ваша очередь. Вы понятия не имеете, где кто. Но "сговорившись" вы повторите версию первого, ведь он назвал вас СВОИМ.

vassabi
09.12.2022 17:21А лжецы не различали истину и вымысел.
то есть если лжеца спросить "ты лжец", то он может ответить как "да", так и "нет" ?
и - дальше - по комбинаторике- если если его спрашивать 10 раз, то вероятность получить от него 10 "да" равна 2**-10, а 5 "да" - равна 2**-2 , правильно ?

Galamaly Автор
09.12.2022 19:21+4Если скажет «да», значит точно лжец и задача решена. Но это самый простой случай. Нам же нужно найти лжеца гарантировано. То есть рассматриваем самый сложный случай.

adeshere
09.12.2022 20:54Лжецы, которые ВСЕГДА врут - какие-то лжецы в вакууме.
Что значит "какие-то"? Есть же классическое определение: сферические лжецы в вакууме.
;-)

SuperTEHb
09.12.2022 16:43+4Так-то в начале задачи эти термины оговорены, так что претензия несколько мимо. Но что формулировка неоднозначная, тут согласен. Воспринимал постановку задачи несколько неверно, пока не начал читать предлагаемое решение.

Galamaly Автор
09.12.2022 16:59-4Что значит неоднозначная? Где расхождение? Про "сговариваться" объяснила выше. Представляйте, что никто не сговаривается, а случайно повторяет слова предыдущего оратора.
Если не повторяет - задача решится просто. Про это тоже есть в решении.
SuperTEHb
09.12.2022 18:15+2Что ж, давайте углубимся. Касаемо неоднозначности смутил вот такой момент
Какое наименьшее количество человек нужно выбрать, чтобы спросив потом у каждого, кто именно лжецы,
Лично я подумал, что требуется определить кто из них кто среди выбранной группы, а по тексту далее стало понятно, что речь о всём острове. Так-то мелочь, но меняет понимание задачи.

adeshere
09.12.2022 21:26+2Что значит неоднозначная? Где расхождение? Про "сговариваться" объяснила выше. Представляйте, что никто не сговаривается, а случайно повторяет слова предыдущего оратора.
Мне кажется, Вы в горячке спора ушли в частность. Пример с "повторением" - совершенно излишний, так как рандомно врущие лжецы/хитрецы потенциально могут выдать абсолютно любой набор ответов. В том числе и тот, который выглядит так, как будто хитрецы сговорились. Да, вероятность этого небольшая, но она конечная (разумеется, если число жителей острова конечно - но нам сообщили, что это так). А мы же решаем математическую задачу. Значит, нас устроит только
гарантированное решение
хохмы ради, в современной математике (кажется, в теории чисел, но ссылку сейчас не смог быстро найти) иногда встречаются такие патологические случаи, когда просто доказать гипотезу невозможно, но можно доказать, что она верна с вероятностью единица
Разумеется, когда каждый вопрос допускает n вариантов ответа, а мы опросили m человек, то при рандомно врущих хитрецах/лжецах вероятность получения какого-то конкретного набора будет обратна m в степени n. То есть, даже на сравнительно небольших островах вероятность может оказаться исчезающе малой. В практической жизни иногда можно такими вероятностями пренебречь... а вот на собеседовании - не факт...

GospodinKolhoznik
10.12.2022 10:37+3Так это делает задачу сложнее. В классических задачах лжецы это такие же рыцари, которые всегда говорят правду, только у них встроен инвертор меняющий да на нет. Что очень далеко от лжецов из настоящего мира, которые говорят много правды, когда им нет разницы что говорить, а лгут только тогда, когда им это выгодно.

ksbes
09.12.2022 17:18+4По-моему как-то неправильно. Ведь мы можем опрашивать мнение не только о коммандах, но вообще обо всех жителях, в том числе и о нём самом.
Т.е. мы на каждого жителя можем составить «досье» из N ответов, где N — отобранное нами количество жителей.
Далее замечаем, что у 15 рыцарей в досье будет всегда будет не менее KN<N (<=) отметок «рыцарь», где KN — отобранных нами рыцарей. А лжецов не менее N-KN отметок, что они лжецы
Если лжецы намеренно портят нам жизнь, выравнивая оценки, то они не смогут этого сделать только, если KN > N — KN, что может случиться только случайно. Причем при N > 31 лжецы гарантированно смогут нас запутать (т.к. их гарантированно будет больше рыцарей).
Задавая меньше вопросов мы лишь ухудшим ситуацию, т.к. получим меньше информации.
Иными словами гарантированно найти лжеца — нельзя.
но если:
1) лжецы лгут всегда:
Достаточно 1 человека. Так по распределнеию рыцарей/лжецов по его мнению в деревне мы всегда скажем лжец он сам или нет.
2)лжецы лгут рандомно, с вероятностью 1/2 говорят правду, с вероятностью 1/2 говорят ложь:
Тут нет гарантии (т.к. в худшем случае будет такое же распределение, как у «злонамеренных» лжецов). Но если говорить о высокой вероятности определения лжеца, то мы можем построить распределение ответов. В среднем у каждого рыцаря получится KN + (N-KN)/2 +- sqrt(N-KN) меток рыцаря, а у лжецов (N-KN)/2 +- sqrt(N-KN). Вычитаем, получаем что между лжецом и рыцарем в среднем разница будет КN +-2sqrt(N-KN). В худшем случае у нас будет KN=N-15 рыцарей. Получаем уравнение N-15 > 2sqrt(15) (* множитель уверенности, там 3, 5 «сигма», но я возьму 1). Получаем N > 23
Но вообще задача сформулированна некорректно.
Хотя бы условие, что нельзя выбирать по предыдущим ответам — оно просто глупо, что автор нам прекрасно продемонстрировал(а) просто проэмулировав этот выбор среди уже как бы выбранных.
Galamaly Автор
09.12.2022 17:25-9Гарантированно найти лжеца, отобрав 47 островитян - МОЖНО. Решение внутри поста. Оно верное, проверено Тинькофф. Ваши рассуждения ложны в части того, что вы считаете только отметки "рыцарь" и "лжец", а надо рассматривать систему - сколько людей и из какой группировки так говорят.
Задача сформулирована КОРРЕКТНО. Примите и решите. Не можете решить - изучите чужое решение.
ksbes
09.12.2022 17:35+151)Мне глубоко наплевать с высокой колокольни на Тинкофф. Пусть принимают что хотят, но авторитет — не аргумент.
2) Математика — не церковь. Решения не принимают, а либо подтверждают, либо опровергают. Я сделал последнее, строго доказав отсутствие решения в случае «рандомных» лжецов. Вы же в свою очередь можете либо подтвердить моё опреовержение, либо опровергнуть его столь же строго математически, не взывая к сомнительным авторитетам.
В чём конкрентно в вашем решении ошибка мне искать лень. Я просто доказал что она там имеется. Да в математике и логике так можно. А вот полагаться на чужое мнение — нет.
Galamaly Автор
09.12.2022 17:47Вы не слушаете аргументы. Я написала, в чем вы не правы. Нельзя просто считать отметки "рыцарь" и "не рыцарь" - это не приведет к ответу. Предложенный вами метод решения задачи - не даст ответ. Но это не означает, что нет других методов. В статье как раз мой метод решения задачи.
Добавлю еще один метод, предложенный другим участником (прямо в статью в конце).

Kriminalist
09.12.2022 18:03а где в условии есть упоминание, что опрашиваемые знают ответы других? Я бы предполагал формат опроса в виде тайного голосования, список жителей, и надо поставить галочки на лжецах.

adeshere
09.12.2022 23:34+4Задача сформулирована КОРРЕКТНО. Примите и решите. Не можете решить - изучите чужое решение.
1. Даже если задача сформулирована корректно, отсюда совершенно не вытекает, что предложенное автором решение - правильное. Как совершенно справедливо заметил @ksbes, истина в математике ищется не отсылкой к авторитетам, а хорошо аргументированным, логически цельным рассуждением. Даже если Вы очень-очень доверяте Х, это не значит, что предложенное им решение всегда безупречно. Поэтому если Вы не согласны с рассуждениями @ksbes, опровергающими Ваше решение, то укажите на ошибку в них.
2. Я сам тоже не знаю истину. Но приведенные в статье рассуждения действительно выглядят очень слабо и совершенно не убеждают. А разбиение отвечающих на "команды" в зависимости от из первого ответа - это вообще за гранью добра и зла. Тем более, что в условии об этом (разрешен ли повторный опрос) вообще нет ни слова.
3. Если бы эту задачу решал я, то начал бы с самого простого крайнего случая. Допустим, что мы можем опросить всех жителей города многократно. (Запрет повторных опросов только ухудшает ситуацию, так как количество полученной нами информации в этом случае уменьшается. Поэтому если решения нет при разрешенных многократных опросах, то его нет вообще). Допустим также для начала, что на острове есть всего лишь один житель.
Итак, у нас есть один человек, мы можем задать ему любое число вопросов (но конечное! - если верить вот этому, то вряд ли получится подняться выше 10^10 да-нет). Надо определить, рыцарь он, или хитрец.
Я утверждаю, что в этом случае ответ - нет, не можем.
Так как хитрец может случайно отвечать на все вопросы точно так же, как отвечал бы на его месте рыцарь. Вероятность этого маленькая, но не нулевая. Поэтому если в задаче присутствует хитрец, а не лжец, то мы в принципе не сможем отличить его от рыцаря со стопроцентной гарантией.
Добавляя в задачу других рыцарей и хитрецов, мы никак эту ситуацию не изменим. Любое числе хитрецов может случайно отвечать на все вопросы, как рыцари. Вероятность этого маленькая, но не нулевая. А если они сговорятся, то эта вероятность может еще и значительно вырасти...
Поэтому и перекрестный опрос тоже не поможет. Ведь в общем случае мы изначально не имеем гарантий, что хоть кто-то из опрашиваемых - рыцарь. Что бы он ни отвечал, хитрец потенциально может дать точно такие же ответы на любые заданные ему вопросы.
Итого у меня получается, что в общем случае задача с хитрецами неразрешима в принципе, если у нас нет какой-то дополнительной информации, которая бы существенно помогла. Например, помочь может достоверное априорное знание, что некто - точно рыцарь. Также не исключено, что может помочь точное знание количества рыцарей в группе.Например, если мы знаем, что все в группе - рыцари, то решение есть (тогда и спрашивать незачем). И если рыцарей n-1, то тоже вроде бы есть. А вот если только 1, то вроде бы нету?
P.S. И насчет собеседования. Там вовсе не всегда даются корректные задачи, так как собеседующего может интересовать не только способность кандидата найти верный ответ, но и ход его рассуждений

Galamaly Автор
10.12.2022 00:00Я указала на ошибку @ksbes - решать задачу, считая сколько раз кого назвали рыцарем, не имеет смысла. Так она не решится. Нужно смотреть систему - структуру кто и кого называет рыцарем. Пример: что если первый назвал второго рыцарем, а второй говорит, что первый врет? Правильно, значит первый гарантировано лжец.
«Решение выглядит слабо» - это не аргумент. Я уверена в своем решении. Повторно никого не опрашиваем, какой смысл? Все будут повторять исходную позицию. Иначе они окажутся лжецами и обнаружат себя.
Тут опять ошибка из пункта 1.

adeshere
10.12.2022 02:151. Да, согласен: невозможность решить задачу каким-то одним способом не означает, что ее нельзя решить по-другому.
2. Наверно, я не очень точно выразился, сказав, что "решение спорное". В первую очередь я имел в виду, что читателю трудно понять и оценить корректность этого доказательства (а вовсе не то, что оно ошибочное). Ведь чтобы решение было принято сообществом, оно должно быть ясным и легко проверяемым. Ход обсуждения показывает, что в нашем случае
это не так
Понимаете, для читателей Ваша уверенность в правильности решения не является аргументом. Как и уверенность Тинькофф-а. Как бы замечательно мы к вам обоим не относились, базовый принцип науки - подвергай все сомнению. Даже то, что до тебя проверено многократно и под разным углом. А вдруг предшественники не учли какое-то обстоятельство? Поэтому нельзя обвинять человека только за то, что он пытается что-то оспорить. Надо разбираться в деталях и доказывать правоту аргументами. История учит, что все прочие варианты очень опасны, так как человек, который сперва безапелляционно отвергает явную чушь, через какое-то время может сам стать авторитетом и будет так же безапелляционно "деклассировать" тех, кто пытается указать ему на совершенно реальные ошибки и баги.
3. А вот Ваше замечание по пп.3 я
не совсем понял
Возможно, дело опять в несовершенстве формулировок? Попытаюсь исправиться. В своем комментарии я для начала рассмотрел модельный случай, обобщающий обсуждаемую задачу. Часто бывает, что более общая задача решается проще, чем частный случай (ну или она хотя бы наводит на свежие мысли о возможных подходах к решению). Но оказалось, что если мы вообще ничего не знаем о жителях, то решения нет. Затем я привел примеры, показывающие, что при наличии априорной дополнительной информации решение может существовать, а может и нет. Например, при большом n (каюсь, это я тоже не уточнил - думал, что из контекста понятно) дополнительная информация, что рыцарей ровно n-1 достаточна, чтобы найти решение. А дополнительная информация, что рыцарей ровно 1 - гарантирует, что решения нет.
Обсуждаемая задача n=35+15 - это промежуточный случай между двумя этими крайностями. Соответственно, я даже не пытался ответить: разрешима она, или нет. Если какая-то из моих формулировок подтолкнула Вас к другому прочтению - буду благодарен за указание, чтобы избегать таких ошибок в дальнейшем
Я ведь не предлагал свой способ решения, и не доказывал, что он приводит к неудаче. У меня в пп.3 вообще нет выводов о разрешимости вашей конкретной задачи. Есть только два контрпримера аналогичных задач с другими значениями n, Р и Х...

adeshere
10.12.2022 00:41+2Вдогонку.
Посмотрел UPD и ответ из учебника. Действительно, рассмотрение крайних случаев (рыцарь только 1 и рыцарей n-1) навело меня на правильную идею, что точное знание количества количества рыцарей и хитрецов иногда может дать ту самую дополнительную информацию, чтобы задача стала разрешимой. Нам повезло, что задачка из статьи - это как раз такой случай. Хотя я подозреваю, что цифры в ней подобраны специально ;-)
Получается, что хотя в общем случае решения нет, но в некоторых конкретных случаях оно есть. Так что спасибо за задачку! Хотя мне, как физику, всегда приятнее находить ответ в общем случае и затем подставлять конкретные цифры в готовую формулу ;-)
P.S. Но вот решение, предложенное в статье, действительно неудачное. Де-факто нам нужно суммарно опросить m человек в произвольном порядке. Поэтому любое решение, которое разбивает процедуру опроса на этапы - переусложнено. Решение из учебника гораздо логичнее и понятнее.

Galamaly Автор
10.12.2022 11:13+1Общее решение тоже есть.
Я описала решение с островом 15-35. Но его можно экстраполировать и на другие цифры.
Самый сложный случай для поиска лжеца - это ситуация, когда опрашиваемые делятся на цветовые группы по своим показаниям. Красные - за красных. Синие - за синих. И все ссылаются еще на маленькую группку неопрошенных, которые не попали в выборку. То есть если бы задача была про 1000 островитян, где 800 лжецов и 200 рыцарей, то она бы тоже имела решение.
Мое решение (из статьи) довольно стройно и логично. Где вы увидели этапы в опросе островитян? Я рассказывала об этапах поиска решения. Когда сначала берем группы по 15 человек, а потом догадывается, что можно же было по-другому.
Решение: отобрать 47 человек. Спросить у каждого, где 15 рыцарей. Получить ответы и на их основе мы точно найдем лжецов.
Почему мы найдем ответ - об этом решение в статье. Потому что в самом умном случае лжецы разделятся на группы 11-11-11-13.
А если они поступят по-глупому и не разделятся, то вычислим сразу.
Alexandroppolus
10.12.2022 19:02+3То есть если бы задача была про 1000 островитян, где 800 лжецов и 200 рыцарей, то она бы тоже имела решение.
Нет. Тогда "лжецы" могут разбиться на 4 группы, и всего будет 5 групп по 200 чел, причем каждая группа считает только себя правдецами. И никакими вопросами не получится их различить.
В общем виде решение есть, только если количество лжецов не делится нацело на количество рыцарей.

materiatura
11.12.2022 13:32Я в своем решении тоже делил число лжецов на рыцарей, а потом смотрел на остаток.

leok
09.12.2022 19:59+2Вы выравниваете суммы отметок в "досье", но это не просто суммы. Каждый хитрец не может сказать, что он хитрец, и на этом строится решение.
то они не смогут этого сделать только, если KN > N — KN
Поэтому это неверное утверждение. Даже если суммы равны, у них есть структура.

vlad-kras
10.12.2022 10:08Каждый хитрец не может сказать, что он хитрец, и на этом строится решение.
хитрец не должен говорить, что он является хитрецом, т.к. в этом случае получаем тривиальное решение задачи
@Galamaly
Предлагаю это утверждение явно добавить в решение самым первым шагом. Шаг очевидный, но все же для большей ясности.И еще добавить в условие задачи, что
формулировка вопроса к каждому участнику имеет всегда одинаковый вид «укажи ВСЕХ негодяев»
все негодяи знают нашу цель (найти хотя бы одного из них) и хотят помешать нам
негодяи дают тот ответ, который считают нужным (формулировка «не различали истину и вымысел» очень расплывчата)
имеют возможность сговориться о своих ответах уже после отбора группы опрашиваемых (иначе придется делать неочевидные предположения, что отобранные персонажи не просто знают ответы других, но и мгновенно перестраивают свою стратегию исходя из полученных ответов)
Иначе условия задачи начинают трактовать по-разному.

Galamaly Автор
10.12.2022 10:25+1Если хитрец, скажет, что он хитрец - задача решена. Рыцари так сказать про себя не может. То есть это самый удачный случай для нас. Но нам нужно гарантированно найти 1 лжеца, а значит на такую удачу полагаться не стоит. Нужно рассматривать самый сложный вариант, чтобы гарантированно найти 1 лжеца.
Да, опрашиваемых спрашивают про всех - кто рыцарь и кто лжец.
Негодяям необязательно знать нашу цель или сговариваться или еще что-то. Они могут вести себя абсолютно случайным образом. Наша задача - отобрать столько человек, чтобы ТОЧНО вычислить 1 лжеца. Что при этом делают лжецы - вообще без разницы. Но если они ведут себя глупо - мы быстро их вычисляем. Поэтому предполагаем, что они будет вести себя умно (даже случайным образом).

leok
10.12.2022 10:51+1Это утверждение добавлять не надо. Это утверждение является первым и ключевым шагом решения и следует из условия.
Я бы нормально написал, что лжецы могут говорить и правду и ложь и вообще называл бы их хитрецами, как это принято. "Не различают истину и вымысел" - ужасный способ формулировки, откуда они тогда знают кто говорит правду вообще? Они вообще не должны быть способны понять вопрос про лжецов/рыцарей, если истину и вымысел не различают.
И к вопросу про необходимый размер выборки стоит добавить, что это необходимо сделать гарантированно. Потому что иначе я могу спорить, что ответ "1" подходит, потому что мне может повезти.

vlad-kras
10.12.2022 18:56Это утверждение добавлять не надо. Это утверждение является первым и ключевым шагом решения и следует из условия.
Если это ответ на мое сообщение про «хитрец не должен говорить, что он является хитрецом, т.к. в этом случае получаем тривиальное решение задачи», то не соглашусь.
Во-первых, в решении не обязательно это утверждение будет первым и/или ключевым. В решении Оценка сверху, 2 способ с фотографии в конце статьи это утверждение вообще отсутствует.
Во-вторых, выше https://habr.com/ru/post/704554/#comment_24994138 утверждается, что
Так как хитрец может случайно отвечать на все вопросы точно так же, как отвечал бы на его месте рыцарь. ... мы в принципе не сможем отличить его от рыцаря со стопроцентной гарантией.
Видимо, этот ключевой шаг решения не совсем очевиден.

leok
10.12.2022 20:59Может быть он не очевиден, но он определенно следует из условия.
мы в принципе не сможем отличить его от рыцаря со стопроцентной гарантией
Только нам не нужно отличить каждого лжеца, нам нужно найти одного из 35. И лжец не может отвечать так же как рыцарь потому что он говорит про себя тоже.

Kriminalist
09.12.2022 17:22+4Когда мы спрашиваем жителя, кто рыцари, а кто лжецы, он указывает на 15 потенциальных рыцарей и 35 лжецов
Рыцарь да, а лжец не обязательно. Конечно, он сразу себя выдаст таким ответом, но он же не отличает правду и вымысел, так что у него нет оснований давать ответ именно 15\35. Какова вероятность того, что лжец даст ответ именно в правильной пропорции?

Galamaly Автор
10.12.2022 11:19А нам не нужно считать вероятность.
Нужно гарантированно найти лжеца.
Поэтому даже маленькая вероятность возможна.

Festelo
09.12.2022 17:3415 человек могут назвать себя рыцарями, команда А
другие 15 человек могут назвать себя рыцарями, команда Б
Остальные 20 человек могут назвать рыцарями/лжецами всех, называя неверное кол-во человек, команда В - явно лжецы.
Невозможно понять какая из команд является командой рыцарей.
Вполне возможная ситуация.
vassabi
09.12.2022 17:46+1ну вот первый не из этих двух команд и будет вруном :)
в общем - такой себе замаскированный принцип дирихле

Festelo
09.12.2022 17:50+1Ну да, логично. Задача же состоит в том, чтобы найти хотя бы одного лжеца, а не вычислить всех. Плохой сон влияет на внимательность. Спасибо за то, что обратили мое внимание.

vassabi
09.12.2022 17:45+1а почему 47 а не 46?
там же на 45 людях в худшем случае будет три группы по 15 человек (рыцари и две группы сговорившихся врунов), а уже 46й и будет врунUPD: а не, действительно 47.
там если соберутся 4 команды, то на 46 людях им еще хватит остатка, чтобы иметь шанс сговориться, а на 47 - уже нет.

Galamaly Автор
09.12.2022 17:59Потому что худший случай - это не 15-15-15 -1 , а другой:
11 - 11 - 11 - 13
И тогда останется 4 человека, которые не попали в выборку: 2 из них все называют рыцарями, и 2 называют рыцарями первые 3 группы по 11 человек, а четвертая группа из 13 человек называет последних 2 - врунами.

vassabi
09.12.2022 18:04лжецы и рыцари - это все чтобы запутать :)
лучше считать, что там 15 простых граждан с паспортом своей страны, и 35 шпионов, у которых в кармане - какие угодно паспорта (но не паспорта простых граждан). Их задерживают, и пока везут для обыска - они могут сговориться и выбросить "лишние" паспорта по дороге, оставив себе один (как у простого гражданина).Сколько нужно задержать для обыска, чтобы поймать хотя бы одного шпиона ?
Все шпионы всегда будут называть свою группу из 15 человек "мы соотечественники", но только при 47 - у кого-то из задержанных не хватит группы, потому что в худшем случае для простых граждан - их будет 12 (3 не задержаны), а у остальных на 12 не наберется (ибо 12*4 = 48)

ShashkovS
09.12.2022 19:37+4Ох... ИМХО, называть хитрецов (по классике) лжецами (которые в 100% классики всегда только лгут) примерно как обозначать тангенс через tanh. Можно написать длинючий красивый абзац о том, что tanh в этой задаче — это отношение синуса и косинуса, но все те, кто привык к обозначению tanh — гиперболический тангенс — вас будут про себя материть (и решать не ту задачу).
И это не будет зависеть от того, кто сформулировал так задачу, Тинькофф, Сбер или сам Перельман.Но задача прикольная, именно такой формулировки ещё не встречал.
Если по сути, то решение из учебника мне кажется куда более понятным.
Ясно, что в статье ход ваших мыслей, но уж очень затянуто для решения логической задачи.

leok
09.12.2022 20:05+6Очень странно видеть многократные упоминания Тинькофф как высшего авторитета математики. Лично у меня вызывает прямо противоположный эффект.

Galamaly Автор
09.12.2022 22:28-2У них отличные математические олимпиады. Рекомендую.
На авторитет ссылаюсь, потому что в глупости своей комментаторы не ведают что творят. И обижают. Приходится защищаться.

BMXer_V
10.12.2022 00:36+5Долго терпел, но после этого комментария влепил вам минус в карму. Не надо считать, что только вы и абстрактный Тинькофф умные, а все остальные - глупцы.

Galamaly Автор
10.12.2022 10:49-3Жаль, что вашего выстраданного терпения не хватило на то, чтобы разобраться с решением задачи, и понять, что комментарии формата "условия двояки и туманны" только путают всех остальных, тк условия максимально четкие, а уступки формата "сговрились", "видели ответы друг друга" и тд - не имеют смысла (тк без разницы, как ведут себя лжецы, нам нужно гарантированно при любом их поведении найти ответ).
Жаль, что вы так уверены в своих силах и мозгах.
Жаль, что так много людей не готовы изучить вопрос и внимательно прочитать условия.
Горжусь минусом от вас. Продолжайте!
BMXer_V
10.12.2022 12:38+3Я как раз-таки не уверен в своих мозгах. Поэтому никогда не буду называть всех подряд "глупцами".
Я и ещё несколько человек написали вам, что если в дискуссии, особенно в математической, вы регулярно оскорбляете оппонентов и ссылаетесь на авторитет, вместо того чтобы аргументированно ответить, то ничего хорошего из этого не выйдет. Но вы, похоже, так ничего и не поняли, хотя и считаете себя самой умной здесь...

Galamaly Автор
10.12.2022 15:11-3Давайте по существу задачи. А без этой демагогии, кто кого кем считает, и кто тварь дрожащая, а кто право имеет.

adeshere
10.12.2022 01:05+3Приходится защищаться.
Простите за бестактность, но мне кажется, что Вы выбрали
не очень удачный формат защиты
Статьей Вы инициировали дискуссию, а это вроде как подразумевает моральное обязательство продолжить содержательный разговор в комментариях. Когда человек выкладывает свой вариант решения, то он ожидает, что ему либо укажут на ошибку в решении, либо пояснят, что он неточно понял формулировку задачи (причем тут может быть вина обеих сторон), либо согласятся с его вариантом. Если же вместо этого следует отсылка к авторитету, то, образно говоря, это напоминает удар кулаком по столу, что, естественно, очень плохо воспринимается в математическом споре.

Galamaly Автор
10.12.2022 07:46+2Во-первых, благодаря тому, что комментаторы не разбираются, а просто ставят минус мне в карму, минус в статью и минус в мой комментарий, я не могу комментировать свою же статью (меня просто банят и я могу оставлять 1 комментарий в 1 час). Теперь понимаете, почему я злюсь?
Во-вторых, я объясняю, привожу аргументы. Их снова минусуют. Давайте соберу в этом комментарии все мои попытки объяснить то, что не поняли комментаторы. Жду ваши минусы)
Людей опрашивают, кто лжец, а кто нет - то есть каждого из выборки спрашивают относительно всех 50 островитян. Если житель назовет себя лжецом - он лжец. Тк рыцарь так сделать не может, он всегда говорит правду. Если житель назовет 20 рыцарей, он лжец, тк рыцарей всего 15. То есть если житель сглупит, задача решится легко. Но нам нужен самый сложный случай. Тк нужно гарантировано найти хотя бы 1 лжеца.
Сговариваются ли жители? Без разницы. В объяснении я пишу «сговариваются», чтобы продемонстрировать, что у них одинаковые ответы. Могут ли они получиться рандомным путём? Конечно. Не важно, какая вероятность такого исхода, достаточно того, что она есть. И это будет тот самый сложный случай, когда сложно определить лжеца. Стоят перед вами 11 зелёных, 11 красных, 11 синих и 13 желтых и называют рыцарями каждый свою группу. Кому поверить? А в сторонке еще 4 человека, 2 из которых все называют рыцарями, а 2 других - рыцари у первых 3 цветных групп.
Почему неправильно просто считать отметки «рыцарь», «лжец» - потому что это не приведет к ответу и вы сделаете ложный вывод, что задача не решается. Нужно смотреть структуру ответов. Если первый говорит, что второй - рыцарь. А второй, что первый - лжет. Значит первый - точно лжет. Если бы он был рыцарем, то и 2 был бы рыцарем и говорил только правду, и второй бы тогда сказал, что и первый рыцарь. Но этого не произошло, а значит первый - точно лжец (2 тоже может быть лжецом, но это не важно, тк одного нужного лжеца мы найдем и задача будет решена).
Сколько раз опрашивают жителей? По одному. Какой смысл повторять им вопрос? Если ты рыцарь, то будешь придерживаться 1 точки зрения. Если лжец - то можешь ее поменять, но таким образом сразу выдашь себя. Но нам нужно гарантировано найти хотя бы 1 лжеца, а значит такие простые ситуации, когда кто-то себя сам выдает мы не рассматриваем. Такая ситуация была бы удачей при решении. Но мы берём самый трудный случай, чтобы точно найти лжеца.
Может ли лжец говорить только ложь или может говорить и то, и то? В моей картине мира, лжец, который всегда врет, - это «идеальный» лжец. Если задавать ему вопрос с 2 вариантами ответа, то мы всегда узнаем правду (зная что он 100% лжец). Куда логичнее, чтобы лжец то врал, то нет. Назовём его «хитрец». Обращение к терминам тангенса в комментариях не корректно, тк tg - это общепринятое сокращение. Лжец, хитрец и тд - это всего лишь мысленный эксперимент из теории игр. Нет никакого принятого определения, что есть лжец. Просто тот, кто врет. Всегда ли он врет? Про это есть объяснение в условиях моей задачи.
Теперь про Тинькофф. Не знаю, за что вы против них ополчились. У них классные Олимпиады по математике, очень крутые отборы на позиции в аналитику и DS. Много интересных задач. Я ссылалась на них, чтобы меня перестали воспринимать дилетантом от мира математики. Мол - «эй, хватит минусить, прочитайте ВНИМАТЕЛЬНО решение в статье. Там же все расписано. Просто - внимательнее. И подумайте, порисуйте. Зачем сразу критиковать и писать «лень искать ошибку, но вы не правы»?
И, наконец, про решение в общем случае. Кто-то пишет, что его нет. Есть конечно. Я ведь показала метод решения. Самый сложный случай для поиска лжеца - это ситуация, когда опрашиваемые делятся на цветовые группы по своим показаниям. Красные - за красных. Синие - за синих. И все ссылаются еще на маленькую группку неопрошенный, которые не попали в выборку. То есть если бы задача была про 1000 островитян, где 800 лжецов и 200 рыцарей, то она бы тоже имела решение.

StjarnornasFred
10.12.2022 23:58+1Может ли лжец говорить только ложь или может говорить и то, и то? В моей картине мира, лжец, который всегда врет, - это «идеальный» лжец. Если задавать ему вопрос с 2 вариантами ответа, то мы всегда узнаем правду (зная что он 100% лжец). Куда логичнее, чтобы лжец то врал, то нет.
Извините, но мы обсуждаем не картину мира, а класс логических задач. Задачи про рыцарей и лжецов по определению предусматривают, что рыцари всегда говорят правду, а лжецы всегда лгут. Это задачи на математику и логику, а не на философию, право или мораль. И ответ "Я - лжец" в таких задачах в принципе невозможен, гуглить парадокс лжеца.

zlat_zlat
10.12.2022 05:21+2Оставил вашу статью вчера в закладках, но сегодня понял, что дело дрянь.
Вы уж извините, но с подобной «защитой» вам долго не протянуть в сообществе. Люди не любят, когда им говорят, что они глупцы, просто потому, что их мнение не совпадает с вашим авторитетом. Обижают? Ну, знаете ли, мы же не в средней школе, и едва ли тут можно предположить намеренный буллинг. Скорее, это реакция на ваши методы вести дискуссию.

Galamaly Автор
10.12.2022 10:58-1Дело - дрянь, согласна. Говорить глупцам, что они сглупили - бессмысленно. Хоть с 1000 аргументов. Куда проще поставить минус автору и уйти пить чай с мыслью о своем величии.

aamonster
11.12.2022 01:23+2Сочувствую.
Я пока не решил задачку (в ваше решение специально не вникал, приятнее разобраться самому), но отчётливо вижу, за что вас минусуют. Высокомерие крайне скверно влияет на репутацию...

leok
10.12.2022 10:36+2Есть много людей которые круто разбираются в математике, но ссылаться на них как авторитет в случайной аудитории бесмысленно. Даже если люди из околоматематических дисциплин.
в глупости своей комментаторы не ведают что творят
Это в купе с отсылками к Т выглядит как будто вы просто самоутверждаетесь. "Вы что, не знаете Тинькофф?! Пфф"

Areek
09.12.2022 20:35Вообще, по условию задачи:
Рыцари были настолько горды и благородны, что не могли говорить ничего, кроме правды, правды и только правды. А лжецы не различали истину и вымысел.
Достаточно собрать 16 человек и, отводя по одному, задать каждому вопрос "кто из вас 16ых всегда говорит правду/лжец". Рыцари покажут честными ТОЛЬКО друг на друга или на себя одного (Команда рыцарской поруки), а лжец(ы) - на всех или на кого попало. Для лжеца по условию задачи нет различий, они все - правдивы. Но он ведь не обязательно так скажет, потому что лжец)))
Идея в том, что лжецы, будь их 1, 15 или 16, не смогут организовать команду рыцарской поруки, как это сделают рыцари, будь их 2-15, а одинокий рыцарь с фразой "тут честен только я" будет заметен в группе тычущих друг в друга лгунов.Если же имеет место сговор, то это другая задача и решаться она должна иначе.

twid
09.12.2022 21:24А мне все нравится. Т.е. рыцарь - называет рыцаря рыцарем, лжеца лжецом. В том числе себя, что важно. Лжец называет кого угодно как угодно, в том числе себя. Лжецы могут договориться как угодно с целью, чтобы проскочил систему хотя бы один из них.
Сколько ни выберем человек, спросить можно один раз.
При отборе 31 человек как ни спроси, лжеца найдешь. Последовательно ли, про всех ли, "покажи пять лжецов" - гарантировано одного выцепишь. А вот меньше - надо думать.

Andreyul
09.12.2022 22:32-1Моё решение.
Выберем группу (A) из N человек. Их опросим. В оставшейся группе (B), 50-N человек.
Для каждого N, начиная с N=1, находим наихудший (неудачный) случай. Если в таком случае лжеца найти нельзя, увеличиваем N на 1 и повторяем.Для любого N=[1;35]:
Пусть все N в группе A - лжецы. Каждый говорит: "Я рыцарь. Другие в группе A - лжецы." Найти лжеца нельзя.Для N=36.
Пусть 1 в группе A - рыцарь, 35 - лжецы. Каждый говорит: "Я рыцарь. Другие в A - лжецы." Найти лжеца нельзя.
Для N=37.
Пусть 2 в группе A - рыцари, 35 - лжецы. 2 рыцаря говорят: "Мы 2 рыцаря. Другие в группе A - лжецы". 35 лжецов делятся на 3 подгруппы A1=11, A2=11, A3=13. Каждая подгруппа говорит: "Мы, подгруппа Ax, - рыцари. Другие в A - лжецы". Найти подгруппу лжецов нельзя.
...
Для N=46.
Пусть 11 в группе A - рыцари, 35 - лжецы. 11 рыцарей говорят: "Мы 11 рыцарей. Другие в A - лжецы". 35 лжецов делятся на 3 подгруппы A1=11, A2=11, A3=13. Каждая подгруппа говорит: "Мы, подгруппа Ax, - рыцари. Другие в A - лжецы". Найти подгруппу лжецов нельзя.Для N=[36;46] в вышеописанных худших случаях рыцари из группы A говорят, что вся группа B - рыцари. Лжецы из группы A говорят то же самое.
Для N=47.
Пусть 12 в группе A - рыцари, 35 - лжецы. 12 рыцарей говорят: "Мы 12 рыцарей. Другие в A - лжецы". 35 лжецов не смогут разделиться на подгруппы, чтобы в каждой подгруппе было >=12 и <=15 человек. Подгруппа, в которой <12 или >15, - лжецы.
Пусть 13 в группе A - рыцари, 34 - лжецы. 13 рыцарей говорят: "Мы 13 рыцарей. Другие в A - лжецы". 34 не делится на подгруппы [13;15]
Пусть 14 в группе A - рыцари, 33 - лжецы. 14 рыцарей говорят: "Мы 14 рыцарей. Другие в A - лжецы". 33 не делится на подгруппы [14;15]
Пусть 15 в группе A - рыцари, 32 - лжецы. 15 рыцарей говорят: "Мы 15 рыцарей. Другие в A - лжецы". 32 не делится на подгруппы по 15.
Все 4 возможных варианта позволяют гарантированно вычислить подгруппу лжецов.Ответ: 47.

materiatura
10.12.2022 11:39+1Я - тугодум, я больше часа думал. Формулировка хоть и не идеальная, но претензии к ней еще менее точны. В формулировке не хватает указания, что мы знаем количество рыцарей и лжецов. Если не знаем, то задача не решаемая.
По лжецам, которые хитрят. Если лжецы будут лгать на каждый вопрос из 50-ти, то задача уж очень проста - нам достаточно опросить 16 человек.
Задача решена верно, для определения хотя бы одного лжеца нужно 47 допросов, но при этом мы определим в лучшем случае 33 лжеца и 14 рыцарей, а не всех, в худшем 11 лжецов и не определим ни одного рыцаря. Но решение, на мой взгляд, не очень изящное, да простит меня автор. Хотя это дело вкуса. Решение в учебнике повеселее, но тоже оставляет желать лучшего.
Из любопытного: При правильной тактике лжецов мы сможем определить только 5 из них, и не сможем определить ни одного рыцаря. Это скорее к теории игр примечание.

amakhrov
11.12.2022 08:19Задача интересная, спасибо. В приведенном ходе решения, по-моему, пропущены какие-то шаги. Например, почему худший случай - это 4 "команды", а не 5? Или в случае 4 команд есть вариант 11-11-12-12, а не 11-11-11-13 (что, конечно, даст все тот же ответ 47 - но все же)


Galamaly Автор
Во-первых, благодаря тому, что комментаторы не разбираются, а просто ставят минус мне в карму, минус в статью и минус в мой комментарий, я не могу комментировать свою же статью (меня просто банят и я могу оставлять 1 комментарий в 1 час). Теперь понимаете, почему я злюсь?
Во-вторых, я объясняю, привожу аргументы. Их снова минусуют. Давайте соберу в этом комментарии все мои попытки объяснить то, что не поняли комментаторы. Жду ваши минусы)
Людей опрашивают, кто лжец, а кто нет - то есть каждого из выборки спрашивают относительно всех 50 островитян. Если житель назовет себя лжецом - он лжец. Тк рыцарь так сделать не может, он всегда говорит правду. Если житель назовет 20 рыцарей, он лжец, тк рыцарей всего 15. То есть если житель сглупит, задача решится легко. Но нам нужен самый сложный случай. Тк нужно гарантировано найти хотя бы 1 лжеца.
Сговариваются ли жители? Без разницы. В объяснении я пишу «сговариваются», чтобы продемонстрировать, что у них одинаковые ответы. Могут ли они получиться рандомным путём? Конечно. Не важно, какая вероятность такого исхода, достаточно того, что она есть. И это будет тот самый сложный случай, когда сложно определить лжеца. Стоят перед вами 11 зелёных, 11 красных, 11 синих и 13 желтых и называют рыцарями каждый свою группу. Кому поверить? А в сторонке еще 4 человека, 2 из которых все называют рыцарями, а 2 других - рыцари у первых 3 цветных групп.
Почему неправильно просто считать отметки «рыцарь», «лжец» - потому что это не приведет к ответу и вы сделаете ложный вывод, что задача не решается. Нужно смотреть структуру ответов. Если первый говорит, что второй - рыцарь. А второй, что первый - лжет. Значит первый - точно лжет. Если бы он был рыцарем, то и 2 был бы рыцарем и говорил только правду, и второй бы тогда сказал, что и первый рыцарь. Но этого не произошло, а значит первый - точно лжец (2 тоже может быть лжецом, но это не важно, тк одного нужного лжеца мы найдем и задача будет решена).
Сколько раз опрашивают жителей? По одному. Какой смысл повторять им вопрос? Если ты рыцарь, то будешь придерживаться 1 точки зрения. Если лжец - то можешь ее поменять, но таким образом сразу выдашь себя. Но нам нужно гарантировано найти хотя бы 1 лжеца, а значит такие простые ситуации, когда кто-то себя сам выдает мы не рассматриваем. Такая ситуация была бы удачей при решении. Но мы берём самый трудный случай, чтобы точно найти лжеца.
Может ли лжец говорить только ложь или может говорить и то, и то? В моей картине мира, лжец, который всегда врет, - это «идеальный» лжец. Если задавать ему вопрос с 2 вариантами ответа, то мы всегда узнаем правду (зная что он 100% лжец). Куда логичнее, чтобы лжец то врал, то нет. Назовём его «хитрец». Обращение к терминам тангенса в комментариях не корректно, тк tg - это общепринятое сокращение. Лжец, хитрец и тд - это всего лишь мысленный эксперимент из теории игр. Нет никакого принятого определения, что есть лжец. Просто тот, кто врет. Всегда ли он врет? Про это есть объяснение в условиях моей задачи.
Теперь про Тинькофф. Не знаю, за что вы против них ополчились. У них классные Олимпиады по математике, очень крутые отборы на позиции в аналитику и DS. Много интересных задач. Я ссылалась на них, чтобы меня перестали воспринимать дилетантом от мира математики. Мол - «эй, хватит минусить, прочитайте ВНИМАТЕЛЬНО решение в статье. Там же все расписано. Просто - внимательнее. И подумайте, порисуйте. Зачем сразу критиковать и писать «лень искать ошибку, но вы не правы»?
И, наконец, про решение в общем случае. Кто-то пишет, что его нет. Есть конечно. Я ведь показала метод решения. Самый сложный случай для поиска лжеца - это ситуация, когда опрашиваемые делятся на цветовые группы по своим показаниям. Красные - за красных. Синие - за синих. И все ссылаются еще на маленькую группку неопрошенный, которые не попали в выборку. То есть если бы задача была про 1000 островитян, где 800 лжецов и 200 рыцарей, то она бы тоже имела решение.