06.11.2022 17:44
Galamaly 61 15000 Источник

В общем случае задача выглядит как поиск знаков арифметических операций и иных действий без использования других цифр для того, чтобы получить из четырёх двоек любое число от 0 до 9.

Довольно простые решения на сложение, деление и возведение в степень есть для всех чисел, кроме 7.

С 7 же нужно выйти за рамки привычного (помните головоломку про соединение точек и выход из зоны квадрата). По решению задачи можно многое узнать о собеседнике.

На этом моменте предлагаю остановиться тем, кто хочет испытать свои силы.

You shall not pass
You shall not pass

Первое решение - это читерское округление. Корень из 222, делённый на 2, это иррациональное число 7.44983..

Решение грубое, но действенное.

Следующий путь - использование логарифма. В какую степень надо возвести 2, чтобы получить корень из 2. А если взять из результата логарифм по основанию 2?

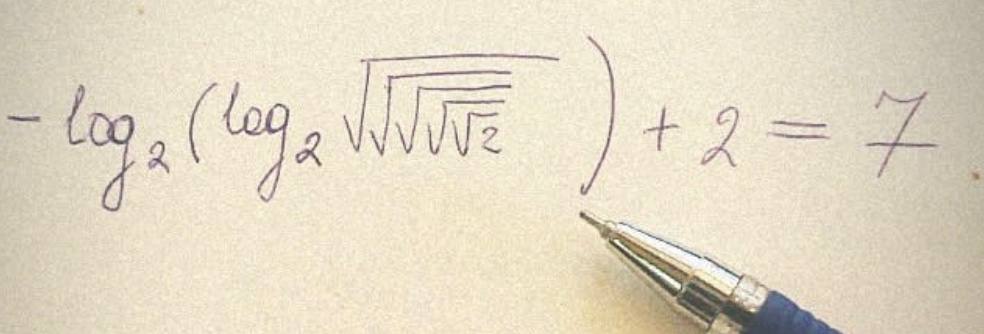
Для тех, кто помнит логарифмы и никогда не боялся двойного интеграла
Для тех, кто помнит логарифмы и никогда не боялся двойного интеграла

Это решение для сильных духом, которые всегда найдут ответ. Ведь у любой операции (возведение в степень) есть обратная.

Третий вариант - двойной факториал. Двойной факториал (перемножение с шагом 2) от 4 это 4*2=8.

2*2!! - 2/2 = 7

Факториал не изучают в школе, но он точно нужен в комбинаторике и мат анализе, поэтому такое решение подвластно тем, кто не забыл свои первые курсы в универе, хотя тогда казалось, что высшая математика в жизни не пригодится.

Четвёртое решение - элегантная перестановка слагаемых.

2/2 = 7 в степени (2-2)

Тоже читерство, но уже другого рода. Если что-то мешается, то можно это вынести за знак равенства и сделать с этим что-то уже там. Я бы сказала, предпринимательский подход. Решение предложил один из бывших руководителей Газпрома.

Пятое решение - это тригонометрия. Подход визуализаторов.

cos(2pi) + 2 + 2 + 2 = 7

sin(pi/2) + 2 + 2 + 2 = 7

Легендарное Пи - это, конечно, не цифра. Но ее использование открывает дверь к решениям с константой.

6) 2 + 2 + 2 + 2 - x/x = 7

И, наконец, седьмое решение. Мое любимое. Очень прогерское.

222/2 = 111

А 111 в двоичной системе исчисления - это искомое семь.

Пока это все решения, которые удалось найти. Если у вас есть что-то ещё, пишите в комментариях.

Комментарии (61)


  1. zloddey
    06.11.2022 17:53
    #24887340
    +39

    Python:

    >>> (2 << 2) - 2/2
7.0

    Битовый сдвиг на 2 позиции - аналог умножения на 4.


  1. mobi
    06.11.2022 18:02
    #24887366
    +18

    (F2+2)2−2=7, где Fn — числа Фибоначчи (F4=3).


    1. Galamaly Автор
      06.11.2022 20:20
      #24887700
      +1

      Сначала хотела написать, что последовательность включает две единицы, а значит четвертый член - это 2. А потом вспомнила, что счёт начинаем с 0.
      Беру решение в копилку)


    1. mobi
      06.11.2022 20:20
      #24887702
      +3

      Еще вариант: ⌊2+2+2+√2⌋ (тут ⌊x⌋ — взятие целой части числа).


      1. Galamaly Автор
        06.11.2022 20:25
        #24887732
        -2

        Это уже на так красиво. С округлением есть решения проще


  1. Vindicar
    06.11.2022 18:32
    #24887418

    del


  1. 411
    06.11.2022 18:47
    #24887444
    +4

    p_{2+2+2-2}


  1. iShrimp
    06.11.2022 19:05
    #24887502
    +8

    Ещё один прогерский вариант:

    2 / (2 * .2) + 2


    1. lain8dono
      06.11.2022 23:59
      #24888280
      +2

      Недостаточно прогерский вариант. Вот лучше:

      2 + 2 + 2 + count_trailing_zeros(2)


  1. Arastas
    06.11.2022 19:45
    #24887614
    +5

    2*2*2-sign(2)=7


  1. sunnybear
    06.11.2022 20:06
    #24887660
    +30

    2+2+2-i^2
    Через мнимую единицу


    1. maximw
      06.11.2022 20:12
      #24887686
      +1

      Вот это изящнее всех вариантов, на мой взгляд.


      1. Galamaly Автор
        06.11.2022 20:23
        #24887722
        +1

        выход из зоны рациональности) красиво


        1. maximw
          06.11.2022 20:49
          #24887806
          +7

          Пусть не рациональное, зато комплексное решение.


      1. sunnybear
        06.11.2022 21:31
        #24887908
        +1

        Спасибо, но мне с Фибоначчи больше понравилось :)


    1. RusikR2D2
      07.11.2022 08:46
      #24888788
      +4

      Но i - это все же своеобразная "цифра" (число), что выходит за условия задачи. Иначе можно использовать шестнадцатиричные "буквы". Где В-А =1. 2+2+2+2-(В-А)=7


      1. Alexandroppolus
        08.11.2022 15:01
        #24893520

        Но i - это все же своеобразная "цифра" (число), что выходит за условия задачи

        Именно. Нельзя юзать константы.

        С комплексными числами ниже есть очень крутое решение (где arccos(2))


  1. murkin-kot
    06.11.2022 21:01
    #24887844
    +2

    2*2!! - log2 2

    Здесь log2 - логарифм по основанию 2.


  1. andreishe
    06.11.2022 21:40
    #24887940
    +5

    Если уж читерить, то исправляйте «равно» на «не равно».


  1. PastorGL
    06.11.2022 21:57
    #24888000
    +1

    Постойте, факториал теперь и вправду не изучают в школе?


    Ужас какой. Я закончил в 1997, у нас была комбинаторика.


    1. Koioes
      07.11.2022 05:58
      #24888608
      +1

      Изучают, конечно. На комбинаторику целых 3 задачи в ЕГЭ.


      1. Galamaly Автор
        07.11.2022 05:59
        #24888610

        Я закончила в 2005, мы довольно глубоко уходили в интегралы, а вот комбинаторику не помню. Но вы, очевидно, правы


    1. fransua
      07.11.2022 10:27
      #24889054

      Тут какой-то Двойной факториал


  1. EskakDolar
    06.11.2022 22:08
    #24888042

    Видел много разных надписей на партах в вузе, но одна запомнилась -

    "Каждому лектору в #опу по вектору и разложить по базису..."


    1. w0lf
      06.11.2022 22:17
      #24888068
      +1

      Мне из родного ВУЗа больше всего запомнилось "Сколько поле не квантуй всё равно получишь ...й"


      1. markowww
        07.11.2022 14:39
        #24889992

        "Маньяком можешь ты не быть, но сексуальным быть обязан"


  1. nick758
    07.11.2022 04:42
    #24888566

    √((.2.../2)^-2)-2
    .2… — 0.2… (так можно записывать периодическую дробь?) соответствует 2/9


  1. TvvT
    07.11.2022 05:56
    #24888602
    +9

    А если так 22-2/2, но в троичной системе исчисления?


    1. Galamaly Автор
      07.11.2022 05:57
      #24888606

      Тоже можно) засчитано!


      1. TvvT
        07.11.2022 23:22
        #24891566

        ну и в восьмеричной 22/2-2 туда же :)


      1. AcidCyanide
        09.11.2022 15:34
        #24897332

        С использованием систем счисления можно получить семёрки до семеричной системы включительно:

        4) 22/2+2=13

        5) (22+2)/2=12

        6)22/√(2+2)=11

        7) (22-2)/2=10

        Все они при переводе в десятичную дадут 7


  1. Jorell
    07.11.2022 08:53
    #24888804

    ещё один читерский вариант:

    2*2/2/2=1 (поворачиваем изначальную 7 на несколько градусов против часовой стрелки)


  1. RusikR2D2
    07.11.2022 08:55
    #24888812
    +1

    Ещё есть "треугольные числа", не знаю насколько это официальное явление. Похоже на факториал, но сложение вместо вычитания. Т2=2+1=3, Т3=3+2+1=6 и т.д.

    Тогда решение задачи:

    2^(Т2)-2/2=7

    Ну и вариант с шестнадцатиричные и буквами, если их не считать за цифры из условия (раз уж мнимая единица не число)

    2+2+2+2-(В-А)=7


    1. Galamaly Автор
      07.11.2022 08:58
      #24888820

      Треугольные числа - это элегантно!


  1. Alexandroppolus
    07.11.2022 09:05
    #24888834
    +9

    2 + 2 + 2 + sh(arch(sqrt(2)))

    Вариант с логарифмами и корнями универсален - может тремя двойками нарисовать любое целое. Это известная задачка за авторством Поля Дирака.

    С помощью гиперболических функций можно и из одной двойки (из одного любого целого) получить любое другое целое, не привлекая какие-либо иные константы, с помощью функций U(x) = ch(arsh(x)), и D(x) = sh(arch(x)). Первая увеличивает значение под корнем (U(x) = sqrt(x^2 + 1)), вторая понижает. Соответственно, выстраиваем цепочку U(U(...U(2)...)), сколько требуется. Есть похожие формулы и для обычных тригонометрических функций.


    1. Refridgerator
      08.11.2022 08:46
      #24892228
      +1

      Здесь можно и обычной тригонометрией обойтись:
      Cos(2*ArcCos(2))*2/2


      1. Arastas
        08.11.2022 09:18
        #24892302

        Arccos(2)?


        1. Refridgerator
          08.11.2022 09:29
          #24892340

          Быстрый тест на то, знает ли человек комплексные числа дальше формальных определений. Без комплексных чисел справедливость равенства можно доказать через разложение в степенной ряд.


      1. Alexandroppolus
        08.11.2022 11:14
        #24892694

        С "обычной", как ранее говорил, тоже есть формулы для увеличения и уменьшения числа под корнем:

        U(x) = sec(atg(x)) = sqrt(x^2 + 1)

        D(x) = tg(asec(x)) = sqrt(x^2 - 1)

        Ответ можно представить, например, так:

        7 = 2 + 2 + 2 + tg(asec(sqrt(2)))

        7 = sec(atg(sqrt(2 + 2 + 2))) ^ 2

        Из одной двойки получить 7 можно так: 7 = U(U(...U(2)...)), где U(x) применяется 45 раз


        1. Refridgerator
          08.11.2022 15:14
          #24893568
          +1

          45 как-то маловато. Давайте лучше 4 937 235 раз D(x) от 2222. Или 4 294 967 247 раз от 2222.


  1. Germanjon
    07.11.2022 09:25
    #24888888
    +2

    Из трёх двоек легко получить шестёрку (2+2+2) или восьмёрку (2*2*2).
    Соответственно, можно переформулировать и вывести новую подзадачу "как математическими действиями из двойки получить единицу".


  1. LuggerFormas
    07.11.2022 12:29
    #24889566

    >> 222/2 = 111

    "Я видел двойку, я видел двойку!" - Бендер Родригез

    Не бойся, Бендер, двоек не бывает...


  1. 25352
    07.11.2022 13:02
    #24889696
    +1

    Факториал не изучают в школе, но он точно нужен в комбинаторике и мат анализе, поэтому такое решение подвластно тем, кто не забыл свои первые курсы в универе
    факториал ладно, он достаточно известен. Но вот «двойной факториал» — иной разговор. Вещь более специфичная


    1. Galamaly Автор
      07.11.2022 13:03
      #24889702
      +1

      Зато полезная, как выяснилось


  1. AviPaperno
    07.11.2022 13:29
    #24889784
    +1

    Если есть функция округление вверх, то можно так:

    ОКРВВЕРХ(2,2*2)+2 = ОКРВВЕРХ(4,4) + 2 = 5 + 2 = 7

    from math import ceil

print(ceil(2.2 * 2) + 2) ## 7


  1. 1nsan31nsId3
    07.11.2022 14:48
    #24890018
    +6

    \sqrt{\sqrt{2\%^{-2}}-2/2}


    1. Galamaly Автор
      07.11.2022 14:49
      #24890020

      Тут пусто


    1. Galamaly Автор
      07.11.2022 15:09
      #24890090

      Теперь отражается, очень изобретательно! Браво!


    1. 1nsan31nsId3
      08.11.2022 14:30
      #24893424

      Не красиво и слишком мудрено, но уж очень хотелось найти еще решение не похожее на другие. (|\overrightarrow{(2,\theta(2))}|)^2+2, где \theta(x) = [x \ge 0]- функция Хевисайда, где []- скобка Айверсона.


  1. push_banker
    07.11.2022 21:03
    #24891208
    +3

    А можно корень бесконечно раз брать? Тогда получается:

    2+2+2+√√...√√2 = 7


    1. 1nsan31nsId3
      08.11.2022 15:55
      #24893676

      Я думаю, что 1 нельзя получить бесконечно поднося 2 к степени 0.5. Или я ошибаюсь?


  1. playermet
    07.11.2022 21:28
    #24891280

    А(2,2) * 2/2
    Где A - функция Аккермана. Собственно, она сразу дает семерку при двойках в аргументах.


  1. IVgorod
    07.11.2022 23:38
    #24891594

    22/2-2=7. Система счисления восьмеричная.


  1. Igorbur
    07.11.2022 23:38
    #24891598

    Округление(22 / округление(2 * корень(2)))


  1. IkaR49
    08.11.2022 10:40
    #24892578

    Торжественно клянусь сначала читать весь текст, потом писать.


    1. IkaR49
      08.11.2022 10:42
      #24892588

      Торжественно клянусь сначала читать весь текст, потом писать.


  1. GGribkov
    08.11.2022 10:44
    #24892594

    2+2+2+(2^0)=7.

    Это так просто... Я удивлен, что этого ещё не предложили)


    1. IkaR49
      08.11.2022 10:47
      #24892604
      +1

      Ноля нет среди доступных цифр ;)


      1. GGribkov
        08.11.2022 19:00
        #24894310

        Оу. Вы правы, что-то я сглупил)


  1. evilded
    09.11.2022 15:31
    #24897320
    +2

    К чертям математику. Зачем вообще что-то менять в этом выражении, давайте просто считать символы)


  1. valerymedved
    09.11.2022 15:59
    #24897456

    2+2+2+2^0