В одном своём гисте Андрей Карпаты сделал кое-что впечатляющее. Чуть больше чем в 100 строках кода на Python — без тяжеловесных фреймворков для машинного обучения — он прописал довольно полную реализацию языковой модели для обучения символьно-ориентированных рекуррентных нейросетей (РНС). Гист включает полное обучение методом обратного распространения с оптимизацией Adagrad. Подробности — к старту флагманского курса по Data Science.

Мне нравятся такие минималистичные примеры, так как они позволяют глубже понять определённую тему, увязать математику с кодом и получить полное представление о том, как всё это работает. Я хочу дополнить объяснения к гисту Андрея Карпаты, показать диаграммы и расчёты, на которых построена работа его кода на Python.

Я форкнул этот код и создал семантический эквивалент гиста Андрея, но добавил больше комментов и некоторые опции для отладки. Не стал воспроизводить здесь всю программу. Идея не в этом, а в том, чтобы вы читали статью, заглядывая в код. Диаграммы, формулы и объяснения этой статьи дополняют комментарии в коде.

Что делают РНС?

Думаю, читатели представляют себе, как работают РНС, и понимают, почему они так хорошо справляются с некоторыми задачами. В частности, они хорошо подходят в предметных областях, где входом (и/или выходом) является некая последовательность — временной ряд с финансовыми данными, слова или предложения на естественном языке, речь и др.

Об этом в сети есть очень много материалов, основы которых хорошо поймут все, у кого есть базовые знания о машинном обучении. И всё же в сети довольно мало последовательно изложенных материалов, которые показали бы, как реализовать и обучить РНС, — в этом и заключается цель моей статьи.

Языковая модель для обучения символьно-ориентированных РНС

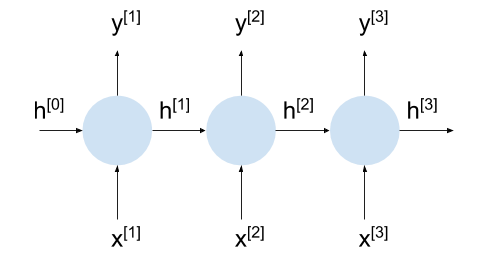
Основную структуру min-char-rnn отражает эта циклическая диаграмма, где x — входной вектор во временном интервале t, y — выходной вектор (output vector), а h — вектор состояний внутри модели.

Линия, которая выходит из ячейки и возвращается в неё, указывает, что состояние сохраняется между обращениями к сети. С наступлением новой итерации одни параметры остаются прежними (как мы скоро увидим, это весовые коэффициенты сети), а другие меняются: изменяться может h. Именно поэтому, в отличие от нестационарных сетей, y не является простой функцией x; в РНС одинаковые x могут давать разные y в силу того, что y — функция x и h, а h может меняться между итерациями.

Слово «символьно-ориентированная» (character-based) в названии модели подразумевает, что каждый входной вектор соответствует одному символу (а не слову или фрагменту изображения). В min-char-rnn для представления различных символов используются векторы с одним активным состоянием (one-hot vectors).

Языковая модель — это особый вид алгоритма машинного обучения, изучающий статистическую структуру языка путём «чтения» большого корпуса текстов. Такая модель может затем воспроизводить аутентичные языковые сегменты, предсказывая следующий символ или слово, если модель строится на основе слов, по предыдущим символам.

Внутренняя структура ячейки РНС

Перейдём к внутренней структуре ячейки РНС в min-char-rnn:

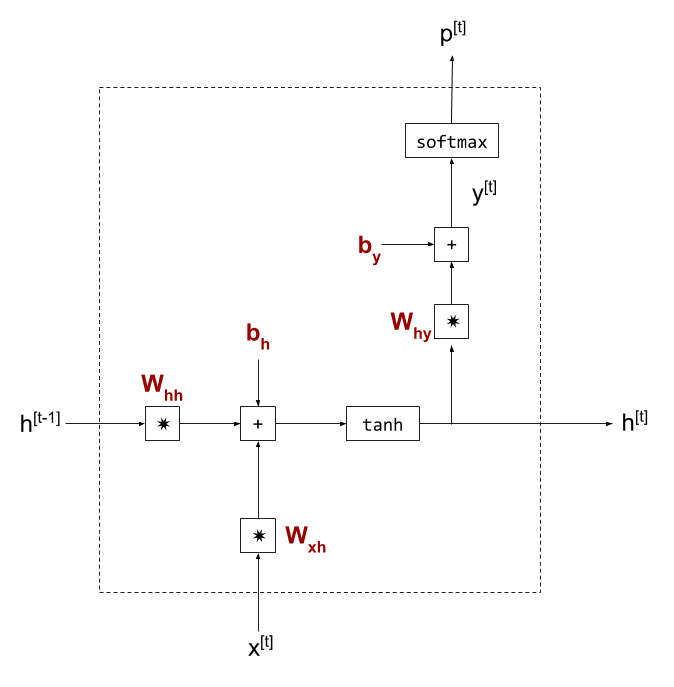
• Написанные жирным шрифтом символы бордового цвета — это параметры модели, весовые коэффициенты для умножения матрицы, а также смещения.
• Вектор состояния h показан дважды: первый — в своём прошлом значении, второй — в рассчитанном текущем значении. Каждый раз, когда последовательно вызывается ячейка РНС, слева передаётся последнее вычисленное состояние h.
• Значение y на этой диаграмме не является конечным ответом ячейки: для ответа вычисляется функция softmax, чтобы получить p — вероятности для выходных символов [1]. Я пользуюсь этими символами для единообразия с кодом min-char-rnn, хотя, вероятно, было бы более читабельно поменять местами p и y (сделать y фактическим выводом ячейки).

С математической точки зрения ячейка выполняет следующие расчёты:

Обучение параметров модели при помощи обратного распространения ошибки

Посмотрим, как изучить параметры W и b для нашей модели. В основном это стандартная процедура для нейросетей. Вычислим производные для всех итераций (steps), а затем реализуем обратное распространение ошибки, чтобы на основании расчёта потерь определить требуемое обновление параметров.

Но для этого сначала нужно разобраться с одной серьёзной проблемой. Обратное распространение ошибки обычно используют для ациклических графов, и непонятно, как применить его к нашей РНС. Значение h входное или выходное? Или и то, и другое? В начальной высокоуровневой диаграмме ячейки РНС h является и входным, и выходным значением — как нам рассчитать его градиент, если его значение пока неизвестно? [2]

Выход из этого тупика кроется в том, чтобы развернуть РНС на несколько итераций цикла. Отмечу, что мы уже сделали это в подробной схеме, разделив и . Это делает каждую ячейку РНС локально ациклической, что позволяет применить к ней обратное распространение. Название этого подхода звучит круто — обратное распространение ошибки во времени (BPTT, Backpropagation Through Time) — но на самом деле это то же самое, что и просто «обратное распространение».

Обратите внимание, что используемая здесь архитектура у Карпаты в статье Unreasonable Effectiveness of RNNs называется синхронизацией «многие ко многим» (synced many-to-many) и она полезна для символьно-ориентированного обучения простой языковой модели — мы сразу наблюдаем выходную последовательность, производимую моделью при чтении входных данных. Подобное разворачивание применимо и к другим архитектурам, например кодер — декодер.

Это снова наша РНС, развёрнутая в третьей итерации:

На этой диаграмме отметим градиентные потоки светло-коричневыми стрелками:

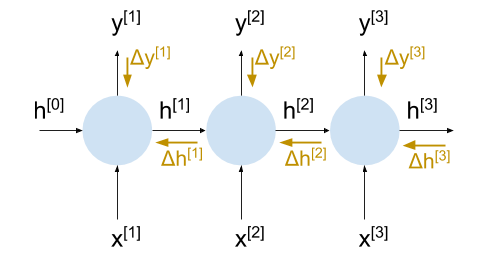
При таком разворачивании у нас есть всё необходимое для вычисления фактических изменений весовых коэффициентов в ходе обучения, потому что, когда мы хотим вычислить градиенты после второй итерации, у нас уже есть входящий градиент , и так далее.

Вам интересно, каково значение на последней итерации, в момент t?

В некоторых моделях длина последовательности достаточно ограниченна. Например, длина последовательности одного переводимого предложения редко превышает двадцать пять слов. Для таких моделей мы можем развернуть РНС полностью. Выходное состояние h на последней итерации на самом деле «никуда не пропадает», и мы предполагаем, что у него нулевой градиент. Входное состояние h для первой итерации тоже равно нулю по аналогичным причинам.

Другие модели работают с последовательностями потенциально бесконечной длины или с последовательностями, которые слишком длинны для разворачивания. Языковая модель в min-char-rnn — хороший тому пример, так как теоретически она может принимать и выдавать текст любой длины. Для этих моделей будем использовать усечённый BPTT, исходя из допущения, что влияние текущего состояния распространяется только на N итераций в будущее. Затем мы прокрутим модель N раз и предположим, что равна нулю. Хотя на самом деле это не так, для достаточно большого N это довольно надёжное предположение. РНС трудно обучать на очень длинных последовательностях по ряду других причин (мы ещё затронем эту тему в конце статьи).

Важно помнить, что, хотя мы и разворачиваем ячейки РНС, все параметры (весовые коэффициенты, смещения) остаются общими. Это важно для инвариантности преобразования моделей: изученные в одном месте паттерны должны быть применимы в другом месте [3]. Остаётся вопрос о том, как же нам обновить весовые коэффициенты, ведь мы рассчитываем градиенты для них отдельно на каждой итерации. Мы просто суммируем их. Как и в случае, когда вывод ячейки разветвляется на два направления, их значения при вычислении градиентов складываются вдоль ветвей — это обычное цепное правило в действии.

Теперь у нас есть всё необходимое для понимания принципов обучения РНС. Осталось выяснить, как градиенты распространяются внутри ячейки. Иными словами, каковы производные от каждой операции, которая содержится в ячейке.

Перетекание градиента внутри ячейки РНС

Формулы расчёта выходного значения ячейки по входным мы уже видели:

Для изучения весовых коэффициентов нужно сначала найти производные выходного значения ячейки для них. Сам процесс обратного распространения полностью описан в отдельной статье, поэтому здесь я ограничусь небольшой памяткой об этом.

Как мы помним, — прогнозируемое выходное значение (predicted output). Сравним его с «реальным» выходным значением () при обучении, чтобы найти потери (ошибку):

Чтобы выполнить обновление градиентного спуска, нам нужно найти для каждого значения весового коэффициента w. Чтобы это сделать, нужно:

1. Найти «локальные» градиенты каждой математической операции, которая ведёт от w к L.
2. Использовать цепное правило для обратного распространения ошибки по всем этим локальным градиентам, пока мы не найдём .

Для начала сформулируем цепное правило, чтобы вычислить :

Затем:

Пусть весовой коэффициент w, который нас интересует, входит в , тогда нам нужно произвести ещё некоторое распространение:

После этого мы проведём распространение через функцию tanh, сложение смещений и, наконец, умножение на , для которого производная по w вычисляется напрямую, без дальнейшего применения цепного правила.

Теперь посмотрим, как вычислить все соответствующие локальные градиенты.

Градиент потерь перекрёстной энтропии

Начнём с производной функции потерь, которая представляет собой кросс-энтропию в рамках модели min-char-rnn. Подробное выведение градиента softmax с последующей перекрёстной энтропией я рассмотрел в отдельной статье. Здесь привожу лишь краткий обзор:

Если переформулировать это для нашего частного случая, потери будут определяться функцией при допущении, что «реальный» класс r является постоянным для каждого обучающего примера:

Поскольку входы и выходы ячейки кодируются одним активным состоянием, будем использовать r для обозначения индекса, где r(k) ненулевой. Тогда якобиан L ненулевой только при индексе r и его значение равно

Градиент многопеременной логистической функции

Подробный расчёт градиента многопеременной логистической функции (softmax) представлен в отдельной статье. Для функции S(y), которая является многопеременной логистической функцией y, якобиан будет:

Градиент полносвязного слоя

Продолжим наше обратное распространение так:

$$display$$y^{[t]}&=W_{hy}\cdot h^{[t]}+b_y$$display$$

Как я указал в статье про обратное распространение через полносвязный слой, . Но это ещё не всё. Обратите внимание, что при прямом проходе h^{[t]} делится на две части (edges): одна подходит к полносвязному слою, а другая — к следующей ячейке РНС в качестве состояния (state). При обратном распространении градиента потерь на мы должны учитывать обе части. Точнее, нам нужно добавить градиенты для обеих частей. В результате мы получаем следующее уравнение обратного распространения:

Обратите внимание, что этот слой уже имеет параметры модели для изучения: и — «конечная станция» обратного распространения. Пожалуйста, посмотрите мою статью про обратное распространение через полносвязный слой, чтобы узнать, как вычислить градиенты этих параметров.

Градиент tanh

Вектор образуется при применении гиперболической тангенциальной нелинейности к другому полносвязному слою.

$$display$$h^{[t]}&=tanh(W_{hh}\cdot h^{[t-1]}+W_{xh}\cdot x^{[t]}+b_h)$$display$$

Чтобы получить параметры модели , и , нам сначала нужно выполнить обратное распространение градиента потерь через tanh. tanh — скалярная функция. Если мы применяем её к вектору, мы делаем это поэлементно и независимо для каждого элемента вектора. При этом мы собираем результаты в аналогичный по форме вектор результатов.

Математическое определение выглядит так:

Чтобы найти производную этой функции, применим формулу для выведения соотношения:

Тогда:

Как и для многопеременной логистической функции, оказывается, что существует удобный способ выразить производную tanh в понятиях самой tanh. Когда мы применяем цепное правило к производным tanh, например: h=tanh(k), где k — функция от w. Мы получаем:

В нашем случае k(w) — полносвязный слой. Чтобы найти его производные для матриц весовых коэффициентов и смещение, пожалуйста, обратитесь к статье про обратное распространение через полносвязный слой.

Изучение параметров модели при помощи Adagrad

Мы только что прошли по всем важнейшим частям ячейки РНС и вычислили локальные градиенты. Вооружённые этими формулами и цепным правилом, мы должны понять, как код min-char-rnn вычисляет градиент потерь в обратном направлении. Но это ещё не конец; как только мы получили производные потерь для некоторого параметра модели, как нам обновить этот параметр?

Самое простое, что можно сделать, — использовать алгоритм градиентного спуска с некоторой постоянной скоростью обучения. О градиентном спуске я писал отдельную статью — пожалуйста, загляните в неё, чтобы освежить в памяти этот материал.

В наши дни основная часть изучения объектов реального мира (real-world learning) опирается на более совершенные алгоритмы. Один из таких алгоритмов называется Adagrad. Его предложили в 2011 году эксперты по математической оптимизации. Кстати, min-char-rnn использует Adagrad, поэтому упрощённо объясню принцип его работы.

Основная мысль состоит в регулировке скорости обучения для каждого параметра по отдельности, поскольку на практике одни параметры меняются гораздо чаще других. Это может быть связано с редкими примерами в наборе обучающих данных, влияющих на параметр, который нечасто подвергается изменениям. Поскольку эти изменения редки, мы хотим усилить их. Изменения параметров, которые меняются чаще, мы хотим, наоборот, «приглушить».

Поэтому алгоритм Adagrad работает так:

# Same shape as the parameter array x
memory = 0
while True:
  dx = compute_grad(x)

  # Elementwise: each memory element gets the corresponding dx^2 added to it.
  memory += dx * dx

  # The actual parameter update for this step. Note how the learning rate is
  # modified by the memory. epsilon is some very small number to avoid dividing
  # by 0.
  x -= learning_rate * dx / (np.sqrt(memory) + epsilon)

Если заданный элемент в dx значительно обновлён в прошлом, соответствующий элемент памяти будет расти, и, таким образом, скорость обучения эффективно снижается.

Отсечение градиентов

Если мы развернём ячейку РНС 10 раз, градиент умножится на десять раз на протяжении всего пути от последней ячейки к первой. Для некоторых структур это может привести к эффекту «взрывного градиента», при котором значение продолжает расти [4].

Чтобы смягчить этот эффект, в min-char-rnn при каждом обновлении градиенты «отсекаются» до некоторого разумного диапазона (например, от -5 до 5), чтобы они никогда не вышли за пределы этого диапазона. Это грубый метод, но он довольно хорошо подходит для обучения РНС.

Обратная проблема исчезающих градиентов (когда градиенты становятся всё меньше с каждой итерацией) решается сложнее. Для такого решения обычно требуются более совершенные архитектуры РНС.

Качество модели min-char-rnn

Хотя min-char-rnn является полной реализацией РНС, которая умеет обучаться, она не подходит для обучения разумной модели английского языка. Модель слишком проста для этого и сильно страдает от проблемы исчезающего градиента.

Например, при изучении развёрнутой модели на 16 итераций на примере корпуса книг о Шерлоке Холмсе после 60 000 итераций (обучение на примерно 1 Мб текста) она выдаёт довольно бессмысленный текст:

one, my dred, roriny. qued bamp gond hilves non froange saws, to mold his a work, you shirs larcs anverver strepule thunboler muste, thum and cormed sightourd so was rewa her besee pilman

Этот текст, конечно, не стопроцентная тарабарщина, но до настоящего английского ему далеко. Ради развлечения я написал несложный генератор цепей Маркова и обучил его на том же тексте, за состояние я взял 4 символа. Вот что получилось на выходе:

though throughted with to taken as when it diabolice, and intered the stairhead, the stood initions of indeed, as burst, his mr. holmes' room, and now i fellows. the stable. he retails arm

Согласитесь, уже куда лучше, чем результат модного подхода — глубокого обучения! Да и обучение стало проходить быстрее…

Чтобы с большей вероятностью обучить модель хорошо, нам понадобится более совершенная архитектура, например LSTM. Для сохранения долгосрочных зависимостей между ячейками в LSTM используется немало уловок. Это заметно повышает качество обучения моделей. Например, модель Андрея Карпаты char-rnn из статьи Unreasonable Effectiveness of RNNs является многослойной LSTM и довольно хорошо может обучать модели из различных областей, от сонетов Шекспира до сниппетов кода на C в ядре Linux.

Заключение

В этой статье я не стремился построить очень хорошую модель РНС. Скорее, я хотел подробно объяснить математику обучения простой РНС. Более продвинутые архитектуры РНС, такие как LSTM, несколько сложнее, но все ключевые идеи довольно схожи, поэтому эта статья будет полезна для изучения азов.

Обновление: Расширение этой статьи для LSTM.

---

[1]

Расчёт многопеременной логистической функции (softmax) имеет смысл, поскольку x кодируется одним активным состоянием (one-hot) на векторе, размер которого соответствует размеру всего словаря. Таким образом, в позиции обозначаемой буквы стоит 1, а во всех остальных позициях — 0. Например, если нас интересуют лишь 26 букв латинского алфавита в нижнем регистре, x может быть вектором длиной в 26 элементов. У буквы 'a' в положении 0 будет стоять единица, а в остальных — нули, а у буквы 'd' единственная единица будет стоять в положении 3.

Выход p здесь моделирует то, каким, с точки зрения ячейки РНС, должен быть следующий генерируемый символ. При использовании softmax, он будет иметь вероятности для каждого символа в соответствующей позиции, все они будут суммироваться до 1.

[2]

Немного более техническое объяснение: чтобы вычислить градиент ошибки для весовых коэффициентов в типичном потоке обратного распространения, нам потребуются входные градиенты для p[t] и h[t]. Затем, при обучении, мы используем измеренную ошибку и распространим её в обратном направлении. Но какова ошибка измерения h[t]? Мы не узнаем её, пока не вычислим ошибку следующей итерации, и наоборот — это немного похоже на задачу про курицу и яйцо.

Развёртывание/BPTT позволяет найти приблизительное решение этой задачи. Альтернатива — распространение градиента в прямом направлении (forward-mode gradient propagation). При этом используется алгоритм, который называется обучением с обратной связью в реальном времени (RTRL, Real Time Recurrent Learning). Этот алгоритм хорошо работает, но имеет большие вычислительные затраты, чем BPTT. Я бы очень хотел рассмотреть эту тему подробнее, поскольку она связана с разницей между прямым и обратным автоматическим дифференцированием. Однако эта тема заслуживает отдельной статьи.

[3]

Это похоже на работу свёрточных сетей, где весовые коэффициенты фильтра свёртки используются многократно при обработке гораздо большего входного материала. В таких моделях инвариантность является пространственной, а в моделях последовательности — временной. В действительности, соотношение пространства и времени в моделях — это лишь условность, и оказывается, что одномерные свёрточные модели отлично справляются с некоторыми задачами, касающимися последовательности!

[4]

Это проще всего представить себе так: некоторое начальное значение v многократно умножается на другое значение c. При N умножениях мы получаем vc^N. Если c больше 1, результат будет расти с каждым умножением. Скорость его роста зависит от фактического значения c, но, как правило, это экспоненциальный сток (exponential runoff). Нам, разумеется, интересно реальное значение c, так как сток работает одинаково плохо для положительного и отрицательного направления.

Аналогично, если абсолютное значение c меньше 1, мы получим эффект «исчезновения», поскольку результат будет уменьшаться с каждой итерацией.

А мы научим вас аккуратно работать с данными, чтобы вы прокачали карьеру и стали востребованным IT-специалистом. Если вы не найдёте работу, мы просто вернём деньги (возврат — акция в рамках «Чёрной пятницы»).

• Профессия Data Scientist (24 месяца)
• Профессия Data Analyst (10 месяцев)