SIMATIC WinCC Open Architecture – это SCADA система разработки ETM(Siemens). В последние годы стала достаточно популярна в России в определенных кругах.

Поскольку в интернете информации о данном продукте не очень много, а на обучениях даются достаточно поверхностные знания и многие моменты не затрагиваются, появилась идея попробовать написать серию статей с интересными на мой взгляд темами.

В WinCC OA встроен C/C++ подобный скриптовый язык CONTROL. О его возможностях сегодня и поговорим.

Динамические массивы

Динамические массивы представлены двумя видами типов данных:

• vector<type>, где type – тип данных. Тип может быть простым как int или double, так и сложным как строка, структура или же другой вектор. По сути, это тот же вектор, как и в C++ с похожими методами и возможностями.

• Динамический массив Dyn_type, где type также тип данных.

В целом оба вида принципиально ничем не отличаются. В документации так дословно сказано об их различиях:

The biggest difference between vectors and dyn_ variables is the index. For vectors this index starts at 0 while dyn_ variables start at 1

Тут также стоит отметить, что возможен такой вариант как vector<void>. В документации про это написано следующее:

The void data type for a vector allows to add any data type. A vector<void> is similar to a dyn_anytype, but a dyn_anytype is a dyn_ containing anytype variables, which themselves point to any other type. In terms of performance and memory consumption, the vector<void> is better, since it directly holds the final pointers to whatever datatype was given.

Объект вектора и динамического массива имеют одинаковые методы:

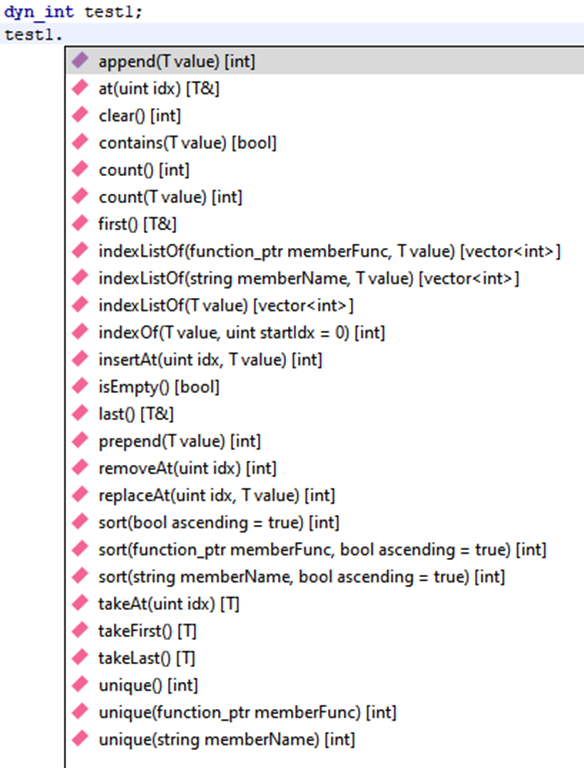
Также в языке предусмотрены отдельные функции для работы с динамическими массивами. Такие функции использовать с вектором не получится.

Перечень функций из документации:

Ассоциативные массивы

Этот тип данных представлен одним видом: «mapping».

Из документации:

Переменные "mapping" сохраняют произвольные пары ключ-значение. Ключи и значения сохраняются в два массива: один для ключей и один для значений

Таким обозом получается, что тут мы имеем дело с самой простой реализацией и «под капотом» у нас два массива. Попахивает линейной сложностью O(n) выполнения основных операций добавления, поиска и удаления. Никаких тут тебе двоичных деревьев поиска и хеш-таблиц с их логарифмическими O(log n) и константными O(1) сложностями.

Методы ассоциативного массива:

Функции для работы с mapping:

Строки

Отдельно стоит отметить наличие такого типа данных как строка: string. По сути, это массив с элементами типа char. Индексирование как и у вектора начинается с 0. Каждый символ можно считать при помощи оператора []. Но тут надо быть осторожным. Строки не могут быть записаны или перезаписаны посимвольно. В остальном со строками удобно работать. Для них реализовано большое количество удобных функций.

Методы строки:

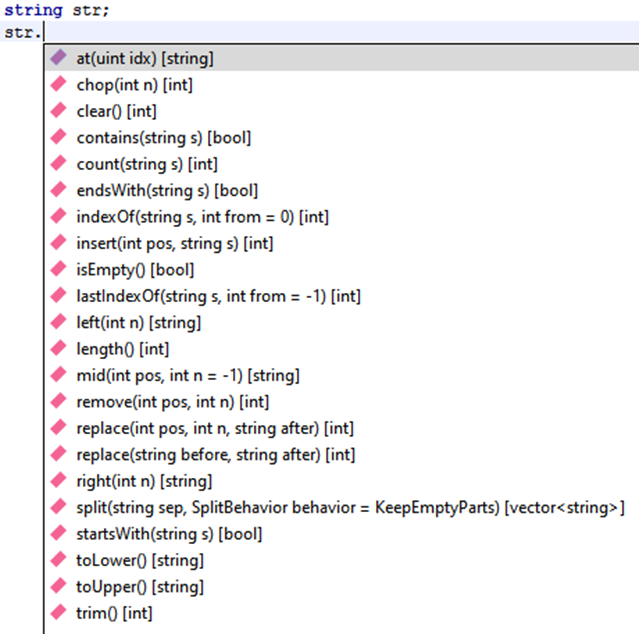
Функции для работы со строками

На этом с контейнерными типами данных все, но этого вполне достаточно, чтобы реализовать другие, учитывая наличие такого удобного инструмента как умный указатель shared_ptr.

Для начала начнем с чего-нибудь попроще, а именно с приоритетной очереди. Вдохновение будем черпать у priority_queue из стандартной библиотеки C++.

Приоритетная очередь (priority queue) или Бинарная куча (Heap)

Данную структуру данных реализовывают в виде пирамиды, где в корне находится элемент с наибольшим приоритетом.

Пирамиду удобно сделать на массиве. Для этого будем использовать следующие правила:

• индекс корня дерева равен 1

• нулевой индекс массива не используем. Это нужно для удобства расчета остальных индексов дерева

• индекс левого потомка для родителя i равен 2*i

• индекс правого потомка для родителя i равен 2*i + 1

• индекс родителя для потомка i равен целочисленному делению i на 2

Массив:

Попробуем реализовать класс PriorityQueue. Тут здравый смысл говорит, что класс должен быть шаблонным, но в WinCC OA такого понятия нет. Выйти из этой ситуации нам помогут типы данных vector<void> и anytype.

В качестве полей класса запишем вектор, который будет хранить нашу пирамиду, отдельно чисто для сомнительного удобства будем хранить размер кучи и указатель на функцию компаратор. Благо наличие такого указателя разработчики WinCC OA предусмотрели.

Кратко об этом из документации:

Идем дальше. Конструктор будет инициализировать поля класса начальными значениями. Для дефолтного значения указателя на компаратор реализуем приватный метод DefaultComp.

Также реализуем методы:

• Top  – выводит элемент очереди с наибольшим приоритетом (элемент вектора с индексом 1)

• Empty – проверка очереди на пустоту

• Size – выводит размер очереди

• Swap – меняет местами две очереди. Тут для удобства дополнительно реализуем приватный метод Sw

  Получаем такой код:

class PriorityQueue {
  private vector<void> heap_;
  private int size_;
  private function_ptr comp_;

  //The compare function must be declared static.
  public PriorityQueue(function_ptr compare = DefaultComp){
    size_ = 0;
    heap_.append(0);
    comp_ = compare;
  }

  //accesses the top element
  public anytype Top(){
    return heap_.at(1);
  }

  //checks whether the underlying container is empty
  public bool Empty(){
    return size_ == 0;
  }

  //returns the number of elements
  public int Size(){
    return size_;
  }

  //swaps the contents
  public Swap(PriorityQueue& other){
    Sw(size_, other.size_);
    Sw(comp_, other.comp_);
    Sw(heap_, other.heap_);
  }

  private Sw(anytype& lhs, anytype& rhs){
    anytype temp = lhs;
    lhs = rhs;
    rhs = temp;
  }

  private static bool DefaultComp(const anytype lhs, const anytype rhs) {
    return lhs < rhs;
  }
};

Вставка элемента

Вставку нового элемента будем осуществлять следующим образом. Элемент добавляем в конец кучи, т.е. в конец нашего массива.

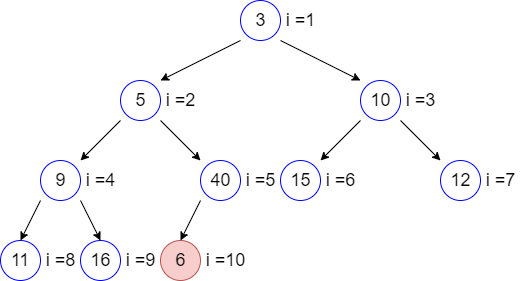
Массив:

Далее нам надо сделать так называемое «просеивание вверх», чтобы новый элемент занял свое место в очереди в соответствии со своим значением. Такая вставка будет происходить за O(log n).

Массив:

 Попробуем реализовать. Для этого добавим в класс PriorityQueue следующие методы:

• Push – вставка нового элемента

• SiftUp – просеивание вверх выделим в отдельный приватный метод

Код:

//inserts element and sorts the underlying container
public Push(anytype item){
  heap_.append(item);
  ++size_;
  SiftUp();
}

private SiftUp() {
  int idx = Size();
  while (true) {
    if (idx == 1) {
      break;
    }
        
    if (callFunction(comp_, heap_[idx], heap_[idx / 2])) {
      Sw(heap_[idx], heap_[idx / 2]);
      idx /= 2;
    }
    else {
      break;
    }
  }
}

Удаление элемента

Удаление элемента осуществляется из корня нашей пирамиды. Чтобы дерево при этом не распалось мы это место затыкаем последним элементом массива, перенеся его в ячейку i=1.

Массив:

После этого нам необходимо сделать «просеивание вниз», чтобы на вершине снова появился элемент с наивысшим приоритетом и все элементы кучи заняли свои места. Такое удаление будет происходить за O(log n).

Массив:

Реализуем. Для этого добавим в класс PriorityQueue следующие методы:

• Pop – удаление элемента с наибольшим приоритетом

• TakeTop – выводит элемент с наибольшим приоритетом одновременно удаляя его из очереди

• SiftDown – просеивание вниз выделим в отдельный приватный метод

Код:

//removes the top element
public Pop(){
  if (Size() > 1) {
    heap_[1] = heap_.takeLast();
    --size_;
    SiftDown();
  }
  else if(Size() == 1) {
    heap_.removeAt(1);
    --size_;
  }
}
  
public anytype TakeTop(){
  anytype temp = heap_.at(1);
  Pop();
  return temp;
}

private SiftDown() {
  int idx = 1;
  while (true) {
    if (heap_.count() > 2 * idx + 1) {
      if (callFunction(comp_, heap_[2 * idx], heap_[2 * idx + 1])) {
        if (callFunction(comp_, heap_[2 * idx], heap_[idx])) {
          Sw(heap_[2 * idx], heap_[idx]);
          idx = 2 * idx;
        }
        else {
          break;
        }
      }
      else {
        if (callFunction(comp_, heap_[2 * idx + 1], heap_[idx])) {
          Sw(heap_[2 * idx + 1], heap_[idx]);
          idx = 2 * idx + 1;
        }
        else {
          break;
        }
      }
    }
    else if (heap_.count() == 2 * idx + 1 && callFunction(comp_, heap_[2 * idx], heap_[idx])) {
      Sw(heap_[2 * idx], heap_[idx]);
      break;
    }
    else {
      break;
    }
  }
}

Вишенка на торте

Для удобства установки приоритета создадим небольшой класс CompareClass

class CompareClass
{
  public static bool Greater(const anytype& lhs, const anytype& rhs) {
    return lhs > rhs;
  }

  public static bool Less(const anytype& lhs, const anytype& rhs) {
    return lhs < rhs;
  }
};

Таким образом сможем провести небольшое тестирование получившейся приоритетной очереди

void UnitTestPriorityQueue() {
    function_ptr ptr_greater = CompareClass::Greater;
    PriorityQueue pq = PriorityQueue(ptr_greater);

    oaUnitAssertEqual("TestCase №1", pq.Size(), 0);
    oaUnitAssertTrue("TestCase №2", pq.Empty());
    pq.Push(10);
    oaUnitAssertEqual("TestCase №3", pq.Top(), 10);
    pq.Push(4);
    oaUnitAssertEqual("TestCase №4", pq.Top(), 10);
    pq.Push(15);
    oaUnitAssertEqual("TestCase №5", pq.Top(), 15);
    pq.Push(6);
    oaUnitAssertEqual("TestCase №6", pq.Top(), 15);
    pq.Push(3);
    oaUnitAssertEqual("TestCase №7", pq.Top(), 15);
    pq.Push(20);
    oaUnitAssertEqual("TestCase №8", pq.Top(), 20);
    pq.Push(7);
    oaUnitAssertEqual("TestCase №9", pq.Top(), 20);
    oaUnitAssertEqual("TestCase №10", pq.Size(), 7);
    pq.Pop();
    oaUnitAssertEqual("TestCase №11", pq.Top(), 15);
    oaUnitAssertEqual("TestCase №12", pq.Size(), 6);
    oaUnitAssertEqual("TestCase №13", pq.TakeTop(), 15);
    oaUnitAssertEqual("TestCase №14", pq.Top(), 10);
    oaUnitAssertEqual("TestCase №16", pq.Size(), 5);

    while(!pq.Empty()) {
      pq.Pop();
    }

    oaUnitAssertEqual("TestCase №16", pq.Size(), 0);
}

Продолжение следует… но это не точно :)