На протяжении последних шести лет я участвовал в исследованиях, посвященных моделированию стационарных и нестационарных температурных полей активных зон ядерных реакторов. Среди довольно полезных для ядерной энергетики результатов я бы хотел выделить главный – выявление способности уравнения теплопроводности сплошной среды достаточно точно описать стационарные и нестационарные температурные поля активных зон гетерогенных ядерных реакторов, таких как Pressurized water reactor (PWR) и Gas turbine modular helium reactor (GT-MHR).

О чем идет речь?

Ядерный реактор – по своей сути является источником тепла, который нужно охлаждать. Охлаждение реактора происходит при течении теплоносителя через его активную зону. Активная зона — это центральное место в реакторе, в котором происходит деление ядерного топлива и выделение тепла. Для моделирования процессов, связанных с течением жидкости, используется вычислительная гидродинамика – Computational fluid dynamics (CFD).

В основе CFD моделирования лежит система уравнений тепломасообмена, которая состоит из уравнения теплопроводности (энергии), уравнения неразрывности и уравнений Навье-Стокса вместе с замыкающими уравнениями, описывающими некоторую модель турбулентности.

Для получения адекватного результата моделирование течения жидкости требует максимально подробной формулировки условий течения, то есть следует как можно более развернуто описать расчетную область. Это приводит к необходимости располагать огромными вычислительными мощностями.

А можно ли обойтись без суперкомпьютеров?

Что касается моделирования активной зоны, то ответ – нет. Но в некоторых случаях да. О чем, собственно, и статья.

В связи с отсутствием возможности смоделировать течение теплоносителя через всю активную зону, все проведенные исследования основывались на моделях реальных объектов.

Давайте рассмотрим одну такую модель-фрагмент активной зоны реактора типа PWR при CFD моделировании.

Расчетную модель активной зоны представим как ряд примыкающих друг к другу твэлов, расположенных по диаметральной линии поперечного сечения активной зоны. Всю совокупность твэлов считаем теплоизолированной по боковым границам. Скорость теплоносителя на короткой боковой границе равна нулю. На длинной боковой границе – максимальные для каждого твэла значения скоростей.

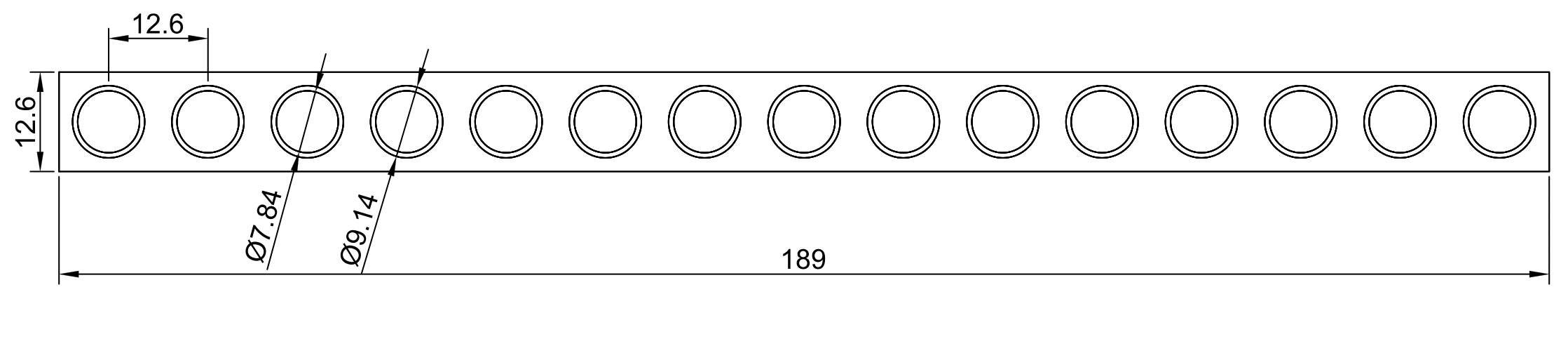
Заметим, что принятая модель отражает радиальную симметрию тепловых и гидродинамических процессов в реальной активной зоне.

Сетка этой модели содержит 2083554 элементов и 2162712 узлов.

В чем заключается авторский подход?

Как оказалось, уравнение теплопроводности вполне способно описать температурное поле представленного выше фрагмента активной зоны. Это означает, что классическая система уравнений тепломассообмена лишается таких уравнений, как уравнения Навье-Стокса вместе с уравнениями, описывающими некоторую модель турбулентности.

Исключение этих уравнений приводит к очень серьезному упрощению сетки модели со снижением числа расчетных элементов. Иными словами, рассматриваемая активная зона в виде сложной пространственной системы, состоящей из теплоносителя и твэлов, заменяется на однородное твердое тело, условно разделенное на ячейки.

При использовании только модифицированного уравнения теплопроводности, расчетную область можно представить, как некоторый квадрат со стороной 17 элементов. В итоге имеем 289 элементов. А это в 7210 раз меньше, чем при использовании CFD!

Как именно было модифицировано уравнение теплопроводности?

Как уже было сказано, главной отличительной чертой нового подхода является использование в численном методе расчета лишь одного уравнения – уравнения теплопроводности.

В основе подхода лежит уравнение теплопроводности в виде:

При этом температуры Т связаны со средними по элементарному объёму температурами теплоносителя Т₂, оболочки твэла T_sh и топливного стержня (таблеток) T_f через соответствующие доли материалов в ячейке:

Для анализа переходных процессов также выполнен вывод расчетных зависимостей, таких как соотношения для определения тепломассообмена между твэлами, получена модель эффективной теплопроводности λ_е.

Само по себе представленное уравнение теплопроводности не привносит ничего нового. «Магия» заключается в функции стока тепла q_v.st. Смысл этой функции заключается в имитации эффектов от течения теплоносителя через активную зону.

здесь: σ = F/V; F – теплообменная поверхность единичного твэла, м²; V – объём расчетной ячейки, м³; q⁰ – плотность теплового потока на единицу поверхности твэла, Вт/м². Индекс «0» - стационарное (некоторое исходное состояние); f – функция времени, пространственных координат и возмущающих воздействий; P – функция, отражающая влияние граничных условий.

На основе представленных уравнений был разработан алгоритм быстрого расчета стационарных и нестационарных температурных полей.

Насколько точно авторский подход описывает температурные поля?

На рисунках 4 и 5 представлены некоторые результаты расчетов изменений полей средневзвешенных температур после внесения скачкообразных возмущений в стационарную работу реактора в исследуемой активной зоной (рисунки 1-3). Рассматривалось комплексное возмущение и возмущение по одному параметру – по тепловой мощности реактора. Комплексное возмущение – одновременное изменение мощности реактора, температуры на входе в активную зону и расхода теплоносителя, а также коэффициента теплоотдачи, согласованного с изменением названных параметров.

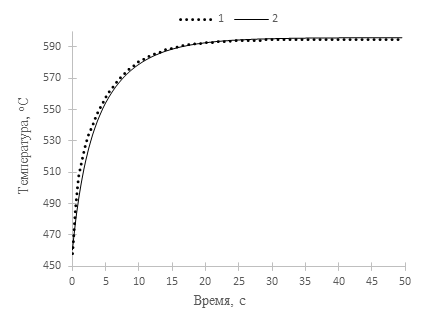
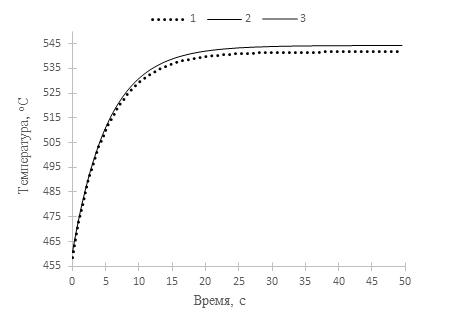
Распределение средневзвешенной температуры (рисунок 6) в модели активной зоны было рассчитано методом установления по неявной конечно-разностной схеме решения представленного уравнения теплопроводности

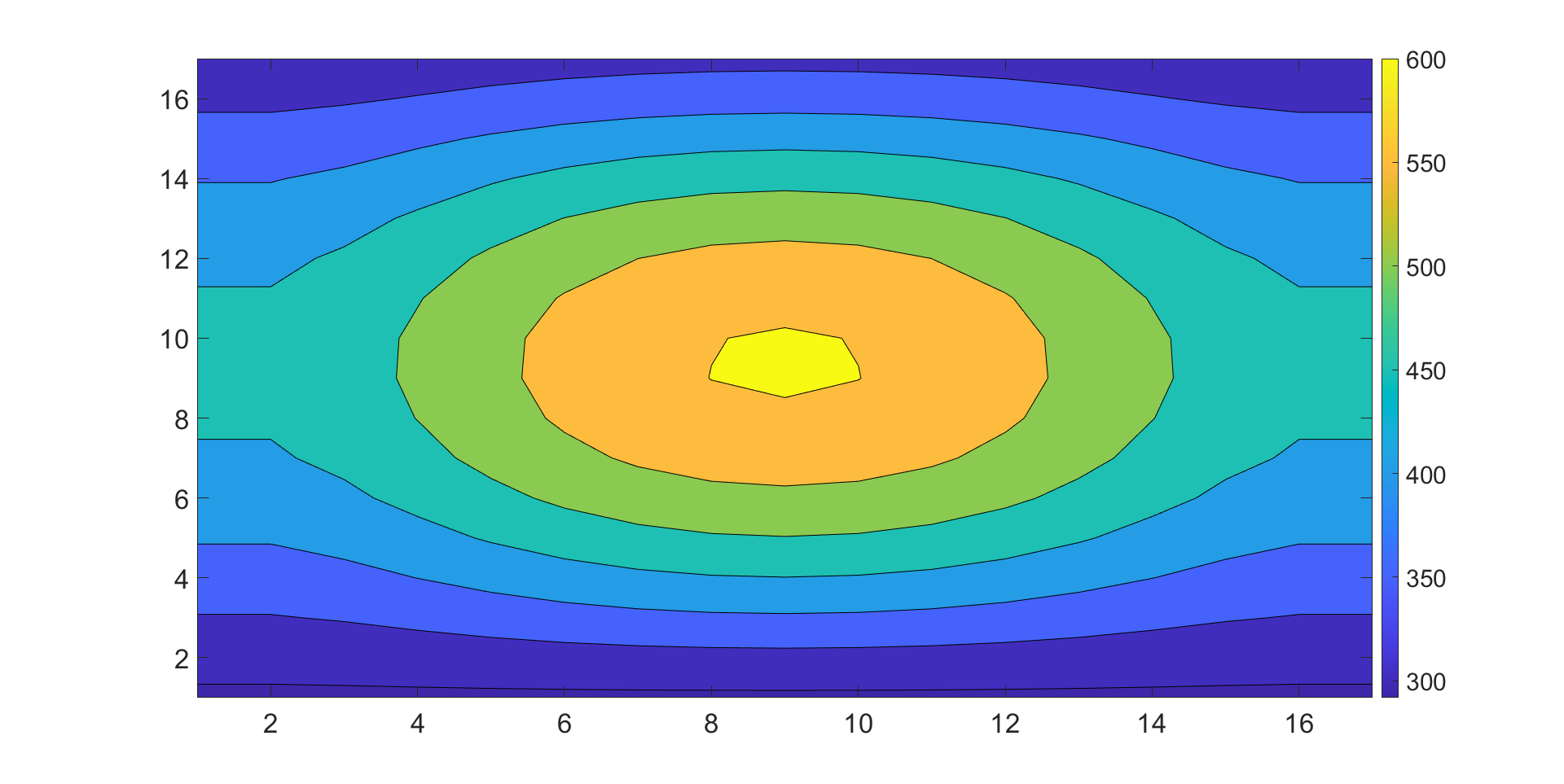
Сравнение результатов, полученных по авторской программе, с результатами CFD моделирования по установившимся (после нанесенного возмущения) значениям средневзвешенной температуры показывают вполне удовлетворительное совпадение: отклонение температуры не превышает 0.5% (2.2 ^оС).

Пара слов о реализации данного алгоритма и CFD моделировании

Достоверность результатов, полученных по предложенным зависимостям, была подтверждена путем сравнения с расчетами программной системы конечно-элементного анализа ANSYS Fluent.

Энерговыделение в твэлах имеет косинусоидальный профиль по высоте. По радиусу мощность твэлов меняется в соответствии с коэффициентом неравномерности, соответствующим реальной активной зоне реактора типа PWR. Для реализации этих условий в ANSYS Fluent были написаны user defined functions – UDF.

Изначально алгоритм был реализован в среде Mathcad. В Mathcad скорость расчета температурных полей оставляла желать лучшего, хотя и была сопоставима со временем, с которым протекает процесс перестройки температурного поля в исследуемом фрагменте активной зоны. Впоследствии алгоритм был перенесен на Java. Java была выбрана потому, что в ней нет необходимости работать с памятью напрямую, приложения получаются кроссплатформенными и самое важное – наличие многопоточности. И, по моему личному мнению, Java обладает приятным синтаксисом.

Несмотря на то, что программы, написанные на Java, не самые быстрые, полученная реализация алгоритма оказалась очень эффективна. На рисунках 4-5 видно, что для рассматриваемого фрагмента активной зоны время переходного процесса составляет примерно 25 секунд, в то время как расчет Java программы занимает около одной секунды.

Такое быстродействие дает возможность для базового фрагмента активной зоны предсказывать последствия по изменению температурного поля практически при нанесении возмущения.

Итог

В результате научной работы был разработан алгоритм, на основе которого создана программа расчета температурного поля в реакторах разного типа в переходных режимах. Программа расчета верифицирована путем сравнения результатов многочисленных расчетов с CFD моделированием соответствующих переходных процессов. Преимуществом созданной программы является возможность расчета изменения состояния активных зон в режиме реального времени, что позволяет использовать программу при расчетах переходных процессов в контурах ядерных энергетических установок в целом, в частности при создании тренажеров. Продемонстрирована работоспособность программы для анализа переходных процессов в активной зоне реактора типа PWR с покомпонентной детализацией температурного поля в расчетных ячейках.