Машина Тьюринга и машина состояний, детерминированный и недетерминированный конечный автомат, конечный автомат Мура и конечный автомат Мили. Голова кругом от всех этих понятий. Как во всем этом разобраться новичку? Тем более, что и у бывалых спецов бывает такая каша в голове из этих понятий. Чего только стоит вебинар от Яндекс Практикум на тему «Конечные автоматы в реальной жизни». Именно случайный просмотр этого вебинара сподвиг меня написать статью. Я обратил внимание, что даже более опытные лекторы ловко жонглируют всеми этими понятиями или подменяют одни другими в своих лекциях. С этим можно просто смириться, или дойти до безумия, разбираясь что к чему. И как со всем этим жить начинающему ардуинщику, если про конечные автоматы в программировании трубят из каждого утюга, а добраться до истины самостоятельно непросто?
Не гарантирую, что после прочтения статьи все сразу станет на свои места, но, как минимум, постараемся выудить из всей этой «каши» что-то полезное для себя. Так что усаживайтесь по удобнее, тема не простая, под катом будет много текста.
❯ Во всем виноваты математики
Да, именно так. Математика — это наука с долгой историей. Наука очень увлекательная, и поэтому она затягивает все большее количество умов. И каждому математику в душе хочется стать новым Пифагором, Евклидом, Лобачевским. А для этого необходимо постоянно расширять поле деятельности. Как только появляется какое-то новое научное направления, математики тут же жадно накидываются на него и изобретают свои новые теории.
Язык у математиков весьма своеобразный, совершенно непредназначенный для того, чтобы на нем разговаривать. Вот почему неподготовленному человеку в этих теориях сложно разобраться. К тому же, новые теории всегда строятся на уже имеющихся, происходит заимствование знакомых ранее понятий и адаптация их к новым условиям. От того путаницы становится все больше, остается ждать, пока все это как следует устоится.
Такая же участь ждала и электронику на заре ее развития. На ранних парах электроника была нераздельно связана со словом «радио» (радиоэлектроника), и ориентирована на радиосвязь. Новое прикладное применение обрела для себя тригонометрия, подтянулась теория сигналов, преобразования Фурье и еще много чего интересного.
❯ Комбинационные логические схемы
С развитием электроники от нее стали откалываться новые направления. Одно из таких — вычислительная техника. И тут математики тоже не остались в стороне. Хорошим подспорьем стала дискретная математика, от которой перешли к математической теории вычислительной техники.
К компьютерам вычислительная техника пришла далеко не сразу. Сперва появились комбинационные логические схемы. К таким схема можно отнести знакомые всем базовые логические вентили НЕ, И, ИЛИ, Исключающее ИЛИ и другие их комбинации. Шифраторы и дешифраторы можно считать более сложным вариантом комбинационных схем.
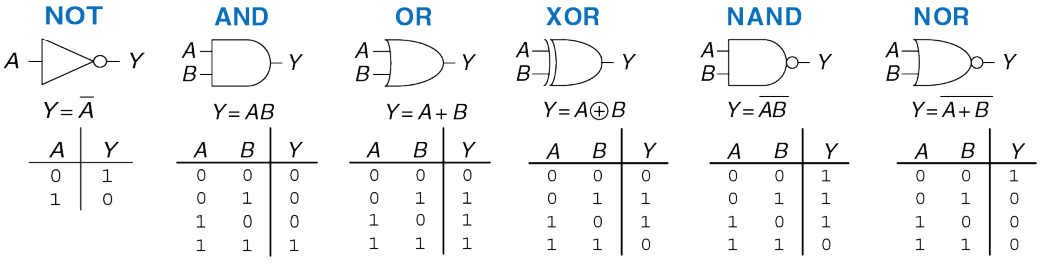
Особенность комбинационных схем заключается в том, что значение на выходе схемы зависит только от комбинации входных сигналов в текущий момент времени. Такие схемы не пригодны для сложных применений, так как не имеют элементов памяти. Описание работы комбинационных схем может быть выполнено в виде таблицы истинности или в виде логического выражения.
❯ Последовательностные логические схемы
Для реализации более сложных вычислений появились последовательностные логические схемы, значения на выходе которых зависят как от текущих входных значений, так и от предыдущих. Для этого последовательностные логические схемы содержат память. Эти схемы могут явно запоминать предыдущие значения определенных входов, или могут сжимать их в меньшее количество информации, называемое состоянием системы. Состояние системы содержит всю необходимую информацию о прошлом, необходимую для определения будущего поведения схемы.
В общем случае к последовательностным схемам можно отнести все схемы, которые не являются комбинационными. То есть последовательностные логические схемы – это те, значение выхода которых нельзя однозначно определить, зная лишь текущие значения входов.

Примером последовательностных логических схем могут служить защелки или различные типы триггеров. Они способны запоминать всего один бит информации. Объединение нескольких триггеров позволяет получить более сложные схемы параллельных, параллельно-последовательных, последовательно-параллельных и прочих регистров, которые способны хранить уже несколько бит.
❯ Конечный автомат Мура и Мили
Поведение некоторых последовательностных схем может быть весьма сложным, для описания их работы простые таблицы истинности уже не подходят. Чтобы упростить анализ сложных последовательностных логических схем, появилась теория цифровых автоматов для построения математических моделей, использующая понятие абстрактный автомат (Abstract Machine).
Абстрактный автомат — это математическая абстрактная модель дискретного устройства, имеющего один вход и один выход, в каждый момент находится в одном состоянии из множества возможных.
Частным случаем этой теории являются автоматы Мура и Мили, позволяющие описать функционирование цифровых систем, которые нашла широкое применение для синтеза сложных последовательностных схем на основе ПЛИС. А математические «иероглифы», которыми обильно сдобрена теория, стали хорошим подспорьем для языков описания аппаратуры подобных SystemVerilog или VHDL.
Автоматы Мура и Мили названы в честь своих изобретателей, ученых, разработавших теорию автоматов и математическую базу для них в фирме Bell Labs.

Эдвард Форест Мур (1925–2003) опубликовал свою первую статью «Gedankenexperiments on Sequential Machines» («Мысленные эксперименты с последовательностными автоматами») в 1956 году.

Джордж Мили (1927–2010) опубликовал «Method of Synthesizing Sequential Circuits» («Метод синтеза последовательностных схем») в 1955 году. Впоследствии он написал первую операционную систему для компьютера IBM 704. Позже он перешел на работу в Гарвардский Университет.

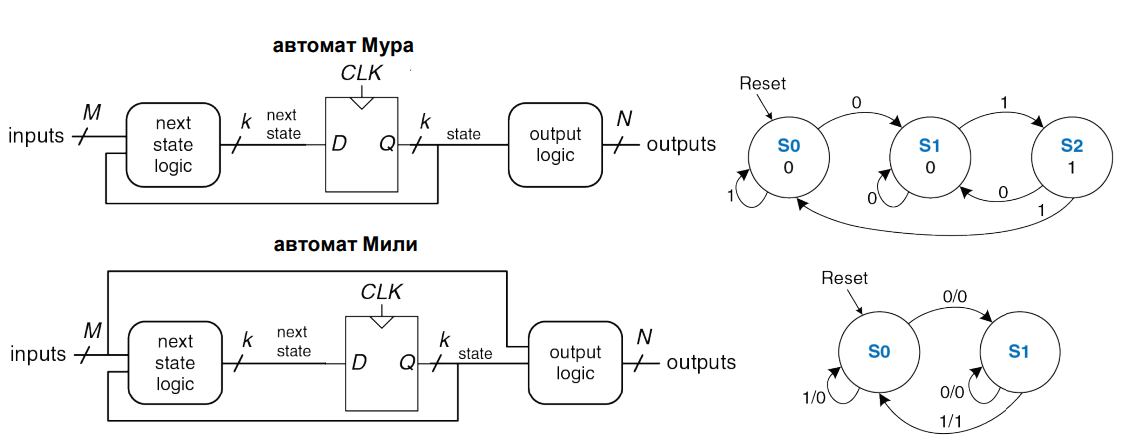
Схема конечного автомата содержит память для запоминания допустимых состояний. Выход схемы памяти вместе с входным сигналом поступает на входную схему формирования переходов, которая формирует новое значение в ячейке памяти (определяет следующее состояние). Также выход схемы памяти формирует выходной сигнал.
Если выходной сигнал полностью определяется значением ячейки памяти, то схему называют автомат Мура.
В ряде случаев в формировании выходного сигнала может задействоваться не только ячейка памяти, но и входной сигнал. Это позволяет сократить количество необходимых состояний. Такая схема называется автомат Мили.
Основная разница между конечными автоматами Мура и Мили в том, что у автомата Мура обычно больше (Moore – more) состояний, чем у автомата Мили, решающего ту же задачу.

Описание переходов между состояниями для автоматов удобно выражать в виде диаграмм, выполненных в виде графов. Если состояния имеют единственную последовательность переключений, то такой автомат называется детерминированным. Если из одного состояния возможно выполнить несколько переходов, то автомат называется недетерменированным.
Цифровой автомат также может однозначно описываться таблицей переходов и таблицей выходов, которые связывают состояния ячеек памяти и входных сигналов. В каждой ячейке таблицы переходов размещаются следующие значения памяти, которые получаются под воздействием входного сигнала при текущем состоянии.
❯ Машина Тьюринга
И вот, наконец вычислительная техника вплотную приблизилась к появлению компьютеров, для которых уже недостаточно было только разработать схему, но и требовалось разработать программное обеспечение. Естественно, что это потребовало новых математических теорий.
Машина Тьюринга была предложена для формализации понятия алгоритма, и является расширением или частным случаем конечного автомата. Сам Алан Тьюринг использовал понятие «вычислительная машина» («computing machine»).

Отдельно останавливаться на самом Тьюринге нет смысла, личность его достаточно известна. Чего стоит только один фильм "Игра в имитацию" с великолепным Бенедиктом Камбербэдчем. Кто не смотрел — крайне рекомендую.
Машина Тьюринга разрабатывалась для того, чтобы ответить на вопрос: «есть ли конкретный метод или механический процесс, который можно применить к математическому утверждению и он ответит, доказуемо ли это утверждение» — которым задавался известный математик Макс Ньюман на своих лекциях в Кембридже.
Нужно понимать, что математикам для работы совершенно не требовалось физически строить машину Тьюринга, а было достаточно ее формализованного описания. То есть машина существует как список правил, по которым она могла бы работать.
Кроме машины Тьюринга появлялись и другие аналогичные теории. К примеру, всего на три месяца позже независимо от машины Тьюринга вышла публикация о машине Поста. Работа над ней велась независимо. Машина Поста также используется в научных трудах благодаря ее простоте.

Гениальность машины Тьюринга заключается в простой идее, что на одной и той же вычислительной машине можно реализовать совершенно разные устройства. Во многом благодаря ей в математике зародилась теория сложности вычислений.
В интернете вы можете встретить достаточное количество программных реализаций машины Тьюринга. Но, на мой взгляд, это не имеет большого прикладного смысла. К счастью, на сегодняшний день существуют другие более эффективные программные решения.
❯ Конечные автоматы в программировании
И так, мы уже увидели, как конечные автоматы используются в математике и электронике. Третье направление, где используется теория конечных автоматов — это программирование. Но не нужно думать, что используется оно в чистом виде.

Идея рассматривать программу в терминах конечного автомата сама по себе не новая. Но наиболее активно свое развитие она получила в начале 90-х годов прошлого века. Одним из основоположников данной идеи является профессор Университета ИТМО Анатолий Абрамович Шалыто. Идея заключается в том, чтобы программировать с использованием понятия «состояние». Сперва для названия этого подхода появился термин "Switch-технологии", так как операторы множественного выбора в традиционных языках подходили для смены состояний программы больше всего. Позже, в конце 90-х термин "Switch-технологии" был заменен на "автоматное программирование".
Теория автоматного программирования — это, прежде всего, отдельное направление в программировании, которое заимствовало некоторые термины и определения из теории автоматического управления, но при этом строится как самостоятельная теория. Для реализации автоматных программ можно использовать диаграммы Мура и таблицы состояний, но сама реализация конечного автомата в автоматном программировании будет отличаться от схемотехнической.
Автоматное программирование можно рассматривать как самостоятельную парадигму. Есть мнение, что оно должно исправить недостатки ООП, и может использоваться как дополнение к нему.
Но, так как специализированные языки для автоматного программирования еще не получили такого распространения, как традиционные языки, точно отделить автоматные программы от программ, написанных более традиционными способами, достаточно сложно. На эту тему идут постоянные споры.
Хочу заметить, что в англоязычном интернете упоминаний о работе Шалыто я не нашел. А Finite State Machine рассматривается как модель для разработки и электрических схем и программных алгоритмов. Каких-то отдельных названий для программирования конечных автоматов я тоже не встречал, обычно так и пишут: "программирование конечного автомата". Хотя, мне лично такое название, как "автоматное программирование", кажется удобным для обращения. На Хабре есть интересная статья, посвященная работе Анатолия Абрамовича, советую почитать.
Но, несмотря на всю неоднозначность, все же рекомендую ознакомиться с работами Шалыто, в частности с его книгой "Автоматное программирование". В ней содержится много полезных прикладных решений. Еще есть сайт автора на эту тему.
Программирование в стиле конечных автоматов получило широкое распространение в системах автоматизированного управления, разработке компьютерных игр, текстовых интерпретаторах, все чаще используется в веб-программировании. Написано большое количество готовых библиотек, реализующих конечные автоматы, на разных языках и для разных систем программирования.
Хорошим примером языка программирования, специализированного на автоматном стиле, является язык последовательных функциональных схем SFC (Sequential Function Chart).
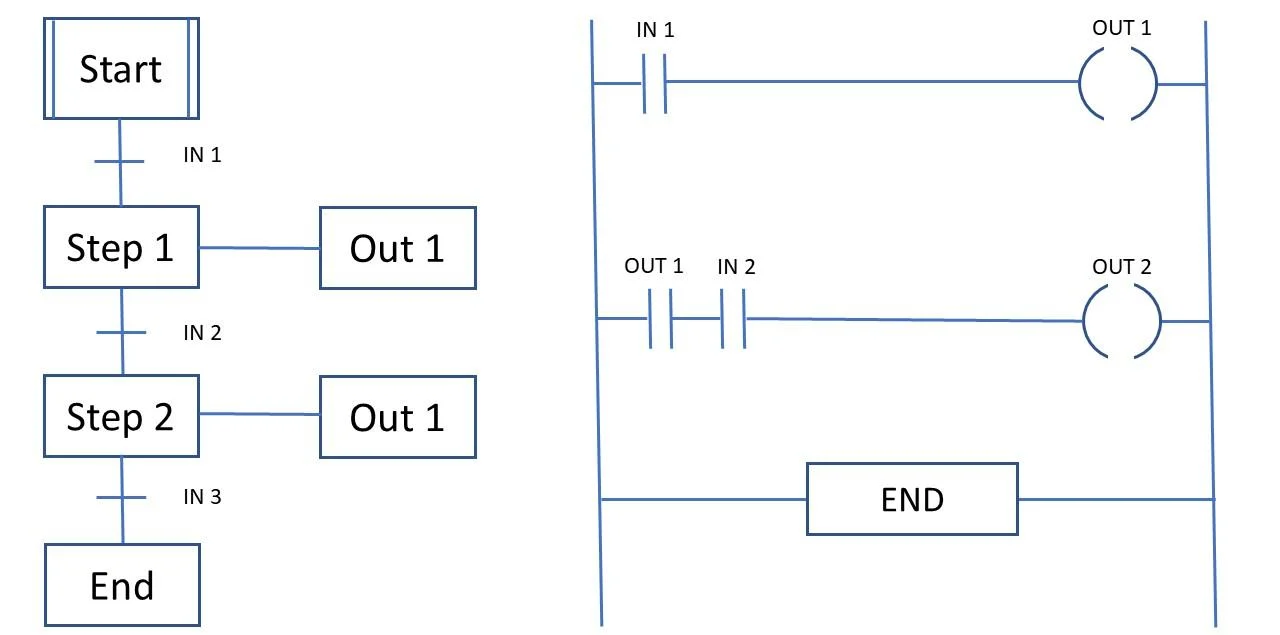
SFC — язык программирования стандарта IEC61131-3, предназначенный для программирования промышленных контроллеров. Широко используется в SCADA/HMI пакетах для программирования промышленных логических контроллеров PLC. Является графическим языком, программа описывается в виде схематической последовательности шагов, объединенных переходами, подобно диаграмме состояний.
Стоит отметить, что подходы, используемые автоматным программированием, очень удобны в разработке программ для микроконтроллеров.
❯ Заключение
И все-таки, почему же с конечными автоматами получается такая каша? Мне кажется, что это связано с большим объемом знаний по данной тематике. Не все они имеют прямое отношение к программированию. Да и такая высокая формализация в программировании, как в синтезе электрических схем, скорее всего не нужна. Или все-таки нужна, но программисты обычно не уделяют этому вопросу достаточного внимания?

В общем, можно говорить о том, что такие понятия как: конечный автомат или конечный автомат состояний, и машина состояний или State Mashine, или Finite State Machine (FSM)- являются синонимами. Это связанно с особенностями терминологии на русском и английском языках.
Надеюсь, что дальнейшее изучение теории цифровых автоматов станет для вас значительно проще.

Комментарии (26)

DustCn
00.00.0000 00:00+9Вся статья в одном абзаце:
В ряде случаев в формировании выходного сигнала может задействоваться не только ячейка памяти, но и входной сигнал. Это позволяет сократить количество необходимых состояний. Такая схема называется автомат Мили.
Остальное - вода.
OldFashionedEngineer Автор
00.00.0000 00:00+1Количество "воды" в тексте скорее всего определяется Вашим уровнем погружения в проблематику, для Вас это все и так понятно и не имеет важного значения.
Я упоминал о проблемах "жонглирования" терминологией, это часто встречается в публицистических материалах, где авторы придерживаются аналогичной точки зрения. Это вызывает достаточно проблем у тех, кто начинает разбираться в материале самостоятельно.
Я просматривал большое количество статей по программированию ардуино. Там часто встречаются разные интерпретации терминов конечных автоматов. К примеру, встречаются абревиатуры FSM в названиях функций. И часто ни каких пояснений на этот счет не дается.
А связь между автоматом Мура и машиной Тьюринга? Это тоже кажется очевидным только для человека, который уже какое-то время связан с темой.
Я не оправдываюсь. Цель статьи была в том, чтобы сфокусировать внимание на базовых терминах и их связи друг с другом. И то, что Вы считаете "водой", является необходимой текстовой оберткой для этих терминов, чтобы сформировать определенное отношение к информации у читателя.

atd
00.00.0000 00:00+1о проблемах "жонглирования" терминологией
Да, действительно такая проблема есть. Причём я не подозревал о её существовании, пока сам не начал писать статью свою на хабр и хотел дать какие-то приличные сслыки, но нет, интернет захламлён текстами разного уовня сомнительности по этой теме :(

OldFashionedEngineer Автор
00.00.0000 00:00+1Вооот! И я столкнулся с этой проблемой. Начал писать статью про конкретную схему, а получился разбор понятий. Разбор схемы просто сюда не влез. Тема сложная, очень много теории, примеры в интернете очень обстрактные.

Indemsys
00.00.0000 00:00+4По ходу сами немного запутали тему. На рисунке про SFC показали Ladder диаграмму.
А Ladder диаграммы не демонстрируют состояний, это не есть изображение автоматов.Сами SFC тоже только узкое подмножество реализаций автоматов.
Чистые автоматы Мура также не очень-то годятся для программирования из-за своей выразительной ограниченности и плохой масштабируемости.
На западе икона автоматного программирования - Miro Samek
Он сразу смекнул, что просто автоматных диаграмм недостаточно для облегчения программирования и сразу начал с UML и фреймворка под автоматы. Теперь там целая экосистема с тулсами, генераторами кода, отладчиками и проч.
Но это как бы бюджетный вариант.Серьёзный вариант - это автоматные среды в Matlab (StateFlow) или LabVIEW (Statechart Module). И там будут не голые автоматы Мура, а комплексные проприетарные графические объекты, лишь частично подражающие автоматам, но они при этом гораздо выразительнее и читабельнее.

Pyhesty
00.00.0000 00:00Спасибо за ссылки!
"Теперь там целая экосистема с тулсами, генераторами кода, отладчиками и проч. " посмотрел обучающее видео, где предлагается помигать светодиодом, выглядит настолько страшно, что новичкам точно не зайдет... удивительно, но примеры выглядят сложнее, чем могли бы быть (имхо)

видимо типичный кодинг конечных автоматов.... 
Indemsys
00.00.0000 00:00Тексты автоматных программ не принято смотреть. Они синтезируются компиляторами из графической нотации. Вот графическую нотацию и представляют на обозрение.
Сам я с quantum leaps давно дел не имею. Их графическая нотация и возможности по кодогенерации и отладке слишком ограничены. Но там хорошо показана внутренняя кухня. Это хорошая альтернативна сбивчивым и путанным статьям по автоматному программированию.
Кстати да, отбивает охоту напрямую писать тексты в автоматном стиле. Этот метод давно устарел.
Pyhesty
00.00.0000 00:00а как корректно реализовать работу с периферией: SPI, I2C, UART, АЦП, протоколы верхнего уровня? если нужных протоколов нет в базе или нужно самому описать (например, сохранение данных в ПЗУ? проприетарный протокол). Если нужно ногой подергать или данные вывода получить, или на экран вывести и библиотеки все есть, то понятно, а если библиотек под нужный процессор нет?
ps: ещё такой момент, кто отвечает за сброс автомата, чтобы он не завис в каком-то состоянии?

Indemsys
00.00.0000 00:00Вы как будто задаете вопрос в парадигме автора, который считает что теория автоматов как-то помогает в программировании. Это все равно что теория матриц помогала бы в схемотехнике. Однако математики не сильны в схемотехнике.
Я же считаю что автоматное программирование это прежде всего графическая нотация с явно изображенными состояниями. И главное преимущество в том что такая нотация избавляет от бесчисленных именований и облегчает глобальный рефакторинг алгоритмов и систем.Но у этой нотации есть свои накладные. В частности при работе с периферией нужна постоянная работа и исследования на уровне символьной отладки и манипуляции с битами на уровне машинных кодов. Здесь сорсы сгенерированные из диаграмм состояний неудобны и процесс неоправданно затягивается..
Поэтому я не применяю метод диаграмм состояний для разработки драйверов. Автоматное программирование хорошо ложиться на сложные многосоставные системы где рефакторить приходится уже на уровне архитектуры приложения верхнего уровня.
Также не применяю автоматы для создания библиотек. Поскольку библиотеки обязаны иметь API. А реализовывать API в диаграммах состояний в графической нотации это удовольствие крайне сомнительное.
Чтобы автомат не зависал в него вставляют автоматы реализующие таймауты.

khe404
00.00.0000 00:00+1Как то у меня эта статья ассоциируется со школьной программой по информатике 30 летней давности. Когда классе в 7м начинается изучение двоичной системы исчисления, но до 11 класса остается совершенно непонятным зачем эта двоичная система исчисления была нужна и как она вообще связана с информатикой.
Это происходит потому, что в школьной программе был совершенно упущен пласт информации который позволял бы понять что вообще такое компьютер.
И из 2й системы исчисления школьники прыгали сразу в паскаль, где двоичная система нужна была разве чтобы сложные конструкции с if писать.
Так и в статье перечисляется набор фактов о развитии информатики и конечных автоматов, перечислены основные элементы, но вот как это работает непонятно.
Вроде как можно разобраться что простейший дверной замок это некий конечный детерминированный автомат Мура. (Есть два состояния. Некий сигнал-ключ может менять состояния.) А если замок устроен так, что правильный ключ нужен для того чтобы открытую дверь еще и распахнуть, то это уже ближе к автомату Мили.
А дальше разрозненные факты про машину Тьюринга и отсылка к тому что это разновидность автомата. И далее высокоуровневые автоматные языки программирования.
На самом деле любой компьютер это конечный автомат с колоссальным количеством состояний и алгоритмами перехода между состояниями зашитыми в процессор. ( Состояние это прям все отдельные биты любой памяти компьютера включая регистры). А ключом к пониманию автоматов является как раз осознание полноты и избыточности системы алгоритмов перехода между состояниями, адресации, разделения памяти на команды и данные и многое что еще.
Сами переходы между состояниями в любом компьютере осуществляются с использованием машинных кодов, которые, с момента включения питания компьютера выстраиваются в непрерывную цепь команд приводящих к изменениям состояний и в конечном итоге складываются в последовательность бит на экране компьютера подсвечивающих пиксели разных цветов.
Зачем нужно разбираться в классификации конечных автоматов, если только вы не разрабатываете свой процессор? В общем как и в любой огромной теме любое обсуждение рождает больше вопросов чем дает ответов и нужно множество примеров.

OldFashionedEngineer Автор
00.00.0000 00:00У меня не было цели разбираться в классификации. Посмотрите вебинар от яндекса, ссылка в начале есть. В терминах путаница полнейшая. А потом получается, что что-то полезное в теории фиг найдешь. В сети встречал доклад от программиста с яндекса, он рассказывал как использовать библиотеку автоматов для мобильных игр под IOS для приложений. И еще куча подобного есть.

khe404
00.00.0000 00:00+2Я прекратил слушать указанный вебинар Яндекс уже на первых минутах, когда лекторы не смогли внятно определить то о чем они собираются рассказывать. Стало ясно что их описание будет основано на процессе классификации банковских карт. (Что пожалуй не самое характерное применение). Мне кажется, что вы начали с очень верных вещей а именно связи формальной логики, математики, устройства памяти, а затем замяли основную канву и очень поверхностно описали задачи которые решают машины состояний и процесс их работы. Хотя базу подготовили прям очень хорошую.

OldFashionedEngineer Автор
00.00.0000 00:00Спасибо, Вы верно меня поняли. Хотелочь буквально на пальцах обьяснить, в каком порядке все это связано. Планирую продолжить тему с прикладными примерами.

OldFashionedEngineer Автор
00.00.0000 00:00За последнее время мне на доработку попадает уже второй проект на микроконтроллере. В последнем программа написана в около автоматном стиле. Вроде человек старательно писал. Но такого нагородил, что в конце уже как-то внятно дополнить функциональность невозможно. Программированием микроконтроллеров часто занимаются электронщики, которые программирование самостоятельно доучивали. Из-за недостатка теоретической базы такой трешак накручивают в программах.

khe404
00.00.0000 00:00Ну, кмк этому в институтах не учат. Скорее просто общей философии программирования. Хотя, довольно давно сталкивался с описанием "C" функции int atoi(char**) в разрезе машины состояний и это было пожалуй очень вдохновляюще. Весь бардак из вложенных условий и циклов рассыпался на переходы между состояниями и это позволило автору описать сложный механизм очень просто. Даже самому тогда захотелось попробовать написать реализацию. Жаль только статья потерялась за давностью лет. Признаться и сегодня хотел увидеть нечто подобное.

Pyhesty
00.00.0000 00:00+1угу (вздыхая), а потом когда берешь в руки клавиатуру, все кажется автоматами с конечным (но это не точно) количеством состояний... знаем... проходили...
и кодишь автомат... просто потому, что так надежнее...
кто как в итоге кодит микроконтроллеры?

OldFashionedEngineer Автор
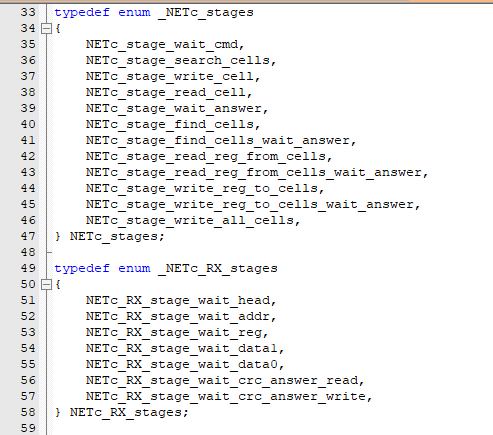
00.00.0000 00:00Автоматы стоит разобрать, чтобы, к примеру, документировать код. Диаграмм Мили - удобный инструмент.

OldFashionedEngineer Автор
00.00.0000 00:00Я имя типа и имя перечисления делаю одинаковыми, подчеркиваеие можно не ставить. В конце перечисления ставлю имя типа максимальное_состояние. С его помощью можно размеры массивов определять и прочее подобное.

imdragon
00.00.0000 00:00+1Упомянутый выше " экосистема с тулсами, генераторами кода, отладчиками и проч. " очень помогает разработать архитектуру решения для микроконтроллера. Это вариант реализации концепции Visual Thinking с разными причудами. Тот же microsoft предлагает использовать FSM для написания UI под частные решения с микроконтроллерами. Я это использовал для проекта с stm32f4. С определенными ограничениями мне это понравилось.
А вообще, когда надо делать что-то серьезное с "0", то проект стоит начинать дизайнить в чем-то большом и развитом. Я люблю Sybase Power Designer. Только вот с FSM в нём трудно.

MasterMentor
00.00.0000 00:00Как корабль назовёшь, так он и поплывёт: "С чем едят конечный автомат". В статье рассмотрели "конечный автомат" и даже их сорта не давая определения конечного автомата. Пичалька. Википедия на порядок информативней. https://ru.wikipedia.org/wiki/Конечный_автомат

OldFashionedEngineer Автор
00.00.0000 00:00-2Абстрактный автомат — это математическая абстрактная модель дискретного устройства, имеющего один вход и один выход, в каждый момент находится в одном состоянии из множества вовозможных.т
Определение в статье есть.

Indemsys
00.00.0000 00:00+1Хорошая цитата от туда -
Кроме того, попытка разработки сложной модели, реализованной конечным детерминированным автоматом, приводит к быстрому росту числа состояний автомата, что в итоге делает разработку такой модели крайне трудоёмкой. Как было отмечено выше, последнюю проблему можно решить, если использовать недетерминированный автомат.
Я бы добавил , что проблему решают иерархические автоматы и параллельные автоматы с механизмами событий.
Но это уже будут совершенно не автоматы Мура, а диаграммы состояний.
Вот тут главная путаница и состоит. Большинство за автоматы принимает или выдаёт обработчики иерархических состояний. Поскольку в чистых автоматах Мура программировать практически невозможно.
OldFashionedEngineer Автор
00.00.0000 00:00-1Не бывает универсальных инструментов. Так и автомат Мура можно реализовать на Си, только для ограниченного круга задач

Indemsys
00.00.0000 00:00Речь просто о том что автоматы - это не инструмент. Это метод в некоей среде разработки. И без указания среды ценность этого метода оценить невозможно.




iskateli
не рассмотрены такие типы как:
- Вероятностный автомат
- Квантовый автомат
- Машина вероятности (Различные варианты понятия «Машины вероятности» являются обобщениями понятий «автомата детерминированного», «Тьюринга машина», «автомата бесконечного».)
не рассмотрено разделение по следующим типам:
- автоматы-распознаватели
- автоматы-преобразователи
- автоматы-генераторы
OldFashionedEngineer Автор
Основная цель, заявленная в статье, разобраться в базовых терминах и не запутать читателя еще больше.
Об этом хочется написать с практическими примерами. Теории в статье хватает.