Рассмотрение задачи анализа структуры разнообразных сетей равно, как и структуры многих других систем, формирование показателей свойств структур приводит к необходимости анализа системных элементов, связей и их взаимного размещения. Чаще всего структура системы моделируется графом поэтому важной составной частью такого анализа является задача о путях в графе.

Большой теоретический и практический интерес представляет не только решение задачи существования, в которой отыскивается ответ на вопрос о наличии путей между какими-то узлами структуры, о числе таких путей, но и решение задачи о перечислении самих этих путей. В литературе [1-12  ] методам решения этих задач уделяется достаточно много внимания, что говорит об их значимости, приводятся алгоритмы получения решения, но к сожалению часто не приводятся данные по оценкам самих алгоритмов. В предлагаемой автором работе рассматривается оригинальный подход к перечисления всех путей в графе между парой фиксированных вершин. Алгоритм является базовым для решения многих других задач (некоторые предполагается рассмотреть в последующих публикациях) и обладает хорошими вычислительными характеристиками.

Основные положения

 В нашей задаче перечисления всех путей мы будем использовать два замечательных принципа: первый принцип – разворачивания графа в многоярусное дерево путей и второй принцип – представление отдельного пути числом позиционной системы счисления со специальным основанием.  Первый принцип обеспечивает точность перечисления (без пропусков путей), а второй – обеспечивает упорядочение множества всех путей по значению числового эквивалента пути.

Исходные данные

 Задание исходных данных в разных задачах может сильно различаться.  Не всегда следует стремиться к простой форме задания исходных данных. В ряде случаев предварительная подготовка исходных данных позволяет упростить схему алгоритма получить выигрыш при уменьшении сложности алгоритма и программы.

Тщательная проработка и подготовка исходных данных часто обеспечивает построение более простых алгоритмических решений, так как когнитивные способности человека легко устанавливают упорядочение элементов в множествах и подмножествах, а для алгоритма и программы это может быть и не сложно, но требует времени на анализ ситуации и занимает ресурсы. В предлагаемой публикации как раз предоставляется такой случай.

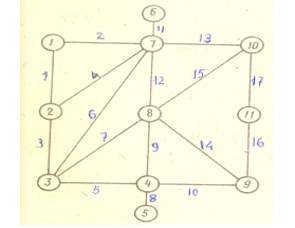
Когда граф перед глазами, мы без труда видим число вершин и ребер, степени вершин, смежные вершины и другие особенности структуры графа.

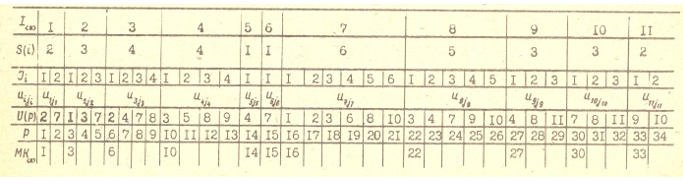
Для задачи перечисления путей между парой вершин (А=2 и В=10) задание графа в памяти ПК осуществляется путем формирования таблицы 1; в качестве исходных данных массивов и переменных (табл. 1) используются:

• массив I_<N> номеров вершин I_<N> = <1, 2, 3, ..., N>; i =1(1)N, N – размерность массивов, первая строка таблицы; вторая строка – полустепени захода вершин графа; в третьей строке перечисляются порядковые номера вершин смежных с текущей вершиной; четвертая строка содержит обозначения подмножеств номеров смежных вершин в графе, а в пятой строке содержатся сами графовые номера вершин, смежные с текущей;

• массив полустепеней выхода S⁺(i) вершин, упорядоченных по возрастанию номеров вершин графа S_<N>= <S⁺(1), S⁺(2), …, S⁺(i), …, S⁺(N)>, где i – текущий номер вершины;

• массив {Uij_i}= <uij₁, uij₂, uij₃, …, uij_S(i)> номеров вершин, упорядоченных по возрастанию значений номеров вершин графа, смежных с вершиной v_i, и в каждую из которых проведена дуга из вершины v_i;

• массив, содержащий упорядоченные по возрастанию номеров вершин графа подмножества U(P)=u(ij_i) =<{uij₁}, {uij₂}, …, {uij_i}, …, {uij_N}>; i = 1(1) N, j_i = 1(1) S⁺(i); р – текущий номер элемента массива U(P);

• массив МК_<N>, содержащий значения индекса р номеров вершин ui₁ ϵ {uij_i}, i =1(1)N.

Дерево путей графа

Определение. Маршрутом в графе G называется чередующаяся последовательность вершин и ребер v_о, р₁, v₁, …, v_n-1, р_n, v_n; она начинается и заканчивается вершиной, каждое ребро (дуга) последовательности инцидентно двум вершинам (до и после ребра). Такой маршрут соединяет пару вершин v_о, v_nи его можно обозначать более кратко через номера вершин v_о v₁ v₂…v_n; маршрут замкнут, если v_о= v_n; маршрут называется цепью при различных ребрах и простой цепью при различных вершинах; замкнутая цепь называется циклом.

Определение. Граф называется ациклическим, если в нем нет циклов.

Определение. Дерево – это связный ациклический граф. В основе алгоритма решения задачи о перечислении путей в графе лежит метод формирования дерева путей, связывающих некоторую вершину (А) со всеми другими, и последовательного обхода его ветвей с целью поиска фиксированной конечной (В) вершины пути. При поиске вершины В алгоритм выполняется обходом по ветвям дерева всех вершин, лежащих на ярусах дерева, которые отстоят от корня (вершины А) не более чем на W ярусов.

Если граф имеет большую размерность, то часть путей может оказаться непомерной длины. Тогда можно ограничиться поиском путей между А и В с длиной, не превышающей W.

Определение. Ярусом дерева называется множество вершин, которые на дереве путей связаны с корнем одинаковым числом дуг.

Перечисление (формирование) путей в графе

В целях удобства обработки результатов перечисления предусмотрена возможность ограничения длины перечисляемых путей, вводится характеристика длины пути (W), ее значение задается количеством вершин, которое не должно быть превышено ни в одном из перечисляемых путей. При снятии ограничения на длину пути алгоритм перечисляет все простые пути из А в В.

Формирование отдельного пути

В основной памяти заготавливается массив Т (w), в котором будут формироваться последовательно все пути. Ячейки этого массива будем называть элементами пути и обозначать символом Т (ks), где ks – текущий номер элемента пути (ячейки массива Т (w), ks = 1(1)W). Каждый путь на графе (орграфе) формально описывается размещенной в массиве Т (w) последовательностью номеров вершин графа, через которые он проходит.

Основная идея алгоритма формирования отдельного пути состоит в том, что в массив Т(w) последовательно заносятся номера соответствующих вершин графа до тех пор, пока в нем очередным номером вносимой вершины не окажется номер (В) конечной вершины формируемого пути.

Эта последовательность номеров рассматривается как некоторое w – разрядное число N-ичной позиционной системы счисления, 2 ≤ w ≤ N. Число (путь) формируется следующим образом. Номер вершины (А) первой в формируемом пути записывается в старший (левый) разряд (ячейку массива Т (ks = 1)) числа. Номер вершины второй в пути записывается в соседний справа разряд (Т (ks = 2)), меньший по старшинству, и так далее, пока не встретится конечная вершина (В) пути или последующий выбор вершины станет невозможным.

Номер вершины (В) записывается в младший разряд, соседний с заполненными разрядами. Незаполненные разряды в массиве Т (w), если такие имеются считаются нулевыми. Каждому пути в графе соответствует некоторый числовой эквивалент. Таким образом, в основной памяти создается массив Т (w) первого пути, где будут последовательно формироваться все другие пути между парой фиксированных вершин А и В.

Формирование последовательности путей из фиксированной вершины

Содержимое промежуточных (между А и В) элементов пути (номеров вершин графа) частично или полностью изменяются при переходе от одного пути к другому. Очевидно, что крайние элементы пути не изменяются и содержат во всех случаях номера вершин А и В соответственно.

Формирование последовательности путей определяется следующим правилом. Если каждый путь, состоящий из цифр-номеров вершин, рассматривать как некоторое число позиционной системы счисления, то последовательность путей должна формироваться в таком порядке, который обеспечивает монотонное возрастание значений числового эквивалента на последовательно перечисляемых путях между парой фиксированных вершин А и В. Многозначные числа (десять и более) считаются размещенными в одном разряде (элементе Т (w)).

Сформулированное правило обеспечивается алгоритмически выбором очередной вершины для включения в формируемый путь и выполнения при таком выборе ряда условий:

а) каждый путь должен отличаться от предшествующего хотя бы одной промежуточной вершиной, номер которой должен быть больше номера вершины в предшествующем элементе Т (ks) предыдущего пути, для которого происходит замена содержимого ячейки. При этом числовой эквивалент пути должен монотонно возрастать;

б) ни одна вершина не должна встречаться в пути более одного раза, путь не должен содержать циклов (контуров);

в) очередной путь должен формироваться на основе предыдущего посредством изменения содержимого хотя бы одного элемента Т(ks) предыдущего пути, начиная от конечной вершины и в соответствии с условиями «а» и «б»;

г) если в каком-то элементе предыдущего пути находилась вершина vij ϵ{uij_i} с меньшим номером, то в формируемом новом пути она должна быть заменена вершиной vij₁+1ϵ{uij_i} с большим номером, взятой из этого же подмножества, если оно не исчерпано;

Структурная схема программы

 Логические зависимости и связи переменных становятся более прозрачными и понятными, когда они прописываются явно и комментируются в рамках структурно-логической схемы. Аналогично и представление функций, выполняемых отдельными операторами и процедурами, сопровождаемые пояснениями.

Переменные и обозначения

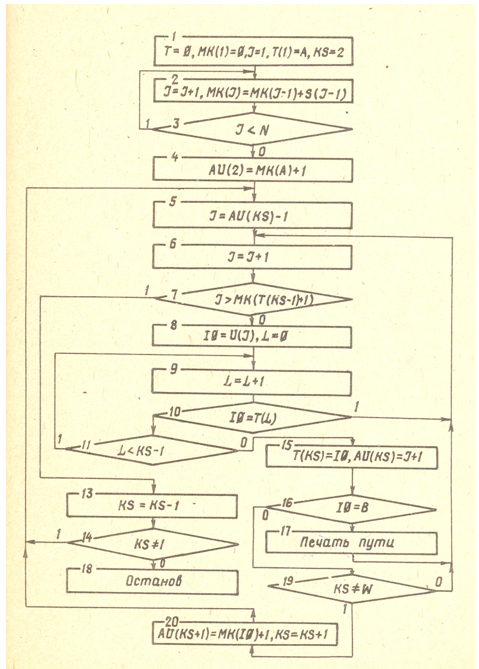
 Поясним подробно работу алгоритма (программы по схеме рис.3). Используются следующие объекты и их обозначения:

А, В – имена (номера) вершин, между которыми программой перечисляются все простые пути не длиннее w =7; А – начальная вершина; В – конечная вершина пути;

S_<N> = S(N) – массив полустепеней выхода вершин графа;

S(i) – текущий элемент массива S(N);

i –текущий номер (индекс) элемента массива S_<N>,  i =1(1)N;

N –размерность массива вершин графа, равная числу вершин;

U(p) = U_<p> – массив связей графа; u(p) –текущий элемент массива U_<p>;

р – текущий номер (индекс) элемента массива U_<p>, р =1(1)Р;

Р – размерность массива связей графа, равная числу связей Р = 2k +L;

k –число ребер; L – число дуг в графе;

Т_{< w >} = T(w) – массив элементов пути;

Т(ks) – текущий элемент пути; ks – текущий номер элемента пути;

W – максимальное число вершин, которое может быть по желанию пользователя включено в путь, W = 2(1)N; N – наибольшее число вершин, образующих путь;

МК_<N+1> = MK(N+1) – массив индексов р, указывающих на те элементы массива U(p), которые являются первыми (ui₁) в массивах{uij_i} смежных вершин;

MK(i) +1 – значение индекса р, соответствующее вершине графа с номером i;

i –текущий номер (индекс) вершины графа;

AU_<W–1> – вспомогательный массив индексов р, указывающих при рассмотрении очередной позиции-вершины uij ϵ{uij_i}в качестве кандидата для включения в элемент пути Т(ks), на вершину uiℓ₊₁ ϵ{uij_i}, т.е. на следующую в массиве U(p) за рассматриваемой. Индекс i определяется однозначно, он равен номеру вершины, находящейся в элементе пути Т(ks –1), т.е. в предыдущем элементе пути. При непригодности вершины uiℓ следующий кандидат будет взят из U(AU(ks)).

AU(ks) – текущий элемент массива AU_<W–1>.

L – вспомогательная переменная, параметр цикла.

 Действия алгоритма, реализуемые в соответствии со схемой

 В первом блоке (см. схему алгоритма) осуществляется подготовка данных и программы для исполнения. Объявляются переменные и массивы. Вводятся следующие исходные данные: N, W, A, B, p, s(N), U(p). Состав и порядок следования элементов массивов S(N), U(p) описан ранее, а значения определяются конкретной задачей. Исходные данные для примера даются в (табл. 1).

В блоке 1 обнуляются элементы массива Т(w), где будут формироваться перечисляемые пути. Первому элементу пути присваивается значение А. Первому элементу массива МК(N+1) присваивается значение нуль. Текущему номеру элемента пути (ks) присваивается значение 2, так как первый элемент Т(1) уже содержит вершину А и далее путь будет формироваться со второго элемента.

Подготавливается цикл для формирования массива МК(N+1). Параметру цикла J присваивается значение единица Т= 0, МК(1) =0, J = 1, Т(1) = А, ks = 2.

В блоках два, три организован цикл, формирующий по рекуррентной формуле элементы массива МК(N+1); МК(I) = ∑_i=1S(I), I = 2(1)N+1, I = I+1, MK(I) = MK(I–1) +S(I – 1).

Блок 4 определяет индекс J = p очередного кандидата (вершины графа) из множества {uAj_A} для элемента пути с номером два: AU(2) = MK(A) +1.

В блоках 5 и 6 организуется цикл с параметром (J) для использования вершин множества {uksj_ks} в процессе формирования путей, причем используется сквозной индекс J = p массива U(p), а в множестве {uksj_ks} анализируются при формировании очередного пути не все элементы, а начиная с очередного подходящего, индекс которого предварительно заносится в элемент AU(ks) на предшествующем проходе по циклу. Это позволяет избежать многократного избыточного повторения операций анализа пригодности кандидатов и улучшить характеристику быстродействия алгоритма.

В блоке 7 осуществляется проверка законченности цикла по J и управления его повторением. Если цикл завершен, т.е. J > MK(T(ks – 1)+1), то управление передается в блок 13;

Если цикл не завершен, то управление передается в блок 8.

В блоке 8 обнуляется параметр цикла по L, L = 0 и осуществляется выбор вершины графа из подмножества {ur(ks-1)j_r(ks-1)} в соответствии с условием «а» и имеющей номер J в массиве U(p); эта вершина является кандидатом для внесения в элемент Т(ks) формируемого пути: I0 = U(J).

В блоке 9 организуется счетчик цикла (по L) проверки условия пригодности (допустимости включения в путь) вершины I0: L = L+1, где L – текущий номер элемента сформированной части пути (имеет смысл ks);

В блоке10 проверяется условие «б» правила пригодности испытываемой вершины I0 для включения ее в путь, т.е. проверяется, не встречалась ли вершина I0 в предшествующей части пути.

Если вершина с номером I0 включена ранее в путь, то управление передается в блок 6;

Иначе управление передается в блок 11.

В блоке 11 проверяется условие завершения цикла по L, т.е. проверяется, все ли вершины предшествующей части сформированного пути сравнивались с вершиной I0;

L< ks – 1, где (ks – 1) – длина уже сформированной части пути.

Если все вершины проверены и ни одна из них не совпала с I0, то управление передается в блок 15;

Если не все вершины пути проверены, то управление передается на начало цикла по L блок 9.

В блоке 6 организуется счетчик цикла (по J) последовательной в соответствии с условием «г» выборки из подмножества {ur(ks-1)j_r(ks-1)} вершин-кандидатов I0 в элемент Т(ks) формируемого пути: J = J+ 1. Управление из этого блока передается в блок 7.

 З а м е ч а н и е. Управление последовательным выбором вершин-кандидатов I0 для включения в элемент Т(ks) пути осуществляется выполнением событий-условий:ℓ

• испытываемая вершина I0 забракована в блоке 10 схемы, управление передается в блок 6, где происходит наращивание индекса J и затем в блок 7;

• испытываемая вершина I0 не забракована в блоке 10 схемы, но оказалась конечной вершиной, т.е. (I0 = В) пути. В этом случае после печати пути (блок 17) управление передается в блок 6;

• испытываемая вершина I0 не забракована в блоке 10 схемы, но вносится в последний элемент пути Т(W), т.е. ks = W. Дальнейшее формирование пути наращиванием его элементов прекращается. В подмножестве {u(T(ks –1)j_{T(ks –1)})} подряд просматриваются (обрабатываются) все вершины и отыскивается (при наличии в этом подмножестве) конечная вершина (В) пути. Управление передается в блок 6.

В блоке 13 осуществляется (при условии окончания обработки вершин очередного подмножества) {u(T(ks –1)j_{T(ks –1)})} и невозможности наращивания) укорочения длины пути, т.е. ks = ks–1, управление передается в блок 14, где проверяется условие исчерпания всех путей между А и В в заданном графе: ks ≠ 1.

Если все пути исчерпаны (напечатаны), т.е. условие выполняется, то управление передается для завершения задачи в блок 18 «Останов». Если множество путей еще не исчерпано, то управление передается в блок 5.

В блоке 15 вершина, которая удовлетворяет условию блока 10, т.е. не встречалась ранее в строящемся пути, вносится в элемент Т(ks) пути: Т(ks) = I0.

Для исключения просмотра уже обработанных вершин подмножества {U(T(ks –1)j_{T(ks –1)})} в соответствии с условием « г », сформулированным ранее, при следующих проходах в ячейке AU(ks) массива AU_<W–1> запоминается индекс очередной необработанной еще вершины этого подмножества: AU(ks) =J +1. После этого управление передается блоку 16. В этом блоке проверяется условие, является ли выбранная вершина I0, внесенная в блоке 15 в элемент Т(ks) = I0 пути, конечной вершиной пути: I0=В?

Если I0 является конечной вершиной пути, то формирование очередного пути завершено и управление передается в блок 17.

Если I0 не является конечной вершиной пути, то управление передается в блок 19.

В блоке 17 полученный в массиве Т(W) путь печатается принтером.

Очевидно, что формирование следующего пути из построенного наращиванием длины исключено, так как путь уже содержит конечную вершину (В). Следовательно, формирование следующего пути допустимо только способом изменения содержимого Т(ks)-го элемента пути, а при невозможности такого изменения осуществляется последовательным изменением предшествующих Т(ks – i), i =1(1)ks–1, элементов или совсем прекращается при полном исчерпании множества всех путей. Управление передается в блок 6.

В блоке 18 выполняется завершение программы и остановка процесса перечисления путей.

В блоке 19 при условии, что вершина I0 не является конечной вершиной пути, проверяется возможность дальнейшего наращивания длины пути, т.е. проверяется условие, является ли элемент Т(ks) последним элементом Т(W) массива: ks ≠ W.

Если условие не выполняется, то управление передается в блок 6, так как наращивание исключено по условию ограниченной длины пути.

Дальнейшее формирование путей возможно только способом изменения содержимого элемента Т(ks = W) при невозможности такого изменения последовательным изменением предшествующих элементов Т(W – i), i =1(1) W –1.

При выполнении условия ks ≠ W управление передается блоку 20, в нем осуществляется наращивание числа элементов формируемого пути, т.е. ks = ks + 1. В этот блок алгоритм приходит в результате совместного выполнения двух событий-условий:

• вершина I0, внесенная в Т(ks)-й элемент пути не является конечной вершиной (I0 ≠ В);

• заполненный элемент пути Т(ks) = I0 не является последним (по длине) элементом пути ks ≠ W.

При этом целью исключения многократного прохождения (формирования заново) имеющейся части пути до элемента Т(ks) включительно наращивание необходимо выполнить выбором очередного ранее обрабатывавшегося элемента массива U(р). С этой целью предварительно определяется индекс очередного элемента массива U(р), который записывается в элемент AU(ks +1) массива AU_<W–1>: AU(ks +1) = MK(I0)+1.

Этот индекс определяет текущий номер J очередной вершины в множестве U(р), с которой и должен продолжаться подбор подходящей вершины в следующий элемент пути. После чего управление передается в блок 5.

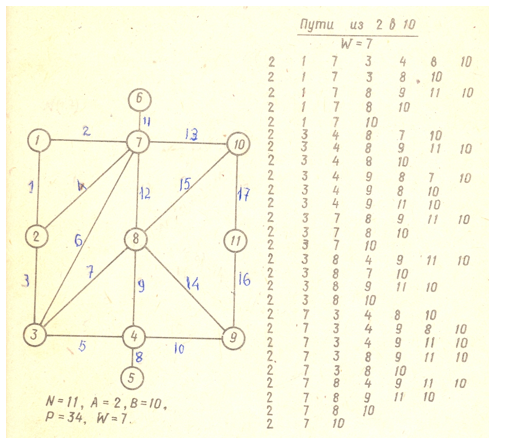
 Пример .  Для заданного графа G (11, 17) с характеристиками N = 11, A = 2, D = 10, p =34, w= 7 перечислить все пути, длина которых не превышает семи вершин. Предполагается, что граф ориентированный и каждое ребро графа представляет пару встречно направленных дуг.

Заключение

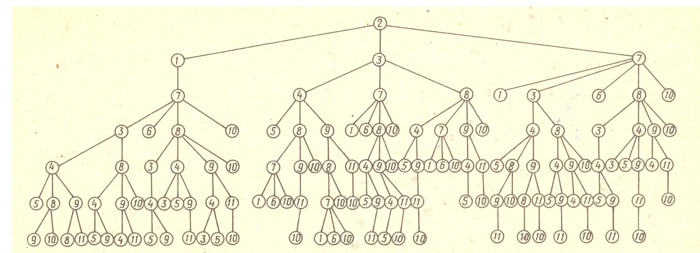
Таким образом, рассмотренный алгоритм обеспечивает перечисление путей в графе  между парой (А и В) фиксированных вершин. Работу алгоритма удобно проследить на графе-дереве путей, построенном для вершины А и связывающего эту вершину А со всеми остальными вершинами. На рис. 4 показан фрагмент множества путей графа, который содержит только семь ярусов (W =7) дерева путей. По этому фрагменту можно легко проследить работу алгоритма, используя числовой пример.