
В 2005 году id Software опубликовала под лицензией GPL-2 исходный код своей игры 1999 года Quake III Arena. В файле code/game/q_math.c есть функция для вычисления обратного квадратного корня числа, которая на первый взгляд выглядит очень любопытным алгоритмом:
float Q_rsqrt( float number )
{
long i;
float x2, y;
const float threehalfs = 1.5F;
x2 = number * 0.5F;
y = number;
i = * ( long * ) &y; // зловещий хакинг чисел с плавающей запятой на уровне битов
i = 0x5f3759df - ( i >> 1 ); // какого чёрта?
y = * ( float * ) &i;
y = y * ( threehalfs - ( x2 * y * y ) ); // первая итерация
// y = y * ( threehalfs - ( x2 * y * y ) ); // вторая итерация, можно удалить
return y;
}Об этом алгоритме написано множество статей, и ему посвящена хорошая страница Википедии, где он назван fast inverse square root (быстрым обратным квадратным корнем). На самом деле, этот алгоритм упоминался на различных форумах ещё до публикации исходного кода Q3. Ryszard из Beyond3D провёл в 2004-2005 годах исследование и в конечном итоге выяснил, что первоначальным автором алгоритма был Грег Уолш из Ardent Computer, который создал его десятью годами ранее.
Как он работает?
Как же работает этот способ? Он выполняется в два этапа:
- получение грубой аппроксимации
yобратного квадратного корня нужного числаnumber:y = number; i = * ( long * ) &y; i = 0x5f3759df - ( i >> 1 ); y = * ( float * ) &i; - Уточнение аппроксимации при помощи одного шага метода Ньютона-Рафсона (NR):
const float threehalfs = 1.5F; x2 = number * 0.5F; y = y * ( threehalfs - ( x2 * y * y ) );
Первая аппроксимация
Самая интересная часть — это первый этап. На нём используется кажущееся «магическим» число
0x5f3759df и битовые сдвиги, что в результате каким-то образом даёт обратный квадратный корень. В первой строке 32-битное число с плавающей запятой y сохраняется как 32-битное целое число i получением указателя на y, преобразованием его в указатель long и разыменованием. То есть y и i содержат два идентичных 32-битных вектора, но один интерпретируется как число с плавающей запятой, а другой — как целое число. Затем целое число смещается на один шаг вправо, меняет знак, и к нему прибавляется константа 0x5f3759df. Наконец, получившееся значение интерпретируется как число с плавающей запятой при помощи разыменования указателя float, указывающего на целочисленное значение i.Здесь сдвиг, смена знака и сложение выполняются во множестве целых чисел, так как же эти операции влияют на число во множестве чисел с плавающей запятой? Чтобы понять, как это может дать нам аппроксимацию обратного квадратного корня, нужно знать, как представлены в памяти числа с плавающей запятой. Число с плавающей запятой состоит из знака
1 Это относится только ко всем обычным числам с плавающей запятой, а ещё существуют два нуля, поднормальные числа и особые значения наподобие
NaN и inf. В алгоритме они не учитываются.В нашем случае можно допустить, что
float имеет формат IEEE 754 binary322, где биты упорядочены следующим образом:2Согласно стандарту C,
float необязательно binary32, но в большинстве архитектур, например, в современных x86, это так. Автор функции Q_rsqrt сделал допущение, что используется binary32.
Самый старший бит — это бит знака
Мы можем написать на C программу
interp.c, которая будет выводить интерпретации заданного числа и в целых числах, и в числах с плавающей запятой, а также выделять разные части:#include <stdlib.h>
#include <stdio.h>
#include <string.h>
#include <stdint.h>
int main(int argc, char *args[]) {
/* парсим число из args */
uint32_t i;
int ret;
if (argc == 2) {
ret = sscanf(args[1], "%u", &i);
} else if (argc == 3 && strcmp(args[1], "-h") == 0) {
ret = sscanf(args[2], "%x", &i);
} else if (argc == 3 && strcmp(args[1], "-f") == 0) {
float y;
ret = sscanf(args[2], "%f", &y);
i = *(uint32_t*)&y;
} else {
return EXIT_FAILURE;
}
if (ret != 1) return EXIT_FAILURE;
/* выводим представления */
printf("hexadecimal: %x\n", i);
printf("unsigned int: %u\n", i);
printf("signed int: %d\n", i);
printf("floating-point: %f\n", *(float*)&i);
/* выводим компоненты */
int S = i >> 31;
int E = (i >> 23) & ((1 << 8)-1);
int e = E - 127;
int F = i & ((1 << 23)-1);
float f = (float)F / (1 << 23);
printf("S: %d\n", S);
printf("E: %d (0x%x) <=> e: %d\n", E, E, e);
printf("F: %d (0x%x) <=> f: %f\n", F, F, f);
return EXIT_SUCCESS;
}Для примера можно рассмотреть число
0x40b00000:$ ./interp -h 40b00000
hexadecimal: 40b00000
unsigned int: 1085276160
signed int: 1085276160
floating-point: 5.500000
S: 0
E: 129 (0x81) <=> e: 2
F: 3145728 (0x300000) <=> f: 0.375000Также можно извлечь части числа с плавающей запятой:
$ ./interp -f -32.1
hexadecimal: c2006666
unsigned int: 3254806118
signed int: -1040161178
floating-point: -32.099998
S: 1
E: 132 (0x84) <=> e: 5
F: 26214 (0x6666) <=> f: 0.003125Но даже теперь, когда мы знаем, как числа с плавающей запятой представлены в памяти, не совсем очевидно, как выполнение операций во множестве целых чисел может повлиять на множество чисел с плавающей запятой. Сначала мы можем попробовать итеративно обойти диапазон чисел с плавающей запятой и посмотреть, какие целые значения получим:
#include <stdio.h>
int main() {
float x;
for (x = 0.1; x <= 8.0; x += 0.1) {
printf("%f\t%d\n", x, *(int*)&x);
}
}Затем можно отметить значения с плавающей запятой на оси X и целые значения на оси Y (например, с помощью gnuplot), чтобы получить следующий график:

Хм, эта кривая выглядит довольно знакомой. Мы можем при помощи нашей программы рассмотреть другие точки данных:
$ ./interp -f 1.0
hexadecimal: 3f800000
unsigned int: 1065353216
signed int: 1065353216
floating-point: 1.000000
S: 0
E: 127 (0x7f) <=> e: 0
F: 0 (0x0) <=> f: 0.000000
$ ./interp -f 2.0
hexadecimal: 40000000
unsigned int: 1073741824
signed int: 1073741824
floating-point: 2.000000
S: 0
E: 128 (0x80) <=> e: 1
F: 0 (0x0) <=> f: 0.000000
$ ./interp -f 3.0
hexadecimal: 40400000
unsigned int: 1077936128
signed int: 1077936128
floating-point: 3.000000
S: 0
E: 128 (0x80) <=> e: 1
F: 4194304 (0x400000) <=> f: 0.500000Для 1.0 и 2.0 мы получаем
127 << 23), а затем сдвинем его до правого края, то получим экспоненту (float) (*(int*)&x - (127 << 23)) / (1 << 23)Тогда мы получим не совсем логарифм, а линейную аппроксимацию всех значений, не являющихся степенью двойки. Мы можем наложить аппроксимацию на реальную логарифмическую функцию:

Это значит, что когда мы возьмём число с плавающей запятой и интерпретируем его как целое, то получим аппроксимацию логарифма этого числа с каким-то смещением и масштабом. А когда мы интерпретируем целое число как число с плавающей запятой, то получаем обратное, то есть показательную функцию или антилогарифм нашего целого значения. По сути, это означает, что когда мы выполняем операции во множестве целых чисел, то это как будто мы выполняем операции в логарифмической области определения. Например, если вспомнить логарифмические тождества, то можно понять, что если взять логарифм двух чисел и сложить их, то мы получим логарифм их произведения:
Иными словами, если мы выполняем сложение во множестве целых чисел, то получаем умножение во множестве чисел с плавающей запятой, только приближенное. Это можно проверить ещё одной простой программой на C. Нам нужно учесть влияние нашей операции на смещение экспоненты. Мы можем сложить два числа со смещёнными экспонентами и получить двойное смещение:
Мы хотим, чтобы смещение оставалось равным
#include <stdio.h>
#include <stdlib.h>
#include <stdint.h>
const uint32_t B = (127 << 23);
int main(int argc, char *args[]) {
/* парсим члены из аргументов args */
float a, b;
if (argc == 3) {
int ret = sscanf(args[1], "%f", &a);
ret += sscanf(args[2], "%f", &b);
if (ret != 2) return EXIT_FAILURE;
} else {
return EXIT_FAILURE;
}
/* выполняем умножение (целочисленное сложение) */
uint32_t sum = *(uint32_t*)&a + *(uint32_t*)&b - B;
float y = *(float*)∑
/* сравниваем с действительным */
float y_actual = a*b;
float rel_err = (y - y_actual) / y_actual;
printf("%f =? %f (%.2f%%)\n", y, y_actual, 100*rel_err);
}Давайте проверим:
$ ./mul 3.14159 8.0
25.132721 =? 25.132721 (0.00%)
$ ./mul 3.14159 0.2389047
0.741016 =? 0.750541 (-1.27%)
$ ./mul -15.0 3.0
-44.000000 =? -45.000000 (-2.22%)
$ ./mul 6.0 3.0
16.000000 =? 18.000000 (-11.11%)
$ ./mul 0.0 10.0
0.000000 =? 0.000000 (inf%)Чаще всего результаты не полностью точны, они точны, только если один из членов — степень двойки, и наименее точны, когда оба члена находятся ровно между двумя степенями двойки.
А как насчёт обратного квадратного корня? Обратный квадратный корень
Это значит, что если мы выполним умножение во множестве целых чисел, то получим возведение в степень во множестве чисел с плавающей запятой. В зависимости от экспоненты
| p | f(x) |
|---|---|
| 2 | |
| 1/2 | |
| -1 | |
| -1/2 |
Чтобы получить первую аппроксимацию обратного квадратного корня, нам просто нужно выполнить умножение на -1/2 во множестве целых чисел и учесть смещение. Тогда смещение будет
- (i << 1) + 0x5f400000;Теперь этот код идентичен исходному коду Q3, только незначительно отличается значение константы. Разработчики Q3 использовали
0x5f3759df, мы пока используем 0x5f400000. Посмотрим, можно ли внести изменения, изучив нашу погрешность. Просто вычтем аппроксимированное значение из точного значения обратного квадратного корня и наложим результат для диапазона чисел на график:
График повторяется по горизонтали в обоих направлениях (только в разном масштабе), поэтому нам нужно только изучить эту часть, чтобы понять погрешность для всех (нормальных) чисел с плавающей запятой. Мы видим, что приблизительное значение всегда даёт слишком высокую оценку; просто вычтя константу, которая примерно вдвое меньше максимальной погрешности, мы можем сделать его симметричным, таким образом уменьшив среднюю абсолютную погрешность. Посмотрев на график, можно понять, что подойдёт вычитание примерно 0x7a120. Тогда наша константа будет равна 0x5f385ee0, что ближе к константе, использованной в Q3. Во множестве целых чисел наша константа просто центрирует погрешность по оси X на показанной выше схеме. Во множестве чисел с плавающей запятой влияние на погрешность будет схожим, за исключением того, что вычитание заимствует из экспоненты:

Потенциально мы могли бы найти реальный оптимум для какой-то разумной функции потерь, но мы остановимся на этом. Не совсем понятно, как была выбрана оригинальная константа Q3, возможно, путём проб и ошибок.
Улучшаем аппроксимацию
Вторая часть более привычна. После получения первой аппроксимации её можно улучшить методом Ньютона-Рафсона (NR). В Википедии есть хорошая статья о нём. Метод NR используется для уточнения аппроксимации корня уравнения.
Так как нам нужен обратный квадратный корень, необходимо воспользоваться уравнением
Если у нас есть приблизительное значение
и именно такое выражение используется во второй части функции в коде Q3.
Насколько он быстр?
В 2003 году Крис Ломонт написал статью о своём исследовании алгоритма. Его тесты показали, что алгоритм был в четыре раза быстрее, чем простое использование
sqrt(x)3 из стандартной библиотеки и получение его обратного значения.3Ломонт написал
(float)(1.0/sqrt(x)), однако sqrt (в отличие от sqrtf) работает с double, а не с float. Вероятно, это могло привести к замедлению наивного метода, потому что могло вызвать преобразование типов из double и обратно.В 2009 году Илан Раскин написал пост Timing Square Root, где он в основном изучал функцию квадратного корня, но также и сравнил алгоритм быстрого обратного квадратного корня с другими методами. На его Intel Core 2 быстрый обратный квадратный корень был в четыре раза медленнее, чем
rsqrtss, или на 30% медленнее, чем rsqrtss с одним шагом NR.С тех пор в наборе команд x86 появилось множество новых расширений. Я попытался найти все имеющиеся сегодня команды, связанные с квадратным корнем:
| Набор | Ширина | ||
|---|---|---|---|
| x87 (1980 год) | fsqrt |
32 | |
| 3DNow! (1998 год) | pfrsqrt |
128 | |
| SSE (1999 год) |
sqrtps, sqrtss
|
rsqrtps, rsqrtss
|
128 |
| SSE2 (2000 год) |
sqrtpd, sqrtsd
|
128 | |
| AVX (2011 год) |
vsqrtps, vsqrtpd, vsqrtps_nr, |
vrsqrtps, vrsqrtps_nr
|
256 |
| AVX-512 (2014 год) |
vrsqrt14pd, vrsqrt14ps, vrsqrt14sd, vrsqrt14ss
|
512 |
Сегодня
fsqrt устарел. Расширение 3DNow! тоже устарело и больше не используется. Все процессоры x86-64 поддерживают как минимум SSE и SSE2. Большинство процессоров поддерживает AVX, а некоторые поддерживают AVX-512, но, например, GCC в настоящее время по умолчанию не генерирует команд AVX.p и s — это сокращения от «packed» и «scalar». Упакованные команды — это векторные команды SIMD, а скалярные работают за раз только с одним значением. Если ширина регистра, например, составляет 256 битов, то упакованная команда может выполнить параллельно s или d — это сокращение от степени точности «single» или «double» чисел с плавающей запятой. Так как мы имеем дело с аппроксимациями, то будем использовать числа с плавающей запятой с одинарной точностью. Можно использовать варианты ps или ss.Уже в 2009 году метод быстрого обратного квадратного корня с трудом можно было сравнить с командой
rsqrtss. А с тех пор в современных процессорах x86 было реализовано множество расширений со специализированными командами SIMD. То есть сегодня быстрый обратный квадратный корень не имеет никаких шансов и его время прошло?Почему бы не проверить это прямо сейчас: мы можем начать с выполнения тестов на моей машине с довольно современным процессором: AMD Zen 3 5950X, выпущенным в конце 2020 года.
Первоначальное тестирование
Мы напишем программу на C, которая будет пытаться вычислить обратный квадратный корень тремя разными способами:
-
exact: простым1.0 / sqrtf(x)с использованием функцииsqrtfиз стандартной библиотеки C, -
appr: первой аппроксимацией из исходного кода Q3, объяснённой выше, -
appr_nr: полной методикой Q3 с одной итерацией метода Ньютона-Рафсона.
При каждом методе мы выполним вычисление для каждого значения в рандомизированном входном массиве и измерим потраченное суммарно время. Чтобы получить время до и после вычислений, можно использовать функцию
clock_gettime из libc (для систем POSIX), а затем получить разность. Потом мы повторим это множество раз, чтобы снизить влияние случайных колебаний. Программа на C выглядит следующим образом:#include <stdlib.h>
#include <stdio.h>
#include <stdint.h>
#include <time.h>
#include <math.h>
#define N 4096
#define T 1000
#define E9 1000000000
#ifndef CLOCK_REALTIME
#define CLOCK_REALTIME 0
#endif
enum methods { EXACT, APPR, APPR_NR, M };
const char *METHODS[] = { "exact", "appr", "appr_nr" };
static inline float rsqrt_exact(float x) { return 1.0f / sqrtf(x); }
static inline float rsqrt_appr(float x) {
uint32_t i = *(uint32_t*)&x;
i = -(i >> 1) + 0x5f3759df;
return *(float*)&i;
}
static inline float rsqrt_nr(float x, float y) { return y * (1.5f - x*0.5f*y*y); }
static inline float rsqrt_appr_nr(float x) {
float y = rsqrt_appr(x);
return rsqrt_nr(x, y);
}
int main() {
srand(time(NULL));
float y_sum[M] = {0};
double t[M] = {0};
for (int trial = 0; trial < T; trial++) {
struct timespec start, stop;
float x[N], y[N];
for (int i = 0; i < N; i++) { x[i] = rand(); }
clock_gettime(CLOCK_REALTIME, &start);
for (int i = 0; i < N; i++) { y[i] = rsqrt_exact(x[i]); }
clock_gettime(CLOCK_REALTIME, &stop);
for (int i = 0; i < N; i++) { y_sum[EXACT] += y[i]; }
t[EXACT] += ((stop.tv_sec-start.tv_sec)*E9 + stop.tv_nsec-start.tv_nsec);
clock_gettime(CLOCK_REALTIME, &start);
for (int i = 0; i < N; i++) { y[i] = rsqrt_appr(x[i]); }
clock_gettime(CLOCK_REALTIME, &stop);
for (int i = 0; i < N; i++) { y_sum[APPR] += y[i]; }
t[APPR] += ((stop.tv_sec-start.tv_sec)*E9 + stop.tv_nsec-start.tv_nsec);
clock_gettime(CLOCK_REALTIME, &start);
for (int i = 0; i < N; i++) { y[i] = rsqrt_appr_nr(x[i]); }
clock_gettime(CLOCK_REALTIME, &stop);
for (int i = 0; i < N; i++) { y_sum[APPR_NR] += y[i]; }
t[APPR_NR] += ((stop.tv_sec-start.tv_sec)*E9 + stop.tv_nsec-start.tv_nsec);
}
printf("rsqrt\tps/op\tratio\terr\n");
for (int m = 0; m < M; m++) {
printf("%s\t%.0f\t%.2f\t%.4f\n",
METHODS[m],
t[m] * 1000.0f / N / T,
(double) t[EXACT] / t[m],
(y_sum[m] - y_sum[EXACT]) / y_sum[EXACT]);
}
return 0;
}В конце программы мы выводим три показателя для каждого метода:
- среднее время вычисления одной операции в пикосекундах, чем меньше, тем лучше,
- коэффициент времени вычислений по сравнению с точным методом, чем больше, тем быстрее,
- среднюю погрешность между методом и точным методом, просто чтобы убедиться, что вычисления выполнены правильно.
Чего же мы ожидаем? В наборе команд x86 есть специализированные функции для вычисления обратного квадратного корня, которые компилятор должен иметь возможность генерировать. Их скорость, вероятно, выше, чем метод аппроксимации, при котором мы выполняем несколько операций.
Давайте проверим это: сначала скомпилируем код при помощи GCC без любых оптимизаций, в явном виде задав
-O0. Так как мы используем math.h для точного метода, нам также понадобится скомпоновать математическую библиотеку при помощи -lm:$ gcc -lm -O0 rsqrt.c
$ ./a.out
rsqrt ps/op ratio err
exact 3330 1.00 0.0000
appr 2020 1.65 0.0193
appr_nr 6115 0.54 -0.0010Это кажется логичным. Погрешность заметна после первой аппроксимации, но уменьшается после одной итерации NR. Первая аппроксимация на самом деле быстрее точного метода, но совместно с одним шагом NR она вдвое медленнее. Метод NR требует требует количества операций больше разумного.
Но это лишь отладочная сборка, давайте попробуем добавлять оптимизации при помощи флага
-O3. Это включит все оптимизации, не противоречащие стандартам.$ gcc -lm -O3 rsqrt.c
$ ./a.out
rsqrt ps/op ratio err
exact 1879 1.00 0.0000
appr 72 26.01 0.0193
appr_nr 178 10.54 -0.0010Хм, теперь аппроксимации намного быстрее, чем раньше, однако время точного метода уменьшилось всего вдвое, поэтому аппроксимация с NR в десять с лишним раз быстрее точного метода. Возможно, компилятор не сгенерировал функции обратного квадратного корня? Может быть, ситуация улучшится, если мы используем флаг
-Ofast, описанный на man-странице gcc(1):Отключение строгого следования стандартам. -Ofast включает все оптимизации -O3. Также он включает оптимизации, валидные не для всех программ, соответствующих стандартам. Он включает -ffast-math, -fallow-store-data-races и специфичные для Fortran -fstack-arrays, если не задан fmax-stack-var-size, и -fno-protect-parens. Он отключает -fsemantic-interposition.
Наш точный метод может быть не таким точным, как раньше, но может оказаться быстрее.
$ gcc -lm -Ofast rsqrt.c
$ ./a.out
rsqrt ps/op ratio err
exact 153 1.00 0.0000
appr 118 1.30 0.0137
appr_nr 179 0.85 -0.0009И он действительно быстрее. Первая аппроксимация по-прежнему быстрее него, но с шагом NR она медленнее точного метода. Погрешность для аппроксимаций немного уменьшилась, потому что мы по-прежнему сравниваем с «точным» методом, который теперь даёт другие результаты. Довольно странно, что первая аппроксимация стала вдвое быстрее. Похоже, это особенность GCC, потому что Clang не имеет этой проблемы, а во всём остальном он создаёт схожие результаты:
$ clang -lm -O0 rsqrt.c
$ ./a.out
rsqrt ps/op ratio err
exact 3715 1.00 0.0000
appr 1933 1.92 0.0193
appr_nr 6001 0.62 -0.0010$ clang -lm -O3 rsqrt.c
$ ./a.out
rsqrt ps/op ratio err
exact 1900 1.00 0.0000
appr 61 31.26 0.0193
appr_nr 143 13.24 -0.0010
$ clang -lm -Ofast rsqrt.c
$ ./a.out
rsqrt ps/op ratio err
exact 148 1.00 0.0000
appr 62 2.40 0.0144
appr_nr 145 1.02 -0.0009Дизассемблирование
У обоих компиляторов есть достаточно большая разница между
-O3 и -Ofast. Чтобы разобраться в происходящем, мы можем посмотреть на дизассемблированный код. Чтобы получить в двоичном файле отладочные символы, сообщающие нам, какой объектный код соответствует исходному коду, нужно передать компилятору флаг -g. Затем мы можем выполнить objdump -d с флагом -S, чтобы увидеть дизассемблированные команды рядом с исходным кодом:$ gcc -lm -O3 -g rsqrt.c
$ objdump -d -S a.out
...
static inline float rsqrt_exact(float x) { return 1.0f / sqrtf(x); }
118e: 66 0f ef db pxor %xmm3,%xmm3
1192: 0f 2e d8 ucomiss %xmm0,%xmm3
1195: 0f 87 e1 02 00 00 ja 147c <main+0x3bc>
119b: f3 0f 51 c0 sqrtss %xmm0,%xmm0
119f: f3 0f 10 0d 99 0e 00 movss 0xe99(%rip),%xmm1 # 2040
11a6: 00
...
11ab: f3 0f 5e c8 divss %xmm0,%xmm1
...
2040: 00 00 80 3f 1.0fЭто синтаксис AT&T для ассемблерного кода x86-64. Обратите внимание, что операнд источника всегда находится перед операндом назначения. Скобки обозначают адрес, например,
movss 0xecd(%rip),%xmm1 копирует значение, расположенное на 0xecd байтов перед адресом в регистре rip (указателе команд, или PC), в регистр xmm1. Регистры xmmN имеют ширину 128 битов или 4 слова. Однако команды ss предназначены для скалярных значений одинарной точности, поэтому команда применит операцию только к одному значению с плавающей запятой в самых младших 32 битах.В случае
-O3 мы используем скалярную sqrtss, за которой следует divss. Также присутствует сравнение ucomiss и переход ja, переводящий errno в режим EDOM в случае, если входящие данные меньше -0. Мы совершенно не используем errno, поэтому можно удалить присвоение значения errno, задав флаг -fno-math-errno:$ gcc -lm -O3 -g -fno-math-errno rsqrt.c
$ ./a.out
rsqrt ps/op ratio err
exact 479 1.00 0.0000
appr 116 4.13 0.0193
appr_nr 175 2.74 -0.0010$ objdump -d -S a.out
...
static inline float rsqrt_exact(float x) { return 1.0f / sqrtf(x); }
1170: 0f 51 0c 28 sqrtps (%rax,%rbp,1),%xmm1
1174: f3 0f 10 1d c4 0e 00 movss 0xec4(%rip),%xmm3 # 2040
117b: 00
117c: 48 83 c0 10 add $0x10,%rax
1180: 0f c6 db 00 shufps $0x0,%xmm3,%xmm3
1184: 0f 28 c3 movaps %xmm3,%xmm0
1187: 0f 5e c1 divps %xmm1,%xmm0
...
2040: 00 00 80 3f 1.0fЭто позволяет нам не проверять каждое входное значение по отдельности, обеспечивая таким образом возможность использовать упакованные вариации команд, выполняя по четыре операции за раз. Это сильно повышает производительность. Однако мы по-прежнему используем
sqrtps, за которым следует divps. Также нам придётся включить -funsafe-math-optimizations4 и -ffinite-math-only, чтобы заставить GCC генерировать rsqrtps. Тогда мы получим код, аналогичный тому, когда использовали -Ofast:4Это включает в себя
-fno-signed-zeros, -fno-trapping-math, -fassociative-math и -freciprocal-math. Я попытался включить их все по отдельности, но не смог получить команды rsqrtps, пока не включил -funsafe-math-optimizations. Похоже, эта опция делает нечто большее, чем включение этих флагов.$ gcc -lm -O3 -g -fno-math-errno -funsafe-math-optimizations -ffinite-math-only rsqrt.c
$ ./a.out
rsqrt ps/op ratio err
exact 155 1.00 0.0000
appr 120 1.29 0.0137
appr_nr 182 0.85 -0.0009$ objdump -d -S a.out
...
static inline float rsqrt_exact(float x) { return 1.0f / sqrtf(x); }
1170: 0f 52 0c 28 rsqrtps (%rax,%rbp,1),%xmm1
1174: 0f 28 04 28 movaps (%rax,%rbp,1),%xmm0
1178: 48 83 c0 10 add $0x10,%rax
117c: 0f 59 c1 mulps %xmm1,%xmm0
117f: 0f 59 c1 mulps %xmm1,%xmm0
1182: 0f 59 0d c7 0e 00 00 mulps 0xec7(%rip),%xmm1 # 2050
1189: 0f 58 05 b0 0e 00 00 addps 0xeb0(%rip),%xmm0 # 2040
1190: 0f 59 c1 mulps %xmm1,%xmm0
...
2040: 00 00 40 c0 -3.0f
...
2050: 00 00 00 bf -0.5fТеперь в коде используется
rsqrtps, но в нём есть множество команд умножения, а также сложения. Зачем они нужны, разве нам не требуется только обратный квадратный корень? Мы можем получить подсказку, взглянув на дизассемблированный код функции appr_nr:static inline float rsqrt_nr(float x, float y) { return y * (1.5f - x*0.5f*y*y); }
12f8: f3 0f 10 1d 80 0d 00 movss 0xd80(%rip),%xmm3 # 2080
12ff: 00
...
1304: 0f 59 05 65 0d 00 00 mulps 0xd65(%rip),%xmm0 # 2070
...
1310: 0f c6 db 00 shufps $0x0,%xmm3,%xmm3
...
1318: 0f 28 d1 movaps %xmm1,%xmm2
131b: 0f 59 d1 mulps %xmm1,%xmm2
131e: 0f 59 d0 mulps %xmm0,%xmm2
1321: 0f 28 c3 movaps %xmm3,%xmm0
1324: 0f 5c c2 subps %xmm2,%xmm0
1327: 0f 59 c1 mulps %xmm1,%xmm0
...
2070: 00 00 00 3f 0.5f
...
2080: 00 00 c0 3f 1.5fПоследняя часть выглядит очень похожей, потому что на самом деле выполняет то же самое: итерацию метода Ньютона-Рафсона5. Это можно понять из man-страницы gcc(1):
5Компилятор выполнил операции немного в другом порядке. Похоже, он вычисляет это как
-0.5f*y*(x*y*y+-3.0f).Эта опция включает использование команд приблизительного обратного значения и приблизительного обратного квадратного корня с дополнительными шагами метода Ньютона-Рафсона для повышения точности вместо выполнения деления или квадратного корня и деления для получения аргументов с плавающей запятой.
Команда
rsqrtps гарантирует только относительную погрешность меньше Если нам не нужна дополнительная точность, можно ли обеспечить ускорение, пропустив этап NR? Можно использовать встроенные функции компилятора, чтобы заставить компилятор сгенерировать только команду
rsqrtps. В руководстве по GCC есть список встроенных функции для набора команд x86. Существует функция __builtin_ia32_rsqrtps, генерирующая команду rsqrtps:v4sf __builtin_ia32_rsqrtps (v4sf);В руководстве также есть глава о том, как использовать эти векторные команды со встроенными функциями. Нам нужно добавить
typedef для типа v4sf, содержащего четыре числа с плавающей запятой. Затем можно использовать массив float в указатель vfs4. Мы добавим эти части в свою предыдущую программу:typedef float v4sf __attribute__ ((vector_size(16)));
v4sf rsqrt_intr(v4sf x) { return __builtin_ia32_rsqrtps(x); };
v4sf *xv = (v4sf*)x, *yv = (v4sf*)y;
clock_gettime(CLOCK_REALTIME, &start);
for (int i = 0; i < N/4; i++) { yv[i] = rsqrt_intr(xv[i]); }
clock_gettime(CLOCK_REALTIME, &stop);
for (int i = 0; i < N; i++) { y_sum[INTR] += y[i]; }
t[INTR] += ((stop.tv_sec-start.tv_sec)*E9 + stop.tv_nsec-start.tv_nsec);Можно скомпилировать этот код, чтобы запустить и дизассемблировать его:
$ gcc -lm -O3 -g rsqrt_vec.c
$ ./a.out
rsqrt ps/op ratio err
exact 1895 1.00 0.0000
appr 72 26.39 0.0193
appr_nr 175 10.81 -0.0010
rsqrtps 61 31.00 0.0000$ objdump -d -S a.out
...
v4sf rsqrt_intr(v4sf x) { return __builtin_ia32_rsqrtps(x); };
1238: 41 0f 52 04 04 rsqrtps (%r12,%rax,1),%xmm0
...Мы уменьшили код до одной команды, и он стал чуть быстрее, чем раньше.
Существуют также расширения, поддерживаемые не всеми процессорами, которые мы можем попробовать применить. При помощи
-march=native мы можем приказать компилятору использовать любые команды, которые есть в нашем процессоре. Однако это сделает двоичный файл несовместимым с другими процессорами.$ gcc -lm -Ofast -g -march=native rsqrt_vec.c
$ ./a.out
rsqrt ps/op ratio err
exact 78 1.00 0.0000
appr 40 1.96 0.0137
appr_nr 85 0.91 -0.0009
rsqrtps 62 1.25 0.0000Теперь мы оптимизировались почти до уровня первой аппроксимации. Встроенная функция по скорости примерно такая же. «Точный» метод мы заменили 256-битной
vrsqrtps и одним шагом NR:static inline float rsqrt_exact(float x) { return 1.0f / sqrtf(x); }
11d0: c5 fc 52 0c 18 vrsqrtps (%rax,%rbx,1),%ymm1
11d5: c5 f4 59 04 18 vmulps (%rax,%rbx,1),%ymm1,%ymm0
11da: 48 83 c0 20 add $0x20,%rax
11de: c4 e2 75 a8 05 79 0e vfmadd213ps 0xe79(%rip),%ymm1,%ymm0
11e5: 00 00
11e7: c5 f4 59 0d 91 0e 00 vmulps 0xe91(%rip),%ymm1,%ymm1
11ee: 00
11ef: c5 fc 59 c1 vmulps %ymm1,%ymm0,%ymm0Теперь
__builtin_ia32_rsqrtps использует одну vrsqrtps без шага NR, однако она по-прежнему использует только 128-битные регистры.Быстрая обработка
Итак, мы провели тестирование на моей машине и получили представление о том, какие виды команд можно использовать для вычисления обратного квадратного корня и какая производительность у них может быть. Теперь мы попробуем выполнить эти бенчмарки на множестве разных машин, чтобы понять, как наши открытия применимы в общем случае. Это те машины, к которым у меня есть удобный SSH-доступ. Все полученные данные можно скачать отсюда, в них также включены результаты по отдельности для функций обратного значения и квадратного корня.
Ниже показан список протестированных x86-машин, с указанием их CPU и даты выпуска. Все предыдущие тесты выполнялись на компьютере «igelkott».
| Имя хоста | Семейство CPU | Модель CPU | Год | Форм-фактор |
|---|---|---|---|---|
| jackalope | Core | Intel Celeron 550 | 2007 | Ноутбук с i686 |
| narwhal | Piledriver | AMD FX-6300 | 2012 | Десктоп с x86_64 |
| silverback | Ivy Bridge | Intel Xeon E5-1410 | 2014 | Сервер с x86_64 |
| bovinae | Kaby Lake | Intel Core i5-8250U | 2017 | Ноутбук с x86_64 |
| igelkott | Zen 3 | AMD Ryzen 5950X | 2020 | Десктоп с x86_64 |
| deck | Zen 2 | AMD APU 0405 | 2022 | Мобильное устройство с x86_64 |
Ниже представлен график соотношений производительности по сравнению с точным методом
exact, то есть время каждого метода, разделённое на время метода exact. Чем выше коэффициент, тем выше производительность, всё, что ниже 1, медленнее exact, а всё, что выше, — быстрее. Здесь мы использовали флаг -Ofast, потому что это самая быстрая опция, которую можно использовать без ущерба для портируемости.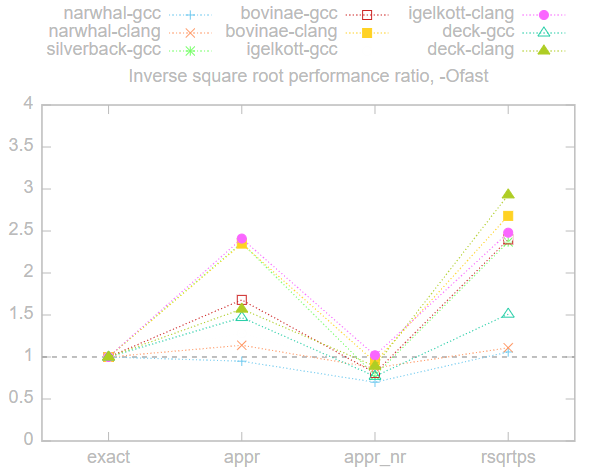
Результаты довольно схожи на всех машинах, время методов приблизительно ранжировано в порядке
rsqrtps <= appr < exact <= appr_nr. Применение метода appr_nr или медленнее, или схоже с методом exact, то есть в данном случае не даёт реальной выгоды.Машина «jackalope» не включена в показанный выше график, потому что метод
exact был на ней чрезвычайно медленным. Особенно когда не использовался -march=native, потому что компилятор в таком случае откатывался к применению древней команды fsqrt.Ниже представлена таблица таймингов при использовании
-Ofast, числа в скобках получения при использовании -march=native. Каждое число определяет, сколько отдельная операция занимает времени в пикосекундах.| Машина/компилятор | exact | appr | appr_nr | rsqrtps |
|---|---|---|---|---|
| jackalope-clang | 53634 (5363) | 1500 (2733) | 4971 (3996) | N/A |
| narwhal-gcc | 419 (363) | 443 (418) | 601 (343) | 396 (231) |
| narwhal-clang | 389 (796) | 340 (321) | 445 (859) | 349 (388) |
| silverback-gcc | 422 (294) | 179 (199) | 543 (543) | 178 (189) |
| bovinae-gcc | 260 (127) | 155 (81) | 321 (119) | 108 (105) |
| bovinae-clang | 255 (132) | 108 (78) | 272 (112) | 95 (96) |
| igelkott-gcc | 141 (79) | 111 (63) | 168 (87) | 58 (64) |
| igelkott-clang | 152 (76) | 63 (40) | 149 (70) | 61 (62) |
| deck-gcc | 342 (160) | 234 (114) | 444 (172) | 226 (120) |
| deck-clang | 297 (166) | 189 (123) | 332 (140) | 101 (126) |
Функция квадратного корня даёт немного иные результаты:

Довольно странно, что встроенная функция
sqrtps медленнее, чем метод exact, а appr без NR теперь быстрее. Метод appr_nr по-прежнему не даёт никаких преимуществ, он стабильно хуже exact.Вот исходные тайминги для функции квадратного корня с
-Ofast. Числа в скобках снова указаны для -march=native:| Машина/компилятор | exact | appr | appr_nr | sqrtps |
|---|---|---|---|---|
| jackalope-clang | 35197 (5743) | 1494 (2738) | 19191 (4308) | N/A |
| narwhal-gcc | 505 (399) | 399 (427) | 659 (559) | 796 (785) |
| narwhal-clang | 448 (823) | 327 (319) | 638 (847) | 803 (780) |
| silverback-gcc | 625 (297) | 271 (190) | 958 (728) | 1163 (1135) |
| bovinae-gcc | 301 (148) | 155 (81) | 408 (200) | 225 (226) |
| bovinae-clang | 315 (244) | 92 (60) | 399 (159) | 317 (227) |
| igelkott-gcc | 173 (95) | 119 (38) | 233 (124) | 288 (296) |
| igelkott-clang | 168 (143) | 63 (48) | 234 (104) | 170 (283) |
| deck-gcc | 419 (205) | 215 (108) | 519 (252) | 575 (574) |
| deck-clang | 325 (244) | 153 (88) | 372 (180) | 315 (458) |
Как указал пользователь thegeomaster, в некоторых случаях может требоваться детерминированность, то есть гарантия, что на разных машинах будет получаться одинаковый результат. Команда
rsqrtps требуется только для того, чтобы относительная погрешность была меньше 6Согласно исследованию Роберта О’Каллахана, реализации команд rsqrt в AMD и Intel отличаются для ровно 22 из
Однако в спецификации IEEE 754 есть спецификация для функции квадратного корня, которой гарантированно соответствует функция
sqrtps. Поэтому в лучшем случае мы можем использовать sqrtps, за которой следует divps — именно это мы получили при использовании -O3 и -fno-math-errno. Воспроизводимость мы потеряли, только когда добавили -funsafe-math-optimzations. Если воспроизводимость обязательна, то при честном сравнении следует использовать только операции с плавающей запятой, соответствующие требованиям IEEE-754: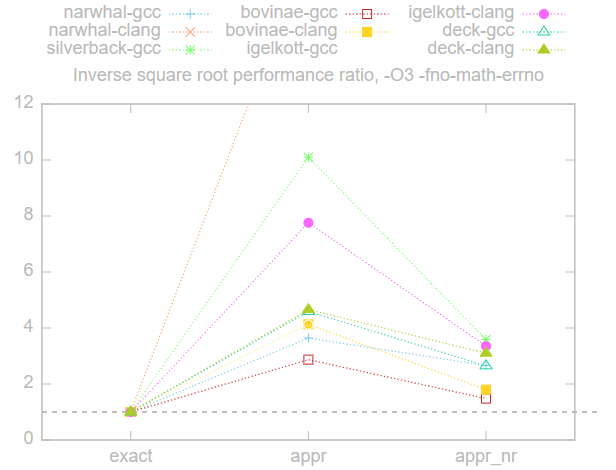
Это сдвигает чашу весов в пользу аппроксимаций. Применение метода
appr_nr приводит к реализации, которая в 2-4 раза быстрее метода exact. Здесь narwhal-clang стал выбросом из-за удивительно медленного метода exact.Попробуйте самостоятельно
Можете попробовать запустить бенчмарки на своей машине и проверить, получите ли вы схожие результаты. Есть шелл-скрипт
bench/run.sh, который генерирует и запускает бенчмарки при помощи файла bench/bench.c.m4. Эти файлы можно найти в репозитории этой статьи. Просто запустите скрипт без аргументов, и он сгенерирует файл .tsv со всеми результатами:$ cd bench
$ sh run.sh
$ grep rsqrt bench.tsv | sort -nk3 | head
rsqrt appr 40 1.91 0.0139 clang-Ofast-march=native
rsqrt rsqrtps 56 32.08 0.0000 clang-O3
rsqrt appr 58 31.08 0.0193 clang-O3
rsqrt rsqrtps 58 2.48 0.0000 clang-O3-fno-math-errno-funsafe-math-optimizations-ffinite-math-only
rsqrt rsqrtps 59 2.45 0.0000 gcc-Ofast
rsqrt rsqrtps 59 2.48 0.0000 clang-Ofast
rsqrt rsqrtps 59 31.07 0.0000 gcc-O3
rsqrt rsqrtps 59 7.83 0.0000 gcc-O3-fno-math-errno
rsqrt appr 60 2.41 0.0144 clang-O3-fno-math-errno-funsafe-math-optimizations-ffinite-math-only
rsqrt rsqrtps 60 8.09 0.0000 clang-O3-fno-math-errnoВ заключение
Подведём итог: использование простого
1/sqrtf(x) на современных процессорах x86 может быть и быстрее, и точнее, чем метод быстрого обратного квадратного корня из функции Q_rsqrt игры Quake III.Однако основной вывод заключается в том, что необходимо приказать компилятору сделать его быстрее. При простой компиляции с помощью
-O3 метод быстрого обратного квадратного корня на самом деле существенно быстрее, чем наивная реализация. Нам придётся позволить компилятору нарушить строгие требования спецификации, чтобы он сгенерировал более быструю реализацию.Как говорилось в обсуждениях на HN, в некоторых случаях обязательным требованием становится детерминированность, то есть воспроизводимость между разными машинами. В таком случае мы можем использовать только те операции с плавающей запятой, которые детерминированы по стандартам, а к команде
rqsrtps это неприменимо. Для таких случаев метод быстрого обратного квадратного корня может быть в 2-4 раза быстрее наивной реализации.Если допустима очень низкая точность, то можно получить чуть более быструю реализацию, пропустив этап метода Ньютона-Рафсона из метода быстрого обратного квадратного корня. Любопытно, что компилятор тоже выполняет шаг NR после использования реализаций аппроксимаций обратного квадратного корня. Их тоже можно чуть ускорить, пропустив шаг NR, просто сгенерировав команду аппроксимации с помощью встроенных функций компилятора.
В этом посте мы рассматривали x86, но что насчёт других наборов команд?7 Метод быстрого обратного квадратного корня может по-прежнему быть полезен для процессоров без специализированных команд квадратного корня.
7Я провёл быстрые тесты на своём телефоне с armv7 phone; скорость
appr_nr была схожа со скоростью exact. Также я попробовал запустить тесты на машине с MIPS32, но столкнулся с проблемами в тулчейне кросс-компиляции. Оставим это на следующий раз...Как обычно реализуются аппаратные реализации приблизительных квадратных корней? Может ли приблизительная аппаратная реализация потенциально использовать нечто похожее на первую аппроксимацию быстрого обратного квадратного корня?

