Мы знакомы с головоломкой кубик Рубика, но, проживая в трёхмерном пространстве, трудно представить себе такую в четырёхмерном. Разумеется, Рубик не патентовал четырёхмерных кубиков, и речь идёт лишь о подобии кубика Рубика.
Поэтому сперва я расскажу о том, как я себе представляю четырёхмерную головоломку.
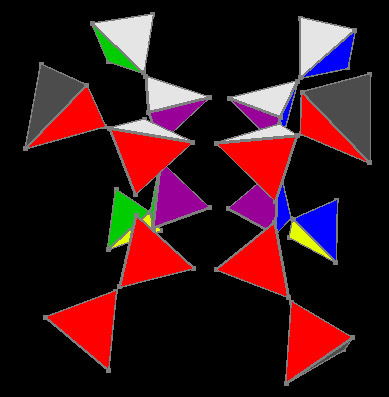
Для начала представим себе, каким образом получается трёхмерный куб. Возьмём одномерное пространство: всё, что мы можем в нём изображать, ограничивается одномерными объектами, такими как точка, отрезок, луч, прямая. Нарисуем отрезок единичной длины AB [0,1]. Теперь добавим второе измерение: ось ординат будет направлена вверх, а наш единичный отрезок AB лежит на оси абсцисс, в декартовой системе координат.
Пожалуй, двумерное пространство наиболее привычно для человеческого понимания, потому что ни сферу, ни куб, нарисовать не получится, мы привыкли их изображать как проекцию на плоскость. Хорошо, с двумерным пространством у нас проблем нет, поэтому давайте вдумаемся как получается квадрат. Значит, берём мы отрезок AB (вершины A(0,0) и B(1,0)) на оси абсцисс, отступаем ровно единицу по оси ординат и дублируем отрезок, назовём его CD, с точками C(0,1) и D(1,1).
Чтобы получить квадрат, нам теперь нужно соединить соответствующие вершины, то есть вершину A(0,0) соединяем с её дубликатом C(0,1), а вершину B(1,0) соединяем с D(1,1). Теперь мы имеем квадрат ACDB. Поняв как это работает в двумерном пространстве, будет довольно просто понять как получается куб в трёхмерном. Итак по пунктам:
1. Добавляем третье измерение, ось аппликат будет направлена в глубину.
2. Дублируем ACDB отступив на единицу по оси аппликат, вершины трансформируются так:
A(0,0,0) -> H(0,0,1)
C(0,1,0) -> F(0,1,1)
D(1,1,0) -> G(1,1,1)
B(1,0,0) -> E(1,0,1)
3. Соединяем соответствующие вершины квадратов.
Теперь читатель морально готов увидеть тессеракт:
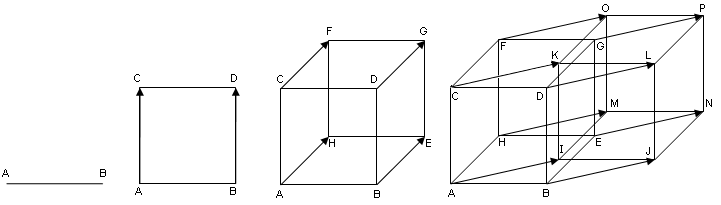
По сути мы дублируем куб, смещая по оси четвёртого измерения, и соединяем соответствующие вершины — проще не придумаешь. Для наглядности мы будем увеличивать дубликат куба, помещая первоначальный куб внутрь него. Вот такое изображение чаще всего применяется при попытке спроецировать тессеракт на плоскость:

Чтобы подчеркнуть, что все отрезки у тессеракта единичные и показать равноправность проецирования, четырёхмерный куб можно изобразить анимацией:

Но это всё присказка, а сказка впереди!
Теперь давайте разберёмся, что есть четырёхмерная головоломка, а главное как её изобразить.
Как известно, у куба шесть граней, следовательно, у трёхмерной головоломки 6 цветов. Чтобы упростить себе жизнь, мы будем работать с кубиком 2х2х2, в частности, нам будет очень полезно то, что перестановок у такого кубика всего 3^6 * 7! = 3674160.

Перечислим грани:
— По оси абсцисс Left-Right, цвета зелёный-синий.
— По оси ординат Down-Up, цвета жёлтый-белый.
— По оси аппликат Front-Back, цвета красный-оранжевый.
Включаем warp drive и открываем червоточину в четвёртое измерение!
Вот так изображают четырёхмерную головоломку зарубежные математики:
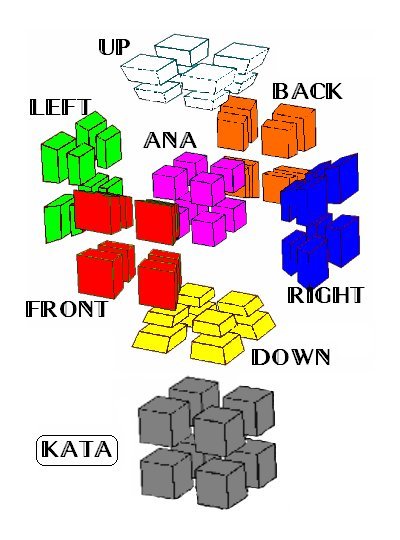
То есть по сути мы просто взяли трёхмерный кубик 2х2х2, добавили ось в четвёртое измерение и получили четвёртую строчку:
— По оси четвёртого измерения Ana-Kata, цвета пурпурный-серый.
Нужно заметить, что теперь все группы из 8 цветов являются трёхмерными гипергранями, а не двумерными гранями (которые имели по 4 цвета). Теперь, как представляю точно такой же (математически эквивалентный) четырёхмерный кубик я:

Если взять внутреннюю часть головоломки (то есть кубик, состоящий из 8 трёхцветных углов), то мы просто вырезали из трёхмерного кубика октаэдр и внутреннюю вырезанную поверхность окрасили в пурпурный цвет, в результате углы кубика стали тетраэдрами, окрашенными в 4 цвета. Потом мы продублировали все углы кубика, развернули внутреннюю грань тетраэдров наружу и окрасили её в серый цвет, получив в результате мою прелесть .
Конечно, основная сложность моей работы заключалась не в том, чтобы, используя OpenGL, написать на Delphi программу, изображающую проэкцию четырёхмерной головоломки, а в разработке алгоритма решения такой головоломки. То есть у меня была идея, математическое представление, а OpenGL был единственным знакомым мне средством для изображения трёхмерной графики.
Сейчас мы рассмотрим что такое поворот гиперграни. В описанной головоломке есть всего 8 гиперграней, каждая из них является кубом. Поворот гиперграни по сути является поворотом одного куба относительно другого. Например, левый куб относительно правого, или внутренний относительно внешнего. Вариантов повернуть куб 24, потому что каждую из 6 граней можно повернуть одной из 4 сторон. Таких кубов у нас 8, значит за один ход мы имеем 192 инварианта расположения элементов головоломки. Я приведу лишь несколько из них ниже, под спойлером.
Основная последовательность сборки заключалась в следующем:
1. Эвристический метод, который размещает элементы с серыми цвета на позиции внешней гиперграни, называемой Kata, соответсвенно, все элементы с пурпурными цветами после этого этапа окажутся во внутренней гиперграни Ana.
2. Ориентирование серых цветов внешней гиперграни наружу.
3. Ориентирование пурпурных цветов внутренней гиперграни внутрь.
4. Размещение элементов внешней гиперграни по таблице решений трёхмерного кубика 2х2х2 (которых всего 3674160).
5. Размещение элементов внутренней гиперграни по той же таблице решений.
По первому пункту особых сложностей не было, чтобы разместить серые снаружи, пурпурные внутри достаточно было простого перебора, ну может слегка оптимизированного, вся суть алгоритма выглядит примерно покрутим этим боком, покрутим другим, переставим ещё пару раз, о, готово!
Второй этап имел алгоритмическую сложность O(192^3), но всего лишь 256 инвариантов, поэтому решено было составить перманентную таблицу с заранее вычисленными комбинациями решений (по сути аналог OLL в методе Фридрих для кубика Рубика). Составляет максимум 6 ходов.
Третий этап хоть и решался точно как второй, но экспоненциальная сложность порядка O(192^4) приводила к двухсуточным переборам, а количество инвариантов уже составляло 65536. Составляет максимум 8 ходов.
Зато после ориентирования цветов на гипергранях Ana-Kata мы сводим задачу к трёхмерному кубику. Четвёртый этап использует таблицу из 3674160 инвариантов, решение трёхмерного куба составляет максимум 11 ходов. Итак внежний гиперкуб собран.
Для пятого этапа мы используем те же решения трёхмерного куба, за тем лишь исключением, что для каждого поворота какой-либо грани внутренний кубик поворачивается нужным боком относительно внешнего для каждого поворота, в результате внешняя, уже собранная, гипергрань вращает только свою правую часть и остаётся всегда почти собранной.
То есть, используя таблицы, компьютер теперь обходился микросекундами на поиск, да вот только кэширование таблицы с HDD в оперативку отнимает несколько минут при инициализации программы. Ну и при наличии сразу трех таблиц с предрасчётами, алгоритм сборки уже не кажется сложным.
Поэтому сперва я расскажу о том, как я себе представляю четырёхмерную головоломку.

Тессеракт
Для начала представим себе, каким образом получается трёхмерный куб. Возьмём одномерное пространство: всё, что мы можем в нём изображать, ограничивается одномерными объектами, такими как точка, отрезок, луч, прямая. Нарисуем отрезок единичной длины AB [0,1]. Теперь добавим второе измерение: ось ординат будет направлена вверх, а наш единичный отрезок AB лежит на оси абсцисс, в декартовой системе координат.
Пожалуй, двумерное пространство наиболее привычно для человеческого понимания, потому что ни сферу, ни куб, нарисовать не получится, мы привыкли их изображать как проекцию на плоскость. Хорошо, с двумерным пространством у нас проблем нет, поэтому давайте вдумаемся как получается квадрат. Значит, берём мы отрезок AB (вершины A(0,0) и B(1,0)) на оси абсцисс, отступаем ровно единицу по оси ординат и дублируем отрезок, назовём его CD, с точками C(0,1) и D(1,1).
Чтобы получить квадрат, нам теперь нужно соединить соответствующие вершины, то есть вершину A(0,0) соединяем с её дубликатом C(0,1), а вершину B(1,0) соединяем с D(1,1). Теперь мы имеем квадрат ACDB. Поняв как это работает в двумерном пространстве, будет довольно просто понять как получается куб в трёхмерном. Итак по пунктам:
1. Добавляем третье измерение, ось аппликат будет направлена в глубину.
2. Дублируем ACDB отступив на единицу по оси аппликат, вершины трансформируются так:
A(0,0,0) -> H(0,0,1)
C(0,1,0) -> F(0,1,1)
D(1,1,0) -> G(1,1,1)
B(1,0,0) -> E(1,0,1)
3. Соединяем соответствующие вершины квадратов.
Теперь читатель морально готов увидеть тессеракт:
По сути мы дублируем куб, смещая по оси четвёртого измерения, и соединяем соответствующие вершины — проще не придумаешь. Для наглядности мы будем увеличивать дубликат куба, помещая первоначальный куб внутрь него. Вот такое изображение чаще всего применяется при попытке спроецировать тессеракт на плоскость:

Чтобы подчеркнуть, что все отрезки у тессеракта единичные и показать равноправность проецирования, четырёхмерный куб можно изобразить анимацией:

Но это всё присказка, а сказка впереди!
От тессеракта к головоломке
Теперь давайте разберёмся, что есть четырёхмерная головоломка, а главное как её изобразить.
Как известно, у куба шесть граней, следовательно, у трёхмерной головоломки 6 цветов. Чтобы упростить себе жизнь, мы будем работать с кубиком 2х2х2, в частности, нам будет очень полезно то, что перестановок у такого кубика всего 3^6 * 7! = 3674160.

Перечислим грани:
— По оси абсцисс Left-Right, цвета зелёный-синий.
— По оси ординат Down-Up, цвета жёлтый-белый.
— По оси аппликат Front-Back, цвета красный-оранжевый.
Включаем warp drive и открываем червоточину в четвёртое измерение!
Вот так изображают четырёхмерную головоломку зарубежные математики:

То есть по сути мы просто взяли трёхмерный кубик 2х2х2, добавили ось в четвёртое измерение и получили четвёртую строчку:
— По оси четвёртого измерения Ana-Kata, цвета пурпурный-серый.
Нужно заметить, что теперь все группы из 8 цветов являются трёхмерными гипергранями, а не двумерными гранями (которые имели по 4 цвета). Теперь, как представляю точно такой же (математически эквивалентный) четырёхмерный кубик я:

Если взять внутреннюю часть головоломки (то есть кубик, состоящий из 8 трёхцветных углов), то мы просто вырезали из трёхмерного кубика октаэдр и внутреннюю вырезанную поверхность окрасили в пурпурный цвет, в результате углы кубика стали тетраэдрами, окрашенными в 4 цвета. Потом мы продублировали все углы кубика, развернули внутреннюю грань тетраэдров наружу и окрасили её в серый цвет, получив в результате мою прелесть .
Конечно, основная сложность моей работы заключалась не в том, чтобы, используя OpenGL, написать на Delphi программу, изображающую проэкцию четырёхмерной головоломки, а в разработке алгоритма решения такой головоломки. То есть у меня была идея, математическое представление, а OpenGL был единственным знакомым мне средством для изображения трёхмерной графики.
Гипергрань
Сейчас мы рассмотрим что такое поворот гиперграни. В описанной головоломке есть всего 8 гиперграней, каждая из них является кубом. Поворот гиперграни по сути является поворотом одного куба относительно другого. Например, левый куб относительно правого, или внутренний относительно внешнего. Вариантов повернуть куб 24, потому что каждую из 6 граней можно повернуть одной из 4 сторон. Таких кубов у нас 8, значит за один ход мы имеем 192 инварианта расположения элементов головоломки. Я приведу лишь несколько из них ниже, под спойлером.
Повороты гиперграней
Поворот внутренней гиперграни.

Поворот передней гиперграни.

Обратите внимание, это только один поворот: вначале куб направяется нужной гранью вниз, затем поворачивается вокруг вертикальной оси нужной стороной. Вот так формируются по 24 поворота на каждую гипергрань.

Поворот внутренней гиперграни.

Поворот передней гиперграни.

Обратите внимание, это только один поворот: вначале куб направяется нужной гранью вниз, затем поворачивается вокруг вертикальной оси нужной стороной. Вот так формируются по 24 поворота на каждую гипергрань.
Сборка
Перемешанный кубик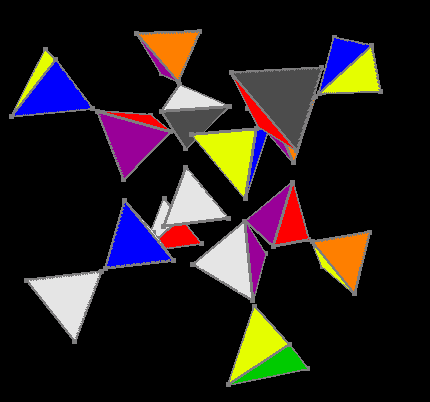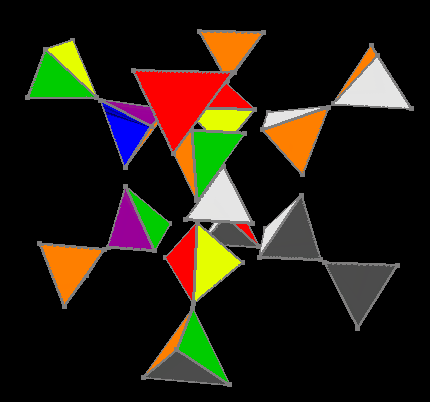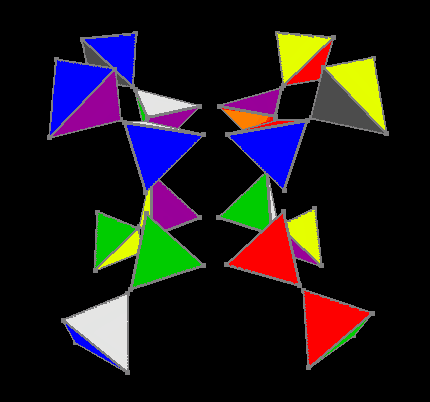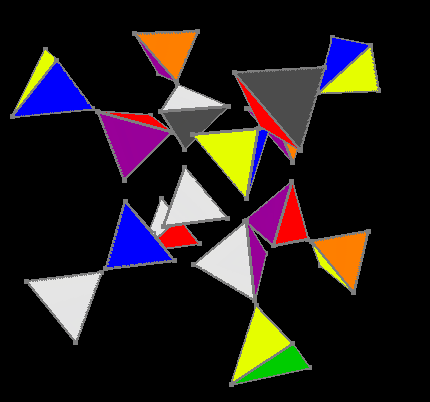
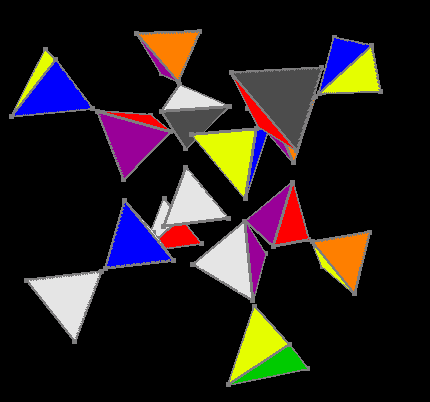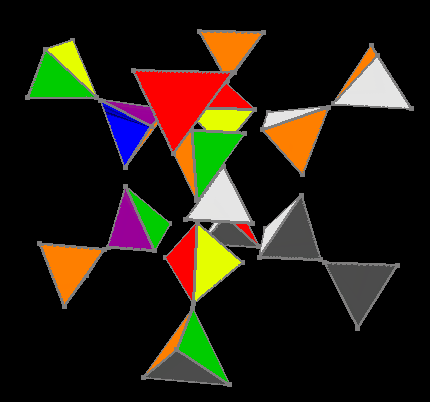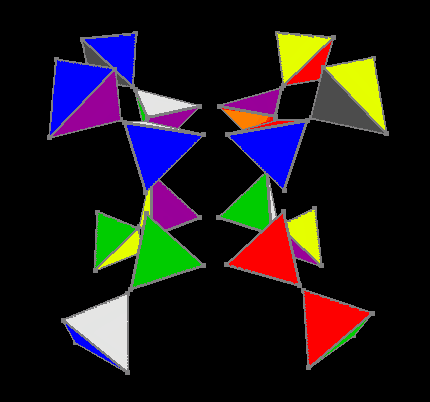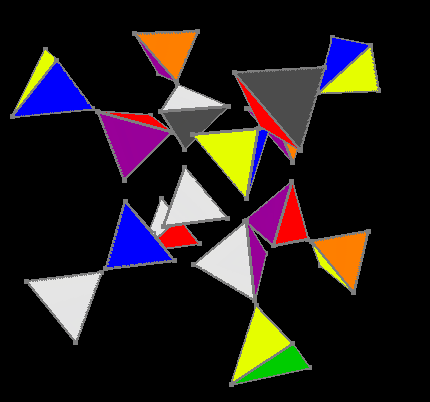
Основная последовательность сборки заключалась в следующем:
1. Эвристический метод, который размещает элементы с серыми цвета на позиции внешней гиперграни, называемой Kata, соответсвенно, все элементы с пурпурными цветами после этого этапа окажутся во внутренней гиперграни Ana.
2. Ориентирование серых цветов внешней гиперграни наружу.
3. Ориентирование пурпурных цветов внутренней гиперграни внутрь.
4. Размещение элементов внешней гиперграни по таблице решений трёхмерного кубика 2х2х2 (которых всего 3674160).
5. Размещение элементов внутренней гиперграни по той же таблице решений.
По первому пункту особых сложностей не было, чтобы разместить серые снаружи, пурпурные внутри достаточно было простого перебора, ну может слегка оптимизированного, вся суть алгоритма выглядит примерно покрутим этим боком, покрутим другим, переставим ещё пару раз, о, готово!
Второй этап имел алгоритмическую сложность O(192^3), но всего лишь 256 инвариантов, поэтому решено было составить перманентную таблицу с заранее вычисленными комбинациями решений (по сути аналог OLL в методе Фридрих для кубика Рубика). Составляет максимум 6 ходов.
Третий этап хоть и решался точно как второй, но экспоненциальная сложность порядка O(192^4) приводила к двухсуточным переборам, а количество инвариантов уже составляло 65536. Составляет максимум 8 ходов.
Ориентированы внешние и внутренние цвета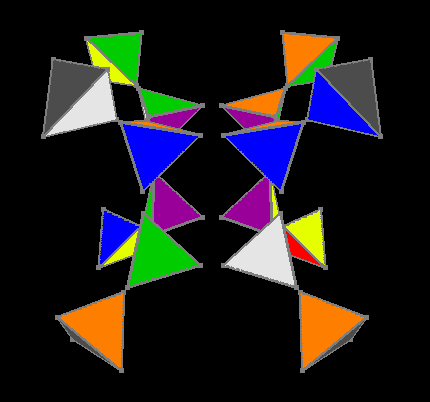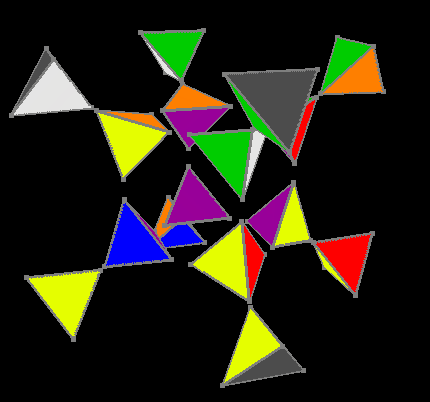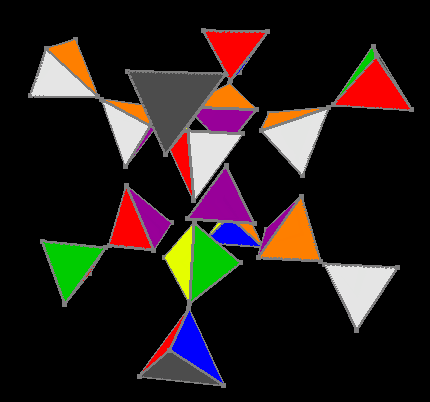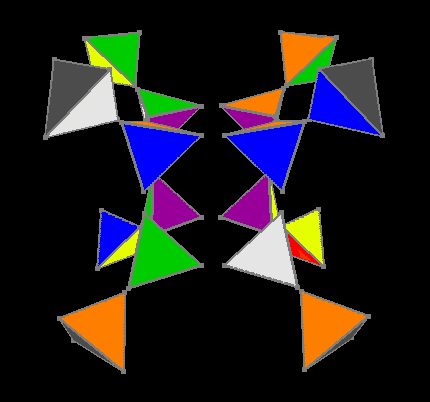
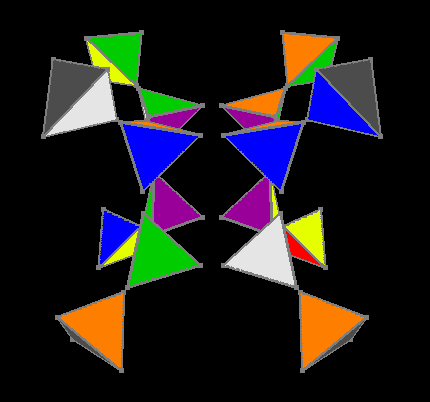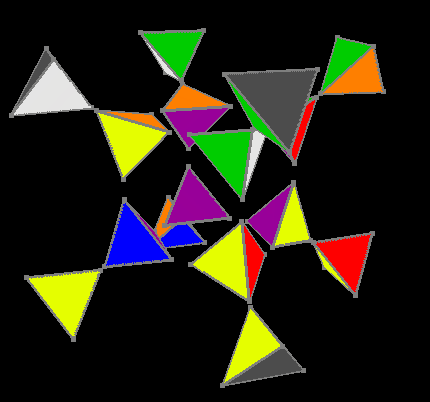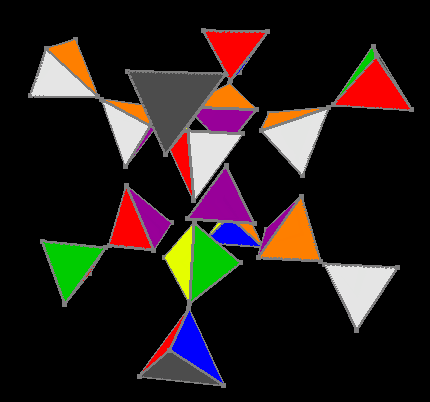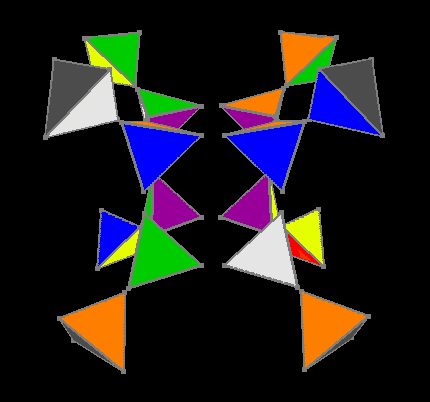
Зато после ориентирования цветов на гипергранях Ana-Kata мы сводим задачу к трёхмерному кубику. Четвёртый этап использует таблицу из 3674160 инвариантов, решение трёхмерного куба составляет максимум 11 ходов. Итак внежний гиперкуб собран.
Собрана внешняя гипергрань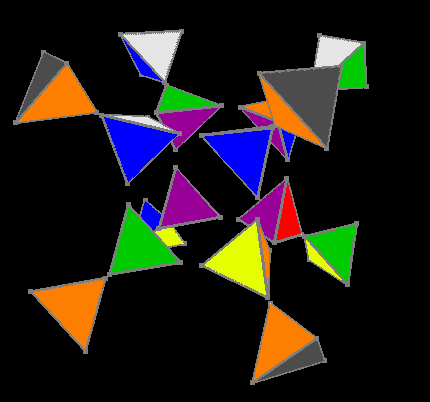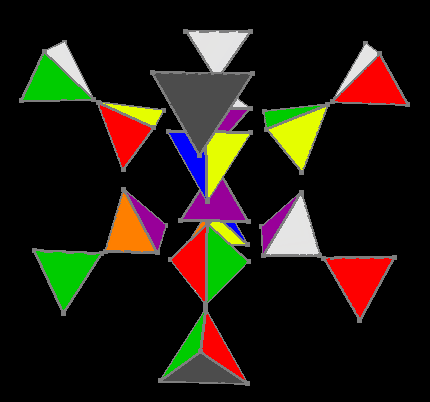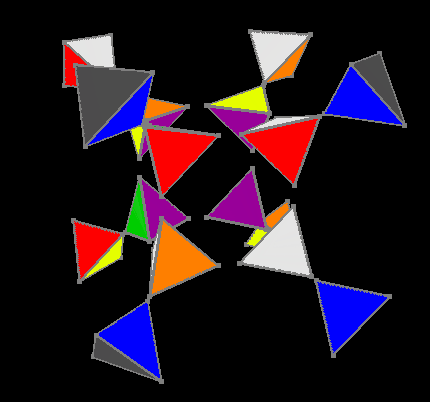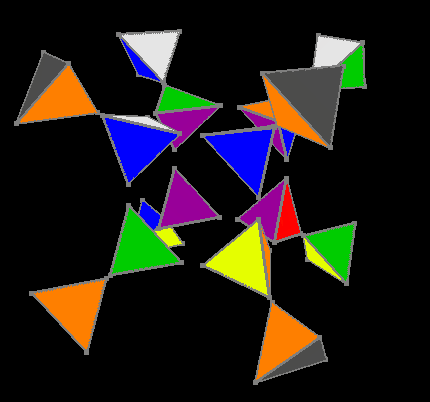
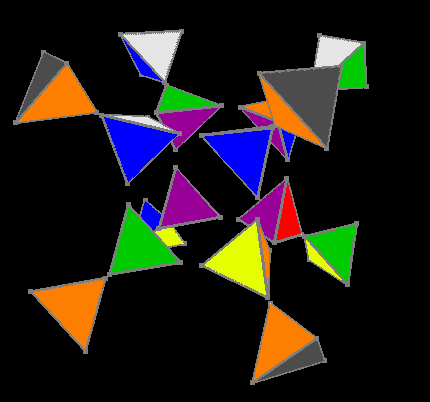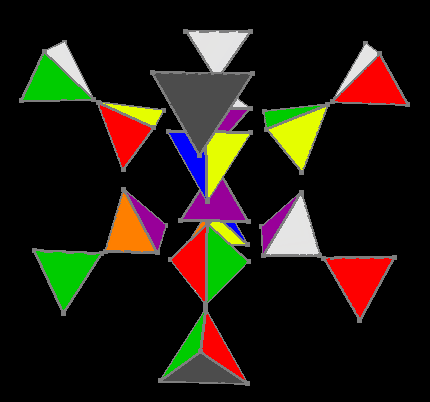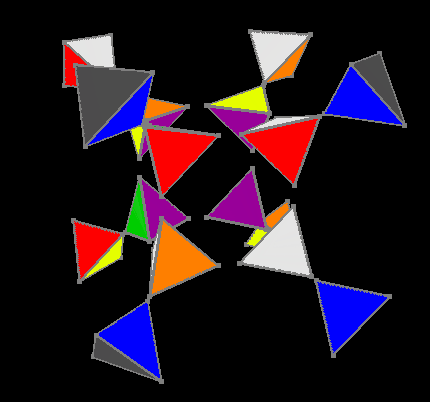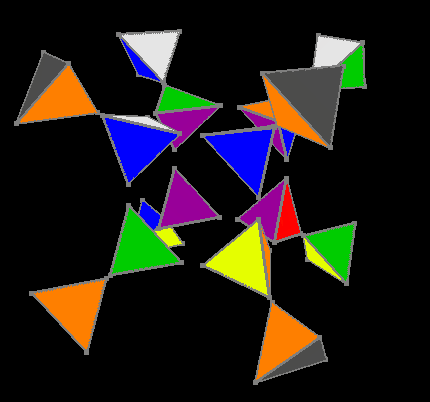
Для пятого этапа мы используем те же решения трёхмерного куба, за тем лишь исключением, что для каждого поворота какой-либо грани внутренний кубик поворачивается нужным боком относительно внешнего для каждого поворота, в результате внешняя, уже собранная, гипергрань вращает только свою правую часть и остаётся всегда почти собранной.
Пятый этап
У внешней грани вращается одна и та же правая сторона, а у внутреннюю мы проворачиваем всегда тем боком, который необходимо провернуть.

У внешней грани вращается одна и та же правая сторона, а у внутреннюю мы проворачиваем всегда тем боком, который необходимо провернуть.
То есть, используя таблицы, компьютер теперь обходился микросекундами на поиск, да вот только кэширование таблицы с HDD в оперативку отнимает несколько минут при инициализации программы. Ну и при наличии сразу трех таблиц с предрасчётами, алгоритм сборки уже не кажется сложным.
Вся сборка кубика

Только зарегистрированные пользователи могут участвовать в опросе. Войдите, пожалуйста.


jonywtf
интересно много ли людей способны представить 4-х мерное пространство и воспринимать его так же как 3-х мерное. Не особо задумываясь представлять 4-х мерные фигуры, вращать их, строить сечения, собирать из примитивов более сложные и т.д… все то что могут делать в голове люди с развитым 3д пространственным воображением… есть ли они вообще?
isden
Мозг человека эволюционно заточен под восприятие стереоизображения, составленного из 2-х плоских. Трехмерное и то получается посредством представления проекций этих двух плоскостей и разнообразных операций над ними (с привлечением предыдущего опыта). Ни о каком полноценном восприятии/представлении даже трехмерной сцены речи нет вообще.
kumbr_87
Ну почему же два, светотени вполне себе позволяют нам воспринимать объем и хоть картинка и является плоской но тем не менее яркость например на черно-белой картинке вполне можно принять за третье измерение аналогично тому как это реализовано, например, в Z-буфере в компьютерной графике.
isden
Ну это не полноценное трехмерное восприятие, скорее плоская картинка + карта глубины + личный опыт о форме/свойствах предметов.
Там есть видео ниже, там все достаточно прилично показано.
Полноценное — это, в двух словах, когда мы одним взглядом видим сразу все точки объекта.
kumbr_87
Так мы и видим, личный опыт о форме/свойствах предметов не при чем ведь не обязательно третье измерение (цвет) будет обозначать глубину как в графике, оно может показывать например температуру, силу ветра, давление и т. д., карта может быть не черно белой а изменяться от одного цвета к другому и т. д.
isden
Не, я больше про свойства перспективы, определение дальности и т.п., на основании чего строится модель сцены. Мозг ничего не знает о том, что может быть, и берет более часто используемую ассоциацию из своих закромов, и она, скорее всего, будет относиться именно к пространственной «навигации».
EvilPartisan
Ну да, особенно учесть, что это 4-ех мерное пространство является проекцией на трехмерное, а оно в свою очередь проецируется на двухмерную плоскость монитора.
m08pvv
Как говорилось в старом анекдоте, всё просто: представьте n-мерное пространство и положите n равным 4.
a_batyr
С этим были проблемы. В частности, когда я защищал эту дипломную, то я 30 минут объяснял почтенной комиссии почему это является 4-мерным объектом и как я его представляю в программе. Многие также думали, что я заблуждаюсь или обманываю. У некоторых 4 измерение автоматически ассоциируется со временем. А эту работу от начала до конца понял только я и мой научный руководитель, который мне также помогал разрабатывать алгоритм сборки.
Tazman
Когда-то давно написал 4-мерного пакмана. Игровое пространство представляло из себя несколько 3-мерных лабиринтов, которые существовали как бы в параллельных измерениях. Между такими лабиринтами существовали «коридоры». На самом деле пространство было абсолютно изотропным и не было никаких выделенных направлений, но объяснить людям, что это и есть 4-мерное пространство было очень сложно. Самой частой фразой, которую я слышал, было «4-ое измерение — это же время!?»
Randl
Ну мне помогает представить 4D объект протяженный во времени. Каждый 3D срез по четвертому измерению — это 3D объект в определенный момент времени.
a_batyr
Хм, теперь осталось лишь представить вектор перпендикулярный вектору времени и мы получаем пятое измерение. Что если время это комплексное число, а мы замечаем лишь действительную составляющую?
Mrrl
Если взять трёхмерную решётку трёхмерных сечений объекта, то легко работать и с шестимерным пространством.

Например, грани вот этого кубика шестимерны (показаны 7 граней и 5-мерные сечения еще шести):
Randl
Если концепцию четырёх- и более мерного пространства у меня ещё получается понять через аналогию 1D->2D->3D->4D, то с многомерным временем никак, потому что аналогий нет.
mwizard
Чтобы представить многомерное время, не покидая пределов уютного 3D-мирка, представьте плоскость, каждой точке которой соответствует куб, трехмерный срез. Для простоты можно даже представить, что плоскость замощена этими кубами стык в стык — или что она гладкая, но для любой точки можно получить «всплывающую подсказку», которая «призумит» соответствующий куб. Время, когда оно линейное (в 3D+1T варианте), это просто линия, проведенная по этой плоскости. Чтобы представить не все состояния сразу, а увидеть изменения, то можно ввести некоторый «курсор» — точку на плоскости, имеющую уравнение движения. Точка движется вдоль заданной линии, таким образом, в кубе «всплывающей подсказки» идет время, происходят изменения.
В пятимерном же варианте с двухмерным временем (3D+2T) «курсор» может двигаться не только вдоль некоторой линии, а вообще куда угодно в пределах плоскости — в том числе выписывать круги, ромашки, периодически пересекать свою траекторию и т.д.
Для трехмерного времени и трехмерного пространства, аналогично, представляем трехмерное «временнОе» пространство, каждой точке которого соответствует трехмерный куб, и у курсора текущего времени теперь три степени свободы.
Mrrl
Только это получается не время, а пространство вариантов. Похожее на то, что описывалось в последних книгах «Hitchhiker's Guide».
Randl
Но в чем тогда принципиальная разница между временем и пространством?
Mrrl
Исключительно в свойствах человеческой памяти. Мы «видим» только ту линию, по которой прошли, до точки, которая нам кажется «текущим моментом».
Randl
Тогда разницы между 3D+2T и 4D+1T никакой и смысла предпочитать первое нет
Mrrl
Верно, если вы можете свободно представить изменяющийся 4D объект.
michael_vostrikov
Есть вот такое неплохое изображение с визуализацией. При некоторой фантазии можно заметить, что кубы взаимно перпендикулярны.
Keyten
Кстати говоря, понимание 4 измерения как времени, в котором мы можем передвигаться, даёт вполне простое и интуитивное понимание 4-мерного пространства. Точнее, даже не времени, можно просто не пытаться проецировать четырёхмерное пространство на трёхмерное, которое проецируется на двухмерное, а рассматривать трёхмерные проекции четырёхмерного пространства: так вполне можно понять даже какой-нибудь сложный четырёхмерный объект и выше (да хоть двенадцати, если в уме уместить все проекции получится)…
В данном случае у нас кубик Рубика, меняя одну проекцию которого, мы меняем и остальные. Правда, представить алгоритм сборки такого человеку, не знакомому с алгоритмом сборки трёхмерного — очень страшно.
guai
Никогда не понимал, почему время — измерение. По пространственным измерениям можно ходить туда-сюда, а по времени только туда. Получается время — пол измерения.
Keyten
Потому что теория относительности.
Mrrl
По времени тоже можно ходить туда-сюда: в любом видеоплеере есть кнопочка «обратная перемотка». А то, что ваше сознание дрейфует в будущее с постоянной скоростью, да ещё и в памяти откладывается только прошлое — так это вопросы к сознанию.
a_batyr
Мне стало любопытно. Добавил опрос.
6opoDuJIo
Вероятно, все-таки речь идёт о представлении двухмерной проекции этих многомерных примитивов. Потому-что сами примитивы можно выразить в виде формулы при любом количестве пространственных измерений, не особо задумываясь о форме.
Mrrl
Это вопрос тренировки. Если некоторое время (несколько месяцев) активно решать задачи, связанные с 4D, то большую часть описанного делать можно. Хотя «не особо задумываясь» они это будут делать только в уже освоенной области, появление любого нового концепта требует дополнительных усилий по погружению.
Но стоит отвлечься на те же несколько месяцев — и эффект пропадает. И приходится начинать всё с начала.
Кстати, вот отличная игрушка, позволяющая освоить 4D «как оно есть»: www.urticator.net/blocks
Oxyd
Обычный тетрис есть, трёхмерный тоже. Возможен-ли четырёхмерный тетрис?
Mrrl
Вот моя неуклюжая поделка 10-летней давности: www.dropbox.com/s/m2bm2agfavochxc/t4.zip?dl=0
Визуализация полностью двумерная (исходно разрабатывалась ещё для MSX), показано дно стакана, вид сверху, в виде цветов клеточек. Сбоку видно, на каком уровне находится фигура. Фигуры сами не падают. Поддерживаются поля 3*3*3*16, 3*3*4*16, 3*4*4*16, 4*4*4*16, и наборы до 7 кубиков.
Игра довольно скучная, в варианте 3^3*16, 5 кубиков мне когда-то хватило терпения снять 7 рядов, в 4^3*16, 7 кубиков — один или два ряда.
anderston
Над эстетикой и визуализацией явно надо будет поработать, но в остальном просто замечательно, спасибо!
a_batyr
Ну, сударь, нет предела совершенству.
С визуализацией были явные проблемы в моей прежней работе, когда я делал алгоритм сборки трёхмерного куба. В итоге консольный интерфейс в стиле олимпиады по информатике «на входе дана последовательность ходов перемешивающих куб, на выходе последовательность собирающих ходов» никто не оценил. Я же считал визуализацию трёхмерного куба излишней надстройкой и фокусировал всё внимание на разработке алгоритма. А вот когда я перешёл к работе с 4-мерным кубиком, то мне без визуализации было туго и первым шагом к разработке алгоритма стало «вообразить и изобразить чтобы можно было вообразить», такая вот рекурсия. Кстати, анимация тессеракта из википедии стала фундаментом для воображения движения моего гиперкуба.
willson
а как по мне, так визуализация шикарна :) хоть стало понятно, как оно работает. Я бы поиграл в такую головоломку.
a_batyr
Спасибо. Насчёт поиграть, будет сложновато такой собирать.
Первый вариант — придётся пользоваться моими таблицами ориентирования серого и пурпурного цветов (которые описывают 256 и 65536 комбинаций).
Второй вариант — разработать свою методику сборки этой системы.
Самый ужас состоит в том, что вместо милых взору FRUR'U'F' придётся различать 192 поворота на каждый ход.
Если без алгоритма сборки, то в принципе не мудрено сделать приложение под андроид с визуализацией описанной концепции.
anderston
Такая возможность есть=)
play.google.com/store/apps/details?id=com.superliminal.magiccube4d
a_batyr
Что-то у них не отображена восьмая гипергрань Kata.
Но такая визуализация имеет преимущество перед моей в том, что они могут отображать 3х3х3х3 головоломку.
anderston
Пожелание скорее в плане эстетики, не более того, ваша статья очень хорошая=) Например, оттенки цветов я бы лично просто взял отсюда: flatuicolors.com Это красивее смотрится.
a_batyr
Ваша ссылка не открылась. Эстетичность нашёл тут flatuicolors.co
Aingis
Реквестирую скринсейвер! С такой анимацией как в конце статьи («Вся сборка кубика») он будет выглядеть шикарно!
a_batyr
Сейчас поготовлю на ютуб 1080p видео. А там уже любой fair use на любой вкус.
a_batyr
Добавил видео в конце статьи (ютуб сжал в 720p). Если будут проблемы с просмотром, сообщайте в личку. У меня, например, firefox сегодня не отображает ютуб, в хроме и старой опере всё нормально.
a_batyr
А если вы имели ввиду программный скринсейвер постоянно генерирующий новые решения, то такой будет слишком ресурсоёмким. К тому же программа не до конца отлажена и порой банально вываливается с ошибкой.
ripatti
Я попробую написать скринсейвер как-нибудь на выходных
a_batyr
Распишу для начала исходные данные:
Входные файлы с таблицами весят «61,485,632 bytes in 3 files», инициализация таблиц для быстрого поиска решений при запуске программы занимает не менее трёх минут на моей машине. Для скринсейвера эти варианты не подходят.
Зато подходит такое решение, я могу запустить программу и нагенерировать несколько десятков, а может и пару сотен scramble-solve комбинаций. Ходы сохраняются в текстовике. Используя заранее расчитанные комбинации можно крутить скринсейверы.
ripatti
Я так понял, что бОльшую часть занимает таблица для сборки 2х2х2. Так вот, кубик рубика 2х2х2 решается без всяких таблиц при помощи идеи meet in the middle за 0.2 секунды (эту задачу я решал тут acm.mipt.ru/judge/problems.pl?problem=041).
А с остальным вроде же проблем нет? Или я что-то пропустил?
a_batyr
Да, верно, мои дополнительные таблицы занимают всего-то 5%. Ваша идея значительно ускорит инициализацию. Но самый решающий фактор это
То есть даже реализовав meet in the middle придётся ещё изрядно поработать над кодом, чтобы банально не ловить crash. Я буду восхищён, если вы реализуете «скринсейвер как-нибудь на выходных».
ripatti
Вы недооцениваете мою мощь (с)
Хотя, на самом деле не обещаю, что управлюсь за одни выходные, может быть понадобится чуть больше времени. Просто после прочтения статьи захотелось что-нибудь программно повращать, давно я таким не занимался (тем более в 4х-мерном пространстве). Поразвлекаюсь, в общем. Ну и посмотрим что из этого выйдет.
maeln0r
А сможете статью про это написать? Было бы очень интересно почитать.
ripatti
Если что путное выйдет и получится достаточно материала, не повторяющего данную статью — напишу.
nemilya
Мне кажется, чтобы понять 4х мерное в контексте 3х-мерного — надо найти принцип, как «понимать» 3х мерное из 2х мерного (при условии, что мы-то знаем как выглядит 3х мерное:)
BalinTomsk
принцип простой — вы легко попадаете в 2-х мерный круг пальцем в 3-х мерном пространстве.
Точно также можно попасть в 3-х мерный сейф из 4-х мерного
Sild
То, что вы сделали, очень круто и красиво. И в плане визуализации, и в плане алгоритма.
ArXen42
Захотелось стать паранидом, чтобы понять священную n-мерность.
anderston
Возможно это видео вас утешит=)
sergey_dobrodey
Напоминло рассказ «Феномен Архимеда» читать
Beyondtheclouds
Была анимешная игрушка с близкими объяснениями) ever17 :)
Mrrl
Хороший вариант. Недостаток по сравнению с версией ( superliminal.com/cube/cube.htm ) — что там мы видим (при маленьком размере стикеров) грани гиперкуба во всём объёме, а у вас есть такая неприятность, как невидимые грани тетраэдров. При сборке будет труднее ориентироваться. Ну, и интересно, как вы обобщите это представление на N^4 и на другие многогранники.

Впрочем, если добавить призмы и «монетки» (для трёхцветных и двухцветных кубиков), то куб N^4 показать будет можно. Надо будет только придумать, как лучше всего задавать повороты граней для команд пользователей.
Для некоторых головоломок такой режим (слипшиеся грани, маленькие кубики) может быть даже удобнее, чем маленькие грани, плавающие в пустоте. Например, одну из своих головоломок мне удобнее было собирать в таком режиме:
(у тетраэдров здесь окрашены вершины, а не грани).
Что отвечать на опрос, не знаю. Понятно не стало, потому что было понятно изначально :)
a_batyr
Это примерно как невидимая задняя и нижняя грани обычного кубика. Боюсь, видеть все грани одновременно избыточно (кстати, ваша картинка прекрастно иллюстрирует избыточность), мозг хорошо кеширует неободимую информацию и для лучшего восприятия совершенно естественно прятать лишнее.
Mrrl
Кстати, кубик 3*3*3*3 собрали уже 214 человек.
Mrrl
Попробовал собрать кубик 2^4. Получилось довольно медленно — 21 минута. Основной проблемой оказалось то, что у граней нет центров — а я забыл записать, какие грани изначально были противоположными. Поэтому когда понадобилось указать место, куда ставить очередной кубик, принадлежащий почти несобранной грани, мозг озадачился — зацепиться было не за что. В этом смысле кубик даже сложнее, чем 3^4.
Turilion
Блин, вот я даже зная алгоритм сборки трехмерного куба и предсьавляя четырёхмерное пространство не смогу представить, как перенести алгоритм туда, А тем более спроецировать процесс сборки на плоскость. Никак не могу уложить вголове принцип по которому вращаются грани кубика в четырёхмерно пространстве. Ну точное предствить то могу, не пойму как это отразить на плоскости.
a_batyr
Алгоритм сборки трёхмерного применяется только с момента, когда ориентированы гиперграни Ana-Kata (purple-gray), после чего остаётся только применить сборку 2х2х2 не смешивая внутренней и внешней граней, а вращая только правую/левую, верхнюю/нижнюю, переднюю/заднюю. Как только мы сориентировали gray-purple, задача сведена к трёхмерной.