В 2015 году математик Ласло Бабай представил свой более эффективный алгоритм, решающий задачу изоморфизма графов (Graph Isomorphism, GI) за квазиполиномиальное время. На Хабре даже есть статья, освещающая это событие. Однако в дальнейшем сам учёный признал некоторую ошибочность своего подхода, что всё равно не повлияло на отношение большинства математиков к его открытию, поскольку даже получившийся вариант, решающий задачу за субэкспоненциальное время, оказался эффективнее существующих алгоритмов. Тем не менее учёный не остановился на этом и обнаружил ошибку. Опубликованные исправления алгоритма всё-таки привели к решению задачи изоморфизма за квазиполиномиальное время.

Проблема изоморфизма графов требует алгоритмов, которые могут определить, являются ли два графа структурно идентичными. На протяжении десятилетий эта задача занимала особый статус как одна из немногих естественно возникающих задач, уровень сложности которых трудно определить. Многие годы исследователи пытались выяснить, к чему она относится. Даже сейчас неизвестно, к какому классу относится задача, а абстрактно задачу рассматривают как нечто среднее — сложнее, чем P, но легче NP. Задачу из теории графов можно обобщить до общей проблемы изоморфизма, в смежных областях математики существуют идентичные задачи, например изоморфизм конечных групп.

Итак, общая задача определения идентичности может показаться достаточно тривиальной для человека, и в большинстве повседневных случаев достаточно беглого взгляда, чтобы вынести верное суждение. В информатике это гораздо более сложный вопрос, затрагивающий саму суть возможностей компьютеров. Проблема открытая, и её решение сильно зависит от формализации сравниваемых объектов и используемых алгоритмов. По сути, до открытия Бабая самым быстрым был обычный перебор. Однако в прошлом году был представлен новый, ещё более быстрый алгоритм для смежной задачи из теории групп. Исследование продвинуло чуть дальше прояснение базовой вычислительной сложности, связанной со сравнением объектов. В идеале предложенный алгоритм может работать не только с группами, но и с другими типами изоморфизма. Хотя ещё нет убедительного доказательства данного утверждения, многие специалисты положительно оценивают его вероятность.

Для точной оценки «одинаковости» объектов, прежде всего, необходимо выбрать критерии этой оценки, например, могут ли две строки чисел считаться одинаковыми, если они просто содержат одни и те же цифры, или нет, т. е. что вообще признавать за «одинаковость». В математике для этого и ввели достаточно точный термин «изоморфизм». Два объекта изоморфны друг другу, если они содержат одни и те же элементы, находящиеся в одинаковых структурных отношениях между собой.

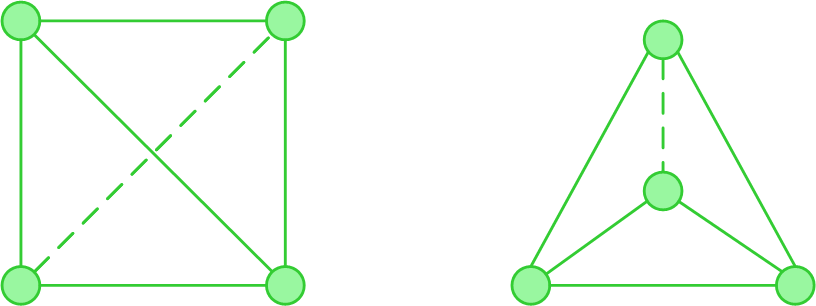
Два графа изоморфны, если можно сопоставить вершины одного графа с вершинами другого так, что вершины, соединенные ребром в первом графе, также соединены ребром и во втором. Изоморфные графы на первый взгляд могут выглядеть по-разному, но обладают общей базовой структурой.

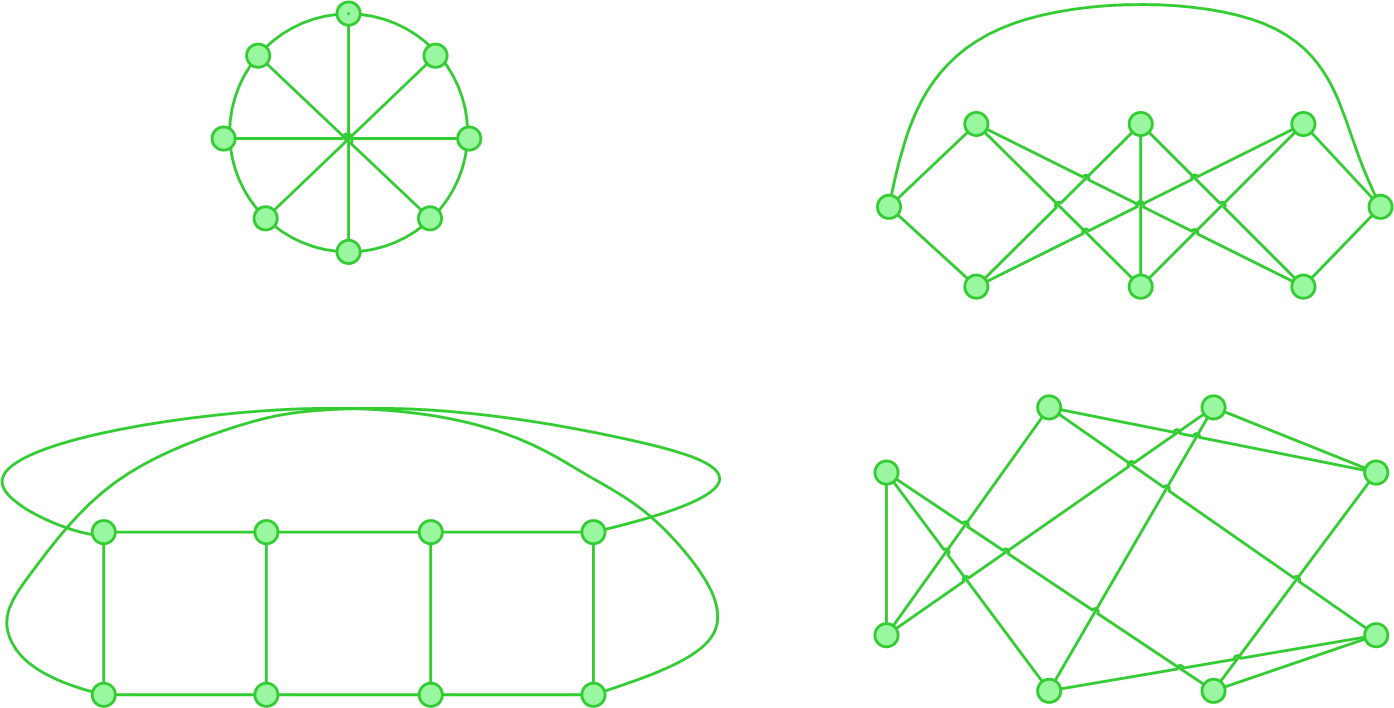
Группы более абстрактны, чем графы, и их изоморфизм не так просто увидеть невооружённым глазом. Две группы изоморфны, если можно сопоставить каждый элемент одной группы с элементом другой так, что результат операции над двумя элементами в первой группе согласуется с результатом операции над эквивалентными значениями этих элементов во второй группе.

Простой пример двух изоморфных групп, каждая из которых состоит из двух элементов на рисунке ниже. Первая группа состоит из цифр «0» и «1», а вторая группа — из переменных X и Y. Обе группы содержат операцию объединения элементов группы определённым образом.

Группы изоморфны, потому что «0» сопоставляется с X, «1» — с Y, а структурные отношения, возникающие при объединении элементов, идентичны в обеих группах.

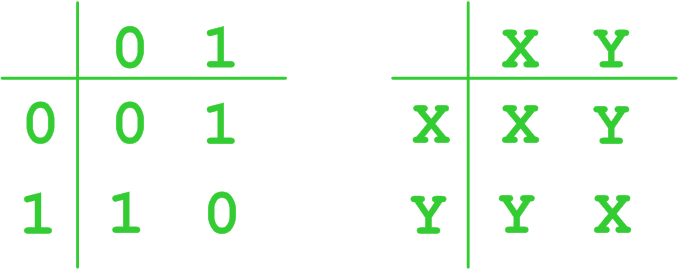
Изоморфизм — важное математическое понятие, позволяющее абстрагироваться от поверхностных отличий. Современные исследователи находятся в поисках более эффективных и быстрых алгоритмов, выявляющих изоморфизм объектов, что на самом деле является очень непростой задачей. Скорость алгоритма зависит от того, как время его выполнения изменяется в зависимости от размера объектов, над которыми он работает. Например, имеется две пары групп. В одной паре каждая группа содержит по пять элементов, в другой — по десять. Как определить насколько больше времени потребуется конкретному алгоритму для определения изоморфизма? В два, 5² или 2⁵ раз больше?

Эти варианты соответствуют широко известным классификациям алгоритмической скорости. В первом случае алгоритм выполняется за линейное время (что означает, что он работает в два раза дольше), во втором — полиномиальное (5²) и в третьем — экспоненциальное время (2⁵).

Большинство известных вычислительных задач явно относятся к какой-либо категории алгоритмической скорости, но есть исключения из правил. Как раз к таким исключениям относится задача определения изоморфизма, что делает её привлекательной для детального изучения.

Ещё в 1970-х годах Роберт Тарьян понял, что существуют алгоритмы, которые могут выявить изоморфизм двух групп за время n^{(log n)}, где n — количество элементов. Такие алгоритмы стали называть алгоритмами квазиполиномиального времени, и в связанной иерархии рабочих циклов они лучше, чем экспоненциальное время 2ⁿ, но хуже полиномиального времени n². Именно такой алгоритм разработал Бабай, и пока это был лучший результат за половину века исследований. В то время проблема изоморфизма групп изучалась более интенсивно, чем изоморфизм графов, в отличие от сегодняшних реалий, что, в принципе, не удивительно, учитывая современные приложения теории графов. Некоторое время изучение изоморфизма групп вообще застопорилось.

Как я уже писал выше, задачи изоморфизма в теории графов и групп имеют более глубокую связь, чем сходство названий, и одна проблема может сводиться к другой (т. е. любой алгоритм, способный решить задачу на графах, может решить и задачу с группами за точно такое же время). Интересна лишь некоторая ассиметрия — пока обратная сводимость не доказана.

Сегодня интерес к изучению изоморфизма групп возобновился. Как обычно бывает в случаях продолжительного застоя в какой-либо сфере, для выхода из тупика необходимы оригинальные идеи. В исследовании доцента кафедры Computer Science Иллинойского университета Сяоруи Сана (Xiaorui Sun) содержится несколько таких идей. Прежде всего, учёный сконцентрировался на более простых алгебраических структурах, чем общие группы. В таких группах произведение двух элементов является другим элементом группы, и произведение остаётся одним и тем же, независимо от порядка умножения. Подобное допущение предоставляет важные следствия для общей проблемы группового изоморфизма. Так как группы имеют простую структуру, их сравнение должно быть не очень сложным, однако до недавнего времени исследователи так и не придумали, как ускорить алгоритмы сравнения. Пока это было недостижимо в этом частном случае, невозможно было даже думать об улучшении общего вопроса изоморфизма групп.

Проблема изоморфизма групп состоит в том, чтобы определить, являются ли две группы, заданные их таблицами Кэли, изоморфными. Практические аспекты применения этой задачи и её вариантов тесно связаны с криптографией, вычислительной теорией групп и теорией алгебраической сложности. Кроме того, после публикации и доработки алгоритма квазиполиномиального времени для изоморфизма графов, описанного выше, задача определения идентичности групп стала узким местом для обобщённой теории изоморфизма, поскольку изоморфизм групп достаточно легко сводится к изоморфизму графов.

Для исследования Сан переключился с групп на матрицы. Это стало возможным благодаря соответствию Бэра, которое превращает проблему изоморфизма групп в совершенно схожую проблему с матрицами. В частности, он работал с матричными пространствами, которые представляют собой наборы матриц с определённым свойством: (линейная) комбинация любых двух матриц в пространстве равняется другой матрице в пространстве, что очень похоже на группы. Поэтому вместо того, чтобы пытаться понять, когда две группы изоморфны, Сан старался вычислить изометрию матричных пространств.

Подобный подход применялся и ранее, однако впервые был введён дополнительный элегантный этап: разбиение матричного пространства на две части. Одна часть — ядро пространства, в котором все матрицы простые. Другая часть — это пространство, окружающее ядро, и в нём все матрицы более сложные. Такой ход аналогичен разбиению группы на подгруппы, содержащие только некоторые из общих элементов.

К каждой из частей применялись разные алгоритмические методы. Так как ядро имеет простую структуру, его анализ производится в первую очередь. Внешний слой более сложен, поэтому пока очевидно быстрого способа сравнения не существует. Снимаю шляпу, решение лежало на поверхности, но никто ранее его не применял, по крайней мере, мне об этом неизвестно.

Сущность метода похожа на одну из стратегий решения судоку, когда первым делом по квадратам ищутся ячейки, очевидные для заполнения. То есть некоторые квадраты, потенциальные значения пустых ячеек которых заполняются тривиальным исключением и логикой (в нашей ситуации — ядро матричного пространства), что позволяет вам быстро их заполнить. Оставшиеся квадраты с большей вариативностью заполнения обычно заполняются методом простого перебора (внешний слой матричного пространства). Даже если внешний слой больше ядра, всё равно общее время решения головоломки меньше, чем простой перебор по всему пространству решений. Простой алгоритм группового изоморфизма по Тарьяну, выбирает набор образующих в одной из групп и проверяет для всех возможных образов набора образующих в другой группе, расширяется ли частичное соответствие до изоморфизма. Поскольку каждая группа порядка n имеет порождающий набор размером не более log2n, этот алгоритм приводит к времени выполнения n^log2n+O(1). Текущий наиболее известный алгоритм для решения проблемы группового изоморфизма выполняется за n^{(1/4+ o(1)) log2n}.

Предложенный подход с разделением и комбинациями алгоритмических методов позволяет выявить изоморфизм за время меньшее, чем требовалось для решения ранее известными алгоритмами. Несмотря на это, такой результат всё ещё не позволяет однозначно определить принадлежность обобщённой задачи к какому-то конкретному классу вычислимости, однако по времени решения он также находится между экспоненциальным и полиномиальным временем, но немного ближе к полиномиальному. В конце концов, данный алгоритм даёт надежду на возможность его успешного использования как для обобщённых групп, так и для других типов подобных задач сравнения.

Для доказательства эффективности алгоритма, как я уже писал выше, Сан использует соответствие Бэра, которое сводит проблему группового изоморфизма для p-групп класса 2 и степени p к проблеме проверки изометрии кососимметричных матричных пространств. Такие матрицы относятся к специальным классам квадратных матриц. Квадратная матрица A является кососимметричной матрицей, если A^T = -A, где A^T — транспонированная матрица. В задаче проверки изометрии для кососимметричных матричных пространств вход состоит из линейных базисов двух кососимметричных матричных пространств A и B. Задача состоит в том, чтобы решить, существует ли изометрия S из в , т. е. обратимая матрица S такая, что SS^T =, где SS^T — линейная оболочка матриц SAS^T для всех матриц A ∈. 

Проблема группового изоморфизма изучалась для групп различных классов. Алгоритмы полиномиального времени разработаны для абелевых групп, групп, образованных полупрямыми произведениями абелевой и циклической группы, групп с нормальными холловскими подгруппами и других. Последние исследования показали, что проблема группового изоморфизма может быть решена почти за линейное время для большинства вариантов.

Зачем всё это нужно?

Практические приложения теории изоморфизма охватывают широкий спектр областей, от химии до компьютерного зрения. Тесно связаны проблемы обнаружения симметрий графов и общих комбинаторных структур. Опять же, у этого есть много областей применения, например, комбинаторная оптимизация, создание комбинаторных структур и вычисление нормальных форм. Начиная с 1950-х годов, изоморфизм графов как вычислительная проблема впервые появляется в литературе по химической документации как проблема сопоставления молекулярного графа с базой данных таких графов. Далее она неоднократно упоминалась как открытая проблема, например, в фундаментальной статье Карпа о NP-полноте. С тех пор определение точной вычислительной сложности графического изоморфизма стало считаться серьёзной открытой проблемой теоретической информатики. По мере того как вопрос о том, является ли изоморфизм NP-полным, приобретал все большее значение, стало понятно, что он имеет аспекты, отличающие его от большинства других NP-полных задач. В частности, подсчитать количество изоморфизмов между двумя графами не сложнее, чем решить, существует ли он вообще.

На начало 1980-х пришлась первая волна существенного прогресса, и были представлены методы теории групп. Примерно в то же время Маккей разработал инструмент для определения изоморфизма Nauty.

В середине 1980-х годов была обнаружена еще одна увлекательная грань сложности GI. С тех пор никакого реального прогресса в этом направлении не наблюдалось. Пока в 2015 году Бабай не опубликовал свой квазиполиномиальный алгоритм.

Чтобы установить, что два графа изоморфны, можно пытаться найти его, а можно наоборот установить обратное. Например, посчитать вершины, рёбра и треугольники в обоих графах, если какой-либо из этих показателей отличается, графы не изоморфны. Для решения этой задачи существуют описанные комбинаторные алгоритмы. Например, Вайсфейлера-Лемана (WL) или уточнение цвета (Color refinement, CR). Алгоритм Вайсфейлера-Лемана обеспечивает систематический подход к эффективному созданию таких сертификатов неизоморфизма. Собственно, это целое семейство алгоритмов, параметризованных целым положительным числом (размерностью, k).

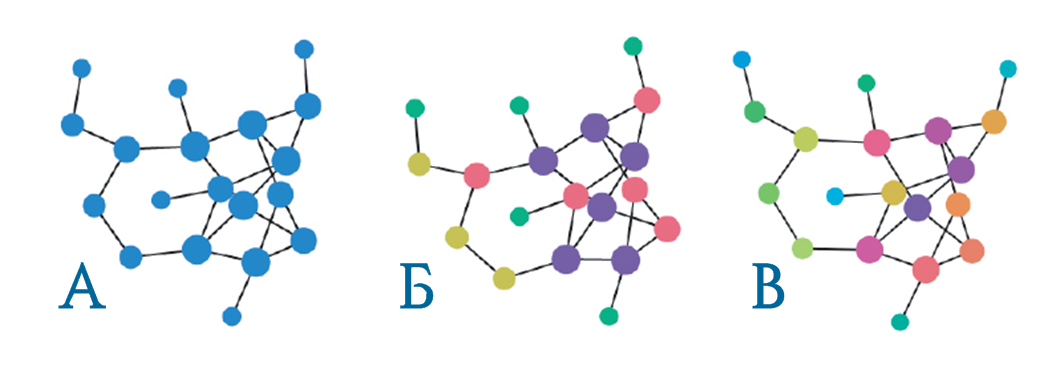
Уточнение цвета иногда называют наивной классификацией вершин. Это одна из самых базовых идей проверки изоморфизма графов, которая несколько раз изобреталась заново. Самая старая известная опубликованная версия датируется 1965 годом. Уточнение цвета — важная подпрограмма почти всех практических инструментов изоморфизма графов.

Фактически используемые цвета не имеют значения, важно лишь разделение вершин на цветовые классы. Окончательная раскраска обладает тем свойством, что любые две вершины одного цвета имеют одинаковое количество соседей в каждом цветовом классе.

Раскраска, вычисляемая алгоритмом, инвариантна к изоморфизму, что означает, что если мы запустим его на двух изоморфных графах, результирующие цветные графы все равно будут изоморфными и, в частности, будут иметь одинаковое количество узлов каждого цвета. Таким образом, если мы запустим алгоритм на двух графах и обнаружим, что они имеют разное количество вершин определенного цвета, мы получим объективный сертификат неизоморфизма. В таком случае говорят, что CR различает два графа.

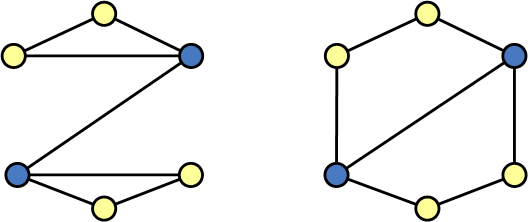
К сожалению, уточнение цвета не различает все неизоморфные графы. На рисунке ниже показан простой пример. Но, что примечательно, уточнение цвета различает почти все графы в вероятностном смысле. Это, вместе с его эффективностью, делает уточнение цвета очень полезным в качестве простейшей подпрограммы практических инструментов определения изоморфизма.

Также уточнение цвета очень похоже на другие алгоритмы разбиения, в частности на стандартный алгоритм минимизации детерминированных конечных автоматов. Заимствуя идеи из алгоритма минимизации Хопкрофта, CR можно реализовать за время O((n+m)log n), где n — количество вершин, а m — количество рёбер входного графа. Таким образом, уточнение цвета действительно очень эффективно.

Уточнение цвета не является стопроцентным тестом на изоморфизм: оно не позволяет различить некоторые чрезвычайно простые неизоморфные графы. Вместо вершин k-WL раскрашивает k-наборы вершин графа. Изначально каждый набор k «раскрашивается» типом изоморфизма индуцируемого им подграфа. Затем на этапах уточнения информация о цвете распространяется между «соседними» кортежами, которые отличаются только одной координатой. При реализации с использованием тех же идей, что и для уточнения цвета, k-WL работает за время O(nk + 1 log n).

Многомерный WL очень мощный. Действительно, очень нетривиально найти неизоморфные графы, которые не различаются 3-WL. По этому поводу даже потребовалось отдельное исследование, чтобы доказать, что для каждого k существуют неизоморфные графы, которые не различаются k-WL. Действительно, эти графы, известные как графы CFI (Cai-Furer-Immerman), имеют размер O(k) и являются 3-регулярными.

Оказывается, что многие классы естественных графов не допускают построения CFI-графа, а низкоразмерный WL является тестом полного изоморфизма. В частности, для всех классов графов C, которые исключают какой-либо фиксированный граф в качестве минора, существует константа k такая, что k-WL различает все неизоморфные графы.

Алгоритм Вейсфейлера-Лемана удивительно надежен. Он не только включает в себя большинство комбинаторных идей для проверки изоморфизма графов, но также имеет естественную характеристику с точки зрения логики. Интересно, что он также соответствует естественному тесту на изоморфизм, основанному на линейном программировании, и включает в себя различные подходы к GI, основанные на методах алгебраического и математического программирования.

Хотя большинство разработанных алгоритмов изоморфизма относятся к типу WL, это не относится к теоретико-групповому подходу. Первое применение алгоритмической теории групп к проверке изоморфизма было развито Бабаем в его работе. 

На практике даже 2-мерный алгоритм Вейсфейлера-Лемана является излишним, не говоря уже о каком-либо варианте увеличения размерности, как в алгоритме Бабая. Текущие программы определения изоморфизма реализуют CR, то есть вообще одномерную версию. Как уже упоминалось, этого уже достаточно почти для всех графов. Если этого оказывается недостаточно, алгоритмы идут по пути ветвления, используя концепцию индивидуализации.

В частности, парадигма индивидуализации-уточнения, принятая практически всеми современными инструментами конкурентного изоморфизма, одна за другой искусственно присваивает разные цвета всем вершинам в цветовом классе. Это нарушает симметрию, и впоследствии можно снова применить уточнение цвета для получения более точного разделения вершин. Прикладные программы используют различные методы сокращения для повышения их производительности, и фактически каждая вычисляет каноническую форму, что также решает проблему изоморфизма. Впервые этот очень практичный метод был применен Маккеем в Nauty. В настоящее время в свободном доступе находятся различные достаточно эффективные программы (Bliss, Conauto, Nauty, Saucy, Traces).

Определение изоморфизма графов на практике может использоваться для поиска симметрии комбинаторных объектов, и поэтому находит множество приложений в разных областях. В контексте оптимизации, например, при решении SAT, симметрии используются для сужения пространства поиска, поскольку части, эквивалентные симметриям, нужно исследовать только один раз. Альтернативным способом использования симметрий является добавление ограничений, нарушающих симметрию, к исходным входным данным, что значительно повышает производительность приложений.

Изоморфизм используется для формирования канонической маркировки графов в системах хранения структурированных графов в базах данных. Например, графов молекул в химических базах.

Алгоритм Бабая с квазиполиномиальным временем стал прорывом в решении одной из старейших и лучше всего изученных алгоритмических задач. Несомненно, этот алгоритм и лежащая в его основе математическая структура считаются одним из самых важных вкладов в теоретическую информатику за последнее время и ещё до конца не определены границы его потенциального приложения.

Текущие проблемы исследователей сосредоточены на задаче изоморфизма групп, одного из основных препятствий для ещё более быстрых тестов изоморфизма графов. С практической стороны новые приложения в таких областях, как машинное обучение, требуют лучшего понимания версий приблизительного определения изоморфизма и подобия между графами. Тем не менее вопрос о том, разрешим ли изоморфизм графов за полиномиальное время, остаётся открытым, и стоит ожидать дальнейших глубоких и захватывающих открытий на этом поприще до тех пор, пока этот вопрос не будет окончательно приземлён.

Одно из самых важных и интересных для меня приложений проблем изоморфизма связано с криптографией. Современная криптография стала такой, как есть, благодаря смене основополагающих принципов. Алгоритмы шифрования стали основываться на конкретных алгебраических задачах, таких как факторизация и дискретный логарифм. Одними из первых изоморфизм графов предложили использовать в криптографии Брассард и Юнг. Они предложили подход к использованию группового действия для создания односторонней функции. Однако поиск конкретных групповых действий для реализации такого подхода оказывается непростой задачей, особенно с учетом потенциальных угроз со стороны злоумышленников, способных к квантовым вычислениям. Для изоморфизма графов существуют эффективные эвристические решатели, которые я упоминал выше, а также эффективные алгоритмы усреднения, не говоря уж об алгоритмах квазиполиномиального времени. Знаменитая работа Шора решает задачи дискретного логарифмирования и факторизации за полиномиальное время на квантовом компьютере, что гипотетически ломает подавляющее большинство криптографических реализаций с открытым ключом. 

Сейчас прилагаются значительные усилия по разработке постквантовой криптографии, способной противостоять квантовым атакам. Помимо изогении, популярны предложения, основанные на дискретных решётках и многомерных уравнениях. Хотя до триумфального выхода на сцену квантовых компьютеров ещё есть время, большинство исследований в этой области направлены на поиск и разработку инструментов, которые могут служить квантово-безопасными решениями.

P.S. Интересные статьи на Хабре по теме:

— Big O

— Знай сложности алгоритмов

— Постквантовая реинкарнация алгоритма Диффи-Хеллмана

НЛО прилетело и оставило здесь промокод для читателей нашего блога:
-15% на заказ любого VDS (кроме тарифа Прогрев) — HABRFIRSTVDS.