Статья-туториал для тех, кто хочет узнать, как из заголовка получается «6» методом рекурсивного спуска. Начнём с самого простого и дойдём до вычисления -1.82 или около того из строки -2.1+ .355 / (cos(pi % 3) + sin(0.311)).
Конечно, этот метод неоднократно описан на Хабре и зачитан каждому айтишному первокурснику. В своей версии я хочу изложить его очень просто и подробно, с позиции элементарной практики на JavaScript. Ссылки на рабочий код — в самом низу.
«2»
Разберём невыносимо простой пример: на входе у нас строка с двойкой, а на выходе должно быть число 2. Разумеется, тут достаточно вызова функции parseInt, но давайте напишем так, чтобы было от чего отталкиваться на следующих уровнях.
function calc(tokens) { // ['2']
let result = parseInt(tokens.shift()); // ['2'] → '2' → 2
if (tokens.length) throw new Error('expected eof'); // [empty array]
return result; // 2
}
console.log(calc('2'.split('')) === 2); // trueЗачем мы делим строку на символы, да ещё когда она состоит из всего одного? На самом деле нам нужны не отдельные символы, а элементы выражения, которые называются токенами. Числа — это один вид токенов, операторы +, -, *, / — другой (причём каждый оператор может быть отдельным видом), скобки — третий и т.д. Но для начала пускай каждый токен будет символом, ведь так выражение гораздо проще разрезать на токены (токенизировать): достаточно вызвать .split('').
Кроме того, тут появляется понятие EOF (end of file) и вводится правило, по которому после выражения сразу должен идти конец файла/ввода. Представьте, что на вход подаётся строка 2#. Без проверки EOF мы бы так и вывели двойку, проигнорировав #, а такие вольности недопустимы. Выражение 2+2 точно так же должно сбить с толку наш парсер на этом этапе.
Кстати, в JavaScript метод shift() выдаёт первый элемент и удаляет его из массива. Этим будем пользоваться, чтобы идти по токенам. Иногда будем проверять токен, прежде чем удалить его, типа if (tokens[0] === '+') { tokens.shift(); ... }.
«2+2»
Пойдём дальше по выражению дальше и, встречая + либо - , будем решать, что делать со следующей за ними цифрой — добавить или вычесть из накопленного результата.
function expr(tokens) { // ['2', '+', '3', '-', '4']
let result = parseInt(tokens.shift());
// NEW
while (true) {
if (tokens[0] === '+') {
tokens.shift(); // throw away the '+'
result += parseInt(tokens.shift());
}
else if (tokens[0] === '-') {
tokens.shift(); // throw away the '-'
result -= parseInt(tokens.shift());
}
else break;
}
return result;
}
function calc(tokens) { // ['2', '+', '3', '-', '4']
let result = expr(tokens);
if (tokens.length) throw new Error('expected eof');
return result;
}
console.log(calc('2+2'.split('')) === 4); // true
console.log(calc('2+3-4'.split('')) === 1); // trueКроме того, мы вынесли часть алгоритма в отдельную функцию expr, хоть и можно было продолжать писать всё в calc. Такое разделение пригодится нам позже.
Давайте подсунем нашему калькулярсеру какую-нибудь ерунду, убедимся, что он не выводит случайный числовой результат, и двинемся дальше.
console.log(calc('+'.split(''))); // NaN
console.log(calc('+1'.split(''))); // Error: expected eofПока сойдёт. Одинокий плюс никакого числа не представляет, а поддержку +1 (унарный плюс) мы добавим позже вместе с унарным минусом.
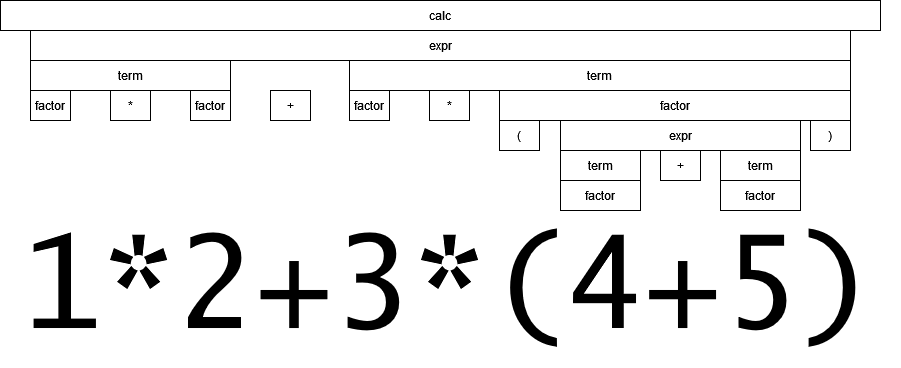
«2+2×2»
Естественно, тут подвох в приоритете операций умножения/деления над операциями сложения/вычитания, поэтому нельзя просто добавить блок else if (tokens[0] === '*') {...} вслед за плюсом и минусом, ведь тогда получится 8. Здесь-то на помощь и приходит рекурсия языка программирования, на котором мы пишем этот калькулятор. В JavaScript рекурсия есть, и потому этот метод легко реализуется. Но есть условно современные языки без поддержки рекурсии — например, structured text в IEC 61 131–3, на котором программируются контроллеры в среде промышленной автоматики.
Оставим двойки для красивого заголовка, и, чтобы проще было следить за руками, возьмём пример 3+4×5. Да, говоря обывательским языком, нам нужно сначала посчитать 4×5 и уже потом складывать это с тройкой. Но можно переформулировать и более удобным для программирования образом: сложить тройку с тем, что главнее сложения. А значит, можно как обычно начать считывать тройку, потом + за ней, а потом «отвлечься» на вычисление 4×5, результат которого и сложить с ранее замеченной тройкой. Вот на этом «отвлечься» и строится принцип рекурсивного спуска. Давайте оформим «отвлечься» новой функцией term, которую реализуем точно так же, как сделана expr выше. Ну а в expr будем вызывать term там, где прежде считывали цифры.
function term(tokens) { // like old `expr` but * and /
let result = parseInt(tokens.shift());
while (true) {
if (tokens[0] === '*') {
tokens.shift(); // throw away the '*'
result *= parseInt(tokens.shift());
}
else if (tokens[0] === '/') {
tokens.shift(); // throw away the '/'
result /= parseInt(tokens.shift());
}
else break;
}
return result;
}
function expr(tokens) {
let result = term(tokens); // was `parseInt(tokens.shift())`
while (true) {
if (tokens[0] === '+') {
tokens.shift(); // throw away the '+'
result += term(tokens); // was `parseInt(tokens.shift())`
}
else if (tokens[0] === '-') {
tokens.shift(); // throw away the '-'
result -= term(tokens); // was `parseInt(tokens.shift())`
}
else break;
}
return result;
}
function calc(tokens) {
let result = expr(tokens);
if (tokens.length) throw new Error('expected eof');
return result;
}
console.log(calc('2+2'.split('')) === 4); // true
console.log(calc('2+3-4'.split('')) === 1); // true
console.log(calc('2+2*2'.split('')) === 6); // true
console.log(calc('3+4*5'.split('')) === 23); // true
console.log(calc('3/2+4*5'.split('')) === 21.5); // trueКак видите, мы сразу заумели делать даже 3/2+4*5.
«(2+2)×2»
Что если всё-таки нужна восьмёрка при помощи скобок? Значит, нужно в term отвлечься на то, что заключено в скобки. А в скобках может быть то, что должно обрабатываться функцией expr , для чего мы её и выделили некоторое время назад. Очередное отвлечение назовём factor, из которой либо вызовем expr между скобками (круг замкнулся), либо считаем число.
function factor(tokens) {
if (tokens[0] === '(') {
tokens.shift();
let result = expr(tokens);
if (tokens[0] !== ')') {
throw new Error('missing closing parenthesis');
} else {
tokens.shift();
}
return result;
}
else return parseInt(tokens.shift());
}
function term(tokens) {
let result = factor(tokens);
while (true) {
if (tokens[0] === '*') {
tokens.shift(); // throw away the '*'
result *= factor(tokens);
}
else if (tokens[0] === '/') {
tokens.shift(); // throw away the '/'
result /= factor(tokens);
}
else break;
}
return result;
}
function expr(tokens) { /* omitted for clarity */ }
function calc(tokens) { /* omitted for clarity */ }
console.log(calc('2+2'.split('')) === 4); // true
console.log(calc('2+3-4'.split('')) === 1); // true
console.log(calc('2+2*2'.split('')) === 6); // true
console.log(calc('3+4*5'.split('')) === 23); // true
console.log(calc('3/2+4*5'.split('')) === 21.5); // true
console.log(calc('(2+2)*2'.split('')) === 8); // trueВ принципе, на этом заканчивается основа рекурсивного спуска. Дальше будем прокачивать эту структуру.
«(02. + 0002.) × 002.000»
До сих пор мы парсили массив символов, состоящий из цифр, бинарных операторов и круглых скобок. Каждый символ был токеном, и это очень упрощало нам жизнь. Но дальше развивать это будет сложно. Давайте теперь посимвольный split('') заменим чуть более взрослым лексическим разбором (по большому счёту это синоним токенизации).
У нас будет несколько регулярных выражений по всем типам токенов, и мы будем пытаться отрезать от входной строки по кусочку, который соответствует хоть одной регулярке. Сначала упрощённый пример, напрямую не связанный с нашей задачей:
const matchers = [
{ type: 'word', regex: /^[a-z]+/ },
{ type: 'number', regex: /^[0-9]+/ },
{ type: 'whitespace', regex: /^\s+/ },
];
let test = '123sdm k282rtk\tmx11';
while (test) {
for (const { type, regex } of matchers) {
const match = regex.exec(test)?.[0];
if (match) {
console.log({ type, match });
test = test.slice(match.length);
}
}
}
// {type: 'number', match: '123'}
// {type: 'word', match: 'sdm'}
// {type: 'whitespace', match: ' '}
// {type: 'word', match: 'k'}
// {type: 'number', match: '282'}
// {type: 'word', match: 'rtk'}
// {type: 'whitespace', match: ' '}
// {type: 'word', match: 'mx'}
// {type: 'number', match: '11'}Тут важно отметить ^ в начале каждого регулярного выражения, означающее поиск соответствия строго с начала строки. Вместе со slice() это даёт тот самый проход по строке «кусочками».
Такой лексер на регулярках очень компактен и читабелен, но его гибкость и производительность весьма ограничены для по-настоящему взрослого лексического разбора; имейте это в виду, когда пойдёте делать свой язык программирования. Тем не менее, современные рантаймы JS оптимизируют разрезание строк через slice, по сути сводя его к манипуляциям с указателями. В сумме с простыми регулярками, прибитыми к началу строки, это должно давать неплохую производительность.
Давайте теперь растянем такой лексер на лексику наших выражений. Вместо строк для обозначения типов возьмём JS-овский Symbol и упакуем матчинг внутрь функции-генератора (это такие функции, которые могут выдавать по несколько значений за один вызов; в JavaScript они обозначаются звёздочкой и «выплёвывают» значения через yield).
const
WS = Symbol('ws'),
NUMBER = Symbol('num'),
PLUS = Symbol('plus'),
MINUS = Symbol('minus'),
MULTIPLY = Symbol('mul'),
DIVIDE = Symbol('div'),
LEFT_PAR = Symbol('lpar'),
RIGHT_PAR = Symbol('rpar'),
END_OF_FILE = Symbol('eof');
function* tokenize(input) {
const matchers = [
{ type: NUMBER, re: /^[0-9\.]+/ },
{ type: PLUS, re: /^\+/ },
{ type: MINUS, re: /^[-−]/ },
{ type: MULTIPLY, re: /^[*×⋅]/ },
{ type: DIVIDE, re: /^\// },
{ type: MOD, re: /^%/ },
{ type: WS, re: /^[\s]+/ },
{ type: LEFT_PAR, re: /^\(/ },
{ type: RIGHT_PAR, re: /^\)/ },
{ type: END_OF_FILE, re: /^$/ }
];
let pos = 0;
while (input) {
for (const { type, re } of matchers) {
const match = re.exec(input.slice(pos))?.[0];
if (typeof(match) === 'string') {
yield { type, pos, match };
if (type === END_OF_FILE) input = null; // breaks outer loop
pos += match.length;
break;
}
}
}
}
for (const token of tokenize('(2+2)×2')) {
console.log(token);
}
// {type: Symbol(lpar), pos: 0, match: '('}
// {type: Symbol(num), pos: 1, match: '2'}
// {type: Symbol(plus), pos: 2, match: '+'}
// {type: Symbol(num), pos: 3, match: '2'}
// {type: Symbol(rpar), pos: 4, match: ')'}
// {type: Symbol(mul), pos: 5, match: '*'}
// {type: Symbol(num), pos: 6, match: '2'}
// {type: Symbol(eof), pos: 7, match: ''}
for (const token of tokenize(' 234 ')) {
console.log(token);
}
// {type: Symbol(num), pos: 1, match: '234'}
// {type: Symbol(ws), pos: 4, match: ' '}
// {type: Symbol(eof), pos: 5, match: ''}Не знаю, заметили вы сами или нет, но здесь мы впервые разобрали выражение (2+2)×2 - обратите внимание на знак умножения, это не звёздочка, причём воспринимается наравне со звёздочкой. Там есть ещё один вариант умножения, а также «типографский» минус. Пускай это будет фишкой нашего языка для упоротых по типографике эстетов.
В сущности, это то же самое, что split(''), только кусочки покрупнее. Среди прочего у нас теперь есть явное обозначение пробелов (whitespace), которые мы легко можем пропустить, и end-of-file в виде отдельного токена.
Но дело не ограничивалось одним лишь split(''), правда? Мы подглядывали следующий токен через if (tokens[0] === '*'), а также «проглатывали» токены через shift(). Кое-где мы даже убеждались, что токен именно такой, а не другой, выбрасывая ошибку 'missing closing parenthesis'. Воспроизведём эти удобства в классе:
class ExpressionCalc {
#stream;
#token;
constructor(input) {
this.#stream = tokenize(input);
this.#next();
}
#error(err) {
throw new Error(`${err}, pos=${this.#token?.pos}, token=${this.#token.match}, type=${this.#token.type.description}`);
}
#next() {
do {
this.#token = this.#stream.next()?.value;
} while (this.#token?.type === WS);
}
#accept(type) {
let match;
if (this.#token?.type === type) {
match = this.#token.match;
this.#next();
return match || true;
}
return false;
}
#expect(type) {
return this.#accept(type) || this.error(`expected ${type.description}`);
}
}Это джентельменский набор для простейшего парсинга:
метод
next()— эквивалентshift()из массива с автоматическим пропуском пробелов;метод
accept(type)— эквивалент проверки с последующим удалением из массива; заодно возвращает текст совпадения;метод
expect(type)— эквивалент проверки с выбрасыванием ошибки при несовпадении;метод
error(err)— выбрасывание ошибки с индикацией текущей позиции.
То есть всё это у нас было, но прямо по месту парсинга, "inline". Давайте теперь адаптируем функции парсинга/вычисления как методы того класса:
class ExpressionCalc {
...constructor, #error, #next, #accept, #expect
#factor() {
let result;
let text;
if (this.#accept(LEFT_PAR)) { // parenthesis (but not function calls)
result = this.#expression();
this.#expect(RIGHT_PAR);
} else if (text = this.#accept(NUMBER)) { // numeric literals
result = parseFloat(text);
} else {
this.#error('unexpected input');
}
return result
}
#term() {
let result = this.#factor();
while (true) {
if (this.#accept(MULTIPLY)) result *= this.#term();
else if (this.#accept(DIVIDE)) result /= this.#term();
else if (this.#accept(MOD)) result %= this.#term();
else break;
}
return result;
}
#expression() {
let result = this.#term();
while (true) {
if (this.#accept(PLUS)) result += this.#term();
else if (this.#accept(MINUS)) result -= this.#term();
else break;
}
return result;
}
}Пробуем:
console.log(new ExpressionCalc('2+2').calc() === 4); // true
console.log(new ExpressionCalc('2+3-4').calc() === 1); // true
console.log(new ExpressionCalc('2+2*2').calc() === 6); // true
console.log(new ExpressionCalc('3+4*5').calc() === 23); // true
console.log(new ExpressionCalc('3/2+4*5').calc() === 21.5); // true
console.log(new ExpressionCalc('(2+2)*2').calc() === 8); // true
console.log(new ExpressionCalc('(02. + 0002.) × 002.000').calc() === 8); // true
console.log(new ExpressionCalc('3%2').calc() === 1); // trueЕщё у нас появилась операция получения остатка от деления (оператор %) и числа дробные поддерживаются, т.к. вместо parseInt делаем parseFloat.
«+1»
Как бы нам добавить сюда унарный плюс и унарный минус? По первой интуиции это знак рядом с числовым литералом, который можно учесть подобно скобкам в factor. Но это обманчивая интуиция. Возможны такие выражения: -(2+3), -sin(0.33). Стало быть, это отдельная вещь c отдельной рекурсией.
#factor() {
let result;
...
} else if (this.#accept(PLUS)) { // unary plus
result = +this.#factor();
} else if (this.#accept(MINUS)) { // unary minus
result = -this.#factor();
}
...
return result
}
console.log(new ExpressionCalc('+1').calc() === 1); // true
console.log(new ExpressionCalc('-(2+3)').calc() === -5); // true«cos(2*pi)»
Именованные операнды типа "pi" чем-то напоминают числовые литералы, не правда ли? По крайней мере они стоят там же относительно операторов. Ну, например, 2 + -(5 * 3) vs 2 + -(pi * 3). Похоже? И несложно представить себе какие-нибудь римские числа, которые вообще не отличаются от переменных: 10 + 21 = 10 + XXI. Только с функциями какая-то фигня: у них свои скобки. Значит, и будем обрабатывать всё там же, где числа — в factor.
#factor() {
let result;
let text;
...
} else if (text = this.#accept(IDENTIFIER)) { // identifiers (named constants and function calls)
text = text.toLowerCase();
let func;
if (text === 'pi') result = Math.PI;
else if (text === 'e') result = Math.E;
else if (Math[text] && typeof (func = Math[text]) === 'function') {
this.#expect(LEFT_PAR);
result = func(this.#expression());
this.#expect(RIGHT_PAR);
}
else this.#error(`unknown id ${text}`);
}
...
return result
}
console.log(new ExpressionCalc('cos(2*pi)').calc() === 1); // trueНа что тут можно обратить внимание? Во-первых, мы не пытаемся как-либо реюзать обработку приоритезирующих скобок; здесь скобки — это отдельная синтаксическая конструкция. Если бы мы поддерживали несколько аргументов, то прошлись бы здесь по ним через запятую. Во-вторых, что мы реюзаем, так это функции Math из JavaScript.
Можно сказать, что переменные, которые вы определяете в этом блоке, образуют окружение, в котором вычисляется введённая вами формула (ну или «исполняется ваш скрипт» если бы мы писали интерпретатор какого‑нибудь языка).
«-2.1+ .355 / (cos(pi % 3) + sin(0.311))»
console.log(new ExpressionCalc('-2.1+ .355 / (cos(pi % 3) + sin(0.311))').calc());
-1.8260809473359578
// Проверка в браузере:
// -2.1+ .355 / (Math.cos(Math.PI % 3) + Math.sin(0.311))
// -1.8260809473359578Как обещано.
Бонус-трек: мусор в лексере
В текущем виде лексер вообще не способен его обрабатывать. Чтобы избежать падения на каком-нибудь там }@5+1, можно пропускать по одному символу, пока совпадения вновь не появятся, и что с ними дальше делать, уже зависит от применения; в общем случае надо показать ошибку и прекратить вычисление. Хорошим тоном будет накопить неизвестные символы и выдать их одной ошибкой.
const
...
UNKNOWN = Symbol('unknown'),
...;
function* tokenize(input) {
const matchers = [
...
];
let pos = 0;
let unknownFrom = -1;
while (input) {
const posBefore = pos;
for (const { type, re } of matchers) {
const match = re.exec(input.slice(pos))?.[0];
if (typeof(match) === 'string') {
if (unknownFrom >= 0) {
// flush the unknown input as one token
yield {
type: UNKNOWN,
pos: unknownFrom,
match: input.slice(unknownFrom, pos),
};
unknownFrom = -1;
}
yield { type, pos, match };
if (type === END_OF_FILE) input = null; // breaks outer loop
pos += match.length;
break;
}
}
if (input && posBefore === pos) {
// nothing matched, track unknown input
if (unknownFrom < 0) unknownFrom = pos;
pos++;
}
}
}
[...tokenize('}@5+1')].forEach(t => console.log(t));
// {type: Symbol(unknown), pos: 0, match: '}@'}
// {type: Symbol(num), pos: 2, match: '5'}
// {type: Symbol(plus), pos: 3, match: '+'}
// {type: Symbol(num), pos: 4, match: '1'}
// {type: Symbol(eof), pos: 5, match: ''}Подытоживая
Целью заметки было показать «на пальцах», как работает и из чего строится простейший рекурсивный парсер-калькулятор арифметических выражений, не погружаясь в термины грамматик языков программирования. Подобные парсеры можно встретить под капотом софта, который на уровне пользователя позволяет вводить формулы/выражения, например для срабатывания алертов или для формирования графиков. Встречаются и другие подходы к обработке выражений: перевод в постфиксную форму с последующим вычислением, применение генераторов парсеров вместо ручного их написания. Многие языки и среды исполнения предлагают готовые решения, чтобы вычислять пользовательские выражения.
Код
XXL: jdoodle.com/ia/Kmt


loginsin
Как насчёт выражений: a=1; b=2; x=pi/3; abcos(x) ?
YegorP Автор
В устоявшихся терминах парсинга это три инструкции (statement), а не просто одно выражение (expression). Это уже практически императивный язык. Тут появляется много нового: окружение с переменными, право-ассоциативный оператор (=), бэктрекинг/доразбор для обработки abcos как a*b*cos. Тянет на отдельный пост.
Alexandroppolus
Сомнительная идея, имхо. Начнутся всякие неоднозначности, например bacos - это b * a * cos или b * acos (арккосинус).
YegorP Автор
Да. Но справедливости ради, такие же неоднозначности возможны и в рукописной форме на бумаге. Это уже вопрос дизайна языка. Если вы дизайните ЯП общего назначения, то решение так себе. Но для чего-то специализированного может быть приемлемо. Даже интересно эти неоднозначности определить и выдать предупреждения/ошибки.
loginsin
Да можно добавить оператор ";", который ничего не делает: всё остальное (вычислит выражения слева и справа) сделает "вычислитель". Но переменные - да, вводить придётся.