Композиция математических объектов в рамках абстрактной модели мышления / forpes.ru

Главная
Композиция математических объектов в рамках абстрактной модели мышления

Композиция математических объектов в рамках абстрактной модели мышления +8

30.07.2023 20:30

Ramayasket 150 2300 Источник

УДК 510.2, 004.8

Посвящается моим родителям

Помощь в работе оказал к.ф.-м.н. Ленюк С. В., доцент каф. выс. мат. МФТИ.

Аннотация

Рассматривается структура основных математических объектов, опирающаяся на абстрактную модель разумного мышления. Каковая, в свою очередь, выводится из основополагающего высказывания "я мыслю, следовательно, существую". Показано, что данные аспекты математики взаимосвязаны и могут быть заданы только в рамках объединяющей теории.

Ключевые слова: абстрактная модель мышления, смешанные системы, математическая реальность, низшая математика, ФОРАОН, формальная семантика, темпоральная механика.

Библиография: 3 наименования.

1. Введение

Потребность в настоящей работе обусловлена комплексом проблем (открытых вопросов) современной науки. Эти проблемы относятся, с одной стороны, к теории искусственного интеллекта, а с другой -- к основаниям математики. Опишем их вкратце.

В отношении ИИ, можно указать, что эта область знаний не имеет общепризнанного, твёрдого и законченного теоретического фундамента, имея в виду строгую математическую модель мышления: компоненты и структура мыслящей системы, её цели и алгоритмы их достижения. Человечество возлагает на ИИ большие надежды и направляет на его развитие значительные усилия. Поэтому, обнаружение математической модели мышления видится крайне актуальной задачей.

В области оснований математики, укажем проблему композиции. Математические конструкции могут быть весьма сложны, но всё сложное состоит из более простого, а в современной математике поиск наиболее простого обнаруживает сразу несколько объектов, среди которых, например, логические значения, мнимая единица, пустое множество, и т.д.. Разбиение подобных объектов на более простые не описано.

Но, незнание композиции не эквивалентно её отсутствию. Указанные объекты различаются в поведении, что говорит в пользу различий и в структуре. Исследовать данную область представляется совершенно необходимым: знание структуры объекта эквивалентно доказательству описывающих этот объект аксиом. Кроме того, решение этой проблемы позволит научить ИИ понимать математику.

Работа в этом направлении была начата в 2013 году. В ходе исследования было обнаружено, что две упомянутые проблемы могут быть решены только совместно. Как показало исследование, между математикой и мышлением есть фундаментальная связь, ввиду которой предъявить композицию указанных математических объектов можно только в рамках модели мышления.

Изложение результатов проведённого исследования превышает по объёму журнальную статью, поэтому материал разделён на несколько частей, каждая из которых оформляется в виде отдельной статьи. Данная первая статья описывает решение проблемы композиции математических объектов.

2. Парадигма

2.1. Принципы

Данная статья описывает и обсуждает абстрактную модель мышления (АММ). Слова "мышление" и "разум" полагаем синонимами.

Источником необходимости для АММ являются наши знания о мышлении: если модель верна, то мы можем безусловно ожидать от неё тех или иных черт. Мы будем неоднократно возвращаться к мышлению как к источнику необходимости; сейчас укажем на два аспекта, важных для всей статьи.

Первый аспект связан с тем, что мышление способно думать абсолютно обо всём, вне зависимости от существования предмета рассуждений. Данный тезис будем называть принципом универсальности.

Пример: вещественное число, отличное от нуля, либо положительно, либо отрицательно. Тогда пусть число, которое одновременно больше и меньше нуля, называется "чудесным". Существуют такие числа или нет, принцип универсальности требует, чтобы сама возможность их формализации не выходила за рамки АММ, в противном случае эта модель не будет исчерпывающей.

Этот пример иллюстрирует действие принципа универсальности при обосновании необходимости. Если тем или иным образом обоснована необходимость некоторого правила, то принцип универсальности, в свою очередь, обосновывает необходимость нарушения этого правила.

Второй аспект связан с внутренним представлением знаний и независимостью мышления от языка. Очевидно, что базовое мышление ребёнка успешно функционирует даже до того, как он начинает понимать и применять свой первый язык, в противном случае он не мог бы этого сделать.

Чтобы подобное стало возможным для АММ, она должна обладать встроенным способом хранения знаний, который представляет структуру объектов напрямую, т.е. выражает их композицию, а не кодирует их при помощи третьих объектов. Данный тезис будем называть принципом независимости.

2.2. Смешанные системы

В самых разных системах, хранение и изменение каких-либо объектов суть две наиболее низкоуровневые, первичные, основополагающие функции. Для выполнения этих функций в системе должна присутствовать память, хранящая объекты, и время, их изменяющее. Тройку $\{m,t,x\}$ будем называть смешанной системой (англ. mixed system), где память обозначена как , время как , а объекты в памяти как .

Природа создаёт смешанные системы самой разной сложности. Так, одну из самых простых образуют кварки и глюоны. Действительно, кварки хранят цвет, а глюоны его меняют; таким образом, кварки играют роль памяти, глюоны роль времени, а цвет есть хранящийся в памяти объект.

На другом конце шкалы сложности находится мозг человека и знания. Нейроны выполняют роль памяти, а нервные импульсы роль времени. Отсюда происхождение термина "смешанная" система, которая состоит как из материальных (нейроны, импульсы), так и из абстрактных (знания) элементов.

Среди теоретических или искусственных систем, самые очевидными примерами являются машина Тьюринга и компьютер. В машине Тьюринга роли памяти, времени и объектов играют лента, головка и символы, соответственно. В ЭВМ данные в оперативной памяти изменяются процессором.

Альтернативный термин для смешанной системы -- вариальность (англ. variality).

2.3. Математическая реальность

Поскольку разум человека является смешанной системой, АММ должна включать в себя представление памяти и времени. Задавшись вопросом о природе подобного представления, мы вынуждены для начала исключить такие абстракции, как нейронная сеть и машина Тьюринга.

Что касается нейронной сети, то данная структура моделирует не разум, а мозг, что не соответствует задачам настоящего исследования: переход от взаимодействия нейронов и импульсов к мышлению есть переход от количества к качеству, который не учитывается нейронной сетью как моделью.

Машину Тьюринга также следует исключить, т.к. лента не даёт возможность представлять структуру объектов напрямую; символы всего лишь кодируют её при помощи некоторого языка. Содержимое ленты нуждается в интерпретации в рамках этого языка, что не соответствует принципу независимости.

Таким образом, необходимо предъявить другую модель памяти/времени, соответствующую принципам универсальности и независимости. Весьма удачно, что такая модель обнаруживается достаточно легко: она прослеживается в истории человеческого интеллекта от доисторических времён до наших дней.

Одним из ранних свидетельств разума является наскальная живопись. Для неё нужна была поверхность (стена пещеры, возможно) и средство нанесения рисунка. Однажды появившись, средства письма остались с людьми навсегда, изменяясь технически, но не по сути.

Будем сокращённо называть поверхность для письма доской, а средство нанесения рисунка маркером. Смешанную систему, в которой доска является памятью, а маркер временем, будем называть математической реальностью. В данной модели, надписи на доске играют роль объектов смешанной системы.

В центре данной работы лежит идея использовать математическую реальность как представление памяти и времени в АММ и математике в целом. Плюсом этого подхода является то, что математика полагает средства письма самоочевидными.

2.4. Начальный постулат

Отправной точкой наших рассуждений является известное из философии высказывание "я мыслю, следовательно, существую" (начальный постулат, НП). Уточним, что НП не является аксиомой: его нет нужды принимать на веру, т.к. способность формулировать осмысленные высказывания уже доказывает и разумность, и существование их автора.

Это утверждение Декарт выдвинул как первичную достоверность, истину, в которой невозможно усомниться -- и с которой, следовательно, можно начинать отстраивать здание достоверного знания (Википедия).

Математическую теорию, вытекающую из начального постулата, будем называть низшей математикой (англ. lower mathematics). Имея в виду столь надёжный фундамент (НП), мы можем ожидать, что подобная теория будет в состоянии решить задачи, упомянутые во введении. Во-первых, формально описать композицию основных математических объектов. И во-вторых, математически описать цели мышления и способы их достижения. Эти две части теории будем называть, соответственно, общей и специальной.

Данная статья описывает первую часть теории. Совокупность её определений будем называть формальный аппарат общего назначения (ФОРАОН, англ. formal apparatus of overall notion, FORAON). Определения даются при помощи оригинальной графической нотации и программного кода на языке C#, дополняющих друг друга. Для каждого вводимого объекта, мы указываем цепочку обоснования, т.е. путь вывода его необходимости из НП, а также понятийный и информационный состав объекта.

2.5. Формальная семантика

Традиционно, математика связывает понятие формальности с языками, ассоциируя с ними термины "символ", "алфавит", "слово". При этом, слова кодируют смысл (семантику) объекта, а способ сопоставления слов и смысла и образует, собственно, формальный язык.

Однако, такой способ построения языка не обеспечивает передачу структуры.

Формальной семантикой будем называть способ представления смысла, явно (напрямую) выражающий структуру. Данная работа обнаруживает, что математическая реальность достаточно богата для этого.

2.6. Программная нотация

Программные определения, приведённые в статье, доступны на сайте по адресу https://mixed.systems/FORAON. Объектам ФОРАОН даны названия в нотации underscore_case, а библиотечные классы и методы именуются в нотации PascalCase.

Мы используем язык программирования, чтобы выразить структуру излагаемой идеи, поскольку язык программирования на 100% однозначен, а также лаконичнее естественного языка. Код явно указывает композицию объекта, и других "неучтённых" элементов не подразумевается.

Код ФОРАОН не является утилитарным ПО или прикладным интерфейсом (API). Также, он не делает попытку покрыть полностью материал статьи (такая попытка эквивалентна написанию нового языка программирования). Классы ФОРАОН следует рассматривать как фрагменты кода или приёмы, используя которые, можно построить программу для конкретного случая. Эти классы объединены в проект, который можно компилировать и выполнять.

3. Структура АММ

3.1. Предел осознания

Начнём разбирать НП. Мы будем анализировать как смысл, так и запись этой фразы.

Укажем, что НП высказан от первого лица, т.е. он имеет смысл для некоторого разумного субъекта. Чтобы отразить данный факт, в структуре АММ должна быть часть, соответствующая слову "я". Мы будем называть эту часть АММ термином внимание.

Формальное определение внимания: public class attention { }. Для целей статьи достаточно задать его как класс без содержания -- важно само наличие внимания в составе АММ; в специальной части теории это определение будет расширено. В формулах будем обозначать внимание символом $\underline{\varphi}$ .

Слово "мыслю" обосновывает необходимость памяти и времени в составе АММ. Одновременно, из записи НП следует, что доска и маркер являются моделями этих понятий. Поскольку использование средств письма не вызывает у математиков затруднений, мы можем включить доску и маркер в АММ и применять их для обоснования необходимости.

Смешанная система (вариальность), входящая в состав мышления, моделируется классом variality. Как видно из определения, членами этого класса являются доска и маркер (board и marker), подробнее описанные далее.

public partial class variality {

    public static board memory;
    public static marker time() => new(); }

В свою очередь, attention и variality комбинируются в классе sentience, отражающем структуру мышления в целом. Данный класс является корневым определением АММ. Таким образом, в состав АММ включены понятия, необходимость которых вытекает из "я мыслю".

public partial class sentience {

    public static attention personality;
    public static variality mixed; }

Обратимся к слову "существую". Для человека, оно означает материальный характер мышления, присутствие разума в физическом мире. В математике, "существую" будем трактовать как указание на то, что входящие в АММ объекты образуют отдельную (в противоположность знаниям) категорию, аналогичную материальным элементам разума. Эти объекты будем называть собственными (англ. own objects).

Исследуя сам себя, разум способен осознать собственные объекты: внимание, память и время, но и только. Обнаружить более детальную структуру (нейроны и импульсы) при таком исследовании нельзя. Мы будем называть границу самоочевидных знаний о мышлении пределом осознания.

3.2. Доска

Математика полагает использование поверхности для письма естественным, что даёт возможность использовать свойства доски при обосновании необходимости.

Для нас представляют интерес следующие аспекты поверхности (её размер не рассматривается):

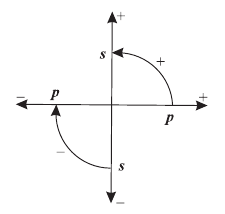
два измерения (оси) -- первичной и вторичной ориентации;
на каждой оси два направления -- положительное и отрицательное;
преобразование осей и направлений при помощи поворотов, имеющих направление.

В настоящей работе выбраны ориентации и направления, как показано на Рис. 1. Первичная и вторичная оси обозначены как p и s, положительные и отрицательные направления как и . По умолчанию принимаются: положительное направление и первичная ориентация.

Соответствующее программное определение:

public class board {

    public enum drn { p = 0, n = 1, }
    public enum orn { p = 0, s = 1, }
    public delegate void rotate(object x, drn d); }

В классе board направления и ориентации представлены соответственно как drn и orn, а поворот как делегат rotate. Направления и ориентации моделируются как перечисления (enum) со значениями . Это значит, что мы не видим в них каких-либо свойств, кроме отличия одного значения от другого.

В формулах будем обозначать доску символом $\mathscr{B}$ .

3.3. Маркер

Время с необходимостью входит в понятие мышления. Оно делает возможными действия, в частности, изменения. Мы будем рассматривать время в отрыве от его физического аспекта, что делает возможным рассмотреть выполнение любой конечной или бесконечной цепочки действий.

Запись НП обосновывает использование маркера как модели времени.

Чтобы описать использование маркера, надо абстрагироваться от человека, стоящего с маркером у доски. В нашем рассмотрении есть только внимание, доска и маркер. Следовательно, в рамках АММ всё взаимодействие с доской должно выполняться маркером. Описание маркера начнём с базового сценария, в котором внимание инициирует запись какого-либо объекта на доске. Поведение маркера выглядит так:

получить от внимания объект, подлежащий записи;
записать этот объект на доске.

Мы исходим из того, что получение данных и последующая запись на доске отстоят во времени. Хотя мы не рассматриваем физический аспект времени, однако на концептуальном уровне будем выделять предыдущий и последующий моменты. В силу этого, маркер должен иметь встроенную память для хранения полученного объекта.

Всё вышесказанное записывается на C#:

public class marker {

    public object argument;
    public void function(object previous, object next) {

        argument = read(previous);
        write(next, argument); }}

Рассмотрим код подробнее. Класс marker содержит два члена: поле argument, представляющее собой память маркера, и метод function, описывающий поведение маркера.

Маркер взаимодействует с двумя объектами, которые будем называть коммутаторами: предыдущий (previous) и следующий (next). В базовом сценарии предыдущим коммутатором является внимание, следующим -- доска (вместе с тем, принцип универсальности требует, чтобы маркер не ограничивал диапазон возможных в качестве коммутаторов объектов).

Метод function состоит из двух частей. Первая (строка 6) читает информацию из предыдущего коммутатора и копирует её в память маркера. Вторая -- записывает её в следующий коммутатор (строка 7).

Важный аспект маркера, вытекающий из базового сценария: как и всякое средство записи, маркер должен предоставить гарантию, что предыдущий коммутатор не будет изменён: действительно, процесс записи на доске не должен изменять содержание внимания (чтение не должно изменять объект).

Для этого, необходимо обработать случай, когда один и тот же объект передан маркеру в качестве как предыдущего, так и следующего коммутатора. В этом случае запись нужно отменить (подчеркнём, что от записи защищено не внимание, а именно предыдущий коммутатор) -- строка 4. На языке C# это выражается через аппарат исключения.

    public void function(object previous, object next) {

        argument = read(previous);
        if (previous == next) throw new Exception();
        write(next, argument); }

На этом базовый сценарий завершён.

Чтобы произвести чтение, достаточно лишь выполнить маркер, передав доску в качестве предыдущего, а внимание в качестве следующего коммутатора. Таким образом, как запись на доске, так и чтение с неё могут в равной степени выполняться маркером как средством передачи информации.

Базовый сценарий полагает, что маркер записывает информацию (argument) без изменений. Однако, принцип универсальности требует, чтобы нарушение этого правила, т.е. изменение информации между чтением и записью, также поддерживалось. Понятие изменения или преобразования напрямую вытекает из начального постулата: "мыслю" подразумевает, что содержимое памяти может меняться.

Для поддержки изменения добавим в класс marker два члена:

    public dynamic transform;
    public drn direction;

Чтобы маркер мог изменять информацию, нужен объект, описывающий требуемое изменение. Таким объектом является поле transform, добавленное к коду маркера. Второе добавленное поле (direction) указывает на направление изменения. Мы исходим из того, что преобразование может иметь прямое или обратное направление (в некоторых случаях обратное преобразование отменяет прямое, и наоборот). Положительное направление соответствует прямому, отрицательное -- обратному преобразованию.

Перепишем функцию function:

public void function(object previous, object next) {

    argument = read(previous);
    argument = transform(argument, direction);

    if (previous == next) throw new Exception();
    write(next, argument); }

Строка 4 выполняет transform в указанном направлении, и записывает результат в память маркера.

Таким образом, мы взяли за основу самоочевидные аспекты маркера в виде базового сценария и рассмотрели расширение и нарушение этого сценария. Результатом этого стала модель, представляющая математические аспекты маркера, вытекающие из начального постулата. Отметим, что данная модель в точности соответствует процессу вычисления функции, хотя математика и не акцентирует внимание на защите аргумента от записи.

В формулах будем обозначать маркер символом $\mathscr{M}$ .

Определение маркера в графической нотации даётся в 4.10.

3.4. Ластик

Менее очевидным, но всё же необходимым определением является ластик $\mathscr{E}$ . Его необходимость следует из того, что сама по себе запись является обращаемой операцией. Т.к. любые операции в АММ выполняются маркером, ластик является просто признаком того, что объект нужно стереть.

Ластик задаётся как пустой класс public class eraser { }, т.к. мы не усматриваем в нём каких-либо свойств. Чтобы выразить на C# способность ластика стирать объект, заменим последнюю строчку в коде маркера следующим кодом:

    if (argument is eraser) erase(next);
    else write(next, argument);

Например, применение ластика к доске как таковой очищает всю память.

4. Абстрактные объекты

4.1. Универсальные термины

Необходимость понятия "объект" как предмета рассуждений следует из "мыслю", и других определений не требуется. По принципу универсальности, объектом может являться всё что угодно.

Ключевым свойством объектов является их способность состоять из частей.

Так, начальный постулат является цельной фразой с законченным смыслом. В то же время, он состоит из элементов (слов). Другими словами, НП является системой; таким образом, необходимость термина "система" также напрямую вытекает из этой фразы.

Суть понятия системы программно выражается классом system:

public abstract partial class system {
    public abstract system[] parts(); }

Данный класс определяет функцию parts(), которая возвращает набор элементов системы. Отметим, что эта функция является иллюстративной: структура объектов, как правило, более сложная, чем это может быть однозначно выражено последовательностью. Система не обязана иметь элементы (см. 4.2), но если они есть, их должно быть более одного: единственный объект не образует новую систему.

В соответствии с принципом универсальности, можно также рассмотреть (несуществующий) объект, который входит в состав своих же частей: например, записать parts() => new[] { this, ... }. Рекурсивные по parts() алгоритмы, обрабатывающие такое определение, будут зацикливаться; однако, это указывает не на некорректность самого понятия системы, а лишь на то, что несуществующие объекты отличаются в поведении от существующих (более подробно о существовании см. 5.4, 7.3).

Термины "объект" и "система" будем называть универсальными.

4.2. Нуль-система

Систему без элементов (пустую) будем называть нуль-системой (класс empty):

public class empty : system {
    public override system[] parts() => new system[]{}; }

Графическая нотация ФОРАОН изображает нуль-систему как кружочек (Рис. 2). Его размер не фиксируется и может меняться для удобства. Этот кружочек называется примитивом.

В формулах будем обозначать нуль-систему символом $\underline{\alpha}$ . Из определения следует, что $\underline{\alpha}$ является простейшим объектом и конечным этапом рекурсивной декомпозиции входной системы.

Мы будем выделять особенный примитив из числа входящих в состав сложного объекта, с которого начинается процесс его конструирования (он же отвечает за представление объекта в целом). Данный примитив будем называть базисом объекта. В программной нотации, базису объекта соответствует поле public empty basis, добавленное в класс system.

4.3. Дискриминаторы

Принципиальная функция памяти заключается в хранении объектов. А именно, память АММ должна хранить множественные объекты, из чего следует, что необходим способ отличать экземпляры объектов в памяти друг от друга. Такой способ будем называть дискриминатором.

Различные виды памяти реализуют различные способы различения объектов. Например, для памяти машины Тьюринга дискриминатором является позиция (номер ячейки) на ленте. Это позволяет в разные ячейки поместить символы и ссылаться на них и изменять их по отдельности. Аналогично, в оперативной памяти ЭВМ дискриминатором является адрес объекта.

Рассмотрим дискриминаторы на доске. Первым и самым очевидным из них является место (координаты) объекта на доске. По сути, это аналог номера ячейки, с поправкой на двухмерность доски.

Характерно, что для одного (изолированного) объекта его размещение не существенно: будь то доска, лента или память ЭВМ, не важно, где он расположен. Координаты объекта играют роль тогда, когда рассматриваются несколько объектов, взаимно расположенные в памяти тем или иным образом.

Кроме координат, доска имеет также два дополнительных дискриминатора: направления и ориентации. Отметим, что это более сложные, независимые способы отличать объекты друг от друга: действительно, одна точка не может задать ни направление, ни ориентацию.

Использование этих дискриминаторов более подробно рассмотрено ниже. Характерно, что ни лента машины Тьюринга, ни RAM не содержат дополнительных дискриминаторов, а именно ими объясняется то "богатство" математической реальности, о котором говорилось в 2.5.

Для учёта дискриминаторов, добавим новый член place (размещение) к классу system:

public abstract partial class system {
    public object place; }

Рассмотрим следующий код. В классе discriminator два (в остальном одинаковых) члена различаются по именам, т.е. система имён в языке программирования представляет собой разновидность дискриминатора. Указанный абстрактный класс является основой для других определений ФОРАОН, при этом совместно с ним используются различные дискриминаторы на доске.

public abstract class discriminator : system {
    public system o1;
    public system o2; }

Значения (place и аналогичные), связанные с дискриминаторами, будем называть информацией.

Завершая описание дискриминаторов, нужно отметить, что они относятся к конкретному устройству памяти. Так, мы ничего не знаем о том, какие дискриминаторы есть в нейронной сети мозга. Можно, однако, предположить, что память человека не менее богата, чем доска.

4.4. Контракт

Первым из объектов, более сложных, чем $\underline{\alpha}$ , является контракт. Для его построения будем использовать один из дискриминаторов, а именно направления на доске. Построение контракта начнём с одиночного примитива (базис), вслед за которым запишем по одному примитиву в положительном и отрицательном направлении от базиса. Эти два примитива будем называть полюсами контракта.

Определение контракта в графической нотации изображено на Рис. 3. Ось, вдоль которой расположены полюсы, обозначена символом "коннектор" (короткая линия). В статье, расстояние между полюсами может меняться для удобства восприятия, но с математической точки зрения мы считаем, что это расстояние является некоторой элементарной величиной.

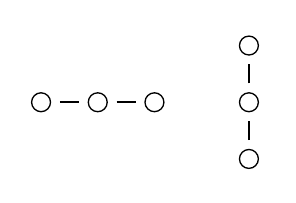
Мы можем рассматривать или не рассматривать ориентацию оси, по которой размещён контракт. Если ориентация не рассматривается, то изображения по вертикали и горизонтали эквивалентны; также допускается изображение под углом или изогнутое. Если же ориентация рассматривается, то поле place контракта принимает одно из значений orn, изображения по горизонтали и вертикали получают разный смысл, а коннектор изображается двойной линией (Рис 4).

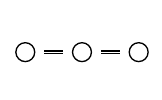
Рассмотрим программное определение контракта. Здесь o1 и o2 представляют полюсы, а конструктор contract() отражает последовательность построения объекта. Функция parts() возвращает его элементы: базис, положительный и отрицательный полюсы.

public class contract : discriminator {

    public contract() {
        basis = new empty();
        (o1, o2) = (new empty(), new empty());
        (o1.place, o2.place) = (drn.p, drn.n); }

    public override system[] parts() => new[] { basis, o1, o2 }; }

В формулах будем обозначать контракт символом $\underline{\omega}$ .

4.5. Краски

Мы будем применять дополнительные элементы графической нотации для иллюстрации расположения примитивов в контракте и соответствующих значений place. Эти элементы для "раскрашивания" примитивов будем называть краски. Поскольку применение разных цветов в статье непрактично, будем использовать черно-белые элементы, см. Рис. 5.

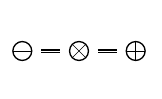
Ещё один вид краски рассмотрен далее в статье (см. 4.10).

4.6. Порядок

Одним из понятий, вытекающих из начального постулата, является отношение порядка (следования), т.е. "предыдущий" и "следующий". Необходимость порядка следует как из упорядоченности слов в записи НП, так и из предыдущего и следующего моментов времени.

Отношение порядка традиционно изображается в виде стрелочки (запись в нотации ФОРАОН см. 4.8). Запись объекта перед стрелочкой означает, что объект рассматривается, конструируется, обрабатывается или выполняется перед объектом, стоящим после стрелочки (связь порядка с временем).

Отношение порядка между двумя объектами (т.е. указание на один из них) требует одного бита информации. В программной нотации, отношение порядка будем моделировать классом order, в котором для указания на один из объектов o1, o2 используется направление (drn).

public abstract class order : discriminator {

    public drn direction;
    public system selected() => new[] { o1, o2 }[(int)direction]; }

Стрелочка имеет два смысловых наполнения. Для пары объектов, она задаёт их порядок. Кроме того, если объектов более двух, то стрелочка указывает, какие из этих объектов образуют пару.

4.7. Акцент

Традиционно, символ записывается на доске, и других вариантов не предусмотрено. В ФОРАОН, в силу принципа универсальности, примитив можно надписать как прямо на доске, так и поверх другого примитива, так что функцию памяти играет объект, отличный от доски. Данный вариант расположения примитивов имеет название акцент (accent).

Графическое определение акцента дано на Рис. 6.

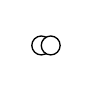
Программное определение:

public class accent : discriminator {
    public override system[] parts() => new system[]{}; }

В данном классе нижний примитив соответствует полю o1, верхний полю o2; при этом поля o1 и o2 упорядочены в памяти программы, нижний и верхний примитивы также упорядочены между собой графически. Отметим, что данные поля не входят в функцию parts() акцента. Причина этого в том, что сам факт надписывания одного примитива над другим не состоит из элементов.

В формулах будем обозначать акцент символом $\dot{\rightarrow}$ .

4.8. Директор

Другим вариантом представить порядок является стрелочка. В ФОРАОН она моделируется как указание на один из полюсов контракта. В отличие от акцента, мы рассматриваем стрелочку как изменяемый объект, т.е. она может быть инвертирована.

Построим объект, называемый директором. Для этого возьмём контракт и надпишем (при помощи акцента) над его базисом выбранное направление. В графической нотации это выражается как на Рис. 7i. Мы будем также использовать обобщённую форму директора для выражения следования (Рис. 7ii).

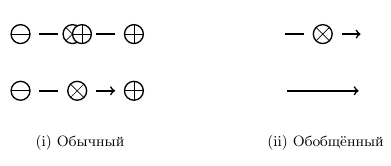
Программная нотация задаёт определение директора как класс director, компонентами которого являются: контракт c и акцент a. Конструктор director() определяет порядок конструирования директора. Функция selected() возвращает выбранное направление, по аналогии с order.

public class director : system {

    public contract c;
    public accent a;

    public director(drn d = drn.p) {
        c = new();
        a = new() { o1 = c.basis, o2 = new[] { c.o1, c.o2 }[(int)d] };
        basis = c.basis; }
    
    public drn selected() => (drn)a.o2.place;
    
    public override system[] parts() => new system[] { c, a, }; }

В формулах будем обозначать директор символом $\mathscr{D}$ или стрелочкой.

4.9. Цепочка

Рассмотрим, как построить объект из двух (или более) контрактов. Будем объединять контракты путём надписывания (акцент) базиса следующего контракта над полюсом предыдущего. Объединяемые контракты изображаются под разными ориентациями (Рис. 8).

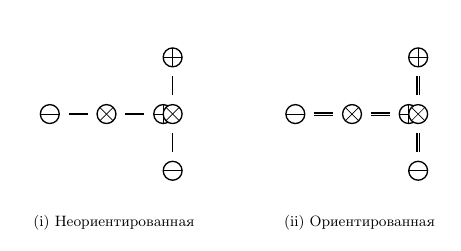
Данный объект будем называть цепочкой и обозначать как $\mathscr{S}$ .

Программная нотация задаёт цепочку как класс sequence. В нём объекты o1 и o2 это первый и второй контракты, размещение которых принимает значения ориентации, первичная и вторичная. Базисом цепочки является базис первого контракта. Элементами цепочки являются контракты и акцент(ы) между ними. Если следующие контракты надписаны только над одним из направлений предыдущих контрактов, такую цепочку назовём линейной, если над каждым, то насыщенной.

public class sequence : discriminator {

    public accent a;
    public sequence() {

        (o1, o2) = (new contract(), new contract());
        (o1.place, o2.place) = (orn.p, orn.s);
        a = new() { o1 = ((contract)o1).o1, o2 = o2.basis };
        basis = o1.basis; }

    public override system[] parts() => new[] { o1, o2, a }; }

4.10. Собственный контур

Определение собственных объектов на C# дано в 3.1. Теперь запишем графическую форму (Рис. 9), которую будем называть собственным контуром.

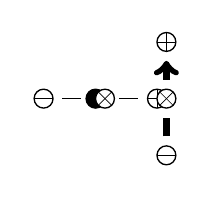
Построение начнём с внимания ("я"). Внимание изображается примитивом, который залит чёрной краской. Поверх внимания записывается смешанная система, которой соответствует контракт, где отрицательный полюс есть память, положительный время.

Для отражения структуры времени используем директор, надписанный над полюсом времени. Коннектор директора маркера выполнен жирной линией. Его полюсы представляют коммутаторы, базис преобразование (transform), выбранное направление действия маркера надписано акцентом над базисом.

4.11. Координаты

Необходимость понятия координат следует из записи начального постулата через свойства плоскости. Действительно, любая надпись на доске находится на некотором месте, а это место может находиться сверху/снизу и/или справа/слева от другого. Формализация понятия места и есть координаты.

Мы можем рассматривать любой объект как абстрагируясь от его координат, так и совместно с ними. В первом случае будем использовать обычную запись , во втором формулу $\mathscr{B} \rightarrow x$ . Данная формула уточняет, что мы рассматриваем объект на доске, где он имеет координаты. В отличие от доски, память маркера содержит всего один объект, и координаты к нему не применимы.

Координатами сложного объекта будем считать координаты его базиса.

5. Темпоральная механика

5.1. Терминология

Под транзакцией будем понимать единичный акт действия маркера, однократное событие исполнения метода function(). Под алгоритмом будем понимать объект, соответствующий полю transform маркера, который описывает изменение аргумента определённым образом в процессе транзакции.

Термином темпоральная механика будем собирательно обозначать части низшей математики, так или иначе относящиеся к понятиям времени и маркера. Темпоральная механика интересуется феноменом и структурой времени, а также поведением объектов в роли алгоритмов.

Традиционная математика не рассматривает напрямую понятие времени, ограничиваясь термином функция [1; с. 712]. Данное понятие оперирует парой множеств, между которыми существует отображение, или закон, который сопоставляет элементы множеств. Таким образом, понятие функции статичное, оно не акцентирует внимание на событии вычисления и его этапах. Но, исходя из начального постулата, игнорировать понятия времени и изменения невозможно, как и временну́ю природу функции.

Состояние действий будем называть моментами времени. С действием связано минимум два момента, первый соответствует начальному состоянию действия, второй его завершённому состоянию.

5.2. Потоки и изоляция

И в физическом, и в абстрактном мире действия могут выполняться как независимо друг от друга, параллельно, так и вслед друг за другом. В последнем случае действия и моменты являются предыдущими/следующими в отношении друг друга.

Область действия терминов "предыдущий/следующий" и "ожидание" будем называть потоком. Следующий момент времени следует за предыдущим только в границах одного потока, т.е. потоки изолированы друг от друга. В рамках математической реальности, потоки соответствуют маркерам.

Если абстрагироваться от цепочки более простых действий внутри маркера, у последнего может быть два состояния: начальное и конечное (выполненное). Сказанное никак не меняется от того, является ли набор действий конечным, бесконечным или несчётным. В отсутствие физического времени, количество действий, необходимых для перехода из начального в конечного состояния, имеет чисто теоретический интерес; следовательно, мы можем просто рассматривать маркер в интересующем нас состоянии.

5.3. Порядок следования

Средства порождения структуры в ФОРАОН диктуют определённые правила следования. Так, базис контракта предшествует полюсам: в его отсутствие полюсы нельзя записать, т.к. их расположение было бы не определено.

Запись объекта начинается с его базиса, что вполне естественно, т.к. это единственный объект, гарантированно присутствующий в записи любой абстракции. При наличии контракта, полюсы записываются вслед за ним. После записи полюсов, появляется возможность надписать один из них над базисом, образуя директор, и/или надписать другие примитивы (контракты) над полюсами. Наконец, после записи всех примитивов, можно записывать выходящие из них стрелочки и следовать по ним.

Таким образом, структура объектов естественным образом образует граф следования примитивов.

5.4. Синхронность и противоречия

Рассмотрим принципиальное отличие операций чтения и записи. Поскольку начало и конец операции отстоят во времени, то при чтении, чтобы получить данные, надо дождаться окончания операции. В отличие от чтения, запись не возвращает данные, поэтому дожидаться завершения не требуется.

Свойство операции ожидать завершения будем называть синхронностью.

Чтение и запись элементов выполняется в порядке следования (см. 5.3). В этой связи необходимо рассмотреть ситуацию, когда обнаруживается, что элемент следует за собой или более чем за одним другим элементом. Подобную ситуацию будем называть противоречием, или коллапсом времени. Она характеризуется тем, что однозначно установить прошлое объекта становится невозможным.

Запись, как асинхронная операция, движется по графу объекта от прошлого к будущему и не возвращается, поэтому она не препятствует занесению в память объектов с противоречиями (в противном случае мы не могли бы о них узнать). Однако чтение, выполняясь синхронно, движется от прошлого к будущему и обратно, поэтому невозможность вернуться по графу следования в однозначное прошлое должна приводить к аварийному завершению операции (исключение). Коллапс времени, в частности, наблюдается при равенстве коммутаторов маркера.

Надо полагать, что загадочная природа парадоксов связана с тем, что противоречивое высказывание может быть формально записано, но не может быть формально прочитано. Без осмысления различий между чтением и записью, данная ситуация воспринималась как нечто неумопостижимое.

5.5. Транзакция

Запишем транзакцию в графической (Рис. 10) и программной нотации.

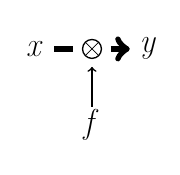
Здесь алгоритм записывается в поле transform маркера, после чего исполняется метод function(). Маркер не содержит ограничений в отношении объектов, которые можно использовать как алгоритм. Так, нет ограничения по дискретности: непрерывные алгоритмы равно допустимы.

На языке C#, эта транзакция сводится к вызову алгоритма :

    dynamic f = ...;
    object x = ...;
    //
    object y = f(x);

Напомним, что мы, в общем случае, характеризуем алгоритмы направлением, положительным или отрицательным (т.е. или ). В некоторых случаях положительный и отрицательный алгоритмы взаимно обратны, в некоторых нет; а для ряда алгоритмов существует только один вариант.

5.6. Пустой алгоритм

В вырожденном случае, алгоритм не вносит никаких изменений. Такой алгоритм будем называть пустым (он необходим в том числе по принципу универсальности). Пустой алгоритм исполняется нуль-системой: $x \equiv \underline{\alpha}(x)$ . Действительно, нуль-система не содержит ни элементов, ни информации, которые могли бы описывать изменение.

5.7. Структурные алгоритмы

Запись новых элементов объекта также называется конструированием. В ФОРАОН объекты имеют явно заданный порядок создания, в процессе которого, подобно зародышу, они проходят стадии более простых объектов. Например, объект сначала является единичным примитивом, затем контрактом, а затем, наконец, директором, в соответствии с графом следования.

Путём использования ластика, можно проводить обратное к конструированию деконструирование. Конструирование и деконструирование относятся к структурным алгоритмам. Другим примером таких алгоритмов являются алгоритмы над множествами (см. 8.3, 8.4).

6. Движения

6.1. Обобщённое движение

Рассмотрим теперь алгоритмы, которые изменяют информационный аспект объекта. Исходя из свойств плоскости и имеющихся дискриминаторов (направления, ориентации, координаты), в наличии два алгоритма: вращение и сдвиг, вместе называемые движениями.

Источником необходимости движений является объединение понятия изменения с понятиями направления, ориентации и координат. Таким образом, движения вытекают из смысла и записи начального постулата. Оба движения характеризуются направлением и величиной; однако поначалу мы будем игнорировать величину, рассматривая некоторое элементарное значение. Сдвиг также имеет ориентацию.

В мнемонической форме движение будем записывать словом "переместить".

Найдём объект, который служит алгоритмом движения. По структуре и информации движение точно соответствует директору, т.е. его результат вычисляется как $y = \mathscr{D}(x)$ . Директоры $\mathscr{D}^+$ или $\mathscr{D}^-$ выполняют вращение (поворот), директоры $\mathscr{D}_p^+$ , $\mathscr{D}_p^-$ , $\mathscr{D}_s^+$ или $\mathscr{D}_s^-$ -- сдвиг.

Примем это представление движения за основу и продолжим рассуждения.

6.2. Пустое движение

Принцип универсальности требует рассмотреть движение, которое не вносит изменений (пустое движение). Отметим, что пустое движение не эквивалентно пустому алгоритму. Последний является более простым понятием: пустое движение всё же является движением.

Модель пустого движения найдём "методом горшочка". Рассмотрим директор. Он представляет собой контракт, над базисом которого надписан один из полюсов. Представим, что контракт -- это горшочек, внутри которого лежит надписанный полюс (контракт выполняет функцию памяти в отношении надписанного полюса). Тогда пустой горшочек -- это контракт, над которым полюс не надписан. Отсюда алгоритм пустого движения есть контракт.

Пустое движение, таким образом, записывается как $x \equiv \underline{\omega}(x)$ ; мнемоническая запись -- "стоп".

6.3. Завершённое движение

Рассмотрим одно движение в заданном направлении вслед за другим. Понятно, что комбинация элементарных движений также представляет собой движение, отличающееся от элементарного только величиной. Структуру такого движения в нотации ФОРАОН выразим цепочкой (Рис. 11i).

В виде формулы такой объект записывается как:

$\mathscr{D}'^+_p \equiv \mathscr{D}^+_p \rightarrow \mathscr{D}^+$

Данная запись, при её логичности, содержит проблему, которую необходимо указать и решить. Суть проблемы -- ввод паразитного смысла. Обозначим директоры как и , а их примитивы как $\underline{\alpha}^0_i,\underline{\alpha}^+_i,\underline{\alpha}^-_i$ . Тогда положительный полюс первого директора имеет формулу $\underline{\alpha}^+_1 \dot{\rightarrow} \underline{\alpha}^0_2$ , в то время как второго записывается как $\underline{\alpha}^+_2$ . Т.к. оба движения абсолютно идентичны, чтобы запись была верной и не содержала непреднамеренно введённого смысла, это различие необходимо устранить.

Для этого надпишем над вторым директором контракт (Рис. 11ii). Получившийся объект в мнемонической форме можно записать как "переместить, переместить, стоп", в формуле -- $\mathscr{D}^+_p \rightarrow \mathscr{D}^+ \rightarrow \underline{\omega}$ , что полностью соответствует смыслу указанного движения, которое будем называть завершённым.

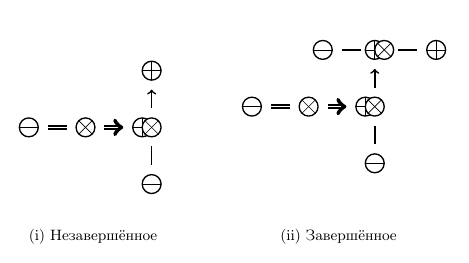
6.4. Неограниченное движение

Рассмотренное выше завершённое движение -- не единственный способ устранить ввод паразитного смысла. Другим способом является применить повторение, как показано на Рис. 12. Здесь прерывистая линия стрелочки означает повторение во времени, т.е. оператор goto. Мнемоническая запись: "переместить, повторить (переместить)". В символическом виде повторение будем записывать как $\mathscr{R}$ . Важно: повтор операции не означает, что объект следует сам за собой.

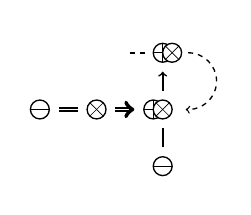
6.5. Редуцированное движение

Формула кратного движения (см. 6.3) задаёт новое движение в форме $a \equiv b \rightarrow b$ , при этом определяемый объект находится в левой части формулы. Перепишем формулу, поменяв элементарное движение и определяемый объект местами:

$\mathscr{D}^+ \equiv \mathscr{D}'^+ \rightarrow \mathscr{D}'^+$

Движение $\mathscr{D}'$ в данной формуле будем называть редуцированным.

На доске выберем (произвольно) некоторую точку "стоп" (). Поместим над ней центр движения (Рис. 13i). Ясно, что точка делит движение пополам.

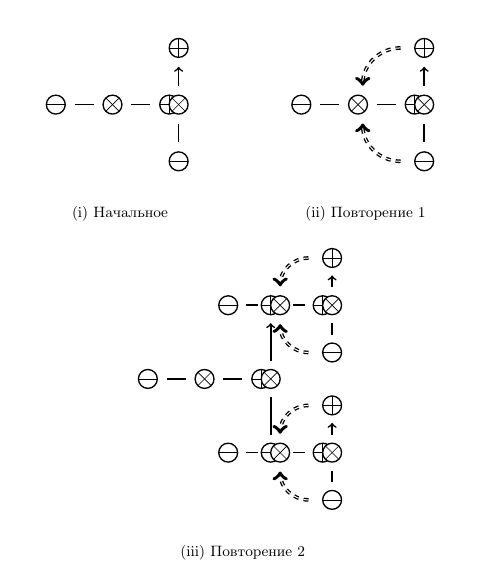
Далее повторим это действие, для чего добавим к объекту две стрелочки (Рис. 12ii). Стрелочки выполнены двойной прерывистой линией, что означает "параллельный goto", т.е. повторы, выполняемые одновременно разными маркерами. Стрелочки предписывают далее разделить движения $\mathscr{D}'$ новыми точками. Поскольку стрелочки являются элементами объекта, при повторе действия они копируются в определение, таким образом, задавая параллельно-рекурсивный алгоритм получения новых движений $\mathscr{D}'', \mathscr{D}''', ...$ , каждое из которых в два раза меньше предыдущего.

С алгоритмом редуцирования связано понятие непрерывности. Действительно, каждый контракт можно разделить на два меньших и так до бесконечности, из-за чего количество компонентов результирующей структуры равна $2^\infty$ , что является признаком континуума.

Непрерывность, т.е. объект со структурой на Рис. 13ii, будем обозначать символом $\mathscr{T}$ .

6.6. Комбинаторика вращения

До настоящего момента наши рассуждения одинаково относились как к вращению, так и к сдвигу. Теперь необходимо указать принципиальное различие между ними.

При повторении сдвига в одном направлении результат никогда не становится равным пустому сдвигу. Это не верно для вращения. Если ориентация вращаемого объекта (например, директора) не рассматривается, то повтор вращения эквивалентен пустому вращению (здесь директор выступает как аргументом, так и алгоритмом транзакции): $\mathscr{D}^+(\mathscr{D}^+) \equiv \mathscr{D}^-$ , $\mathscr{D}^+(\mathscr{D}^-) \equiv \mathscr{D}^+$ .

Если же ориентация рассматривается, то вращение последовательно меняет ориентацию и направления: $\mathscr{D}^+(\mathscr{D}^+_p) \equiv \mathscr{D}^+_s$ , $\mathscr{D}^+(\mathscr{D}^+_s) \equiv \mathscr{D}^-_p$ , $\mathscr{D}^+(\mathscr{D}^-_p) \equiv \mathscr{D}^-_s$ , $\mathscr{D}^+(\mathscr{D}^-_s) \equiv \mathscr{D}^+_p$ , т.е. четыре вращения в одном направлении эквивалентны пустому вращению.

6.7. Свободное движение

Из формул кратного и редуцированного движений следует, что в общем случае движение может быть любой комбинацией кратных и/или редуцированных движений, которая может быть конечной или бесконечной. Движение произвольной величины будем называть свободным.

Ввод свободного вращения говорит о том, что для свободного сдвига, надо заменить фиксированное перечисление orn в качестве ориентации контракта на вещественное число. Тогда значению orn.p будет соответствовать или $\pi$ , а значению orn.s -- $\frac{1}{2}\pi$ или $\frac{3}{2}\pi$ .

7. Математические понятия

Мы ввели необходимые абстракции, составляющие описание математической реальности. Теперь можно связать основные математические понятия с теми или иными структурами ФОРАОН.

7.1. Объект

Само понятие объекта уже обсуждалось в 4.1. Здесь напомним, что в рамках АММ, рассмотрение объекта означает запись его структуры на доске маркером. Наличие описанной структуры или отыскание таковой относит предмет рассуждений к математическим объектам.

Отдельно коснёмся вопроса численных характеристик памяти и объектов. Пример человека показывает, что объём и размерность мозга не ограничивает рассмотрение разумом исчислимых и неисчислимых бесконечностей и объектов любой размерности. Это объясняется тем, что в память записывается не "сам объект" во всей своей полноте, а лишь его структура. То же самое верно и для АММ, где структура записывается на доске.

Присутствие $x(\mathscr{B})$ есть состояние объекта после создания, а отсутствие $\mathscr{E}(x)$ есть его состояние после стирания. Понятие единственности будем ассоциировать со структурой объекта. При оценке структуры необходимо принимать во внимание граф следования, а не линейную цепочку parts().

7.2. Равенство

Необходимость понятия равенства следует из способности мышления оценивать изменения. Проиллюстрируем равенство на следующем примере. Запишем на доске число в двух местах. Единственное, что отличает эти объекты друг от друга, это их координаты, т.е. значение дискриминатора.

Под отличием от будем понимать алгоритм, который преобразует один объект в другой. Если этот алгоритм пуст, т.е. $y = \underline{\alpha}(x)$ , то изменения относительно отсутствуют, что и примем за формальное определение равенства. В данном случае, дискриминаторами выступают не координаты, а сами символические обозначения и .

Известны аксиомы равенства, например $\forall x (x = x)$ или $\forall x \forall y(x = y \Rightarrow y = x)$ [3; с. 113]. Поскольку алгоритм $\underline{\alpha}(x)$ не вносит в изменений, не важно, какова структура , а в случае единственного объекта отсутствует различие даже в дискриминаторах, что доказывает первую аксиому. Если , то различие между ними лишь в обозначениях, т.е. смысл не изменится, если переназвать как и наоборот: так доказываются вторая аксиома.

Помимо равенство, математика использует термин "тождественность", понимая под этим равенство, не зависящее от переменных факторов. Мы будем использовать знак $\equiv$ в смысле сравнения структуры, имея в виду, что отношение может быть переопределено для конкретного вида объектов, например множеств или чисел; так, , но $1+1 \not \equiv 2$ .

Запись $y \equiv x$ будем также прочитывать " в точности является ". Если структура входит в структуру , но последний имеет дополнительные шаги конструирования, то будем говорить, что является , но не в точности. Это отношение будем называть подобием и обозначать как .

Помимо равенства, знак используется для записи присваивания: .

7.3. Существование

Описывая предел осознания (см. 3.1), мы характеризовали "я существую" как указание на собственный характер памяти и времени. Рассмотрим теперь существование для случая абстрактных объектов.

Традиционно поясняется, что объект существует, если его определение не противоречиво. Ранее, в отсутствие способа построить простейшие объекты с нуля, нельзя было проверить их непротиворечивость, которую приходилось принимать на веру.

Описав противоречие, как ситуацию следования объекта за собой или более чем одним другим объектом (коллапс времени, см. 5.4), получаем строгое определение существования. Предъявив определение объекта и показав однозначность следования, мы доказываем его существование.

7.4. Логические значения

В понятие логических значений входит: истина (), ложь () и функция отрицания. Значения и мы полагаем атомарными, они не состоят из частей. Одновременно, они содержат информацию, ровно один бит. То есть, по составу знаний и информации, логические значения эквивалентны полюсам контракта: $T \equiv \underline{\alpha}^+$ , $F \equiv \underline{\alpha}^-$ , отрицание эквивалентно вращению: $\neg(x) = \mathscr{D}(x)$ .

Различия в смысле, делающие истину истиной, а ложь ложью, появляются при вводе функций двух логических аргументов. По числу возможных наборов результатов, имеется всего 16 различных функций, разделённые на 8 пар (алгоритм и его отрицание).

7.5. Числа

По составу знаний и информации и по поведению, число эквивалентно алгоритму сдвига. Действительно, число (кроме нуля) имеет знак, величину (модуль) и угол (аргумент) к оси на комплексной плоскости. Эти элементы соответствуют направлению, величине и ориентации сдвига.

В этой связи, можно отметить следующую терминологию и структуру:

нуль $0 \equiv \underline{\omega}$
единица $1 \equiv \mathscr{D}^+_p \dot{\rightarrow} \underline{\omega}$
мнимая единица $i \equiv \mathscr{D}^+_s \;\dot{\rightarrow}\; \underline{\omega}$
вещественное $\mathbb{R}$ число есть алгоритм сдвига с первичной ориентацией
комплексное число $r e^{i \varphi}$ есть алгоритм сдвига на величину с ориентацией $\varphi$
дискретное число $\mathscr{N}$ есть алгоритм кратного сдвига, см. 6.1
натуральное число $\mathbb{N}$ есть $\mathscr{N}^+_p$
целое число $\mathbb{Z}$ есть дискретное число первичной ориентации $\mathscr{N}_p$ или нуль
натуральная бесконечность $\infty \equiv \mathscr{R}(\mathscr{D}^+_p)$
несчётная бесконечность есть непрерывность $\mathscr{T} \equiv \mathscr{R}^2(\underline{\omega} \;\dot{\rightarrow}\; \mathscr{D}^+)$

Знак числа будем записывать в виде верхнего индекса: $1 \equiv 1^+, -2 \equiv 2^-$ .

Связь определения числа с множествами рассмотрена далее.

Рассмотрим базовые операции над числами, для чего исследуем поведение числа в качестве алгоритма. Вспомним, что сдвиг вытекает из объединения понятий изменения и координаты. Со сдвигом (числом) можно связать координату: если рассматривать сдвиг точки , то величина числа совпадает с координатой конечной точки сдвига. Следовательно, число, действуя как алгоритм над числом, меняет, по аналогии с координатой, величину числа-аргумента.

Рассмотрим транзакцию на Рис. 14.

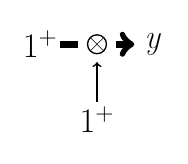
Её алгоритм имеет единственный аргумент, т.е. , что эквивалентно ; в свою очередь, . Отметим, что , а . Алгоритм, симметричный в положительном направлении и асимметричный в отрицательном направлении, является повторяющимся шаблоном, который назовём симметрической парой.

Ранее, отсутствие структуры чисел приводило к необходимости принимать аксиомы о них на веру; например, на вопрос, является ли натуральным числом, не было доказанного ответа. В нашем случае, структура чисел известна, поэтому аксиомы о числах превращаются в доказанные высказывания.

Приведём примеры.

есть натуральное число. Это высказывание следует из определения $\mathbb{N}$ .

Число, следующее за натуральным, тоже является натуральным. Аксиомы Пеано рассматривают функцию следования так же, как и сами натуральные числа: как чёрный ящик. Поскольку функция следования совпадает с , эта аксиома становится доказанным высказыванием.

не следует ни за каким натуральным числом. Исходя из природы функции следования, следует за нулём. Т.к. нуль не входит в определение $\mathbb{N}$ , единица не следует за натуральным числом.

Если натуральное число следует как за числом , так и за числом , то и равны. Если , то обратная функция ; значит, , следовательно, .

8. Множества

8.1. Природа понятия

Математическая энциклопедия [2; с. 758-759] сообщает, что "понятие множества принадлежит к числу первоначальных математических понятий и может быть пояснено только при помощи примеров". По понятным причинам, в случае низшей математики этого недостаточно.

Понятие множества, безусловно, связано с его элементами; но в отношении самих элементов ничего утверждать нельзя: их может не быть вовсе, или быть конечное, бесконечное или даже не счётное количество. Отсюда, природа множества связана не с составом его элементов; но тогда с чем?

Поскольку мы начинаем конструирование объекта с одиночной нуль-системы, множество неминуемо должно конструироваться ранее своих элементов. Данное утверждение, по сути, единственное, что достоверно известно о любом множестве. Иными словами, множество нужно рассматривать как проявление отношения порядка/следования.

Поэтому: в точности множество есть директор $\mathscr{D}$ . Объект, стоящий до стрелочки, будем называть телом множества, объект(ы) после стрелочки суть его элемент(ы), а саму стрелочку назовём маршрутом множества. В простейшем случае (изолированный директор) и тело, и единственный элемент множества есть нуль-система $\underline{\alpha}$ .

По методу горшочка, пустое множество суть контракт: $\varnothing \equiv \underline{\omega}$ .

Отсюда видно, как натуральные числа выражаются через множества: $0 \equiv \varnothing, 1^+ \equiv \{\varnothing\}$ , $2^+ \equiv \{\{\varnothing\}\}, 3^+ \equiv \{\{\{\varnothing\}\}\}$ . Отметим, что данное выражение не является способом построить множество с элементами, как например $2 = \{ \varnothing ,\{ \varnothing \}\}, 3=\{ \varnothing ,\{\varnothing\},\{ \varnothing ,\{ \varnothing \}\}\}$ , и не противоречит этому способу.

8.2. Элементный состав

О множестве можно сказать, что оно выполняет функцию памяти в отношении своих элементов. Об этом говорит то, что множество "содержит" элементы, которые, в свою очередь, могут быть добавлены в него или удалены. Этот факт иллюстрирует процесс возникновения новых видов памяти.

Мы рассмотрели множество с одним элементом. Для построения множества с элементами нужен более сложный маршрут, и примером такого маршрута является натуральное число , где базис -го директора цепочки связан стрелочкой с -м элементом (Рис. 15).

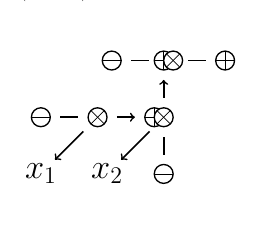
Иным способом записывается несчётное множество (континуум). Здесь телом множества является начальная точка : действительно, знание, где нужно записать сдвиг, предшествует собственно записи сдвига. Отношение следования (маршрут), вместо директора, записано акцентом. За телом следует записанный сдвиг (линия), содержащий в себе все $2^\infty$ точек.

В связи с записью множества, надо отметить тот факт, что и доска, и лента машины Тьюринга упорядочены. По этой причине, любая запись множества также упорядочена. Однако, если рассматривается формирующий множество алгоритм в начальном состоянии, то результат ещё не записан, и маршрута ещё нет; есть лишь намерение в отношении состава элементов. По этой причине, множества по умолчанию рассматриваются как неупорядоченные.

Запись $\{x_1,x_2\}$ означает пустое тело, т.е. эквивалентна $\underline{\alpha} \rightarrow \{x_1,x_2\}$ .

Рассмотрим универсум, т.е. множество всех объектов. В обычном понимании, такое множество не должно существовать, т.к. следует само за собой. Низшая математика позволяет разрешить это противоречие. Любой объект, если он рассматривается, расположен в памяти. Следовательно, в качестве коллекции всех объектов естественным образом выступает память $\mathscr{B}$ как таковая. Поскольку память является не абстрактным, а собственным объектом, её существование следует из начального постулата. Поэтому, хотя память и не содержит саму себя, она содержит все абстрактные объекты.

8.3. Алгоритмы

Подобно доске, где объект может быть записан или стёрт под воздействием маркера, элемент может быть добавлен в множество или удалён из него. Добавление элемента в множество будем записывать как $A \oplus x$ , удаление как $A \ominus x$ . Если объект присутствует (отсутствует) в множестве, то добавление (удаление) не изменяет это множество, поэтому $A \oplus x$ и $A \ominus x$ не являются взаимно обратными.

Пусть и -- множества. Рассмотрим алгоритмы и . Применение множества к множеству в положительном направлении добавляет все элементы к , а в обратном направлении удаляет все элементы из . Запишем сказанное в виде формул (8.1) и (8.2). Здесь запись $(f) \rightarrow a$ будем читать как "выполнить действие и положить как результат". Запись $\forall x \in A (f(x))$ будем читать как "для каждого элемента из выполнить действие ".

(8.1)

$\begin{split} B^+(A) \equiv (&C = A \\ & \forall x \in B (C \oplus x)) \rightarrow C \end{split}$

(8.2)

$\begin{split} B^-(A) \equiv (&C = A \\ & \forall x \in B (C \ominus x)) \rightarrow C \end{split}$

Более привычная бинарная форма записи этих алгоритмов выглядит как объединение $A\cup B$ и разность $A\setminus B$ . Видно, что эти алгоритмы образуют симметрическую пару. Отметим, что данные операции не являются взаимно обратными.

Дополнение множества выразим как $\overline{A} \equiv A^-(\mathscr{B})$ .

Перейдём к алгоритмам двух аргументов. Простейшими из них являются пересечение $A \cap B$ (8.3) и симметрическая разность $A \bigtriangleup B$ (8.4). Данные алгоритмы устроены аналогично: на основе $\oplus$ и $\ominus$ , соответственно. Запись $a(x) \Rightarrow f(x)$ в данном контексте будем читать как "если функция истинна, то выполнить действие ".

(8.3)

$\begin{split} A \cap B &\equiv (C = B^+(A)\\ &\quad \; \; \; D = \varnothing\\ &\quad \; \; \; \forall x \in C ((x \in A \land x \in B) \Rightarrow D \oplus x )) \rightarrow D \end{split}$

(8.4)

$\begin{split} A \bigtriangleup B &\equiv (C = B^+(A)\\ &\quad \; \; \; \forall x \in C ((x \in A \land x \in B) \Rightarrow C \ominus x )) \rightarrow C \end{split}$

Нам понадобится условие равенства множеств , поэтому зададим его строго формулой (8.5).

(8.5)

$\begin{split} (A = B) & \equiv (C= A,D= B \\ &\quad \; \; \; \forall x \in A (D \ominus x) \\ &\quad \; \; \; \forall x \in B (C \ominus x)) \rightarrow (C \equiv \varnothing \land D \equiv \varnothing) \end{split}$

Остальные алгоритмы над множествами распадаются на перечисленные выше более простые.

8.4. Аксиомы теории множеств

Описав структуру и поведение множеств, обнаруживаем, что аксиомы о них могут быть доказаны. Проиллюстрируем это на примерах (формулировка аксиом по [3; с. 126]).

Аксиома объёмности. Любые два множества и , содержащие одни и те же элементы, равны: $\forall x \forall y(\forall z (z \in x \equiv z \in y) \Rightarrow x=y)$ . В соответствии с формулой (8.5), в этом случае между множествами отсутствуют относительные изменения, что эквивалентно равенству.

Аксиома пустого множества. Существует множество $\varnothing$ , не содержащее элементов: $\exists \varnothing \forall y (y \notin \varnothing)$ . Истинно по определению: $\varnothing \equiv \underline{\omega}$ .

Аксиома пары. Для любых множеств и существует множество , содержащее в точности элементы и : $\forall x \forall y \exists z \forall w(w \in z \equiv (w=x \lor w = y))$ . Запишем транзакцию:

$\begin{split} z = ( & A= \varnothing \\ & A \oplus x \\ & A \oplus y ) \rightarrow A \end{split}$

Данная формула непротиворечиво определяет , следовательно существует.

Аксиома объединения (суммы). Для любого семейства множеств существует множество , элементами которого являются в точности элементы множеств, принадлежащих : $\forall x \exists u \forall y(y \in u \equiv \exists z(z \in x \land y \in z))$ . Запишем транзакцию:

$\begin{split} u = ( & A= \varnothing \\ & \forall B \in x (\forall i \in B(A \oplus i))) \rightarrow A \end{split}$

Данная формула непротиворечиво определяет , следовательно, существует.

Аксиома множества всех подмножеств. Для любого множества существует множество , элементами которого являются все подмножества множества x и только они: $\forall x \exists y \forall z(z \in y \equiv z \subseteq x)$ . Найдём способ вычисления . Зададим некоторое множество и парный к нему рекурсивный алгоритм $\Delta_A$ :

$\begin{split} \Delta_A(a) \equiv ( \forall i \in a (&B = a\\ & B \ominus i \\ & B \not\equiv \varnothing \Rightarrow A \oplus B \\ & \Delta_A(B))) \end{split}$

Тогда транзакция вычисления запишется как:

$\begin{split} y = (&A = \varnothing \\ & \Delta_A(x)) \rightarrow A \end{split}$

Эта формула непротиворечиво определяет , следовательно существует.

Схема аксиом выделения. Для любого множества существует множество , содержащее в точности элементы множества , которые выполняют условие :
$\forall \forall \;\forall x \exists y \forall z(z \in y \equiv(z \in x \land A(z)))$ . Запишем транзакцию:

$\begin{split} y = ( & B= \varnothing \\ & \forall i \in x (A(i) \Rightarrow B \oplus i)) \rightarrow B \end{split}$

Данная формула непротиворечиво определяет , следовательно существует.

9. Заключение

Новизна и идеологическая основа данной работы -- введение формальной модели мышления в пространство математики. Данный приём позволил предъявить структуру основных математических объектов, ранее задававшихся только аксиоматически, и описать их поведение. Также обнаружилось, что эти объекты входят друг в друга как элементы, в порядке увеличения сложности:

нуль-система $\underline{\alpha}$
контракт $\underline{\omega}$ (логические значения, нуль, пустое множество)
директор $\mathscr{D}$ (множества)
цепочка $\mathscr{D} \rightarrow \underline{\omega}$ (числа)

Существенно, что данная иерархия не придумана, а обнаружена посредством анализа самодоказывающего высказывания -- начального постулата. Если ранее этот тезис был предметом преимущественно философской дискуссии, то анализ его записи, наряду со смыслом, делает его исчерпывающим источником математического знания, потенциал которого демонстрирует статья. Универсальный, структурированный язык обеспечивает надлежащую формализацию любых знаний, с явной передачей смысла без потерь.

Помимо чисто математических результатов, статья позволяет строго представить смысл математического знания в системах искусственного интеллекта. Если человек приходит к пониманию числа как "объекта, возникающего в процессе счёта" постепенно, в процессе опыта, то система на базе АММ может иметь идеи числа, множества и др. понятными уже на базовом уровне своей конструкции. Также АММ содержит абстракции, требуемые для осознания системой ИИ самой себя.

Список литературы

[1] Математическая энциклопедия, 5, Советская энциклопедия, Москва, 1982.

[2] Математическая энциклопедия, 3, Советская энциклопедия, Москва, 1982.

[3] А. С. Герасимов, Курс математической логики и теории вычислимости: учебное пособие. 3-е изд., испр. и доп., ЛЕМА, С-Петербург, 2011.

30.07.2023

Самойлов Андрей Владимирович (Andrei Samoylov)
Email: as@mixed.systems

PDF-версия доступна здесь.

Комментарии (150)

Ramayasket Автор
30.07.2023 21:32
#0
+1
Итак, прошло 15 часов с момента публикации. Надо отдать должное @olegchir: он точно знал, что будет. Весь день отвечаю на комментарии, и уже можно указать на ряд общих моментов.

Популярный modus operandi:
- Прочитать несколько начальных разделов
- Прочитанное дополнить своими додумками
- Остальное проигнорировать (цитата - "лень")
- Полученную проекцию статьи объявить "бредом" (цитата) -- самое смешное, вполне заслуженно, ибо к содержанию статьи такая проекция не имеет никакого отношения
В этой связи надо уточнить вот что.

Все выводы в статье ПРОВЕРЯЕМЫ. Для всех объектов указана цепочка обоснования, структура и информация. Если вы видите необходимость дискуссии, ПОЖАЛУЙСТА, прочитайте статью до конца. Оцените выводы. При написании возражений, указывайте конкретную цепочку рассуждений и то место в ней, с которым вы не согласны.

ИМХО, такой способ беседы будет куда продуктивнее. Спасибо.

P.S. Примите во внимание, что статья не относится к написанию ИИ, не рассматривает работу мозга или работу физических компьютеров.

Tzimie
30.07.2023 21:32
#25805474
Чем хорош arxiv.org, это наличием abstract. Вы можете сформулировать основную идею в одном абзаце?

В PDF у вас "рассматривается ...". Ну рассматривается, а идея то в чем?

Человеческое мышление бесконечно далеко от формализмов и эволюционно произошло от мышления животных, которое по своей сути нематематическое. В основном мы думаем эмоциями.
1. Ramayasket Автор
  30.07.2023 21:32
  #25805524
  +1
  1) В русскоязычных публикациях Abstract называется Аннотация. В начале статьи.
  
  2) Как же мы эмоциями додумались до математики? Или вы думаете что теоремы доказываются эмоциями?
  1. Tzimie
    30.07.2023 21:32
    #25805534
    2. Но уж точно они не доказываются формальными системами вывода, а какими то непонятными эвристиками. И потом вызывают эмоции (this proof is from THE BOOK (c) Пол Эрдош)
    
    Ramayasket Автор
    30.07.2023 21:32
    #25805542
    уж точно они не доказываются формальными системами вывода
    
    Посмотрите пункт [3] библиографии -- там как раз описываются формальные теории и доказательства.

Tzimie
30.07.2023 21:32
#25805500
+6
Мне очень не хочется критиковать, потому что тема мышления редко освещается здесь (и hard problem of consciousness, которая с этим вероятно связана)

Однако (пожалуйста не обижайтесь) пока это выглядит как наукообразное умничание. Как если бы вместо "я поехал на дачу" я бы сказал " я изменил координаты XYZ своего физического тела B так, что евклидово расстояние до дачи D стало равно нулю"

Там не менее буду ждать продолжения
1. Ramayasket Автор
  30.07.2023 21:32
  #25805516
  +2
  То, что вы описываете -- называется формализация. Ваша фраза выглядит как условие задачи по физике. Но ценность формализации не в ней самой, а в результатах.
  1. Tzimie
    30.07.2023 21:32
    #25805558
    А каковы результаты?
    
    Ramayasket Автор
    30.07.2023 21:32
    #25805566
    +1
    Разве об этом не говорится в самом начале? Структура основных математических объектов, имеющая общее дерево наследования. Для начала. И все следствия из этого: точные определения равенства, существования, и далее, чтобы не повторять всю статью. Обо всём этом говорится не завуалированно, а явно и проверяемо.
    
    Вы точно всё прочитали?
    
    Tzimie
    30.07.2023 21:32
    #25806680
    А что из этого не умеет делать ZFC?
    
    Ramayasket Автор
    30.07.2023 21:32
    #25806862
    ZFC это система аксиом. В рамках традиционной математики они не доказываются.
    
    Tzimie
    30.07.2023 21:32
    #25806892
    Я это знаю. Вопрос, что может ваша система что не может делать ZFC.
    
    Честно говоря, я не вижу примера, где при применении вашей системы что-то стало вдруг просто, ясно, или открылось то, что до этого было неизвестно
    
    Вас спросили про табуретку и стол, но вы ушли от ответа
    
    Ramayasket Автор
    30.07.2023 21:32
    #25806904
    +1
    что может ваша система что не может делать ZFC
    
    В описываемой системе аксиомы множеств доказываются. Вы до конца прочитали?
    
    Вас спросили про табуретку и стол, но вы ушли от ответа
    
    Описывать табуретку и стол в терминах ФОРАОН -- это то же самое, что описывать их через квантовую механику. Она по-прежнему там, но табуретка и стол просто слишком сложные объекты для такого описания.
1. victor_1212
  30.07.2023 21:32
  #25805746
  +1
  смотрите что получается на примере -
  
  "Тройку $\{m,t,x\}$ будем называть смешанной системой (англ. mixed system), где память обозначена как , время как , а объекты в памяти как
  
  " На другом конце шкалы сложности находится мозг человека и знания. Нейроны выполняют роль памяти, а нервные импульсы роль времени. Отсюда происхождение термина "смешанная" система, которая состоит как из материальных (нейроны, импульсы), так и из абстрактных (знания) элементов. "
  
  или
  
  "Так, одну из самых простых образуют кварки и глюоны. Действительно, кварки хранят цвет, а глюоны его меняют; таким образом, кварки играют роль памяти, глюоны роль времени, "
  
  Вы пишите так как будто нет разницы между реальным временем и нервными импульсами, или глюонами "играющими роль времени", в этом нет логики, есть только связь по ассоциации, заметим в статье такой прием используется многократно, поэтому получается не построение строгой логичной теории, а имитация, если что прошу извинить за откровенность
  1. Ramayasket Автор
    30.07.2023 21:32
    #25805800
    Нервные импульсы, процессов в ЭВМ, глюоны -- всё это можно было бы назвать какими-нибудь "временны́ми агентами", но решено было оставить просто "время".
    
    Маркер это время математической реальности, тогда как импульсы -- это время мозга. Термин "время" надо воспринимать абстрактно, в статье особо указывается, что речь о физическом времени не идёт.
    
    victor_1212
    30.07.2023 21:32
    #25808166
    > Маркер это время математической реальности, тогда как импульсы -- это время мозга. Термин "время" надо воспринимать абстрактно, в статье особо указывается, что речь о физическом времени не идёт.
    
    смотрите, Вы типа наступаете на те же самые грабли -
    
    сам термин "математической реальности" уже внутренне противоречив, нет такой реальности - математика это абстракция, например абсолютно прямой линии нулевой толщины в природе не существует,
    
    если хотите логичного построения, начните с корректного определения своей абстрактной модели, например построенной на аксиомах,
    
    заметим как только Вы говорите например о виртуальном времени, маркерах и пр. Вы строите свою виртуальную вселенную по платону, которая к реальному физическому миру прямого отношения не имеет, это тоже может быть интересно, но должно быть сделано корректно и логически непротиворечиво, например если хотите определить множество желательно указать предикат, который может быть использован для установления принадлежности к этому множеству и т.д., без этого определение типа -
    
    " Тройку $\{m,t,x\}$ будем называть смешанной системой (англ. mixed system), где память обозначена как , время как , а объекты в памяти как . "
    
    совершенно непонятно, потому что ни память, ни время корректно не определены в рамках той логической системы которую Вы пытаетесь построить, очевидно все три элемента этой тройки являются абстракциями, но абстракциями неопределенными, т.к. неясно к каким именно множествам они принадлежат, и какими абстрактными свойствами обладают
    
    Ramayasket Автор
    30.07.2023 21:32
    #25808370
    сам термин "математической реальности" уже внутренне противоречив
    
    Факт, что вы, не дочитав, стали писать комментарий. Т.к. математическая реальность -- это смешанная система из доски и маркера. А не то, что вы додумали.
    
    начните с корректного определения своей абстрактной модели, например построенной на аксиомах
    
    Использовать новые аксиомы, чтобы доказать старые -- зачем? Если задача решается без новых аксиом.
    
    victor_1212
    30.07.2023 21:32
    #25809030
    +3
    > Факт, что вы, не дочитав, стали писать комментарий. Т.к. математическая реальность -- это смешанная система из доски и маркера. А не то, что вы додумали.
    
    мне ничего не надо додумывать, все Вами уже написано, "математическая реальность" это бессмысленный термин, ровно как и "смешанная система из доски и маркера", они просто не определены в точном математическом смысле, конечно всегда можно сказать что Вас неправильно поняли, не дочитали до конца, не это имелось в виду и т.д., но может быть не стоит этого делать, Вас поняли и прочитали, никакая задача Вами не решена, но если сами не видите недостатки Вашей статьи типа жизнь всегда научит, например отправьте в какой-нибудь приличный журнал, увидите что получится, желаю успеха
  1. flancer
    30.07.2023 21:32
    #25806252
    +2
    В реальном мире абстрактного времени (времени, не привязанного к материи) не существует. Время - это всегда изменение материи. Если ничего не меняется, то ничего и не происходит. Время пропадает. Для измерения времени нам нужен некий метроном - физический процесс с самой высокой частотой из всех наблюдаемых процессов. В компьютерах - это генератор тактовой частоты. В виртуальном мире, созданном компьютером, ничего не может происходить быстрее, чем за один "тик". И не важно, сколько секунд (периодов излучения, соответствующих переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133 при отсутствии возмущения внешними полями) прошло за это "время" в нашем физическом мире. Мы можем остановить генератор в компьютере на несколько секунд и запустить его вновь - вирутальные персонажи внутри не смогут это определить никоим образом. Их "время" было непрерывным всё время. Вполне возможно, что с точки зрения внешнего, более "высокочастотного", наблюдателя за нашим миром атом цезия-133 меняет своё состояние очень даже наравномерно - процесс то ускоряется, то замедляется. Но сами мы этого почуствовать не можем - в нашем физическом мире наш генератор тактовой частоты работает так, что 9 192 631 770 периодов излучения атома цезия-133 всегда равны в точности одной секунде.
    
    Поэтому нет принципиальной разницы между нервными импульсами, изменяющими состояние нейрона, и глюонами, изменяющими состояние кварка (его цвет). Потому что в физическом мире времени в отрыве от материи не существует. Абстрактно можно было бы обойтись и без материи, но не без изменений. Чтобы "время" было, "что-то", пусть и абстактное, обязательно должно меняться. Причём регулярно.
    
    Ramayasket Автор
    30.07.2023 21:32
    #25806266
    Абстрактного времени (времени, не привязанного к материи) не существует
    
    В математике мы можем рассмотреть абстрактную модель физического времени. И получится абстрактное время -- маркер. Конечно существует. В воображении. Абстрактное время меняет абстрактные объекты. Или вы хотите их менять физическим временем?!
    
    KyHTEP
    30.07.2023 21:32
    #25806304
    +2
    Физическое "время" - это мера скорости изменения состояния относительно эталона (смотрим определение 1 секунды в палате мер и весов).
    
    Если у вас есть изменение состояния относительно эталона (тактовой частоты), то у вас модель "физического" времени, что уже само по себе является абстракцией, как и любая другая модель )
    
    Ramayasket Автор
    30.07.2023 21:32
    #25806316
    Действительно, попробуйте-ка построить множество всех натуральных чисел в физическом времени. А в математике -- пожалуйста.
    
    KyHTEP
    30.07.2023 21:32
    #25806330
    А вы пока опишите запах резьбы )
    
    А если серьезно, у множества есть изменение состояния? Только при наличи этого свойства, можно говорить о времени.
    
    Ramayasket Автор
    30.07.2023 21:32
    #25806332
    Добавление элемента в множество -- не изменение его состояния? Об этом, кстати, явно говорится в статье. Видимо, вы до этого не дочитали?
    
    KyHTEP
    30.07.2023 21:32
    #25806338
    А вы про это. Введите минимальную частоту добавления в множество и будет вам время.
    
    Ramayasket Автор
    30.07.2023 21:32
    #25806346
    Вы упорно пытаетесь найти аналогию с физическим временем, которое "течёт и течёт без остановки". Маркер совершает действия по воле математика, тогда и так часто, как нужно. Нужен один раз -- будет один раз, и никакой частоты.
    
    KyHTEP
    30.07.2023 21:32
    #25806362
    +1
    Нет никакой аналогии с физическим временем, т.к. его (времени в бытовом понимании чего-то текущего) не существует.
    А есть скорость изменения состояний, что в чистом виде математическая абстракция.
    
    Вы не можете что-то измерять без эталона.
    
    Даже если будет воля математика, то она будет подвержена некой минимальной частоте физического существования математика. Если это будет программа, то минимальная частота будет частотой cpu.
    
    Приведите пример, где не будет понятия частоты.
    
    Ramayasket Автор
    30.07.2023 21:32
    #25806374
    Приведите пример, где не будет понятия частоты.
    
    Машина Тьюринга
    
    KyHTEP
    30.07.2023 21:32
    #25806384
    Даже если частоты подачи команд явно не указана в описании, то она есть при конкретной реализации, что нужно учитывать.
    
    Есть возможность что-то подать куда-либо больше одного раза, автоматически есть частота (вопрос измеримости ставится отдельно).
    
    В вашем случае (если я правильно понял концепцию маркера) это кол-во изменений в единицу маркера.
    
    Ramayasket Автор
    30.07.2023 21:32
    #25806404
    Конкретная реализация -- это уже переход в физический мир. Мы говорим об абстрактных, воображаемых вещах.
    
    Если маркер выполняет дискретную последовательность действий, то частота, в рамках этой последовательности, по определению 1. А если непрерывную последовательность? Там частоты вообще нет.
    
    KyHTEP
    30.07.2023 21:32
    #25806426
    Конкретная реализация -- это уже переход в физический мир.
    
    А параметры для конкретной реализации - это всё ещё модель. Параметр частоты подачи команд существует по факту наличия подачи команд больше одной.
    
    Если маркер выполняет дискретную последовательность действий, то частота, в рамках этой последовательности, по определению 1
    
    А в ваших терминах времени как его (время) померять для этой последовательности? А то вы уходите в ту часть, где никакого времени нет, "ни вашего ни нашего".
    
    Я напомню, что мы разговариваем о наличи разности между вашим абстрактным времени и так называемым физическим временем.
    Я озвучиваю мысль, что 1) разницы нет 2) почему ее нет
    
    А если непрерывную последовательность? Там частоты вообще нет.
    
    Дискретная последовательность действий и непрерываная последовательность действий - это одно и тоже, т.к. последовательность действий дискретна по определению. Действие - атомарно.
    
    Ramayasket Автор
    30.07.2023 21:32
    #25806434
    Дискретная последовательность действий и непрерываная последовательность действий - это одно и тоже
    
    Попробуйте дискретно выполнить последовательность действий "для каждой точки отрезка" -- там же несчётное множество, какая может быть дискретная последовательность?!
    
    Такое действие даже на машине Тьюринга выполнить нельзя, т.к. она дискретная.
    
    KyHTEP
    30.07.2023 21:32
    #25806454
    +1
    Попробуйте дискретно выполнить последовательность действий "для каждой точки отрезка"
    
    Так действие какое надо соврешить? Вы же у себя в модели описываете единицу действия? Вот и приводите в пример одно действие, а не то, что я сам должен додумать.
    
    Вы уходите в общую математику, а я остаюсь в рамках вашей модели и ваших рассуждений. Привидите пример в вашей lower math непрерывной последовательности действий.
    
    Так-то я могу и бесконечность привести, как пример, математической абстракции вне физического мира или идеальной прямой. Но вы же строите модель (абстракцию) для описания физического явления - мышления.
    
    Ramayasket Автор
    30.07.2023 21:32
    #25806462
    Но вы же строите модель (абстракцию) для описания физического явления - мышления.
    
    Вот здесь вы ошибаетесь. Описания физического явления здесь никакого нет. Статья чисто математическая, мышление присутствует в ней только в виде абстрактной модели -- математической реальности.
    
    KyHTEP
    30.07.2023 21:32
    #25806478
    А можете описать концепцию чисел оставаясь в рамках математической реальности? Без вот этих счетных палочек и яблок.
    
    мышление присутствует в ней только в виде абстрактной модели -- математической реальности
    
    Осталось ответить на вопрос, откуда вы взяли термин "мышление" )
    
    Ramayasket Автор
    30.07.2023 21:32
    #25806488
    А можете описать концепцию чисел оставаясь в рамках математической реальности?
    
    Конечно! Число -- это алгоритм сдвига.
    
    Осталось ответить на вопрос, откуда вы взяли термин "мышление"
    
    Из выражения я мыслю, следовательно, существую, или cogito, ergo sum.
    
    KyHTEP
    30.07.2023 21:32
    #25806512
    Число -- это алгоритм сдвига.
    
    Понятно, а яйцо - это яишница. Вы серьезно не понимаете, что в понятии алгоритма уже есть много математических концепций, и вы не можете это брать за базовый элемент?
    
    Из выражения я мыслю, следовательно, существую, или cogito, ergo sum
    
    Очень математично )
    
    Ramayasket Автор
    30.07.2023 21:32
    #25806554
    1) По поводу алгоритмов действительно сказано много, но это не отменяет того факта, что алгоритм есть описание изменений. И отчего же нельзя использовать этот факт?
    
    2) Данное выражение несёт в себе математическую модель, особенно если обратить внимание на запись этой фразы на доске.
    
    KyHTEP
    30.07.2023 21:32
    #25806596
    +1
    И отчего же нельзя использовать этот факт?
    
    От того, что для описания базовых вещей не используют составные вещи. Иначе получается рекурсия.
    
    Данное выражение несёт в себе математическую модель
    
    Данное выражение действительно несет связь между мышлением и существованием (при этом весьма спорную), но построено на лингвистической модели образов-слов.
    
    Я же у вас спросил про тремин "мышление", как вы это понимаете. А не спорные цитаты из прошлого.
    
    Если вы реально строите модель исходя из понимания данной цитаты, то все вопросы у меня снимаются.
    
    Ramayasket Автор
    30.07.2023 21:32
    #25806622
    Иначе получается рекурсия
    
    Определение алгоритма не ссылается на себя. Рекурсии нет.
    
    Если вы реально строите модель исходя из понимания данной цитаты
    
    В работе же ясно написано -- мы анализируем не только смысл данной фразы, но и её запись на доске.
    
    тремин "мышление", как вы это понимаете
    
    об этом тоже написано. мышление - это смешанная система, причём доска и маркер являются моделью памяти и времени.
    
    KyHTEP
    30.07.2023 21:32
    #25806640
    Определение алгоритма не ссылается на себя. Рекурсии нет.
    
    Число - это алгоритм сдвига, алгоритм - это что-то про шаги, количество шагов - это что-то про числа, число - это алог.... ой
    
    В работе же ясно написано -- мы анализируем не только смысл данной фразы, но и её запись на доске.
    
    Описания физического явления здесь никакого нет. Статья чисто математическая, мышление присутствует в ней только в виде абстрактной модели -- математической реальности.
    
    Сможете эти две ваши взаимоисключающие фразы "подружить"?
    
    Ramayasket Автор
    30.07.2023 21:32
    #25806652
    алгоритм - это что-то про шаги, количество шагов - это что-то про числа
    
    Для определения того, что такое алгоритм, не используется понятие шагов, а тем более их количество. Это можно уже отдельно расписывать. Но в определении рекурсии нет.
    
    Вам нужна большая тщательность в выводах.
    
    Сможете эти две ваши взаимоисключающие фразы "подружить"?
    
    Физические аспекты мышления не рассматриваются, кроме указания на то, что мозг -- это смешанная система. Статья оперирует только абстрактным образом мышления.
    
    KyHTEP
    30.07.2023 21:32
    #25806676
    +1
    Для определения того, что такое алгоритм, не используется понятие шагов, а тем более их количество.
    
    Алгори́тм (лат. algorithmi — от имени среднеазиатского математика Аль-Хорезми [1]) — совокупность точно заданных правил решения некоторого класса задач или набор инструкций, описывающих порядок действий исполнителя для решения определённой задачи.
    
    "шаг" и "порядок действий" точно не одно и тоже?
    
    набор инструкций - про количество
    совокупность точно заданных правил - про количество
    порядок действий исполнителя - про количество
    
    Вам нужна большая тщательность в выводах.
    
    Вы проигнорировали вопрос про две ваших взаимоисключащих фразы.
    
    Ramayasket Автор
    30.07.2023 21:32
    #25806694
    +1
    про количество
    
    В определении алгоритма, которое вы привели, нет слова "количество". Соответственно, нет и рекурсии. Так можно договориться до того, что признать рекурсивным классическое описание множества. Примерно так:
    
    "Множество -- это коллекция элементов. Коллекция -- это про количество. Количество это про числа. Числа выражаются через множества". Видите?
    
    Вы проигнорировали вопрос про две ваших взаимоисключащих фразы
    
    Просто не сразу понял, где взаимоисключение. Но его там и нет. Запись на доске -- имеется в виду тоже абстракция. Записать можно на доске, на бумаге, на экране, да хоть на собственном теле. Общее для всего этого -- абстрактная модель доски.
    
    KyHTEP
    30.07.2023 21:32
    #25806718
    Вы уходите от начальных рассуждений. Я вам напомню
    
    Я: Опишите число без физических сущностей, чисто математикой
    Вы: Число - это алгоритм сдвига
    
    Я: Нельзя использовать составные объекты для описания примитивов иначе рекурсия
    Вы: Описание алгоритма не ссылается на само себя (вот здесь уже пошла манипуляция, т.к. я не говорил что описание алгоритма ссылается на само себя)
    
    Я: (показываю рекурсию при объяснении в кратком виде) Число - это алгоритм сдвига (какие то рассуждения) алгоритм - это что-то про шаги (какие то рассуждения) количество шагов - это что-то про числа (какие то рассуждения) число - это алгоритм сдвига (попробуйте сам объяснить)
    Вы: Для определения того, что такое алгоритм, не используется понятие шагов, а тем более их количество (т.е. вы уже остаетесь в логике своей манипуляции выше, я не говорил про само определение алгоритма, я говорил про цепочку объяснений)
    
    Я: (привожу определенире алгоритма и показываю, что концепция количества прошита в определение и дальше, чтобы ответить на вопрос "что такое количество" нам нужно понятие "числа"
    Вы: В определении алгоритма, которое вы привели, нет слова "количество". Соответственно, нет и рекурсии. (вы уже четко стоите на своей манипуляции, что мы говорим об определении алгоритма, а не о том, что если разбирать по частям, чтобы четко формализовать объект, будет рекурсия, поэтому для описания простых объектов нельзя использовать составные, содержащие внутри простые)
    
    Ramayasket Автор
    30.07.2023 21:32
    #25806742
    +1
    Ещё раз, определение алгоритма не ссылается на числа. "Это про ..." не является частью определения. Таким образом, определение алгоритма не рекурсивно. Оно не ссылается на себя ни напрямую, ни косвенно через числа.
    
    Найдите в определении алгоритма слово "число". Числа можно дописать сбоку многих вещей, но именно сбоку.
    
    KyHTEP
    30.07.2023 21:32
    #25806746
    Я вам буквально показал, что ссылается. Ну на данном этапе отрицания смысла не вижу продолжать.
    
    flancer
    30.07.2023 21:32
    #25806728
    есть ещё вопрос, почему "совокупность" или "набор" не подразумевает "количество"?
    
    Числа выражаются через множества
    
    IMHO, наоборот - множества выражаются через числа: Множество -> коллекция, коллекция -> количество, количество -> числа = Множество ---> числа
    
    В одном множестве X элементов, в другом - Y. Вполне себе выражение, как по мне.
    
    Ramayasket Автор
    30.07.2023 21:32
    #25806790
    +1
    Нет-нет, множества это более простой объект чем числа. Хоть в традиционной математике, хоть в низшей.
    
    Здесь надо уточнить, что такое "выражается через". Это означает структуру, в то время как число элементов и их расположение -- это информация. Почитайте раздел 4.3 "Дискриминаторы".
    
    KyHTEP
    30.07.2023 21:32
    #25806732
    +1
    . Запись на доске -- имеется в виду тоже абстракция. Записать можно на доске, на бумаге, на экране, да хоть на собственном теле. Общее для всего этого -- абстрактная модель доски.
    
    А доска - это что такое в математике, какой объект? А экран? А бумага?
    Т.е. по этому критерию, вы используете абстрактное физическое время. О чем я сразу и сказал )
    
    Ramayasket Автор
    30.07.2023 21:32
    #25806764
    А доска - это что такое в математике, какой объект?
    
    См. п. 3.2 "Доска". Там вся математика приведена.
    
    вы используете абстрактное физическое время
    
    "Абстрактное физическое" это как?
    
    KyHTEP
    30.07.2023 21:32
    #25806768
    "Абстрактное физическое" это как?
    
    См. п. 3.2 "Доска". Там вся математика приведена.
    
    flancer
    30.07.2023 21:32
    #25806556
    А существует ли само понятие "время" применительно к Машние Тьюринга? "Алгоритм завершился за Х шагов". Это "время" или "расстояние"? Если "время", то шаг - это и есть самый высокочастотный процесс в Машине, относительно которого можно измерять всё остальное. Если "расстояние", то времени в самой Машине Тьюринга нет. Паровая и электронная Машины Тьюринга решат один и тот же алгоритм за одно и то же количество шагов. Хотя интуитивно понятно, что электронная должна быть "быстрее" паровой.
    
    Ramayasket Автор
    30.07.2023 21:32
    #25806568
    "Выполнение" шага/шагов это и есть признак времени, хотя в описании машины Тьюринга этот термин не используется.
    
    Но эту машину я привёл в комментариях для примера, почитайте п. 2.3, почему она не подходит как модель памяти/времени.
    
    "Паровая или электронная" -- это уже физическая реализация, она нас не интересует.
    
    Кроме того, машина Тьюринга не может выполнять непрерывные алгоритмы, а мышление может.
    
    flancer
    30.07.2023 21:32
    #25806696
    Я перечитал ещё раз главу 2.3. Вы исключили Машину Тьюринга из-за того, что "лента не даёт возможность представлять структуру объектов напрямую".
    
    Таким образом, необходимо предъявить другую модель памяти/времени, соответствующую принципам универсальности и независимости.
    
    Т.е., Машина Тьюринга вас не удовлетворила по критерию "память".
    
    У меня три вопроса:
    
    есть ли в Абстрактной Машине Тьюринга промежуточные состояния между шагами?
    
    сколько времени занимает выполнение одного шага в Абстрактной Машине Тьюринга?
    
    что такое "непрерывный алгоритм"?
    
    Ramayasket Автор
    30.07.2023 21:32
    #25806714
    1) Промежуточных состояний нет ни в машине Тьюринга, ни в ФОРАОН. Потому что любое промежуточное состояние будет просто ещё одним шагом.
    
    2) Выполнение одного шага не может "занимать" сколько-то времени, потому что "занимать" -- это ссылка на физическое время. Если угодно, шаг в абстрактной машине "занимает" 1. Просто 1.
    
    3) Пример непрерывного алгоритма: для каждой точки отрезка записать точку на 10 ниже. Получится копия отрезка. Но дискретно точки перебрать нельзя, поэтому такую операцию можно выполнить только в воображении.
    
    flancer
    30.07.2023 21:32
    #25806886
    +1
    Вот и я о том же. Время, в том числе и физическое, это самый высокочастотный процесс в какой-то среде (например, Вселенной или Машине Тьюринга), не имеющий промежуточных состояний. Переход между шагами этого процесса происходит мгновенно с точки зрения наблюдателя, являющегося частью этой среды. Вот это "1" и является базовой частотой (смены состояния среды). Я уверен, что и в нашей Вселенной есть некий процесс, события в котором происходят с наибольшей возможной для нашей Вселенной частотой (тактовой). Быстрее наша Вселенная меняться не может. Вот это изменение состояния в базовом процессе и есть "время". В унисон с ним атом цезия-133 меняет своё состояние, а мы уже считаем свою секунду. Бесконечно малого в физическом мире не существует. В конце-концов мы упираемся в "пиксель".
    
    Отсюда следует и заблуждение относительно непрерывного алгоритма. Мы не переносим каждую точку непрерывного отрезка на 10 ниже. Мы переносим начало, конец и всё, что между ними. Вполне себе алгоритмизируемая операция, в том числе и в воображении. Если вы вдруг решите переносить отрезок поточечно, пусть даже и в воображении, вы умрёте раньше, чем завершите. Либо в конце-концов придёте к осознанию дискретности материи (или хотя бы пространства, если вы не сторонник "эфира" :) ). Зенон так и сделал в своих апориях.
    
    Спасибо за статью и комментарии. Это было увлекательно!
    
    Ramayasket Автор
    30.07.2023 21:32
    #25806958
    +1
    Действительно, физическая вселенная дискретна. Но математика-то не ограничивается дискретными объектами. В том-то и её удобство, это идеализация.
    
    flancer
    30.07.2023 21:32
    #25806472
    Это я сгоряча написал. Не подумав как следует. Потом коммент подправил :)

MasterMentor
30.07.2023 21:32
#25805526
Что ЭТО??!
1. Ramayasket Автор
  30.07.2023 21:32
  #25805532
  +1
  Спасибо за внимание, но может лучше вопросы по существу?

olegchir
30.07.2023 21:32
#25805578
+5
Это очень, очень хорошая статья.

Не могу прокомментировать, пока не прочитал внимательно, но шлю лучи поддержки и свои +3

Но в комментах у тебя будут минусы. Людей не отпугнёт плашка "сложно" по отношению к статье, написанной для специалистов в математической логике, они будут писать "мышление нельзя описать непонятными буковками!111 адын адын"
1. 0xd34df00d
  30.07.2023 21:32
  #25806202
  Я пытаюсь косить под человека, приближающегося к началам становления специалистом по математической логике, и иногда даже успешно. Так вот, ИМХО статья — Корчеватель.
  1. Ramayasket Автор
    30.07.2023 21:32
    #25806236
    +1
    Очень удобно оценивать одним словом, не надо приводить доводы по существу.
  1. flancer
    30.07.2023 21:32
    #25806618
    +1
    И почему у вас сложилось такое впечатление? Если данная публикация - это "псевдонаука", то тогда настоящей "науке" будет легко это показать, разве нет? Я лично, по крайней мере, не нашёл в публикации ничего похожего на "параметр латентности, выраженный в Цельсиях". Но я даже и не пытаюсь "косить под человека, приближающегося к началам". Буду признателен, если вы мне укажите на такой момент (или такие моменты) в статье, из которого будет понятно, что автор вводит читателей в заблуждение.
    
    0xd34df00d
    30.07.2023 21:32
    #25807818
    -2
    Если данная публикация — это "псевдонаука", то тогда настоящей "науке" будет легко это показать, разве нет?
    
    Так как размежевание дискурса приводит к реинтеграции знаний, это вместе со второй теоремой Гёделя о неполноте показывает, что гносеологическая картина восприятия мира неполна.
    
    Опровергайте.
    
    Ramayasket Автор
    30.07.2023 21:32
    #25807862
    Теоремы Гёделя ничего не говорят о гносеологической картине мира, лишь о имеющейся формальной арифметике. В этих теоремах семантика заменена на синтаксис, а истинность — на выводимость (Википедия).
    
    0xd34df00d
    30.07.2023 21:32
    #25807878
    -1
    (Википедия)
    
    Про «ничего не говорят о» там нет.
    
    Ramayasket Автор
    30.07.2023 21:32
    #25807888
    Кроме того, из этих теорем не следует, что человеческие способности к познанию так или иначе ограниченны. Нет, теоремы всего лишь показывают слабости и недостатки формальных систем[23].
    
    0xd34df00d
    30.07.2023 21:32
    #25807904
    -1
    И снова мимо, я лишь говорил о гносеологической картине мира.
    
    flancer
    30.07.2023 21:32
    #25808098
    Т.е., выходит, что "Корчеватель" к данному посту плохо применим. В "Корчевателе" псевдонаучность показывалась элементарно: "параметр латентности, выраженный в Цельсиях".
    
    У вас действительно хорошо получается "косить под человека, приближающегося к началам становления", но плохо получается подкреплять свою точку зрения аргументами.
    
    0xd34df00d
    30.07.2023 21:32
    #25808168
    Т.е., выходит, что "Корчеватель" к данному посту плохо применим.
    
    Не выходит.
    
    параметр латентности, выраженный в Цельсиях
    
    В чём псевдонаучность? Если у параметра латентности есть распределение вероятностей, соответствующее по сути своей максвелловскому, то с соответствующим выбором констант на доске её вполне можно выражать в Цельсиях.
    
    И обратно, вот что вообще значит этот произвольно взятый из статьи пассаж?
    
    Модель пустого движения найдём "методом горшочка". Рассмотрим директор. Он представляет собой контракт, над базисом которого надписан один из полюсов. Представим, что контракт — это горшочек, внутри которого лежит надписанный полюс (контракт выполняет функцию памяти в отношении надписанного полюса). Тогда пустой горшочек — это контракт, над которым полюс не надписан. Отсюда алгоритм пустого движения есть контракт.
    
    Так надписан полюс над директором-контрактом или не надписан? Тут даже в одном абзаце взаимоисключающие параграфы. Откуда отсюда алгоритм пустого движения — контракт?
    
    Доказательства аксиом теории множеств там тоже очень классные. Мне б так на экзаменах разрешали доказывать, моя жизнь была бы сильно проще.
    
    В статье есть куча умно звучащих слов, призванных как будто запутать читателя. Ничего другого в статье нет. Смысла в ней тоже нет, при этом требовать от читателей показывать отсутствие смысла и по дефолту считать, что он там есть — это издевательство над здравым, ээ, смыслом.
    
    Ramayasket Автор
    30.07.2023 21:32
    #25808260
    Так надписан полюс над директором-контрактом или не надписан?
    
    Над базисом контракта директора полюс надписан.
    
    Над пустым контрактом -- не надписан.
    
    0xd34df00d
    30.07.2023 21:32
    #25808270
    +1
    Ну, исправляйте определения, чтобы они это допускали, и чтобы текст не был внутренне противоречив.
    
    flancer
    30.07.2023 21:32
    #25808806
    С аргументацией уже получше.
    
    Я, например, тоже не люблю издевательства над здравым смыслом, поэтому не стал по дефлоту считать, что в вашем комментарии есть смысл, и попросил показать его наличие. Моя изначальная просьба, если вы её перечитаете ещё раз, как раз и сводилась к тому, чтобы вы аргументировали свою точку зрения, а не просто её продекларировали.
    
    0xd34df00d
    30.07.2023 21:32
    #25808840
    Я, например, тоже не люблю издевательства над здравым смыслом, поэтому не стал по дефлоту считать, что в вашем комментарии есть смысл, и попросил показать его наличие.
    
    Хороший подход. Только почему вы его не применили к исходной статье?
    
    flancer
    30.07.2023 21:32
    #25808948
    Ну, как бы человек писал, старался. Перед этим думал ещё. Может быть даже правил, корректировал. Написал много умных слов, ввёл какие-то обозначения. Я вот в этом всём совсем плохо разбираюсь. А вы пришли и лаконично так: "Так вот, ИМХО статья — Корчеватель."
    
    Я полез посмотреть, что такое "Корчеватель" (даже ссылочку в комменте приложил). Ну, думаю, раз вы так хорошо в этом во всём разбираетесь, то для вас не составит труда мне пальцем указать на что-то совсем уж явно "псевдонаучное", что даже до меня дойдёт. Ну, как "латентость в Цельсиях". Хотя для вас, как потом оказалось, латентность в Цельсиях вполне научна, чем вы меня ещё больше запутали: "Корчеватель" - это научная статья или псевдонаучная (квазинаучная)? И как отделить одно от другого? Вот Гельфанд, например, считает, что "латентность в Цельсиях" - это "предостерегающий флажок", говорящий о бессмысленности и несуразности, а вы нашли в этом смысл. Вот я и подумал, что человек такого интеллектуального размаха, как вы, вполне может сэкономить мне немножечко времени, просто пальцем показав на псевдонаучность данной публикации. А вы вместо этого шарады с Гёгелем затеяли. Нехорошо это. Вы всё-таки на Хабре, а не в РАН. Тут совсем простые люди зачастую попадаются.
    
    0xd34df00d
    30.07.2023 21:32
    #25809032
    Ну, как бы человек писал, старался. Перед этим думал ещё. Может быть даже правил, корректировал. Написал много умных слов, ввёл какие-то обозначения.
    
    А, ну призы за участие — это модно, да.
    
    Хотя для вас, как потом оказалось, латентность в Цельсиях вполне научна, чем вы меня ещё больше запутали.
    
    Латентность в Цельсиях настолько же научна, насколько формулировки в исходной статье. И именно в этом смысл примера.
    
    Вот Гельфанд, например, считает, что "латентность в Цельсиях" — это "предостерегающий флажок", говорящий о бессмысленности и несуразности
    
    Как там наш писатель-старатель писал? «Очень удобно оценивать одним словом, не надо приводить доводы по существу.» У Гельфанда есть доводы по существу, почему это предостерегающий флажок?
    
    а вы нашли в этом смысл.
    
    Я пытался показать, что при особом желании смысл можно найти вообще в любом утверждении, записанном человеческим языком.
    
    сэкономить мне немножечко времени, просто пальцем показав на псевдонаучность данной публикации
    
    Это вообще не всегда возможно, вот так взять и пальцем показать, потому что требуется доказывать отсутствие связи между разными утверждениями, а это тяжело.
    
    Попробуйте показать пальцем псевдонаучность фразы о размежевании дискурса (которую я с утра выдумал, едва проснувшись).
    
    flancer
    30.07.2023 21:32
    #25809192
    Я уже понял, что вы при особом желании можете найти смысл в любом утверждении, а можете не найти, если желание отсутствует. Сделать вывод о том, что эта публикация является "Корчевателем" вы можете легко, но доказать этот свой вывод для вас является тяжким трудом. И я не сомневаюсь, что вы сами найдёте смысл в своей фразе о размежевании дискурса, придуманной спозаранку, а если захотите, то даже несколько смыслов. А если постараетесь, то даже несколько противоречащих друг другу смыслов. Весь вопрос: зачем? У вас 47К комментов в профиле. Вам действительно настолько скучно?
    
    0xd34df00d
    30.07.2023 21:32
    #25809204
    Ура, вместо обсуждения смысла статьи вы дошли до соломенных чучел и до обсуждения личностей. Это, конечно, лучшее математическое доказательство всех смыслов, прямо в духе исходной статьи с «патамушта Декарт».
    
    0xd34df00d
    30.07.2023 21:32
    #25812384
    А, значит, делать отсылки к личности тут принято. Ну ок, исправимся.
    
    Мне бы всё-таки хотелось услышать от восходящей звезды латвийской веб-разработки, которая неспособна понять смысл аналогий, но несомненно обладает сверхразвитым интеллектом и навыками, чтобы рассуждать о статьях по формальной логике, почему безосновательные слова Гельфанда о флажочках не требуют никаких обоснований, и вас устраивают.
1. smrl
  30.07.2023 21:32
  #25813972
  А вы точно настоящий "специалист в математической логике"?

avshkol
30.07.2023 21:32
#25805580
+1
Дочитал до $\{m,t,x\}$ - здесь, думаю, хорошо бы разъяснить, что такое m - память? Мне вот совершенно не понятно...
1. Ramayasket Автор
  30.07.2023 21:32
  #25805588
  -1
  Память -- это любое устройство или система, которая может хранить в себе разные объекты. Примеры: RAM, память человека, лента машины Тьюринга, или доска. Примеров и в природе, и искусственных -- очень много. Если вам нужно что-то хранить -- вам нужна память.
1. olegchir
  30.07.2023 21:32
  #25805590
  Они доопределяются ниже, там целый раздел "Математическая реальность" про неформальную суть памяти

olegchir
30.07.2023 21:32
#25805618
+4
Заметка: кажется, что эта статья описывает логику рассуждений, используемую при вдумчивом мышлении на манер работы с математикой или ведения разговора в стиле аристотелевской логики.

В реальности, кажется, люди не столько думают, сколько подбирают ближайшие похожие цепочки в простанстве гиперпараметров, в ходе процесса, чем-то отделенно напоминающего LLM. Он руководствуется не логикой, а похожестью. По типу того, что если спросить у человека подряд несколько вопросов формата "снег на улице какого цвета?", "молоко какого цвета?", "корова издаёт какой звук?" и добить вопросом: "а что пьёт корова?", человек с высокой вероятностью ответит: "молоко". Этот ответ руководствуется скорее поиском внешнего лингвистического подобия, чем построением внутреннего понимания функционирования коровы.

То есть, описанная модель хоть и имеет место быть, но относится с супер редкой модели мышления на основе выводов, которая в реальной жизни встречается черезвычайно, исключительно редко (например, в ходе работы математика или юриста)
1. Ramayasket Автор
  30.07.2023 21:32
  #25805636
  +1
  Ваш комментарий относится к той части работы, которая ещё не опубликована -- специальный раздел низшей математики. В этой (общей) части речь в основном про математические объекты -- мышление здесь присутствует только в виде математической реальности.

Ramayasket Автор
30.07.2023 21:32
#25805626
комментарий перенесён ↑

smrl
30.07.2023 21:32
#25805894
+3
Универсальный, структурированный язык обеспечивает надлежащую формализацию любых знаний, с явной передачей смысла без потерь.

Любых знаний - это очень круто! А можно какой-нибудь практический пример? Как будет выглядеть на этом вашем языке формализация, ну допустим, того, чем табуретка отличается от стола?
1. Ramayasket Автор
  30.07.2023 21:32
  #25806038
  Табуретка и стол описываются более сложными понятиями, нежели ФОРАОН. Но когда вы будете далее разбивать их на более простые понятия, вы до этого языка и дойдёте. "Любых знаний" означает, что вы в любом случае дойдёте до приведённых в статье абстракций.
  
  Здесь нет чудес. Чтобы ответить на ваш вопрос, ФОРАОН не требуется, он не может потребоваться там, где достаточно обычных понятий.
  1. Abobcum
    30.07.2023 21:32
    #25807088
    +1
    Возможно, у автора найдётся хотя бы один практический пример. Ну, как в школе объясняют математику,знаете?, яблоки и землекопы, числа для счёта предметов... Ведь именно на этих уроках дети с абсолютно чистым разумом начинают с этих самых "простых понятий". Tabula rasa. Кажется, именно сюда и напрашивается ваша гипотеза.
    
    Ramayasket Автор
    30.07.2023 21:32
    #25807110
    Столы и табуретки -- понятно как устроены, вопросов ни у кого (почти) не вызывают. А вот устройство основных математических объектов ранее не описывалось. Только аксиомами. А здесь предъявляется структура чисел и множеств (в том числе), а аксиомы доказываются.
    
    Это разве не практический пример?
    
    Уровень статьи - "сложный". Я не возьмусь это объяснять детям.
    
    Abobcum
    30.07.2023 21:32
    #25807152
    +2
    Т.е. вы просто заменили старую аксиоматику на новую, подобранную таким образом, что она доказывает старую? И никаких других целей и практической пользы не закладывали в свои труды?
    
    Ramayasket Автор
    30.07.2023 21:32
    #25807172
    Нет, я не заменял старые аксиомы на новые. В моей работе не вводятся никакие аксиомы -- при описанной структуре объекта аксиомы не нужны. Доказательство аксиом никогда не рассматривалось как возможное, но оно стало таковым, в этом и цель, и практическая польза для математики.
    
    Вы заметите отсутствие новых аксиом, если дочитаете до конца.
    
    Другая польза в том, что на основе этой работы ИИ сможет понимать математику.
    
    Abobcum
    30.07.2023 21:32
    #25807228
    +1
    Уточним, что НП не является аксиомой: его нет нужды принимать на веру, т.к. способность формулировать осмысленные высказывания уже доказывает и разумность, и существование их автора.
    
    Так вот же ваша аксиома о НП, а конкретнее:
    
    способность формулировать осмысленные высказывания уже доказывает и разумность, и существование их автора.
    
    Вот у вас что-то одно уже автоматически и самоочевидно доказывает что-то другое - классическая аксиома.
    
    Ramayasket Автор
    30.07.2023 21:32
    #25807240
    Аксиома это утверждение, принятое на веру. Вы же не принимаете на веру способность человека думать? Это доказанный факт. Почитайте про cogito, ergo sum, оно очень подробно разобрано. Никто и никогда не считал его аксиомой.
    
    Оно доказывает не что-то другое, а само себя.
    
    Abobcum
    30.07.2023 21:32
    #25807858
    +3
    Разумеется нет, но у вас из воздуха появляются такие сущности как
    
    автор
    
    осмысленное высказывание
    
    Способность формулировать
    
    Разумность
    
    Существование
    
    При этом и эти базисы, и само доказательство отсутствует.
    
    Иными словами, большинство рассуждений (не могу назвать их математическими выкладками) базируются на 5 фактах, которые, строго говоря, необходимо ещё и доказать. Вот тогда можно будет проверить дальнейшие выводы и претендовать на научность.
    
    0xd34df00d
    30.07.2023 21:32
    #25807884
    Это доказанный факт.
    
    Покажите математическое доказательство плиз.
    
    Ramayasket Автор
    30.07.2023 21:32
    #25807900
    Математика сама по себе является доказательством разумности человека разумного, который её придумал/обнаружил.
    
    0xd34df00d
    30.07.2023 21:32
    #25807908
    Это не математическое доказательство.
    
    Ramayasket Автор
    30.07.2023 21:32
    #25807914
    И как это мешает делу?
    
    0xd34df00d
    30.07.2023 21:32
    #25808174
    Если вы строите математическую теорию, то неплохо бы опираться при её построении на математические доказательства.
    
    Ramayasket Автор
    30.07.2023 21:32
    #25808184
    Нельзя проверить математику математикой же. Нужен внешний источник, такой как Декарт.
    
    0xd34df00d
    30.07.2023 21:32
    #25808192
    Нельзя проверить математику математикой же.
    
    Кто запретил? Разделение на language и metalanguage прошло мимо вас?
    
    Нужен внешний источник, такой как Декарт.
    
    А чем я хуже Декарта? Я вот проверяю вашу статью и говорю, что это ерунда. Принимаем как доказанный факт и первичную достоверность?
    
    Ramayasket Автор
    30.07.2023 21:32
    #25808208
    +1
    А чем я хуже Декарта?
    
    ...
    
    0xd34df00d
    30.07.2023 21:32
    #25808240
    У вас текст комментария куда-то делся.
    
    Ramayasket Автор
    30.07.2023 21:32
    #25807982
    Это утверждение Декарт выдвинул как первичную достоверность, истину, в которой невозможно усомниться — и с которой, следовательно, можно начинать отстраивать здание достоверного знания. (Википедия)
    
    0xd34df00d
    30.07.2023 21:32
    #25808186
    Это — математическое доказательство? «Декарт выдвинул»?
    
    Ramayasket Автор
    30.07.2023 21:32
    #25808194
    Это НЕ математическое доказательство
  1. smrl
    30.07.2023 21:32
    #25807254
    +2
    Намеки не доходят. Ясно...
    Ну если хотите в лоб, то вот вам по лбу: ваша стартовая посылка, что раз математические фразы часто пишут на плоскости, то значит математика по сути своей и является преобразованием символов на плоскости, - это такой же неотрефлексированный бред, как утверждение великого ученого товарища Сталина, что человек размышляет словами, поскольку именно словами он потом передает свои мысли другим людям.
    
    Мне, на самом деле, другое интересно. Я почему за статью зацепился-то. Вот это вот:
    
    Хотя математика и управляет материальным миром (и вроде бы существует "сама по себе"), думать о математике может только человек -- субъект, обладающий разумным мышлением.
    
    - это вы сами дошли, или по мотивам Пенроуза, или еще кого-то?
    
    Ramayasket Автор
    30.07.2023 21:32
    #25807270
    ...то значит математика по сути своей и является преобразованием символов на плоскости, - это такой же неотрефлексированный бред...
    
    Этого в моей статье нет -- это ваша додумка. Согласен с её характеристикой.
    
    В статье написано, что математика имеет дело со структурой и информацией. Символы на плоскости выражают и то и другое, но не заменяют их.
    
    это вы сами дошли
    
    Если в вашем окружении есть не-человек, который умеет думать -- скорее публикуйтесь.
    
    smrl
    30.07.2023 21:32
    #25807750
    Попыткам сделать алгоритмический ИИ - сто лет в обед. Но последние пятьдесят лет люди уже поняли, что правила преобразования симоволов, задаваемые ручками заранее и навсегда (что вы и пытаетесь делать всю статью) - к ИИ не приводят, даже если сделаны на совесть (а не как у вас, помесь французской логики с нижегородскими "досками", "ластиками", "движениями" и "временем").
    Впрочем, дело ваше. Хотите сходить с ума, сходите.
    
    Ramayasket Автор
    30.07.2023 21:32
    #25807770
    1) Данная статья не имеет отношения к попыткам сделать ИИ, она чисто математическая.
    
    2) В статье вообще нет никаких преобразований символов.
    
    Итого, ваши доводы полностью укладываются в написанное здесь.
    
    smrl
    30.07.2023 21:32
    #25813930
    Тяжела судьба непризнанного гения.
    В рецензируемый журнал обратиться не пробовали?

anonymous
30.07.2023 21:32
#25806502
НЛО прилетело и опубликовало эту надпись здесь
1. Ramayasket Автор
  30.07.2023 21:32
  #25806528
  ага, никто никогда ранее не исследовал, пришел автор и открыл мир
  
  Модель мышления ранее в математику не вводилась. И структура чисел, множеств и т.д. ранее не предъявлялась.
  
  Похоже, что для написания комментария вы дочитали только введение.

michael_v89
30.07.2023 21:32
#25807452
+4
Чтобы подобное стало возможным для АММ, она должна обладать встроенным способом хранения знаний, который представляет структуру объектов напрямую, т.е. выражает их композицию, а не кодирует их при помощи третьих объектов.

Не объяснено, что означает "напрямую", то есть как определить, что некоторая система хранит их именно напрямую, а не с помощью третьих объектов.
С моей точки зрения хранение в некоторой системе информации о состоянии стороннего объекта без системы кодирования принципиально невозможно. Так как информация от объекта до системы обычно передается не в том виде, в котором хранится.

Тройку {m,t,x} будем называть смешанной системой (англ. mixed system)

Раз есть смешанные системы, значит есть и несмешанные. Что такое "несмешанная система"? Почему вы их не рассматриваете?

Действительно, кварки хранят цвет, а глюоны его меняют; таким образом, кварки играют роль памяти, глюоны роль времени, а цвет есть хранящийся в памяти объект.

Нет, раз глюон меняет цвет кварка на другой, значит у него есть свое состояние "цвет" или "дельта цвета", которое в нем хранится.
И кварк и глюон являются системами, в которых есть элементы "память, время, объекты в памяти", то есть смешанными системами. Любой физический объект имеет состояние.
Вы назначаете схожим вещам разные роли по своему усмотрению. Это не выглядит логично.

Что касается нейронной сети, то данная структура моделирует не разум, а мозг

Утверждение без доказательств. А я утверждаю, что она моделирует разум. Считаем, что я опроверг вашу теорию? Или все-таки для таких утверждений нужны доказательства?

Причем не показано, почему это имеет значение, так как по общепринятому представлению разум это результат деятельности мозга, а значит моделирование мозга означает и моделирование разума.

переход от взаимодействия нейронов и импульсов к мышлению есть переход от количества к качеству

Утверждение без доказательств. А я утверждаю, что не есть.

который не учитывается нейронной сетью как моделью

Утверждение без доказательств. А я утверждаю, что учитывается.

т.к. лента не даёт возможность представлять структуру объектов напрямую; символы всего лишь кодируют её при помощи некоторого языка.
Содержимое ленты нуждается в интерпретации в рамках этого языка, что не соответствует принципу независимости.

Вообще-то лента в машине Тьюринга это и есть абстрактная память, которую вы рассматриваете.
Содержимое памяти, о которой говорите вы, тоже должно быть записано на некотором языке и нуждается в интерпретации.
Без системы интерпретации невозможно извлечь информацию.

Пример. Абстрактная мыслящая система с элементами "память, время, объекты в памяти" смотрит на Луну. Луна имеет желтоватый цвет. Как информация о цвете хранится в памяти системы?

Определения даются при помощи оригинальной графической нотации и программного кода на языке C#
Формальной семантикой будем называть способ представления смысла, явно (напрямую) выражающий структуру. Данная работа обнаруживает, что математическая реальность достаточно богата для этого.
Мы используем язык программирования, чтобы выразить структуру излагаемой идеи

То есть никакого способа представления структуры объектов "напрямую" у вас нет, вы используете кодирование при помощи некоторого языка — русского, C#, математической нотации. И если подумать, то будет ясно, что такая же задача объяснения возникает при передаче информации между любыми элементами системы.

Далее лень разбирать. Вывод — статья основана на необоснованных или нелогичных утверждениях, которые считаются истинными, потому что автору так захотелось, не стоит воспринимать ее всерьез.
1. Ramayasket Автор
  30.07.2023 21:32
  #25807576
  Для разнообразия хотя бы анализируете написанное. Спасибо. Далее по пунктам.
  
  Не объяснено, что означает "напрямую"
  
  Например, записать натуральное число, следующее за единицей, как "два" или 2 -- это не напрямую. Т.к. эта запись не показывает, из каких элементов оно состоит и как они соединены. В то время как Рис. 11ii именно это и отражает.
  
  Что такое "несмешанная система"? Почему вы их не рассматриваете?
  
  Объекты в памяти в отрыве от последней -- пример не смешанной системы. Необходимости их рассматривать нет -- про них и так написано более чем достаточно.
  
  Нет, раз глюон меняет цвет кварка на другой, значит у него есть свое состояние "цвет" или "дельта цвета", которое в нем хранится.
  
  Всё верно, кроме слова "нет". Маркер имеет внутреннюю память для хранения алгоритма, также и кварк хранит внутри себя изменение цвета.
  
  А я утверждаю, что она моделирует разум
  
  Если так утверждаете, напишите, каким единственным способом представить в нейронке композицию числа , или структуру сферической поверхности. Разум способен рассуждать, нейронная сеть такой способностью не обладает.
  
  Утверждение без доказательств. А я утверждаю, что не есть.
  
  Если бы не было перехода от количества к качеству, то рассуждать могла бы и кошка. Но, не рассуждает. Это надо доказывать?
  
  Содержимое памяти, о которой говорите вы, тоже должно быть записано на некотором языке и нуждается в интерпретации
  
  Только вот язык, который используется, включает в себя единственный символ, передающий структуру -- примитив. Он соответствует пустой системе, и все более сложные объекты строятся из него. Диаграммы ФОРАОН явно выражают структуру, и классы тоже.
  
  Как информация о цвете хранится в памяти системы?
  
  А как бы вы описали цвет? Например тремя числами - RGB. Как хранить цвет, не относится к теме работы. Как описывать табуретки, тоже.
  
  То есть никакого способа представления структуры объектов "напрямую" у вас нет
  
  Это уже было отвечено выше.
  
  Далее лень разбирать
  
  Вот здесь и есть корень
  1. michael_v89
    30.07.2023 21:32
    #25808736
    +2
    Т.к. эта запись не показывает, из каких элементов оно состоит и как они соединены.
    Получившийся объект в мнемонической форме можно записать как "переместить, переместить, стоп"
    
    Почему вы решили, что число 2 состоит из перемещений на 1, а не на 0.1?
    Почему вы решили, что один из элементов числа 2 это "стоп", почему недостаточно просто "переместить, переместить"?
    Почему "стоп" после первого перемещения можно пропускать? Если он важен, то должно быть "переместить, стоп, переместить, стоп".
    
    Я вот могу описать число 2 как "начать из точки 0, переместить, переместить". Финальный "стоп" у меня подразумевается автоматически из конечности перемещения на один шаг. Почему мы должны считать ваше описание более правильным, чем мое?
    
    Вы утверждаете, что любой человек, который работает с числом 1000000, хранит в памяти миллион перемещений от 0? Если нет, значит для существования разума такое хранение "напрямую" не требуется.
    
    Ваша теория порождает много вопросов, и я сомневаюсь, что у вас есть на них ответы.
    
    В то время как Рис. 11ii именно это и отражает.
    
    Нет, рисунок 11ii показывает не "напрямую", а с кодированием на придуманном вами графическом языке. И не число 2, а как от точки 0 попасть в точку 2 движениями по 1.
    
    — Всё верно, кроме слова "нет".
    
    Если остальное верно, то и слово "нет" верно. Слово "нет" означает, что ваше утверждение неверно. Кварки не играют роль памяти, кварки это тоже смешанная система со всеми тремя элементами, как и глюоны.
    
    Маркер имеет внутреннюю память для хранения алгоритма, также и кварк хранит внутри себя изменение цвета.
    
    Я не вижу, как это опровергает мое утверждение. И кварк, и глюон хранят внутри себя информацию о цвете, поэтому оба являются полноценными смешанными системами.
    
    Если так утверждаете, напишите, каким единственным способом представить в нейронке композицию числа i
    
    Вы никакого доказательства не написали, почему я должен что-то писать? Вы сделали утверждение без доказательств и рассуждаете так, как будто оно верное. Значит я могу сделать так же. Раз по этим критериям мое утверждение верное, значит я опроверг вашу теорию.
    Либо оба наши утверждения верными считать нельзя, и раз вы сделали утверждение первым, то с доказательств должны начать вы.
    
    каким единственным способом представить в нейронке композицию числа i
    
    Вы не доказали, что единственность способа является определяющим критерием разума.
    Более того, любой сложный объект состоит из нескольких более простых частей, и их можно описывать в разном порядке, что дает комбинаторное количество вариантов описания. Например, составная гантеля состоит из ручки и 2 одинаковых блинов. Какая из этих 3 частей в единственном способе описания этого объекта идет первой?
    
    Разум способен рассуждать, нейронная сеть такой способностью не обладает.
    
    Современные нейросети такой способностью не обладают. Из этого не следует, что никакие нейросети, которые могут появиться через некоторое время, не смогут рассуждать.
    
    Если бы не было перехода от количества к качеству, то рассуждать могла бы и кошка. Но, не рассуждает. Это надо доказывать?
    
    Если вы считаете это доказательством утверждения про переход, то да, его надо было написать вместе с этим утверждением.
    Про кошку я ничего доказывать не просил. Но если вы делаете утверждение, что она не рассуждает, то да, его надо доказывать. Потому что с моей точки зрения кошка вполне себе рассуждает.
    
    Только вот язык, который используется, включает в себя единственный символ, передающий структуру — примитив. Он соответствует пустой системе, и все более сложные объекты строятся из него.
    
    Во-первых, кроме самого примитива у вас есть еще и то, что вы обозначаете черточкой между ними. Уже поэтому ваше утверждение ложно.
    Кроме того, у вас есть третий символ "краска", который к тому же бывает разных видов. Это язык кодирования.
    
    Как хранить цвет, не относится к теме работы.
    
    Относится, потому что вы утверждаете, что для него не должно использоваться кодирование при помощи некоторого языка.
    
    Как описывать табуретки, тоже.
    
    Относится, так как вы говорите про способ представления знаний в абстрактной модели мышления (т.е. разума). Значит ваша теория должна показывать, как разум описывает знания о конкретной табуретке.
    
    Вот здесь и есть корень
    
    Нет. Любые выводы, основанные на неверных посылках, некорректны, и могут дать ложный результат, поэтому рассматривать их нет смысла. Даже если логика, примененная к этим посылкам, верна.
    
    Ramayasket Автор
    30.07.2023 21:32
    #25809980
    +1
    Ваша теория порождает много вопросов, и я сомневаюсь, что у вас есть на них ответы
    
    Ответы есть, надо над ними поработать. Ваш последний комментарий по делу; во всяком случае, ваши возражения стали понятны. Надо подумать, как написать интегрированный ответ и/или внести правки в статью, потому что формат комментария "цитата-реплика" не сильно удобен при больших размерах.
    
    Ramayasket Автор
    30.07.2023 21:32
    #25810336
    Ответил на часть возражений в корне комментариев
    https://habr.com/ru/articles/751058/comments/#comment_25810332
    
    Вторую часть напишу позже, чтобы не валить в одну кучу. Прокомментируйте пока первую часть, пожалуйста.
  1. michael_v89
    30.07.2023 21:32
    #25809692
    +1
    Чтобы подобное стало возможным для АММ, она должна обладать встроенным способом хранения знаний, который представляет структуру объектов напрямую, т.е. выражает их композицию, а не кодирует их при помощи третьих объектов.
    
    А, наконец-то понял. Это выражение следует читать так:
    "способом хранения знаний, который представляет структуру объектов в виде композиции элементарных обозначений, а не кодирует их при помощи введения новых обозначений для каждого нового объекта".
    
    Отсюда непонятно, почему 3 элементарных обозначения вида "перемещение" и "стоп" обязательно означают разум, а большее число элементарных обозначений нет (например отдельные 10 цифр).
    Или почему разум не может назначить какой-то сложной композиции элементарных обозначений короткое неэлементарное обозначение и работать с ним. Любые термины это и есть такие обозначения, то есть третьи объекты.

Ramayasket Автор
30.07.2023 21:32
#25807758
+1
Итак, прошло 15 часов с момента публикации. Надо отдать должное @olegchir: он точно знал, что будет. Весь день отвечаю на комментарии, и уже можно указать на ряд общих моментов.

Популярный modus operandi:
- Прочитать несколько начальных разделов
- Прочитанное дополнить своими додумками
- Остальное проигнорировать (цитата - "лень")
- Полученную проекцию статьи объявить "бредом" (цитата) -- самое смешное, вполне заслуженно, ибо к содержанию статьи такая проекция не имеет никакого отношения
В этой связи надо уточнить вот что.

Все выводы в статье ПРОВЕРЯЕМЫ. Для всех объектов указана цепочка обоснования, структура и информация. Если вы видите необходимость дискуссии, ПОЖАЛУЙСТА, прочитайте статью до конца. Оцените выводы. При написании возражений, указывайте конкретную цепочку рассуждений и то место в ней, с которым вы не согласны.

ИМХО, такой способ беседы будет куда продуктивнее. Спасибо.

P.S. Примите во внимание, что статья не относится к написанию ИИ, не рассматривает работу мозга или работу физических компьютеров.
1. 0xd34df00d
  30.07.2023 21:32
  #25809878
  Операнди так операнди.
  Пойду ткну в рандомное место и найду там в ε-окрестности ошибку. Ну, не совсем в рандомное: я в основном смотрел в районе описания связи с теорией множеств, потому что её я понимаю.
  
  Так вот, давайте возьмём конкретное определение 8.5. Вас не смущает, что вы понятие равенства (с [мета?]переменными A и B) определяете через себя же? Ну, вон справа от трёх горизонтальных палочек стоит C = A, D = B. Чем = справа отличается от = слева?
  1. Ramayasket Автор
    30.07.2023 21:32
    #25809954
    Ну, вон справа от трёх горизонтальных палочек стоит C = A, D = B
    
    Это присваивание. Внутри алгоритма же.
    
    0xd34df00d
    30.07.2023 21:32
    #25810222
    Что такое присваивание?
    
    Ramayasket Автор
    30.07.2023 21:32
    #25811358
    Присваивание C = A это запись значения A в переменную C. Чтение A и запись в C при помощи маркера.
    
    0xd34df00d
    30.07.2023 21:32
    #25812368
    Так вы не формализовали понятие маркера, а только дали некоторую интуицию, что это такое.
    
    Ramayasket Автор
    30.07.2023 21:32
    #25812510
    Формализация маркера - код на C#
    
    0xd34df00d
    30.07.2023 21:32
    #25812514
    То есть, для вашей теории нужно тащить всю семантику C# (в которой, конечно, понятия множеств, присваиваний и равенств никак не используются). Хорошая теория!
    
    Ramayasket Автор
    30.07.2023 21:32
    #25812544
    В статье написано, что язык C# используется для того, чтобы формализовать действие, и выразить структуру. Он просто показывает, из чего состоит маркер. Вы ещё скажите, что для теории надо включать в неё чернила, которыми напечатана статья.
    
    0xd34df00d
    30.07.2023 21:32
    #25812556
    Если вы говорите, что присваивание — «это как в сишарпе», то надо описывать, как это в сишарпе. Причём тут чернила, непонятно.
1. vlnel
  30.07.2023 21:32
  #25814010
  Складывается впечатление, что вы, уважаемый автор, помимо того, что вводите большое количество новых понятий, зачастую используете известные всем термины в совершенно ином значении, понятном только вам. Само по себе это не плохо, скорее, даже типично для такого рода работ с философским уклоном. Но вот чтобы понять всё это, потребуется немало усилий: возможно, придется перечитать статью несколько раз, пытаясь определить из контекста, где использованные термины имеют общепринятое значение, а где - новое, и какое именно новое значение вы подразумевали, связывая их между собой именно таким способом. Если это удастся, можно будет сделать вывод о внутренней непротиворечивости (или противоречивости) используемой системы понятий, а затем оценить возможность приложения теории к реальности. Предположу, что мало кто из читателей готов на такие затраты времени и сил ради сомнительной теории, во всяком случае, я не готов.
  
  Было бы неплохо, если бы вы привели какие-нибудь доступные примеры преимуществ, которые дает ваша теория, помимо "структура основных математических объектов, имеющая общее дерево наследования". Обладает ли она предсказательной силой? Может быть, сокращает изложение какой-нибудь математической мысли или теории (условно: было 10 страниц, стало 2)? Или закладывает основы для прорыва в области ИИ? Если да, то каким образом?
  1. Ramayasket Автор
    30.07.2023 21:32
    #25814028
    -1
    Данная работа позволила доказать аксиомы, в частности, арифметики и множеств. Что касается ИИ, то предъявленная структура математических объектов позволяет написать ИИ, который будет понимать математику на самом деле.
    
    Обо всём этом явно написано в статье.
1. smrl
  30.07.2023 21:32
  #25814038
  >> P.S. Примите во внимание, что статья не относится к написанию ИИ, не рассматривает работу мозга или работу физических компьютеров.
  
  То есть, по-вашему, "абстрактная модель мышления", способная "универсально описыать любые знания" - не будет являться сильным искуссвтенным интеллектом по определению?
  
  И потом эти люди обижаются, когда все косяки в их текстах не разбирают уважительно на ста листах.
  1. Ramayasket Автор
    30.07.2023 21:32
    #25814152
    Статья касается отдельных аспектов ИИ, в плане компонентов мыслящей системы (память и время). Но также написано, что более подробно вопросы ИИ рассматриваются в другой части работы. Возможность описывать любые знания тоже в эту копилку.
    
    Но цель данной статьи, в первую очередь -- математика, доказательство аксиом.

Wizard_of_light
30.07.2023 21:32
#25808278
В отношении ИИ, можно указать, что эта область знаний не имеет общепризнанного, твёрдого и законченного теоретического фундамента, имея в виду строгую математическую модель мышления: компоненты и структура мыслящей системы, её цели и алгоритмы их достижения.

Как насчёт "Грегорийских тварей" Деннета? ИМХО, их математическое описание вполне возможно.

математика полагает средства письма самоочевидными

Вообще-то нет, математика полагает, что некоторые объекты соотносятся по определённым правилам. Письмом это будет выражено, графикой, звуком, танцем, архитектурой, кулинарией, набором электрических зарядов в камне - совершенно без разницы.

Поскольку разум человека является смешанной системой, АММ должна включать в себя представление памяти и времени.

Для меня звучит как "в огороде бузина, потому что в Киеве дядька". АММ должна включать в себя представление о памяти и времени, потому что мы АММ описываем как смешанную систему, разум человека тут не при чём.

Среди теоретических или искусственных систем, самые очевидными примерами являются машина Тьюринга и компьютер. В машине Тьюринга роли памяти, времени и объектов играют лента, головка и символы, соответственно.

Машину Тьюринга также следует исключить, т.к. лента не даёт возможность представлять структуру объектов напрямую; символы всего лишь кодируют её при помощи некоторого языка.

Так я не понял - машина Тьюринга пример или исключение? Неявно постулируется наличие структуры у объектов. Неявно вводятся новые единицы - символы, которые противопоставляются объектам.

Отправной точкой наших рассуждений является известное из философии высказывание "я мыслю, следовательно, существую" (начальный постулат, НП). Уточним, что НП не является аксиомой: его нет нужды принимать на веру, т.к. способность формулировать осмысленные высказывания уже доказывает и разумность, и существование их автора.

Определяя основную аксиому мышления через само мышление мы тут же придём к порочному кругу. Задача доказательства существования АММ вообще не стоит - она не существует, мы её пытаемся создать. Доказательство необходимости самосознания для мышления - это отдельный квест.

В общем, извините, я тоже не осилил. ИМХО, если у нас в самом начале нет твёрдой аксиоматики и определений, то и дальше никакой математики не выйдет.
1. Ramayasket Автор
  30.07.2023 21:32
  #25808310
  Вообще-то нет
  
  Именно так. Математика не начинается с обоснования того, что на доске/листе бумаги можно писать.
  
  АММ должна включать в себя представление о памяти и времени
  
  Потому что разум является смешанной системой. А не потому что математическая реальность состоит из доски и маркера.
  
  Так я не понял - машина Тьюринга пример или исключение?
  
  Машина Тьюринга -- пример смешанной системы, но не пригодна как модель памяти/времени АММ.
  
  Определяя основную аксиому мышления через само мышление
  
  Как такой текст мог появиться в ответ на: "Уточним, что НП не является аксиомой"?!
  
  Задача доказательства существования АММ вообще не стоит - она не существует, мы её пытаемся создать
  
  АММ не изобретена, а обнаружена. Об этом говорится более чем в одном месте.
  
  если у нас в самом начале нет твёрдой аксиоматики и определений
  
  Определений более чем достаточно. Новых аксиом нет. И хорошо.

kpmy
30.07.2023 21:32
#25809610
+1
Что думаете о Комплексной Логике Зиновьева?
1. Ramayasket Автор
  30.07.2023 21:32
  #25811512
  Да ничего, в общем-то. Как это связано со статьёй?

Ramayasket Автор
30.07.2023 21:32
#25810332
Это комментарий в ответ на https://habr.com/ru/articles/751058/comments/#comment_25808736

Написан в корне, чтобы не углублять чрезмерно вложенность.

Комментарий интегрированный, т.е. вместо отдельных цитат и реплик ответ будет более целостным и удобным для прочтения.

1) По поводу представления смысла "напрямую"

В статье говорится, что объект имеет структуру и информацию. Структура -- из каких элементов состоит объект, а информация -- как эти элементы расположены в памяти. Нам важно, чтобы мы могли для любых объектов это указать.

Далее. Почему не подходит машина Тьюринга? Если на ленте записан символ 1, то глубже структуру единицы на ленте представить нельзя: человек, интерпретирующий символы, должен сам знать, что "1" есть отсылка к аксиомам Пеано. То есть сам символ "1" подходит для машины Тьюринга, но не выражает структуру этого числа.

Посмотрим теперь на язык ФОРАОН. Он имеет единственный символ для выражения структуры -- это примитив, кружочек. Поскольку он кодирует (да) нуль-систему, мы можем использовать любой символ, кружочек самый простой. Более сложные объекты -- контракт и директор -- включают в себя несколько экземпляров нуль-системы -- несколько примитивов.

Теперь про информацию. Она представлена двумя символами. Ось на доске изображается коннектором, а направления -- красками. И оси, и направления -- наблюдаются на доске непосредственно, доступны глазу. Это более прямой способ, нежели слово "ориентация", поэтому и сказано "представление смысла напрямую". Смысл слова "ориентация" надо помнить, тем более оно многозначное, и относится не только к доске, а ещё много к чему. В то время как коннектор показывает ориентацию на доске прямо как она есть.

2) По поводу представления объектов через ФОРАОН или нет (числа, табуретка, цвет и т.д.)

Я сожалею, если из статьи и комментариев создалось впечатление, что всё надо представлять только через ФОРАОН. Это, конечно, не так. Хотя ФОРАОН выражает структуру, например, единицы, это вовсе не отменяет запись типа 1+2+3. Важно, чтобы для такой записи была известна структура до самого низа, и здесь ФОРАОН в помощь. То же самое для табуретки: хотя в глубине всё и доходит до ФОРАОН, сами знания об устройстве табуретки состоят из более крупных элементов. И то же самое в отношении всего богатства математических обозначений -- ни в коем разе не предполагается это заменять на запись ФОРАОН.

3) По поводу кодирования

Согласен, что формулировка в статье неудачная. То, что слова или символы кодируют смысл при помощи третьих объектов -- это нормально. Надо было указать, что плохо, когда только кодируют без возможности явного указания структуры и информаци, а вышло так, как будто само кодирование это плохо и будто бы у меня в работе кодирования нет, что конечно же неверно.

4) По поводу представления чисел.

Прежде всего, в работе говорится, что число -- это алгоритм сдвига. Это в точности соответствует традиционному представлению числа как вектора, который имеет величину и ориентацию и направление. И да, вектор показывает, как попасть из одной точки в другую.

Работа ничего не говорит против традиционной записи числа десятичными (или другими) разрядами -- более того, есть подозрение, что наш разум так и поступает. Но! Работа не анализирует работу настоящего разума -- она лишь строит модель знаний на основе математической реальности.

Теперь рассмотрим, как представить структуру числа в терминах ФОРАОН.

Прежде всего, почему в работе число 2 представлена именно элементарными сдвигами (1), а не по 0,1 ? Потому что это более простой способ. Элементарный сдвиг у нас уже есть, и его достаточно, чтобы представить натуральное число. Для сдвигов по 0,1 нам надо определить ещё дробный (редуцированный) сдвиг, а это излишнее усложнение для натурального числа.

По поводу "стоп". В статье сказано, это сделано ради консистентности записи ФОРАОН, для устранения паразитного смысла. Если не поставить в конце пустое движение, то будет выглядеть так, что над первым директором что-то надписано, а над вторым -- нет, то есть два движения как будто отличаются, что неверно. Чтобы в структуре числа элементарные движения были одинаковы, и добавлен в конец цепочки контракт (пустое движение).

Это не означает, что при совершении сдвига на 2 совершать отдельные остановки. Сдвиг на 2 "на самом деле" просто сдвиг на 2 единым движением. Но когда мы записываем структуру этого сдвига средствами ФОРАОН, "стоп" нам нужен.

5) По поводу остальных вопросов в исходном комментарии (нейронки, кварки), будет отдельная запись, разобьём на несколько частей.
1. michael_v89
  30.07.2023 21:32
  #25810582
  т.е. вместо отдельных цитат и реплик ответ будет более целостным и удобным для прочтения.
  
  Нет, ответьте пожалуйста прямо на прямые вопросы. Вопросы вызваны вашими утверждениями, и от того, что вы их повторите еще раз, ответы не появятся. Как минимум 2 вопросы вы проигнорировали. Как и несколько моих утверждений, которые не являются вопросами, но указывают на противоречия в ваших словах. Например про то, что ваше утверждение "Он имеет единственный символ для выражения структуры" ложно. Кроме кружочка у вас есть черточки между ними.
  1. Ramayasket Автор
    30.07.2023 21:32
    #25811288
    Чёрточка не представляет структуру: она показывает, как элементы контракта (базис и полюсы) расположены вдоль оси. Чёрточка (коннектор) представляет информацию, т.е. расположение элементов в памяти.
    
    Примитивы можно объединить либо контрактом, либо акцентом, но в любом случае примимтив является единственным символом, обозначающим структуру.
    
    Кстати, я полагал, что все рассуждения о кодировании и интерпретации языка помогут лучше понять проблему, но на деле, они кажется, спорные и только усложняют понимание. Я склоняюсь к тому, что их лучше вовсе исключить: на дальнейшие определения они не влияют.
    
    Думаю, что на ряд вопросов я ответил.
  1. Ramayasket Автор
    30.07.2023 21:32
    #25811380
    Как минимум 2 вопросы вы проигнорировали. Как и несколько моих утверждений
    
    Чтобы не плодить огромные простыни, предлагаю отталкиваться от этого, и итерационно по одному дополнять, где и что вам видится не отвеченным.
    
    michael_v89
    30.07.2023 21:32
    #25812448
    Чёрточка (коннектор) представляет информацию
    
    Если она представляет какую-то информацию, значит одного символа вам недостаточно, чтобы это выразить. Поэтому утверждение, что у вас единственный символ, неверно. Если бы вам было достаточно одного символа, чёрточки были бы не нужны.
    
    Примитивы можно объединить либо контрактом, либо акцентом, но в любом случае примитив является единственным символом, обозначающим структуру.
    
    Это утверждение противоречит самому себе, "объединение" это и есть форма организации структуры. Получается, что как раз контракты или акценты задают структуру, а набор независимых примитивов никакую структуру не показывает.
    
    предлагаю отталкиваться от этого, и итерационно по одному дополнять, где и что вам видится не отвеченным.
    
    Извините, но я уже написал конкретные вопросы, и не вижу смысла повторять их еще раз. Вы не хотите на них отвечать, ок, будем считать, что вы уходите от ответа. Это хорошо показывает качество вашей теории. Хотите ответить, цитируйте вопрос, пишите ответ, а не заставляйте собеседника гадать, какую часть вашего текста на какой вопрос вы считаете ответом.
    
    Ramayasket Автор
    30.07.2023 21:32
    #25812596
    Если она представляет какую-то информацию, значит одного символа вам недостаточно, чтобы это выразить.
    
    "объединение" это и есть форма организации структуры. Получается, что как раз контракты или акценты задают структуру, а набор независимых примитивов никакую структуру не показывает
    
    Да это понятно, что символов больше одного. Речь шла о том, что существует единственный "самый простой" элемент, который формирует все более сложные абстрактные объекты -- нуль-система, и он отображается примитивом. Видимо, я криво выражался. Вы правы.
    
    Контракт состоит из трёх экземпляров нуль-системы. Коннектор это изобразительное средство. В классе contract никаких коннекторов нет, поэтому он и не входит в структуру контракта.
    
    P.S. Буду цитировать вопросы по одному и отвечать разными комментариями, чтобы не было простыней.
    
    michael_v89
    30.07.2023 21:32
    #25812874
    Еще раз, способ, которым примитивы формируются в структуру, это тоже один из базовых элементов. Вы выражались не криво, а логически неверно. Подумайте, в чем разница между двумя независимыми примитивами и одним сложным объектом из двух примитивов, как они различаются в вашей теории.
    
    Ramayasket Автор
    30.07.2023 21:32
    #25813012
    Я говорил "криво" про символы. В данном же случае я не понимаю, о чём дискуссия. Базовый элемент -- нуль-система. Более сложный объект -- контракт. Если он более сложный, значит уже не базовый.
    
    Контракт -- это способ создать следующий по сложности объект. Я кажется понял, что вы имеете в виду, говоря "базовый" -- что ещё более сложные объекты строятся с участием контракта. Но тогда любой более простой объект может называться "базовым" в отношении того, в чём он участвует, вы это хотели сказать?
    
    michael_v89
    30.07.2023 21:32
    #25813238
    +2
    Более сложный объект — контракт.
    Контракт — это способ создать следующий по сложности объект.
    
    Эти два утверждения противоречат друг другу.
    Если контракт это способ объединять примитивы в сложные объекты, то он сам не может являться сложным объектом, так как тогда непонятно, как мы этот сложный объект "контракт" получили без контракта.
    
    Я кажется понял, что вы имеете в виду, говоря "базовый" — что ещё более сложные объекты строятся с участием контракта.
    
    Говоря "базовый", я подразумеваю, что это синоним выражений "самый простой" и "примитив", о которых шла речь.
    
    В данном же случае я не понимаю, о чём дискуссия.
    
    Я написал об этом явно уже несколько раз. Способ задания связи между примитивами-кружочками это другой элементарный символ, который не определяется через примитивы-кружочки, поэтому символов вас не один, как вы утверждаете. Причем я сейчас обнаружил, что у вас таких способов целых два — одинарная черточка и двойная.
    
    На этом рисунке изображены только примитивы. Вам понятен характер связей между ними?
    
    Если нет, значит одних символов "примитив" недостаточно для задания сложных конструкций, нужны также другие символы.
    
    Это может быть так или так.
    
    А может и просто 9 отдельных примитивов.
    
    Вы утверждали "Только вот язык, который используется, включает в себя единственный символ". Это утверждение неверно. Символы вашего языка это кружочек-примитив, одинарная черточка-коннектор, двойная черточка-коннектор, и другие. И если они записаны в абстрактной памяти, они точно так же нуждаются в интерпретации.
  1. Ramayasket Автор
    30.07.2023 21:32
    #25813104
    Кварки не играют роль памяти, кварки это тоже смешанная система со всеми тремя элементами
    
    Если вам известны элементы, составляющие кварк, срочно публикуйтесь.
    
    А если серьёзно, кварк сам по себе не меняет цвет. Он не может быть смешанной системой. Для изменения цвета требуется глюон. Глюон также не меняет информацию о цвете в самом себе -- только в кварках.
    
    Кварки это фермионы, глюоны переносчики взаимодействия -- бозоны.
    
    Поэтому именно кварки и глюоны, работающие совместно, образуют смешанную систему.
    
    Больше того, вопрос устройства кварков и глюонов выходит за рамки статьи и её обсуждения. Они упомянуты для иллюстрации функций хранения и изменения, возникающих в природе. Вы же не будете спорить, что эти функции присутствуют в системе кварк-глюон?
    
    michael_v89
    30.07.2023 21:32
    #25813314
    Если вам известны элементы, составляющие кварк, срочно публикуйтесь.
    
    Мы говорили про элементы, которые указываете вы — память, время, объекты в памяти, а не про физические составляющие кварка.
    
    Вы же не будете спорить, что эти функции присутствуют в системе кварк-глюон?
    
    Я спорю с утверждением про глюоны. Вы сказали, что они являются временем для кварка, но у глюона тоже есть память и записанное в ней состояние, поэтому отдельным компонентом они являться не могут.
    
    Физические глюоны на самом деле взаимодействуют между собой, но в рамках аналогии это действительно не важно.
    
    Теперь стало понятнее, что под выражением "система имеет время" вы понимаете не возможность изменения, а набор фактических изменений. Я не могу сказать, что согласен с этим, но тут надо рассматривать неучтенную сущность "физические законы взаимодействия", это уже оффтоп.

Композиция математических объектов в рамках абстрактной модели мышления +8

Аннотация

1. Введение

2. Парадигма

3. Структура АММ

4. Абстрактные объекты

5. Темпоральная механика

6. Движения

7. Математические понятия

8. Множества

9. Заключение

Список литературы

Комментарии (150)

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор

Ramayasket Автор