В комментариях к моей статье о вычислительной сложности игр и в личных беседах проявился явный интерес к поведенческим играм антагонистической природы, однако тут не всё так просто. Такие игры несут значительную вероятностную нагрузку и простые подходы к сложности неприменимы (прошу прощения за каламбур). Тем не менее многие игры такого характера также не раз становились предметом исследований, в результате которых были разработаны математические модели этих игр.

В сегодняшней статье речь пойдёт об игре, о которой я, к своему стыду, узнал всего лет пятнадцать назад, хотя она появилась ещё в 1986 году и стала достаточно популярной уже в середине 90-х. Сегодня найти человека, который ничего не знал бы об этой игре, практически невозможно. Я говорю о «Мафии».

«Мафия» — клубная командная психологическая пошаговая ролевая игра, созданная в 1986 году студентом МГУ Дмитрием Давыдовым, базируется на культурно-исторической теории советского психолога Л. С. Выготского. В Википедии достаточно подробно описана сама игра и её варианты, но существуют и классические правила.

В общем, различные варианты игры похожи, и все участники разделены на две конкурирующие фракции: красная команда — «мирные жители», чёрная команда — «мафия». Цель игры состоит в том, чтобы уничтожить группу противника. Игра состоит из двух последовательных фаз (дневной и ночной) и определённого набора действий. Члены мафии обладают определёнными фичами (знают друг друга, убивают ночью), тогда как «мирных жителей» больше. Оказывается, что относительно небольшое количество членов «мафии», т. е. пропорциональное квадратному корню из общего числа игроков, даёт равные шансы на выигрыш для обеих групп. Кроме того, игра сильно зависит от чётности общего числа игроков.

Как я уже писал, существует множество вариантов игры. Типичная модификация игрового процесса заключается в добавлении персонажей с особыми способностями. Например, два особых мирных жителя могут быть «шерифом» (каждую ночь проверяет, состоит ли выбранный человек в мафии) и «врачом» (может защитить жертву от убийства, если сделает правильный выбор). В этой статье проанализируем простейшую версию игры без каких-либо специальных игроков или дополнительных правил. Пусть это и не самый популярный вариант, но для математического моделирования он лучший. Несмотря на то, что «Мафия» имеет сложную психологическую составляющую, возможно создание стохастической модели игры. То есть ориентируемся на игру, в которой убийства происходят случайным образом, а решения не зависят от хода предыдущей игры. Это очень большое упрощение, и оно будет применяться только тогда, когда участники не смогут наблюдать за поведением других или использовать эту информацию. Однако даже такая базовая модель даёт нетривиальные результаты. Итак, рассмотрим игру, начинающуюся с n игроков, из которых m члены мафии.

Основные вопросы, требующие решения:

• Какова вероятность того, что мафия выиграет w(n, m)?

• Как будет развиваться игра? То есть, какова вероятность того, что через заданное время останется ровно определённое количество членов мафии?

Помимо прямых ответов (т. е. выражений в замкнутой форме), рассмотрим приближения, качественное поведение и некоторые частные случаи. Предыдущих исследований игры совсем немного. Ранее была выведена простая асимптотическая формула шанса на победу мафии:

В этой статье предлагается развитие этой модели.

Большинство исследований концентрируются на психологическом аспекте игры, в частности — на обмане. Часто анализируемые темы включают в себя изучение невербальной семиотики, голосовых параметров и лингвистических особенностей. Интерес к исследованию этой игры мотивирован как математикой, так и психологией. Экспериментальные отклонения от идеализированного поведения дают ценную информацию о психологии выбора стратегии, манипулирования и сокрытия личности.

Прежде чем перейти к математике, необходимо записать произвольно выбранные правила игры. Некоторые предположения сделаны для упрощения модели, другие — исключительно для удобства.

Сеттинг

• Для игры нужны n игроков и «мастер» для координации действий и ведения игры.

• Вначале игроки случайным образом делятся на (n – m) мирных жителей и m мафиози.

• Члены мафии знают личности друг друга, мирные жители — только свои.

• Есть две чередующиеся фазы, день и ночь, которые вместе составляют ход.

• В течение дня есть два последовательных этапа:

  • Дебаты. Каждый оставшийся в живых может сказать что-либо, связанное с обвинением или защитой.

  • Голосование. У каждого есть один голос за то, кого следует линчевать. Игрок, набравший наибольшее количество голосов, выбывает (в случае ничьей выбывает случайный «победитель»). Фракция жертвы раскрывается.

• В течение ночи:

  • Мафия совместно решает, кого они хотят устранить.

• Игра продолжается до тех пор, пока не останется только одна фракция.

Короче говоря, днём выбывает один игрок (мирный житель или член мафии), тогда как ночью мафия стопроцентно убивает одного мирного жителя. Следовательно, за один ход возможны следующие количественные изменения: (n, m) → (n – 2, m) и (n, m) → (n – 2, m – 1). Их вероятности в принципе зависят от n, m и хода игры (т. е. предыдущих дебатов и голосований). Для начала формирования математической модели нам необходимо избавиться от психологического аспекта, ограничившись лишь стратегической и вероятностной частями игры.

Это грубое приближение, поскольку психология играет очень важную роль в этой игре. Тем не менее даже такая голая модель имеет интересные свойства. Более того, стоит пренебречь и фазой дебатов, поскольку её крайне сложно формализовать осмысленным способом. Теперь давайте приведём аргументы, почему вероятность перехода зависит только от текущего состояния (n, m). Рассмотрим сценарий, в котором игроков линчевали случайным образом. Жертва линчевания является членом мафии с вероятностью m/n, поэтому

Обозначим через w(n, m) шанс победы мафии при случайных линчеваниях, вызванный указанными выше вероятностями. Предположим, что существует оптимальная стратегия для мирных жителей, дающая w'(n, m) < w(n, m). Тогда мафия может устроить случайное линчевание, притворяясь мирными жителями, то есть действуя во время дебатов и этапов голосования так же, как это делают гражданские. В таком случае:

• Каждый член мафии информирован лучше, чем любой мирный житель.

• Выявить члена мафии со 100%-ной вероятностью невозможно.

Имейте в виду, что второй пункт работает только в игре без психологической части, когда ни схема голосования, ни поведение не выдают фракции. Например, никто не покраснеет, когда его обвинят в принадлежности к мафии. Предположим, что существует оптимальная стратегия для мафии: w''(n, m) > w(n, m). Если мирные жители в большинстве, они могут форсировать выборочное линчевание, выполнив следующую процедуру:

• Один из них говорит: «Пусть каждый из нас задаст число k_i от 1 до n, мы ликвидируем игрока»:

• Это число является случайным, как и выбранный игрок.

• Каждый мирный житель проголосует за выпавший номер.

• Поскольку мирных больше, чем членов мафии, голоса мафии не играют никакой роли.

Если мирные жители находятся в меньшинстве (т. е. m > n – m), независимо от того, каковы будут ходы, мафия победит. Предположим, что в случае m = n – m, линчевали случайного игрока. Если использование явной случайности не запрещено — вместо вычисления случайного игрока жребий может быть произведён каким-то другим образом (например, с помощью игральных костей). Случайная казнь является вполне оправданной стратегией. Конечно, в реале было бы очень скучно играть таким образом, но поскольку мы отбросили психологическую сторону, мы пренебрегаем и скукой. Более того, даже если игроки не линчуют наугад, эффективный выбор может привести к вероятности, сходной с вероятностью идеализированной модели. Как прямое следствие (1), шанс победы мафии может быть выражен в виде рекуррентного уравнения:

Приведённое уравнение является основой статьи. Исследуем его для одного члена мафии, его качественное поведение и решение в замкнутой форме, а также асимптотическую формулу. Важно отметить, что можно ставить разные граничные условия. То есть в уравнении (2) мы можем написать (1, если m ≥ n — m) вместо (1, если m > n — m). В этом случае все результаты можно воспроизвести, в несколько изменённом виде.

Игра с одним членом мафии

Для начала рассмотрим самый простой случай — игру с одним членом мафии. То есть, анализируем w(n, 1). В игре с одним членом мафии вероятность его победы равна вероятности того, что при каждом линчевании ликвидируют мирного жителя. Учитывая, что мы начинаем игру с дневной фазы, получаем:

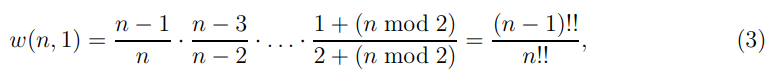
где n!! является двойным факториалом n. Приведённая выше формула имеет явную зависимость от чётности n. Хотя очевидно, что добавление двух мирных жителей снижает шансы мафии на победу w(n + 2, 1) < w(n, 1), в случае добавления одного – это не так. Фактически, добавление ещё одного игрока (при m = 1) увеличивает шанс на победу мафии. Чтобы понять это, давайте воспользуемся примером. В игре с одним мирным жителем и одним членом мафии голосование равное, поэтому линчевание основано на простом жребии, типа подбрасывания монеты и w(2, 1) = 1/2. В игре с двумя мирными жителями мафия также побеждает, линчевав гражданского (второго нужно убить ночью). На этот раз за мафией охотиться сложнее, и w(3, 1) = 2/3. Можно подумать, что мы столкнулись с проблемой граничных условий (т. е. убийство случайного игрока при ничьей). Это не так. Можно легко проверить, заменив (1, если m > n – m) на (1, если m ≥ n – m) в (2), при этом мы получим одинаковый результат. Проверка показывает, что добавление нечётного игрока всегда увеличивает шансы мафии на победу. Докажем это, используя в качестве основы w(3, 1) > w(2, 1). Тогда для индуктивного предположения w(2k + 1, 1) > w(2k, 1) нужно показать, что w(2(k + 1) + 1, 1) > w(2(k + 1), 1):

Методом математической индукции мы доказали, что w(2k + 1, 1) > w(2k, 1) для любого k > 0.

Рассмотрим w(n, 1), усреднённое по соседним числам. Используем среднее геометрическое, так как оно упрощает результат:

Усреднение можно рассматривать как приближение, в котором получаем монотонную функцию. Чтобы получить некоторую информацию о зависимости w(n, 1) от чётности n, рассмотрим следующее соотношение:

Вышеприведенное выражение имеет предел, когда k стремится к бесконечности, который можно найти с помощью формулы Валлиса:

Исходя из полученных результатов, можно сформулировать приблизительные шансы победы мафии, учитывающие равенство количества игроков:

Или, учитывая (n + 1)/n → 1,

Как видно, рекуррентное уравнение даёт противоречивые результаты. Представьте, что игроков четверо с одним членом мафии. Его шанс на победу равен w(4, 1) = 3/8 = 0,375. Затем приглашаем ещё пятерых игроков к фракции мирных жителей, тогда шансы выигрыша мафии возрастают до w(9, 1)=128/315=0,406 (вопреки наивным ожиданиям).

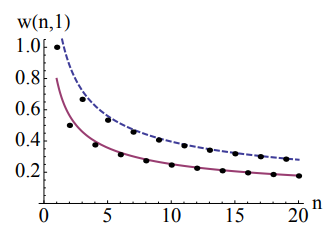
Качественные свойства w(n, m)

Учитывая удивительный эффект от добавления дополнительного мирного жителя в игру с одним членом мафии, естественно, возникает ещё несколько вопросов:

• Увеличивает ли добавление двух мирных жителей их шанс на победу, т. е. w(n + 2, m) < w(n, m)?

• Как влияет добавление одного мирного и одного члена мафии на вероятность выигрыша мафии, т. е. w(n + 1, m + 1) > w(n, m)?

• Уменьшает ли переход одного игрока из фракции мафии во фракцию мирных шанс мафии на победу, т. е. w(n, m + 1) > w(n, m)?

На самом деле, приведённые выше вопросы эквивалентны, в чем мы можем убедиться, используя рекуррентное соотношение из (2):

для n − m ≥ m > 0 после некоторых косметических арифметических действий получим:

Эти отношения могут быть переведены в:

Помимо эквивалентности «очевидных» неравенств нас интересует, выполняются ли они. Воспользуемся третьей частью (11) как гипотезой, сформулировав её следующим образом:

Если члена мафии обращают в добропорядочного гражданина, шанс на победу мафии не увеличивается, то есть w(n + 1, m + 1) ≥ w(n + 1, m). Если дополнительно n – m ≥ m неравенство сильное, w(n + 1, m + 1) > w(n + 1, m). Введём в игру с n игроками дополнительного персонажа. «Агент» — это дополнительный игрок, обычно имитирующий члена мафии. Покажем, что «агенту» необязательно раскрывать свою личность до самой поздней части игры.

Поскольку мирные жители неразличимы, давайте предположим, что мафия убивает их ночью в фиксированной последовательности. Пусть у агента будет последняя позиция в последовательности. Во время линчевания есть три варианта:

• Погибает мирный житель.

• Погибает член мафии.

• Погибает агент.

В случае смерти агента его принадлежность не имеет значения. В двух оставшихся ситуациях игра продолжается с агентом. Принадлежность агента играет решающую роль в двух ситуациях:

• Когда все члены мафии мертвы.

• Когда остается 0 или 1 мирный житель и 1 или 2 члена мафии.

В реальной игре предыдущее голосование агента может иметь значение для установления или разрыва связей, не говоря уже о фазе дебатов. Но случайное голосование (мы ввели для моделирования) сводит на нет все эти соображения. В обоих случаях, когда агент является членом мафии, шансы на победу мафии увеличиваются:

Общий шанс победы мафии равен среднему шансу выигрыша, усреднённому по непересекающимся играм. Вес — это вероятность достижения такой игры. Изменение принадлежности агента не влияет на веса, но в финале всегда увеличивает шанс на победу мафии, w(n + 1, m + 1) ≥ w(n + 1, m), что доказывает нашу первую гипотезу. Кроме того, в случае игры, в которой все члены мафии убиты, принадлежность агента также играет роль, следовательно, w(n + 1, m + 1) > w(n + 1, m), а это вторая гипотеза.

В случае, когда n – m ≥ m добавление нечётного игрока всегда увеличивает шанс выигрыша мафии, а не только в играх с одним членом мафии (4). Индуктивное предположение говорит о том, что это свойство справедливо для общего числа игроков n ≤ 2k + 1:

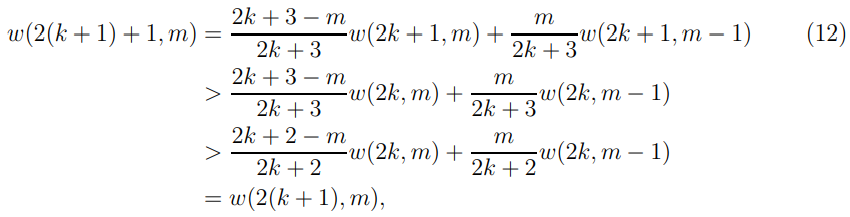
где используем ранее доказанную связь w(2k, m) > w(2k, m – 1) и тот факт, что (при усреднении двух компонент) придание меньшего веса большему члену приводит к уменьшению суммы.

Эволюция

Выше мы рассматривали шансы выигрыша мафии относительно начального числа игроков N и членов мафии M. Может быть интересно исследовать динамику игры, то есть проанализировать вероятность p_m(t) того, что после t хода в мафии останется ровно m членов. Хотя это выходит за рамки уравнения (2), всё равно является прямым следствием модели случайного линчевания (1). Заглавные буквы N и M используются для обозначения начальных условий. Каждый ход (день + ночь) убивает двух игроков, поэтому общее количество игроков уменьшается n(t) = N – 2t.

Дискретное время

Эволюция каждого p_m(t) определяется набором рекуррентных уравнений

где m принадлежит множеству натуральных чисел и с начальным условием p_m(0) = δ_mM.

Вышеописанный случайный процесс с M + 1 различными состояниями и (m) → (m – 1) является марковским. А этот конкретно называется чистым процессом смерти (подкласс процессов рождения и смерти). В нашем случае вероятности меняются со временем, что является небольшим осложнением.

Важно отметить, что уравнение (13) верно только тогда, когда m ≤ n(t), то есть когда жив хотя бы один мирный житель и в игру ещё можно играть, в противном случае оно не имеет смысла. Но почему ошибочное уравнение для m > n(t) не портит состояния с m ≤ n(t)? Пусть для данного времени t p_m(t) — вероятность ошибки с наименьшим индексом, т. е. m = N − 2t + 1. На следующем ходу это влияет на p_{(m − 1)}(t + 1). Но теперь наименьший ошибочный индекс равен N − 2(t + 1) + 1 = m − 2 < m − 1. Значит, ошибка распространяется медленнее, чем исключение состояний.

Решение в закрытой форме для p_m(t) имеет вид:

Пример изображён на левом рисунке ниже. Выражение, приведённое выше, хотя и является точным, всё же довольно сложное. Проанализируем среднее количество игроков в мафию через t дней и ночей, т. е.

В процессах рождения и смерти с переходными коэффициентами, пропорциональными метке состояния (как процесс радиоактивного распада или процесс Юла), такое среднее значение может быть получено путём прямого расчёта с использованием (13):

Результат верен только тогда, когда N − 2t − M ≥ 0, то есть среднее берётся по вероятностям правильных состояний.

Аппроксимация непрерывного времени

Обычно дифференциальные уравнения проще разностных. Грубо аппроксимируем эволюцию в дискретном времени (13) её версией с непрерывным временем.

Поменяем в (13) разность p_m(t + 1) – p_m(t) на дифференциал

где m принадлежит множеству натуральных чисел и с начальным условием

Когда относительное изменение производной функции происходит в интервале единичной длины [t, t + 1], аппроксимация должна быть

Интуитивно говоря, когда вероятность линчевания члена мафии в течение дня невелика, такое приближение оправдано. Однако в рамках данной статьи оценку погрешности аппроксимации проводить не будем. Решение дифференциального уравнения (18) имеет вид:

С этим удобнее работать, чем с выражением (14). Пример представлен на предыдущем рисунке слева. Например, легко находятся максимумы.

Среднее число членов мафии, определенное в (15), равно

что является более простым выражением, чем его аналог (16). Сравнение формулы дискретного времени с её аппроксимацией непрерывного времени представлено на предыдущем рисунке справа. Оценим выигрышные шансы мафии. Поскольку

это вероятность того, что мирные жители выиграют, установка времени, в течение которого останется только один игрок, даёт общий шанс мирных на победу:

Неудивительно, что в аппроксимации непрерывного времени явная зависимость от чётности отсутствует (дискретные свойства теряются).

Общее решение

Результат для p_m(t) (14) не только интересен сам по себе — он также даёт решение для определения выигрышного шанса мафии (2). Напомню, что p₀(t) — это вероятность того, что после t ходов мирные жители выиграют. Когда общее количество игроков нечётное, игра длится t_odd = (N – 1)/2, в результате чего в живых остаётся 1 игрок. Таким образом, p₀(t_odd) — это вероятность того, что мирный житель выиграет игру. Для чётного числа игроков после t_even = N/2 ходов в живых не останется никого. Но p₀(t_even) — это вероятность того, что мафии нет, то есть фактически за последнюю ночь никто не был убит и мирный житель выиграл. Итак,

Следовательно, формула закрытой формы для расчёта победного шанса мафии:

Давайте посмотрим на асимптотическое поведение (9), которое было доказано выше для игры с одним членом мафии. Чтобы получить асимптотическую формулу для w(n, m), достаточно заметить, что в пределе n→∞  и вклад вносят только первые два члена суммы. Для i = 0 член равен 1. Члены с i > 1 не имеют значения, поскольку (n – i)!!/(n – 1)!! → 0. Следовательно, можем написать

используя результат игры с одним членом мафии, то есть, аппроксимируя (3) с помощью (9). Приблизительную формулу (24) формально можно выразить как

Интересно выяснить оптимальное количество членов мафии для заданного количества игроков. Игра интересна, прежде всего, тогда, когда обе противоборствующие фракции имеют равные шансы на победу, изображённые на графике ниже.

На самом деле это всего лишь приблизительный аргумент, поскольку мы применили асимптотическую формулу к конечному n, не исследуя, как сходимость зависит от m.

В каждой практической игре в мафию есть психологическая часть, которую в начале статьи мы договорились не затрагивать. Сухая математическая модель может стать достаточно сложной основой, но её явно недостаточно для описания реальной игры. В ходе игры мирные жители получают некоторую информацию — либо самостоятельно узнавая личность другого человека, либо перехватывая какие-то сообщения. Более того, голосование может быть обусловлено чисто эмоциональными оценками. К тому же нельзя недооценивать харизму и убедительность отдельных игроков, способных оказывать на других серьёзное влияние.

Все эти процессы можно попытаться как-то оцифровать и исследовать математически, однако по-прежнему остаётся много проблем в поиске подходящей модели. В любом случае теория должна коррелировать с экспериментом. Исходя из личного опыта, игра малознакомых игроков более непредсказуема в отличие от игры хорошо знакомых людей. Эта разница как раз и вытекает из психологических аспектов игры, поэтому моделирование реальной игры без упрощений практически неосуществимо, но, возможно, в этом и заключается секрет успеха игры, начавшей свой путь из тесной комнаты студенческой общаги.

НЛО прилетело и оставило здесь промокод для читателей нашего блога:
-15% на заказ любого VDS (кроме тарифа Прогрев) — HABRFIRSTVDS