
Многие задачи, с которыми мы имеем дело при цифровизации производства (неважно какого), – это задачи оптимизации: оптимизация производственного расписания, оптимизация цепочек поставок и размещения объектов, оптимизационное планирование и прочее. Многие из них сводятся к проблемам смешанного линейно-целочисленного типа (MILP – Mixed Integer Linear Problem). Конечно же мы хотим их решать быстрее и эффективнее, поэтому год назад начали разработку ML-модулей для этого. В этой статье мы познакомим вас с концептом одного такого модуля – для упрощения MILP методом обнуления переменных – и расскажем о том, насколько нам удалось с его помощью сократить время работы решателя.
Но сначала давайте коротко объясним, откуда ноги растут у идеи применения ML для MILP.
Ремарка. Мы в этой статье – это я и мой коллега Александр Подвойский. Вместе мы работаем над ML-моделями для MILP. Далее в отношении задач/проблем типа MILP мы будем использовать термин «проблема», так как он более устоявшийся.
Зачем нам ML
Обычно для решения MILP используются решатели вроде Gurobi и Cplex. Сами эти инструменты невероятно сложны, но принцип их применения прост:
Пользователь формулирует проблему: ограничения, целевую функцию, описание переменных (вещественные/целочисленные/бинарные).
Такая проблема поступает на вход решателю, который, применяя заложенные в нем эвристики и методы оптимизации (линейные и целочисленные), пытается найти допустимое решение, при этом оптимизирует (обычно решается задача минимизации) заданную целевую функцию.
Компании-создатели этих решателей постоянно улучшают свои продукты[1], но в производстве встречаются проблемы, обработка которых даже при использовании самых продвинутых решателей занимают много времени. Чтобы ускорить их обработку, ряд исследователей экспериментируют с различными техниками машинного обучения. Мы тоже решили попробовать.
ML-техники для ускорения решения MILP можно разделить на две группы. Первая направлена на проблему, а именно – на «упрощение» проблемы. Вторая – на решатель, то есть на повышение его (решателя) эффективности.

Как уже отмечалось, здесь мы поговорим про первую группу – будем «упрощать» проблему, чтобы решатели, а мы будем использовать решатель SCIP[9] версии 8.0.3 (SoPlex 6.0.3)*, смогли обработать ее быстрее и/или с лучшим значением целевой функции.
*Мы бы использовали Gurobi, Cplex или какой-либо другой хороший зарубежный коммерческий инструмент схожей функциональности, но их уже как два года невозможно купить в России. Для разработки же отечественного решателя сравнимой производительности потребуются усилия целой научной группы и много времени. Так что работаем с некоммерческим решателем SCIP, который показал лучшую производительность в наших задачах среди аналогичных доступных инструментов.


Для упрощения каких проблем мы создаем ML-модель
Сразу оговоримся, мы не ставили перед собой цель построить ML-модели общего назначения, которые можно было бы применить для сокращения размерности (упрощения) любой проблемы, относящейся к MILP, а сосредоточились на определенных, часто нам встречающихся типах проблем, а именно:
Оптимизация цепочек поставок.
Пример типичной постановки: пусть есть множество складов, на которых хранятся некоторые продукты, есть ограничения на объемы хранения, есть склады, на которые эти продукты с первого склада необходимо переместить, есть график поступления продуктов на склады хранения, есть мощности по перемещению продуктов. Необходимо составить оптимальный (или хороший, или приличный) график перемещения продуктов на склады.
Оптимизация смешений компонентов для получения продуктов.
Пример типичной постановки: есть множество компонентов, множество установок смешения, множество резервуаров, в которых должны быть смешаны продукты из данных компонентов, топология труб с пропускными способностями, насосы, перекачивающие компоненты по трубам из резервуаров. Необходимо смешать заданное количество продуктов за минимальное время.
Оптимизация работы установок по переработке нефтепродуктов.
Пример типичной постановки: есть множество установок, есть режимы работы таких установок, есть потоки материала на входе в установки. Необходимо выбрать режим работы каждой установки таким образом, чтобы произвести требуемое количество продукта за минимальное время.
Как упрощать? Концепт двухшагового решателя MILP
Представьте, что нам удается заранее, еще до применения решателя, с высокой точностью определять значения некоторых целочисленных переменных. Это позволило бы снизить размерность решаемой проблемы и упростить ее... Но это неточно*.
*На самом деле это действительно неточно. Казалось бы, чем меньше переменных и ограничений, тем проще решать систему уравнений. Но анализ сценариев из библиотеки MIPLIB показывает, что размерность проблемы слабо коррелирует со временем ее обработки решателем (то есть не всегда меньшая размерность ведет к быстрому решению и наоборот). Вообще, мы пока еще только ищем способ, как оценивать сложность проблемы без ее непосредственного решения, ориентируясь только по некоторым быстровычисляемым признакам типа количества переменных, плотности матрицы ограничений и т.д.
Однако для наших случаев это, как мы убедились, работает. Мы заметили, что многие задачи, такие как составление расписаний, оптимизация цепочек поставок и др., содержат большое количество бинарных и целочисленных переменных, и лишь небольшая доля этих переменных принимает ненулевое значение в окончательном решении. Это происходит из-за того, что большая часть наших переменных – технические, они нужны только для формулировки проблемы (например, для формулирования условия «один выполняет только одну задачу в каждый момент времени» обычно создается массив бинарных переменных для этого специалиста по числу задач и ставится условие, что сумма этих бинарных переменных в каждый момент времени <= 1). Если мы сможем еще до решения проблемы «занулить» большое количество таких переменных, то существенно снизим размерность задачи, а значит решим ее быстрее.
Наша концепция решения проблем типа MILP с предварительным обнулением переменных реализована в нашем решателе ZyOpt и описана в инфографике на Рисунке 1.
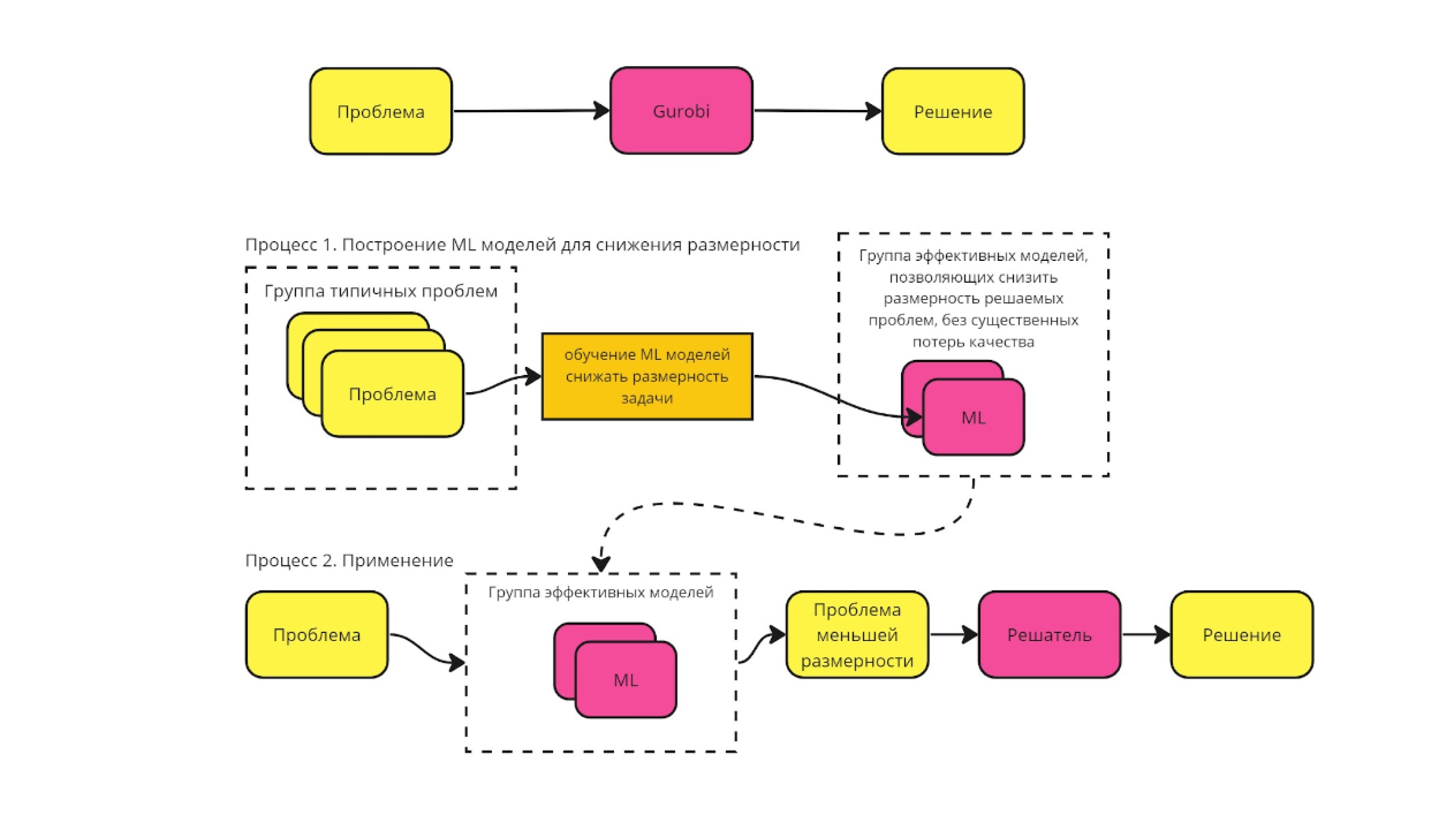
Итак, изначально мы имеем некий пул проблем и хотим собрать пайплайн, включающий в себя решатель, такой, чтобы он решал типичные проблемы (похожие на проблемы из данного пула) максимально эффективно. Для этого мы:
Решаем все проблемы из пула. Это происходит заранее, так что на это у нас есть достаточно времени.
Из полученных решений формируем обучающую выборку, которая представляет собой таблицу с колонками: имя переменной, проблема, значение, принятое в оптимальном решении, признаки для данной переменной.
На построенной выборке обучаем классификационную модель, которая будет классифицировать нулевые/ненулевые переменные бинарные/целочисленные переменные.
Теперь на этапе решения мы можем взять проблему со всеми переменными из нее и запустить на них наш классификатор. Фиксируем в 0 все нулевые переменные по результатам классификации.
Решаем решателем проблему меньшей размерности (с зафиксированными переменными) с надеждой, что это займет меньше времени.
Первый пункт – про решение всех проблем из пула – очевиден, и тут разбирать особо нечего. А остальные рассмотрим подробнее.
Обучающая выборка и обучение классификационной модели
Нам нужно было описать переменные, а точнее – построить для них признаковое пространство. Для этого мы разработали «Построитель признакового пространства» – лежит тут [3]. Он генерирует более 30 признаков для каждой переменной. Полный список признаков может быть найден тут [4]. Например, в число этих признаков входят значения коэффициента при переменной в целевой функции; количество ограничений, в которые переменная входит с отрицательным коэффициентом; количество клик, в которые входит переменная, и прочие.
Имея признаковое пространство, мы смогли произвести обучение с учителем. Для этого мы взяли множество проблем и их заранее найденные оптимальные решения. Имея оптимальные решения для каждой проблемы, построили бинарную разметку. В ней нулем отметили переменную, которая приняла нулевое значение в оптимальном решении, а единицей – все переменные, которые в оптимальном решении приняли ненулевое значение. Получив таким образом обучающую выборку, мы смогли перейти к классической части – обучению классификационной ML-модели.
Классификатор для предсказания значений переменных
Строго говоря, для прогнозирования значений переменных мы строили не классификатор, а регрессор (RandomForestRegressor или Ridge). Для решения самой задачи классификации мы устраивали отсечение – решали, что переменная примет нулевое значение, если значение этой переменной, восстановленное регрессором, не превышает некий заранее заданный порог.
Эксперименты, результаты которых приводятся ниже, выполнялись на проблеме смешения нефтепродуктов из компонентов. Все проблемы могут быть найдены тут [5].
Для кросс-валидации мы применили роторную схему:
Брали одну проблему из всего пула и исключали ее из обучающей выборки.
На оставшихся проблемах обучали модель-регрессор восстанавливать значения переменных.
С помощью этой обученной модели мы восстановили значения переменных для выбранной проблемы и зафиксировали в 0 все переменные, значение которых отличается от 0 не более чем на заданное пороговое значение.
Упрощение исходной проблемы и запуск решателя
Применив классификатор, мы получали набор нулевых переменных и изменили исходную постановку проблемы – добавили туда дополнительные ограничения на значение детектированных нулевых переменных, а проще говоря: xi= 0 для всех i из множества детектированных нулевых переменных.
Далее мы отправили проблему в новой постановке в решатель и сравнили время ее решения со временем решения исходной проблемы.
Результаты проведенных экспериментов представлены на Рисунке 2.
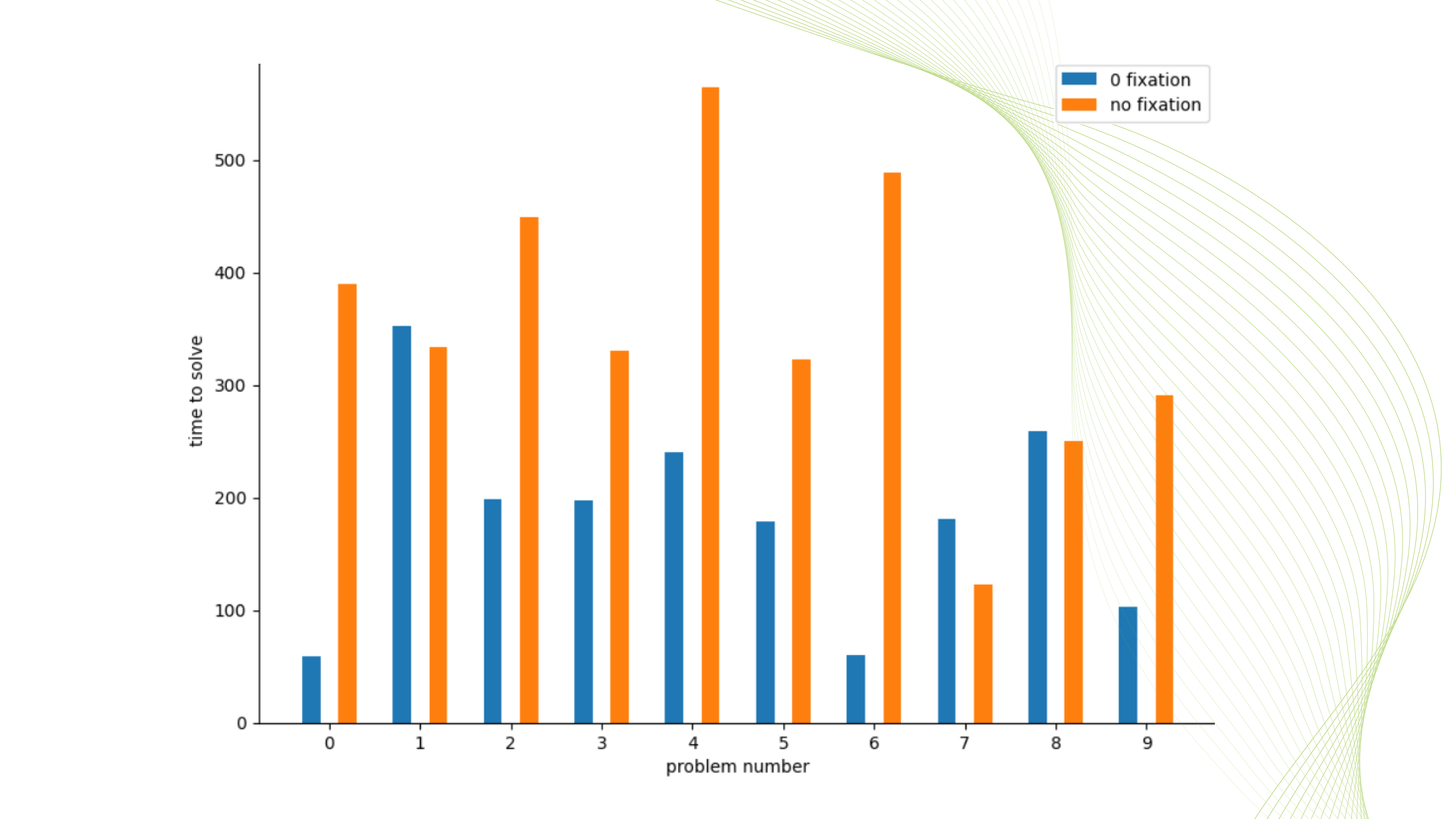
Как видно, в наших экспериментах с задачей смешения нефтепродуктов из заданных компонентов при фиксации нулей мы в среднем находили решение в два раза быстрее, чем без «обнуления», 8 из 10 проблем решились быстрее. При этом значение целевой функции не пострадало ни в одном случае, хотя в общем случае значение ЦФ при упрощении проблемы методом фиксации может деградировать по сравнению с оптимальным решением оригинальной проблемы. Но у нас порог фиксации был выбран не слишком агрессивный, поэтому деградации значения ЦФ не произошло. Если бы мы провели более агрессивное «обнуление», то могли бы получить еще более быстрое решение проблемы, но пришлось бы потерять оригинальный оптимум исходной (не упрощенной) задачи, а где-то, возможно, проблема стала бы неразрешимой.
На Рисунке 3 приведен пример работы классификатора для одной из проблем из нашего эксперимента (1664186663.lp). Видно, что регрессор не ошибся ни разу настолько, чтобы произошла ошибочная фиксация.
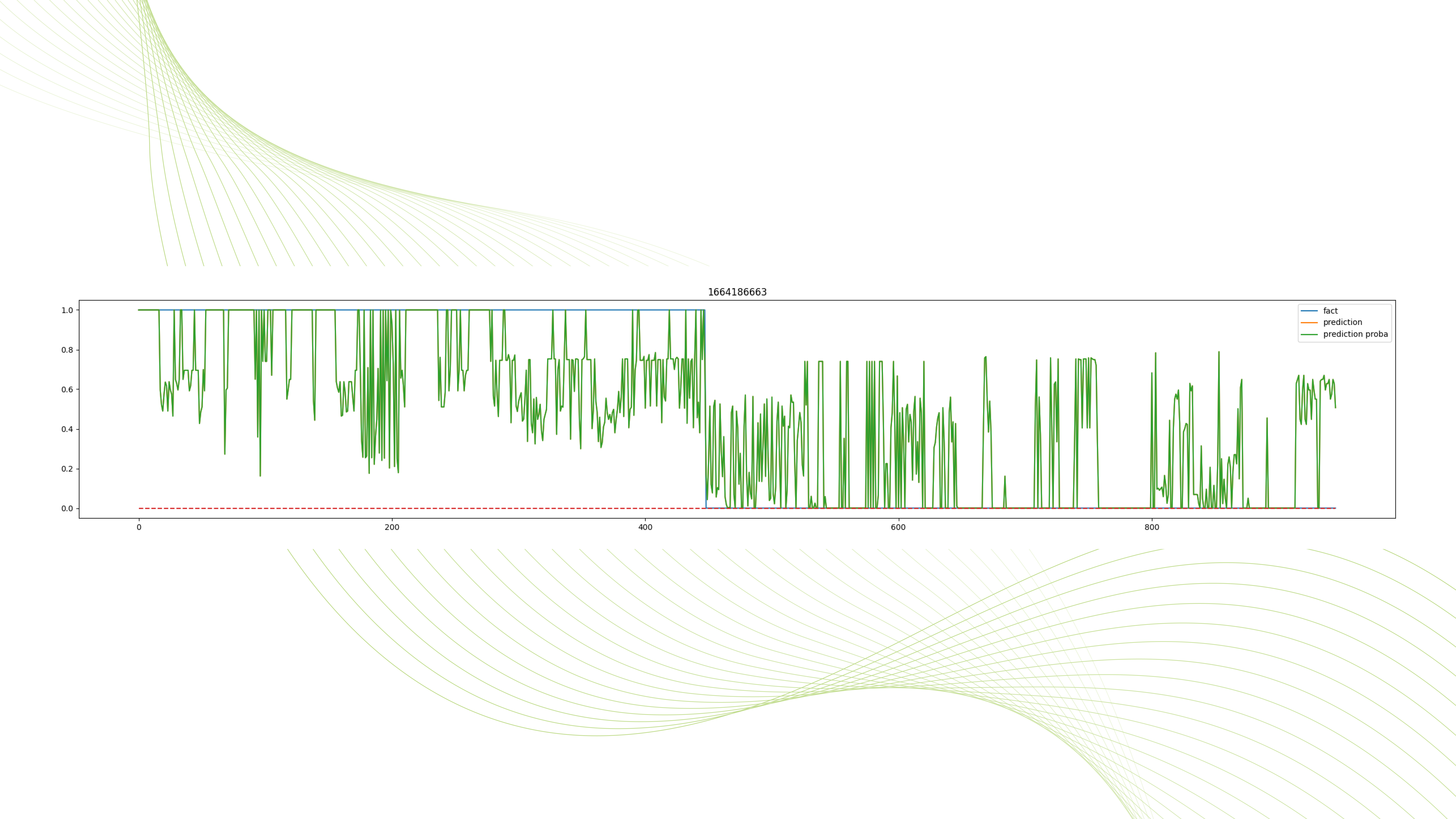
Далее мы решили углубить наш подход: нам хотелось заранее предсказывать не только нулевые, но и остальные значения для бинарных/целочисленных переменных. Мы знаем, что в задачах составления расписаний встречается большое количество бинарных переменных, и мы попробовали детектировать единичные значения для таких переменных и зафиксировать их, чтобы посмотреть, приведет ли это к ускорению решателя.
На Рисунке 4 приведены результаты эксперимента, аналогичного предыдущему, только на этот раз мы фиксировали не только нулевые переменные, но и единичные, т.е. ужесточили постановку задачи введением дополнительного ограничения xi=1 для всех переменных, которые были оценены регрессором более чем .99. В этом эксперименте мы получили ускорение по времени решения еще на 15%.
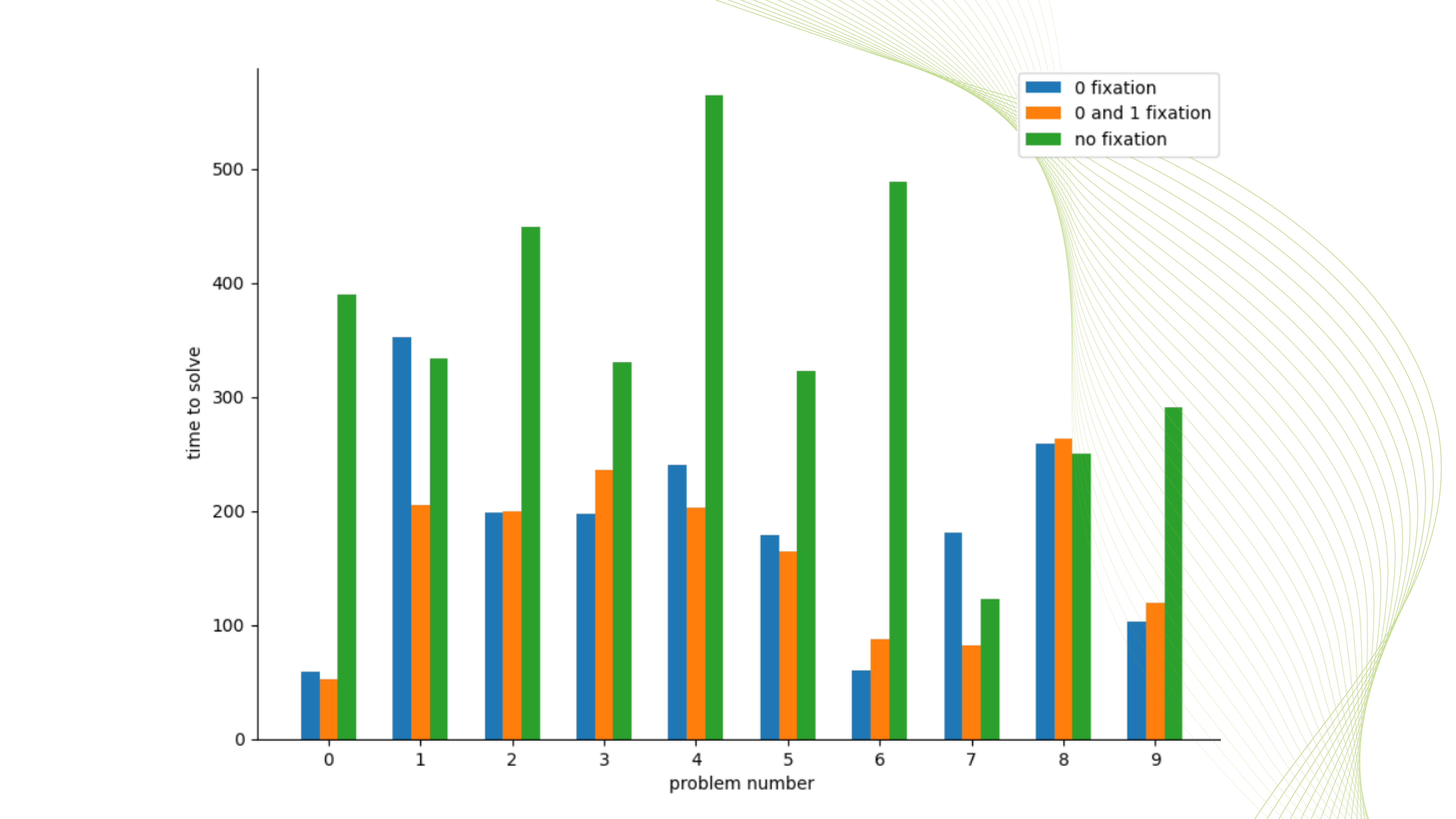
Итого, что дальше?
Как мы видим, применение представленной выше техники положительно сказывается на быстродействии решателя SCIP. Вообще, способы устранения «слабостей» постановки MILP кажутся наиболее перспективными по сравнению с другими способами повышения быстродействия MILP-решателей. Заметим так же, что предлагаемые в этой статье подходы не зависят от решателя и доменной области проблемы, что потенциально делает этот подход применимым в широком круге задач. В следующей статье мы разберем другие техники, основанные на ML-подходах, а именно – попытаемся детектировать ненулевые переменные посредством ансамбля детекторов аномалий.

