Перевод статьи Стивена Вольфрама (Stephen Wolfram) "The History and Future of Special Functions".
Выражаю огромную благодарность Кириллу Гузенко за помощь в переводе.

---

Статья представляет собой запись выступления, сделанного на Wolfram Technology Conference 2005 в Шампейне, штат Иллинойс, как часть мероприятия в честь 60-летия Олега Маричева.

Так, хорошо, сейчас я бы хотел вернуться к той теме, которую поднимал сегодня утром. Я бы хотел поговорить о прошлом и будущем специальных функций. Специальные функции были предметом моего увлечения как минимум последние 30 лет. И, полагаю, моя деятельность оказала весомое влияние в продвижении использования специальных функций. Однако, получилось так, что я никогда ранее не поднимал эту тему. Теперь пора исправить это.


История многих понятий и объектов математики прослеживается ещё со времён древнего Вавилона. Ведь ещё 4000 лет назад в Вавилоне была разработана и активно использовалась 60-ричная арифметика с различными сложными операциями.

В то время операции сложения и вычитания считались довольно простыми. Но это не касалось операций умножения и деления. И для того, чтобы производить подобные действия, были разработаны некоторые подобия специальных функций.

По сути, деление сводилось к сложению и вычитанию обратных величин. А умножение довольно хитрым образом сводилось к сложению и вычитанию квадратов.

Таким образом, практически любые вычисления сводились к работе с таблицами. И, конечно, археологам доводилось находить вавилонские таблички из глины с таблицами обратных величин и квадратов.

То есть у вавилонян уже была идея о том, что существуют некоторые кусочки математической или вычислительной работы, которые можно использовать многократно, получая весьма полезные результаты.

И, в какой-то мере, история специальных функций начинается с открытия принципов работы с последовательностями из этих самых «кусочков».

Следующие «куски» были, вероятно, теми, которые включают тригонометрию. Египетский папирус Ринда 1650-го года до н.э. уже содержал некоторые проблемы касательно пирамид, решение которых требовало тригонометрии. Стоит упомянуть, что была найдена вавилонская табличка с таблицей секансов.

Астрономы тех времён со своей моделью эпициклов, безусловно, уже вовсю использовали тригонометрию. И, опять-таки, все математические операции сводились к работе с небольшим количеством «специальных» функций.

Много внимания уделялось тому, что они называли хордами и дугами. Вот картинка.



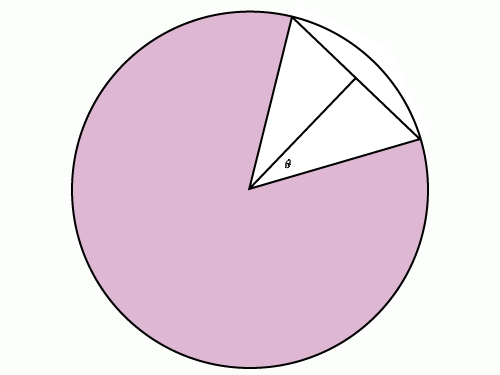
Имеются два радиуса единичной окружности с некоторым углом между ними. Какова длина хорды, заключённой между ними? Сейчас мы отображение угла в длину хорды называем функцией синуса угла.

И вот обратная задача: для некоторой длины хорды — каков будет угол? Несомненно, сейчас мы это называем арксинусом.

Греческие астрономы весьма серьёзно относились к этим своим хордам и дугам. Альмагест Птолемея полон их. И, говорят, около 140 года до н.э. Гиппарх собрал 12 томов с таблицами хорд.

Что ж, идеи о тригонометрии начали распространяться из Вавилона и Греции. Тригонометрия быстро обрастала различными стандартами и правилами. Гиппарх уже перенял у вавилонян представление о 360-градусной окружности.

И, от индийского слова «chord», буквально переведённого на арабский и затем неправильно переведённого на латынь, появилось слово «sine». Это было в 12-ом веке, а в начале 13-го века его активно начал использовать Фибоначчи.

В 14-ом веке тригонометрия получила широкое распространение. А в середине 16-го века она играла крайне важную роль в труде Коперника — De Revolutionibus. Данный труд на долгое время стал в своём роде фундаментальным для тех, кто работал с математическими функциями.

Именно тогда тригонометрия практически полностью обрела свой современный вид. Конечно, имеются несколько весомых различий. К примеру, постоянное использование версинуса. Кто-нибудь слышал вообще о таком? По сути, это 1 — Cos[x]. Вы можете найти его в тригонометрических таблицах, которые издавались до совсем недавнего времени. Однако сейчас парочка лишних арифметических операций — совсем не проблема, так что не стоит больше говорить об этой функции.

Что ж, после тригонометрии следующим большим прорывом были логарифмы. Они появились в 1614 году.



Это был способ свести умножение и деление к операциям сложения и вычитания.

В течение нескольких лет появилось множество таблиц с логарифмами. Использование таблиц, фактически, стало повсеместным стандартом, который просуществовал более трёхсот лет.

Потребовалось несколько лет, чтобы натуральный логарифм и экспонента обрели свою современную форму. Но в середине 17-го века появились уже все привычные нам элементарные функции. И с тех пор, вплоть до настоящего времени они являются, по сути, единственными явными математическими функциями, о которых большинство людей когда-либо узнаёт.

Что ж, получается, исчисление появилось в конце 17-го века. И это есть время, начиная с которого специальные в современном представлении функции начали появляться. Многие из них появились достаточно скоро.

Где-то в 18-ом веке одним из Бернулли была выдвинута идея, что, возможно, интеграл любой элементарной функции будет так же элементарной функцией. Лейбниц думал, что у него есть контрпример: 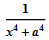. Однако это выражение таковым не являлось. В течение нескольких лет шли активные рассуждения об эллиптических интегралах. По крайней мере в терминах рядов. И так и были открыты функции Бесселя.

А к 20-м годам 18-го века Эйлер как раз начал погружаться в мир вычислений. И он писал о многих наших стандартных специальных функциях.

Он открыл гамма-функцию как развитие идеи факториала. Он определил функции Бесселя в некоторых приложениях, занимался эллиптическими интегралами, ввёл дзета-функцию, исследовал полилогарифмы.

Обычно он не давал функциям определённых названий.

Но постепенно всё больше и больше функций, о которых он писал, начинали использоваться разными людьми. И, зачастую, после некоторого периода их использования, они получали уже какие-то конкретные обозначения и имена.

Было ещё несколько всплесков активности в появлении специальных функций. В конце 18-го века были теория потенциала и небесная механика. И, например, функции Лежандра — которые долгое время назывались функциями Лапласа — появились около 1780 года. В 1820-х годах стал популярным комплексный анализ, и начали появляться различные дважды периодические функции. Нельзя сказать, что в те времена в этой сфере хорошо была налажена коммуникация между людьми. Так что в конечном итоге появились различные несовместимые обозначения для одних и тех же понятий. Проблемы, появившиеся тогда, актуальны и сегодня, и они зачастую служат поводом к обращениям в службу поддержки Mathematica.

Через несколько лет набрал обороты гармонический анализ, в результате чего появились различные ортогональные полиномы — Эрмита, Лейгра и так далее.

Что ж, уже в начале 19-го века было ясно, что появляется целый «зоопарк» специальных функций. И это заставило Гаусса думать о том, как всё это объединить.

Он исследовал гипергеометрические ряды, которые, фактически, были уже открыты в 1650-е Валлисом и названы в его честь. И он заметил, что функция 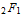(гипергеометрическая функция Гаусса) на самом деле охватывает множество известных специальных функций.

К середине 19-го века специальным функциям уделялось много внимания, особенно в Германии. В это время появилось множество литературы по данной тематике. Потому, когда Максвелл писал свои труды по электромагнитной теории в 70-х годах 19-го века, ему не приходилось много времени уделять математическому аппарату специальных функций; уже было множество литературы, на которую можно было сослаться.

Помимо чисто научных работ с описанием свойств функций создавались и таблицы с их значениями. Иногда людьми, о которых никто толком и не слышал. А иногда и весьма известными — в их числе Якоби, Эйри, Максвелл.

Так, задолго до конца 19-го века уже были созданы практически все специальные функции, с которыми мы имеем дело с сегодня. Но были и другие. К примеру, кто-нибудь слышал о том, что такое гудерманиан? Я помню, как встречал его в справочниках, когда был ребенком. Гудерманиан назван в честь Кристофа Гудермана, ученика Гаусса. Он устанавливает зависимость между тригонометрическими и гиперболическими функциями и тесно связан с меркаторовыми картографическими проекциями. Однако гудерманиан практически не встречается в современной литературе.

Что ж, большое количество интеллектуальных ресурсов было вложено в развитие специальных функций в последние несколько десятилетий 19-го века. Полагаю, всё могло развиваться в направлении теории инвариантов, сизигий или к каким-то другим характерным математическим устремлениям викторианской эпохи. И действительно, типичная любовь чистой математики к абстракциям и обобщениям сделала специальные функции произвольными и не особо связными. Это как изучать каких-то странных животных в зоопарке вместо того, чтобы изучать общую биохимию.

Однако прогресс в теоретической физике повторно активизировал интерес к специальным функциям. Механика. Теории упругости. Электромагнитная теория. Затем, в 20-х годах, — квантовая механика, в которой даже самые основные задачи требовали применения специальных функций, таких как многочлены Лагерра и Эрмита. А затем была теория рассеяния, которая, пожалуй, использовала практически весь «зоопарк» специальных функций.

Это породило мысль, что любая проблема в чистом виде каким-то образом всегда может быть решена в терминах специальных функций. И, без сомнения, учебники продвигали эту идею. Потому что обсуждаемые в них проблемы весьма лаконично формулировались в терминах специальных функций.

Конечно, были и некоторые пробелы. Многочлены пятой степени. Задача трёх тел. Однако они были слишком нестандартными. Не то, что требовалось для современных вероятностных теорий.

Вообще, сфера специальных функций весьма обширна. Создание таблиц набрало очень большие обороты, особенно в Англии. По-сути, данная сфера имела стратегическое значение государственной важности. В частности, для таких вещей, как навигация. Издавалось очень много таблиц. Вот, к примеру, неплохая подборка от 1794-го года. Когда я впервые их увидел, мне подумалось, что тут имеем место быть какой-то временной сдвиг.


(На самом деле этот Вольфам был офицером бельгийской артиллерии. Думаю, у меня с ним родства не больше, чем со святым Вольфрамом, который жил в 7-ом веке нашей эры).

Таблицы играли важную роль в то время, что вызвало появление разностной машины Бэббиджа в 1820-х годах, которая была предназначена для составления точных таблиц. И к концу 19-го века специальные функции являлись основой для их составления.

Механические калькуляторы становились всё более популярными, а в Британии и США были масштабные проекты по созданию таблиц специальных функций. К примеру, как проект WPA (Works Progress Administration project) в 30-е, когда во времена Великой депрессии людей занимали вычислением значений математических функций.

Тогда началась серьёзная работа по систематизации их свойств. У каждого было много работы, однако вклад каждого был не особо большой. Хотя все думали, что играют важную роль. Кстати, вот обложка американского Jahnke and Emde, который впервые был издан в 1909-ом году, а в 30-ом обзавёлся иллюстрациями.



И весьма недурными, между прочим.



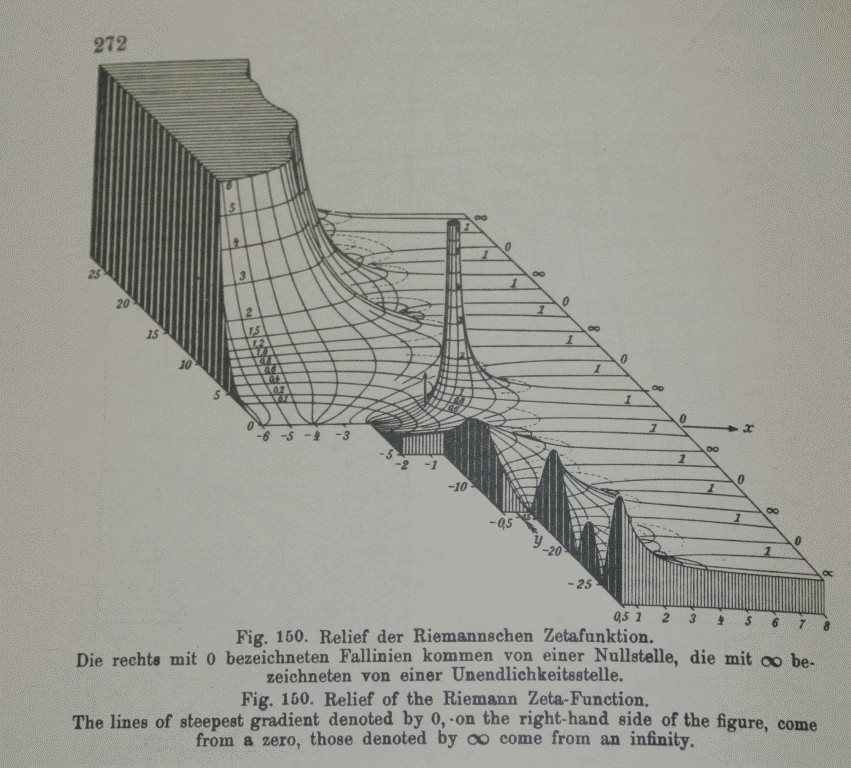
В начале 20-го века популярным было создание объёмных моделей функций из гипса и дерева. И да, у меня возникла идея для иллюстрации дзета-функции, которую я использовал для обложки первого издания The Mathematica Book от Jahnke and Emde.



Во время Второй мировой войны проводилось множество исследований по специальным функциям, и сложно объяснить — почему. Вероятно, это было вызвано какими-то военными нуждами. Хотя, я склоняюсь к тому, что это было просто совпадение. Однако потенциальную связь с какими-то стратегическими мероприятиями не следует отметать.

И вот, первое издание Magnus and Oberhettinger было опубликовано в 1943 году.



На основе него появилось первое издание Градштейна-Рыжика.

В 1946-ом году Гарри Бейтман умер, оставив большой архив всякой информации по специальным функциям. В конечном итоге его наработки были опубликованы под названием Bateman Manuscript Project.

Манхэттенский проект, а в дальнейшем и проект разработки водородной бомбы так же служили заказчиками и потребителями специальных функций. В 1951 году, к примеру, Милт Абрамовиц (Milt Abramowitz) из Национального Бюро стандартов работал над таблицами волновых функций Кулона, которые нужны ему были в ядерной физике.



Из этого постепенно выросла книга Абрамовица-Стигана, изданная в 1965 году, которая стала литературой номер один для людей в Америке, пользующихся специальными функциями.



В 60-е и 70-е много внимания стали уделять разработке численных алгоритмов для компьютеров. И вычисление специальных функций было излюбленным местом.

Работа в большинстве случаев была уж больно специфична — огромное количество времени могло тратиться на какую-то конкретную функцию Бесселя конкретного порядка с определённой точностью вычисления. Но постепенно возникали библиотеки с коллекциями определенных алгоритмов по вычислению специальных функций. Однако всё ещё большое количество людей до сих пор пользуется справочниками с таблицами, которые часто можно увидеть на самых видных местах в научных библиотеках.

Специальными функциями я начал заниматься, когда был ещё подростком — в середине 1970-х. Официальная математика, которой я обучался в школе в Англии, сознательно избегала специальных функций. Она заключалась в том, чтобы с помощью каких-нибудь хитрых трюков находить ответ, используя лишь элементарные функции. Мне это не особо нравилось. Мне хотелось чего-то более общего, более практичного. Менее хитроумного. И мне понравилась идея специальных функций. Они казались более эффективным инструментом. Однако их обсуждение в книгах по математической физике никогда не казалось достаточно систематизированным. Да, они были более мощными функциями. Но они всё еще казались несколько условными: что-то вроде зоопарка из любопытных созданий с именами впечатляющего звучания.

Думаю, мне было где-то 16, когда я впервые начал использовать специальные функции для каких-то реальных задач. Это был дилогарифм. Он был в работе по физике частиц. И мне стыдно сказать, что я просто обозначал его как f.



Однако в своё оправдание скажу, что полилогарифмы тогда были не особо-то и изучены. Обычные книжки по математической физике содержали интегралы Бесселя, эллиптические интегралы, ортогональные многочлены и даже гипергеометрические функции. Но никаких полилогарифмов. Как оказалось, ещё Лейбниц писал о них. Но они почему-то не попали в привычный «зоопарк» специальных функций; и единственная реальная информация о них, которую я смог найти в середине 1970-х, была в книге по микроволнам 1959 года издания инженера Леонарда Льюина (Leonard Lewin).

Вскоре после этого мне приходилось часто вычислять интегралы для диаграмм Фейнмана. И тогда я понял, что полилогарифмы — это ключ, это то, что нужно. Полилогарифмы стали моими верными друзьями, и я начал изучать их свойства.



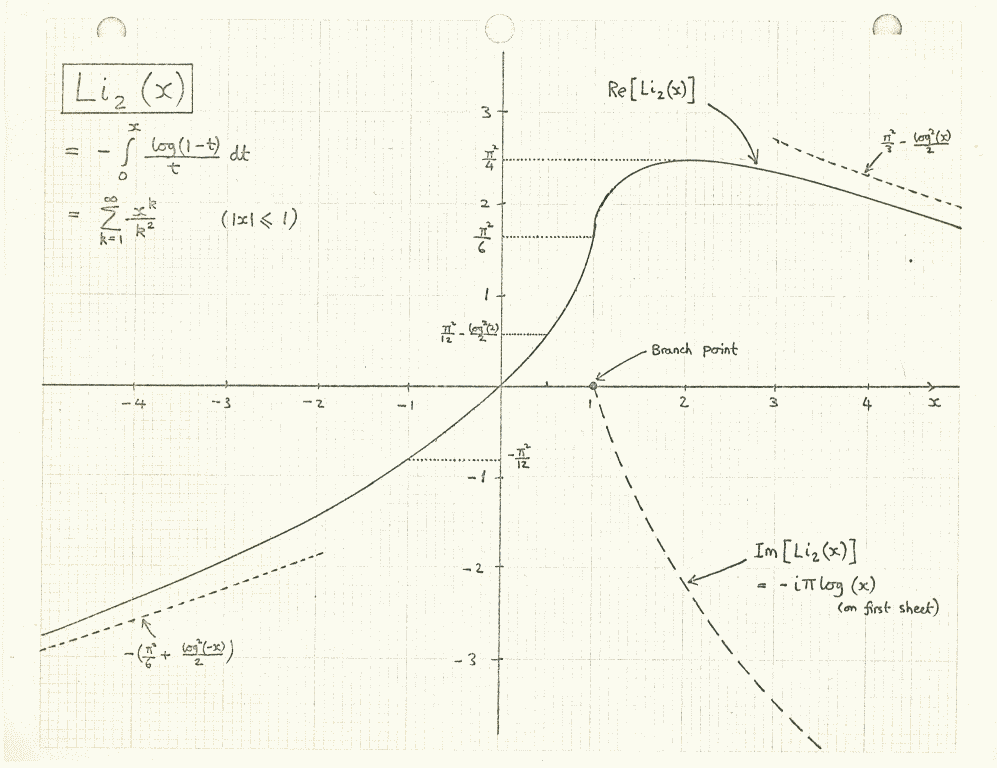
И было кое-что, что я тогда заметил, значение чего я действительно осознал лишь много времени спустя. Мне стоит пояснить, что умение хорошо работать с интегралами в то время было в своём роде визитной карточкой физика-теоретика.

Вообще, я бы никогда не сказал, что у меня есть какие-то таланты в алгебре. Однако каким-то образом я обнаружил, что если использовать некоторые причудливые специальные функции, то можно значительно быстрее и удобнее брать интегралы. Меня даже стали часто просить что-нибудь проинтегрировать. Мне это казалось весьма удивительным. Особенно если учесть, что любой интеграл я просто записывал в виде параметрической производной интеграла от бета-функции.

Это меня навело на мысль, что процесс интегрирования можно сильно облегчить, работая с какими-то более общими функциями, а затем переходя обратно. Примерно как решать кубическое уравнение в комплексном виде и затем переходить к действительным числам. Да и вообще, есть множество других примеров подобного в математике.

Так вот, где-то в 78-ом я понял, что должен писать код и автоматизировать процесс взятия всех этих интегралов. В качестве примера могу привести блок-схему программы на Macsyma, которую я тогда написал.



Комбинация алгоритмов и поиск по таблице. Это и правда работало и было весьма полезным.



Помимо полилогарифмов, я так же занимался и другими специальными функциями. Функциями Бесселя K-типа в космологических расчётах, например.



Вычисления в квантовой хромодинамике ознаменовали расцвет дзета-функции во всей красе. Я разработал теорию "областей событий", которая всё ещё находит приложения в экспериментальной физике. Она была полностью основана на сферических гармониках и многочленах Лежандра.

Мне запомнился день, когда при проработке одной теории из квантовой хромодинамики я натолкнулся на модифицированную функцию Бесселя 1-го типа. Я никогда до этого не встречался с ними.

Знаете, разработка специальных функций часто сопрягалась какими-то интересными событиями. Да и вообще — всегда было здорово работать с задачами, поставленными в терминах специальных функций. Это было довольно эффектно.

Иногда это казалось весьма забавным — показывать какому-нибудь старому физику какую-то математическую задачу. Они смотрели на них как археологи на осколки древних горшков. Если бы у них были бороды, они бы почёсывали их. И, стоит заметить, это мог бы быть и многочлен Лагерра.

И когда кто-то говорил, что его проблема включает какие-то специальные функции, было впечатление, что речь идёт о том, что она приправлена какими-то восточными пряностями. И да, Восток тоже был включён в работу. Потому что как-то, по крайней мере в США в конце 1970-х, казалось, что специальные функции весьма «русские» на вкус.

Как минимум среди физиков книга Абрамовица-Стигана была хорошо известна. А Янке и Эмде были практически неизвестны. Как и Магнус, Оберхеттиннджер и другие. Полагаю, что только математикам и был известен проект рукописей Бейтмэна (даже в Калтехе, где он был основан). Однако в физике русские издания пользовались большой популярностью, особенно Градштейн-Рыжик.

Я никогда до конца не понимал, почему среди специальных функций было такое сильное русское влияние. Говорили, что это потому, что у русских не было хороших компьютеров, и им приходилось делать всё в максимально аналитической форме. Думаю, что это не совсем так. Думаю, что пришло время рассказать историю, которая стоит за Гродштейном-Рыжиком.



Я до сих пор не знаю всей истории, но я расскажу то, что знаю. В 1936-ом Иосиф Моисеевич Рыжик написал книгу под названием Специальные функции, которая была издана Объединённым научно-техническим издательством (ныне Физматлит). Рыжик умер в 1941-ом — то-ли в блокадном Ленинграде, то-ли на фронте. В 43-м справочник формул под авторством Рыжика был опубликован Государственным технико-теоретическим издательством (то же издательство, которое поменяло название). Сама книга формулирует свою цель как решение проблемы с нехваткой справочников с формулами. В ней сказано, что некоторые интегралы, приведённые в этой книге, встречаются впервые, а остальные происходят из трёх книг: французской 1858-го года, немецкой 1894-го и американской 1922-го. Основные усилия были направлены на систематизацию интегралов и некоторого их упрощения за счёт введения новой специальной функции s, которая равна . В ней выражается благодарность трём известным математикам из МГУ. По сути это всё, что мы знаем о Рыжике. Больше, чем о Евклиде, но ненамного.

Что ж, двигаемся дальше. Израиль Соломонович Градштейн родился в 1899 году в Одессе и стал профессором математики в Московском Государственном Университете. Но в 1948 году он был уволен в рамках советского гонения на еврейских учёных. Чтобы заработать, он хотел написать книгу. И решил продолжить дело Рыжика. Вероятно, он никогда не встречался с ним. Но он составил новую редакцию, и в третьем издании книга издавалась под авторством Градштейна-Рыжика.

Градштейн умер по естественным причинам в Москве в 1958 году. Ходила легенда, что одного из тех, кто работал над книгой Градштейна-Рыжика расстреляли в рамках антисемитских гонений из-за ошибки в таблицах, которая повлекла за собой авиакатастрофу.

Тем временем, начиная где-то с 1953 года, Юрий Геронимус, который работал с Градштейном в МГУ, стал помогать ему с редактированием таблиц и добавил некоторые приложения для специальных функций. Затем в работу были включены ещё несколько людей. А когда таблицы были опубликованы на Западе, то появились некоторые вопросы об авторских отчислениях. Геронимус жив-здоров и живёт сейчас в Иерусалиме — Олег Маричев звонил ему на прошлой неделе.

Я думаю, что интегралы — это что-то вечное. Они не несут следы своих создателей. Итак, у нас есть таблицы, однако в действительности мы не совсем понимаем, откуда они появились.

Что ж, таким образом, в конце 1970-х я стал довольно серьёзно увлекаться специальными функциями. Итак, в 1979 году, когда я начал создавать SMP — своего рода предшественника Mathematica, требовалось добавить мощную поддержку специальных функций. Это казалось очевидным —перепоручить математическую рутину компьютеру.

Вот один из самых ранних концептов SMP, написанный в первые несколько недель проекта. Тут уже имеют место быть специальные функции.



Вот немного более поздний.



Первая версия SMP была выпущена в 1981-ом году и уже работала с практически всеми основными специальными функциями.



Некоторые из них были слабо проработаны. Однако многие были довольны тем, что они могут работать в этой среде со своими функциями. Численная работа с функциями была организована довольно примитивно. Но одна вещь, которая сыграла весьма положительную роль, заключалась в том, что мы серьёзно поработали над вычислением довольно общих гипергеометрических функций. И затем мы рассмотрели множество других функций как их частные случаи. И всё было в порядке. Да, кроме одного факта — наиболее интересные области функций часто оказывались вырожденными. Так что на практике даже числовые значения получались лишь в некоторых областях.

Ну, прошло несколько лет. И в 1986 году я начал создавать Mathematica. И на этот раз я хотел всё сделать как надо — числовые значения для всех функций, всех значений параметров, во всей комплексной плоскости, с любой точностью.

Сначала я подумал, что я, возможно, должен поговорить с экспертами. И я очень отчётливо помню телефонный звонок, который у меня состоялся с кем-то из государственной лаборатории. Я объяснил, что я хочу сделать. И воцарилась тишина. И потом мне ответили: "Послушайте, Вам следует понять, что к концу 90-х мы надеемся учетверить точность получения значений функций Бесселя целочисленного порядка".

Что ж, нам нужен другой подход. Проблема заключалась в том, что тот парень с функциями Бесселя из лаборатории считал, что один лишь он будет заниматься численными методами. Однако я понимал, что для этих задач нам нужна автоматизация. А затем Джерри Кейпер разработал автоматизированную систему для поиска алгоритмов для вычисления функций. Получилось нечто в стиле A New Kind of Science — были заданы общие формы рациональных приближений к функциям. Затем последовала масштабная работа по оптимизации параметров.

И это подействовало, причём весьма хорошо. И все функции стали иметь хорошие числовые значения.

Знаете, вообще, стоит проделать большую работу, чтобы добавить специальную функцию в Mathematica. Вам не просто нужно заниматься численными значениями — для всех значений параметров и прочего. Так же нужно реализовать все их свойства в символьном виде. То есть производные, ряды, асимптотические разложения. Со связью с аргументами и параметрами. И ещё куча всего. Часто нам приходится выводить совершенно новые формулы, которые никогда не встречались в литературе.

И, конечно же, мы должны завязать функции с интегралами, дифференциальными уравнениями, сумами, интегральными преобразованиями. Плюс FunctionExpand и FullSimplify и ещё очень много всего. Получается длинный список.

Зачастую самые сложные моменты возникают в точках ветвления функций. Большинство непрерывных специальных функций определяются неявно, как правило из дифференциальных уравнений. То есть функция, как в случае с квадратным уравнением, к примеру, может иметь несколько значений, которые соответствуют разным областям её римановой поверхности.

Чтобы выбрать верную функцию, необходимо выбрать некоторую основную область. Тем самым зашить разрывы и убрать ветвления, так сказать. А представление этих разрывов и ветвлений в символьном виде — очень непростое занятие. Даже для элементарных функций. Вот, к примеру, избавленная от ветвлений версия формулы .



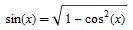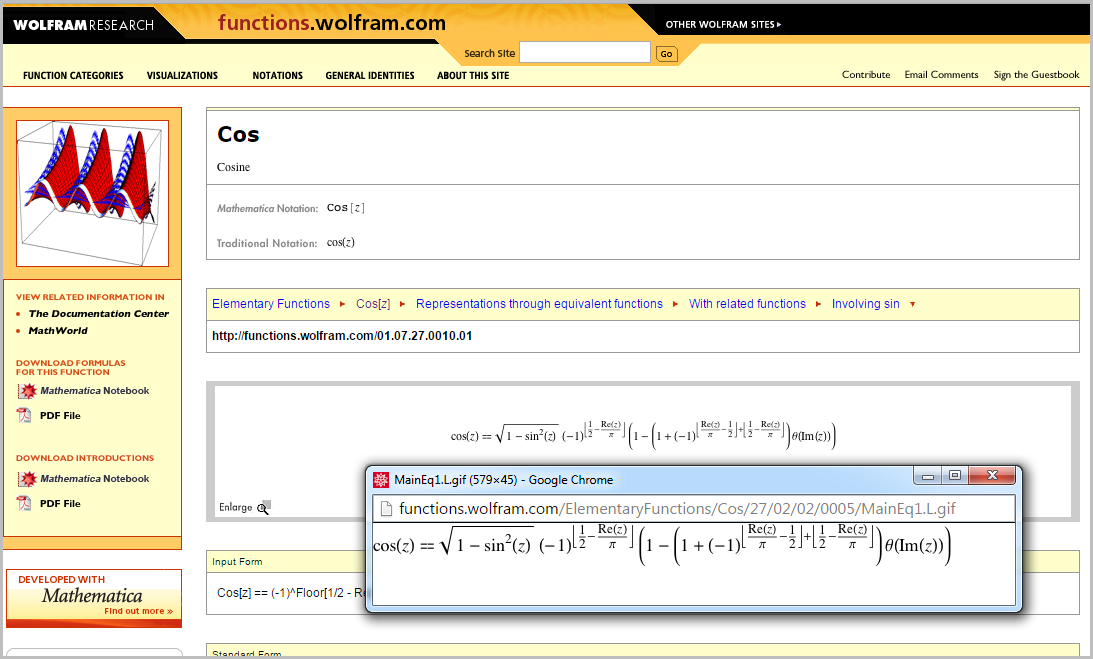
Этому не учат в школе. И, фактически, мы вывели её довольно недавно. Однако для того, чтобы символьные манипуляции в комплексной области были корректными, нужно пользоваться именно ею.

Что ж, мы проделали большую работу в сфере специальных функций в Mathematica. С алгоритмами. Формулами. И вот, наш сайт Wolfram Functions Site. Огромное количество человеко-часов и всяческих продуманных автоматизаций были помножены на все те знания о специальных функциях, что имеются в мире.

Думаю, у нас получилось. Трудно получить какую-то количественную оценку, однако то, что с этими функциями теперь столь же просто работать, как с синусом и косинусом, сделало их, на мой взгляд, значительно более популярными. Они перестали быть какой-то диковинкой, о которой мало кто слышал. Теперь их кто угодно может получить с помощью онлайн-интегратора (на данный момент сервис устарел и его функционал полностью покрывается Wolfram|Alpha, прим. ред.). Они больше не подобны каким-то рудиментам математики. Они созданы быть простыми и полезными.

Что ж, я обещал рассказать о будущем специальных функций. Интересно проследить некоторые тенденции. Есть множество специальных функций, которые всегда в моде. Как Бесселевы или ортогональные многочлены. А есть, к примеру, полилогарифмы, которые находились в тени длительное время, однако обрели популярность в некоторых отдельных приложениях. А есть и специальные функции, которые до сих пор мало кому известны. Как трансцендентные функции Пенлеве. Им уже больше сотни лет. О них люди иногда спрашивают в Mathematica.

Ну, в разработке Mathematica, мы часто поднимаем вопрос о будущем специальных функций. Какие функции и в каких направлениях окажутся полезными и востребованными? На проработку некоторых из них будет затрачено большое количество усилий, однако их судьба будет такая же, как и у гудерманиана.

Однако одна тенденция, в которой не обошлось без участия Mathematica, очевидна — получать новые функции из дискретных разностных уравнений точно так же, как и из непрерывных дифференциальных уравнений. То есть с помощью RSolve и Sum вместо DSolve и Integrate. Конечно, как и со многими другими идеями, в этом нет ничего принципиально нового. Джордж Буль в 1859-ом и в 1860-ом году соответственно опубликовал работы — по дифференциальным уравнениям и по конечным разностям: A Treatise on Differential Equations и A Treatise on the Calculus of Finite Differences. Для пятой версии Mathematica мы подняли результаты его работ и алгоритмизировали их.

Что ж, с точки зрения Буля и Бэббиджа, ответ не будет считаться решением, если он представлен не в виде комбинации элементарных функций. Но мы спокойно можем использовать дискретные специальные функции. И я не удивлюсь, что если мы их правильно зададим, то обнаружим, что они уже рассматривались в 17-ом веке.

Размышления обо всём этом наводят на мысли о некой более общей теории специальных функций. Нечто вроде нового фундамента, новых основ.

Качественная картина: ещё со времён Вавилона специальные функции были своего рода центрами притяжения в математических вычислениях. В бесконечном море возможных функций они являются якорными точками. Функции с несколькими аргументами, которые могут быть использованы как примитивы в различных вычислениях.

Тут прослеживается аналогия со встроенными функциями в Wolfram Language (Mathematica). Есть всё то пространство возможных вычислений, которые бы люди хотели осуществлять. И наша работа в проектировании Mathematica заключается в том, чтобы задать наиболее удачные примитивы, из которых будут состоять вычисления.

Так чем специальные функции так хороши? Подойдём к этому вопросу с практической точки зрения. Какими специальными функциями мы чаще всего пользуемся? Пожалуй, как Mathematica, так и сайт Wolfram Functions лучше всех смогут ответить на этот вопрос.

Вот несколько фактов. Во-первых, большинство специальных функций содержат небольшое количество аргументов. Чаще всего — два. В старых таблицах в основном приводились функции с одним аргументом и лишь иногда с двумя. Потому они были весьма неудобными.

Конечно, сейчас у нас уже нет тех ограничений, что действовали тогда. Но по мере роста количества аргументов у функции растёт количество особых областей, разрывов и прочего. Трудно всё это отследить, а зачастую теряется целостность того, что некогда было определённой специальной функцией.

Можно задаться другим вопросом: как и с чем может быть связана какая-то конкретная специальная функция? Через какие соотношения её можно выразить? Как её можно связать с другими функциями или с самой собой? Что ж, на этот вопрос можно ответить даже количественно с Wolfram Functions Site. Вот полная матрица того, какие функции с какими имеют связи, представленные на Wolfram Functions Site.



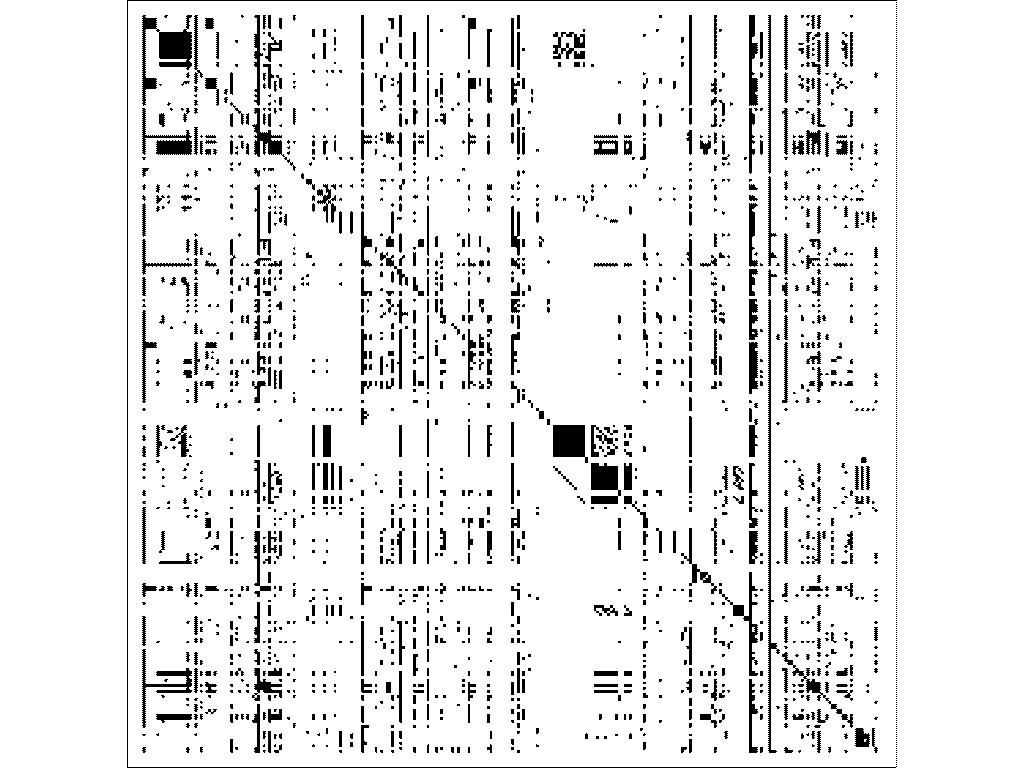
А вот таблица наиболее связанных функций, представленная в Google-pagerank-стиле.



А вот граф, отображающий четыре наиболее популярных ссылки от каждой функции.



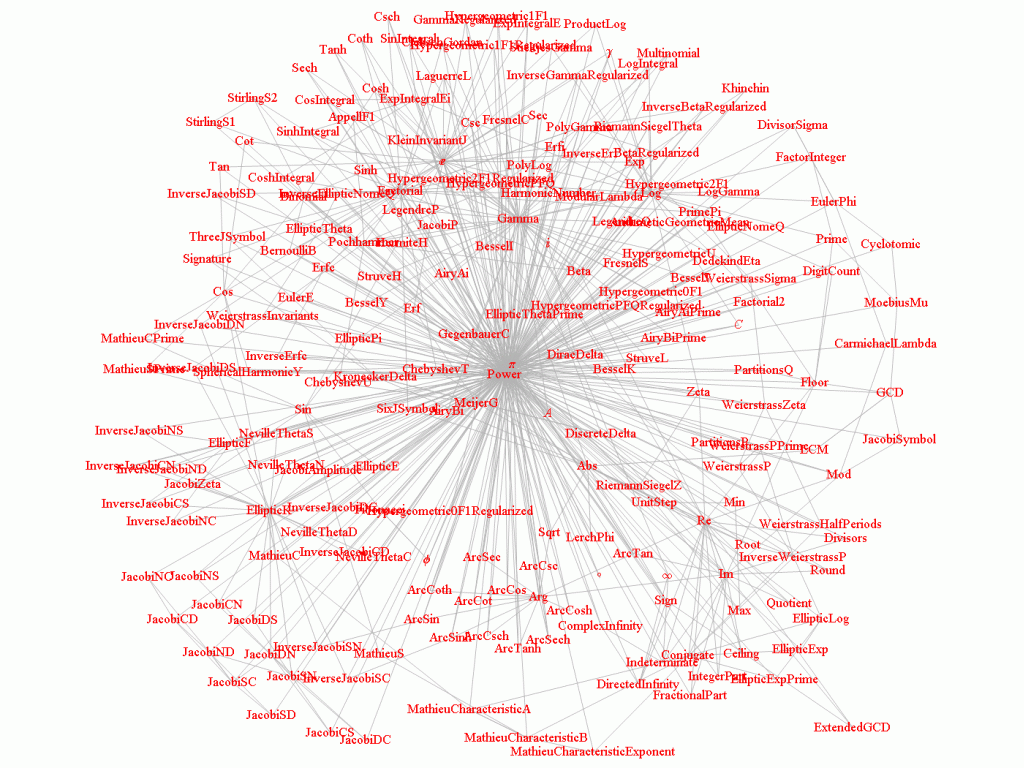
Можно было бы думать, что чем больше отношений функция имеет, то тем она полезнее. Однако Гамма функция, которая является одной из самых широко используемых, имеет не так уж и много связей с другими функциями. Тогда как функция Вейештрасса, о которой нельзя сказать подобное, имеет гораздо больше связей. А Дзета-функция вообще стоит особняком.

Итак, давайте теперь рассмотрим более тщательно непрерывные специальные функции, которые мы обычно используем. С самого начала использования исчисления степенные ряды являлись одним из основных способов, с помощью которого можно рассматривать функции. И, действительно, по существу, все специальные функции, которые мы используем, имеют одну важную особенность в своём степенном ряду — все коэффициенты рациональны. Так что коэффициент перед 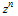является некоторой рациональной функцией от n. И это означает, что функции являются гипергеометрическими. Они могут быть представлены через 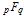— обобщённые гипергеометрические функции.

И в некоторой степени значения p и q для какой-то конкретной функции коррелируют с тем, насколько экзотична эта функция. Степень (Power) числа соответствует {0,0}. Тригонометрическим и обратным тригонометрическим — {1,0}. Функции ошибок (Erf) — {1,1}. BesselJ — {0,1}. EllipticK — {2,1}. А 6-j символу — {4,3}. Но некоторые функции, которые мы используем, не являются гипергеометрическими. Подобно функциям Матье, например.

Может быть, это и есть ответ: по каким-то причинам те функции, которые мы наиболее часто используем, имеют рациональные степени в степенном разложении, а специальные функции — это способ всё это структурировать. Однако есть простой способ показать, что на самом деле всё не так просто.

Можно просто перечислить все возможные ряды с рациональными степенями и задаться вопросом — каким функциям они соответствуют. Это легко сделать с Sum в Mathematica. Вот некоторые результаты:



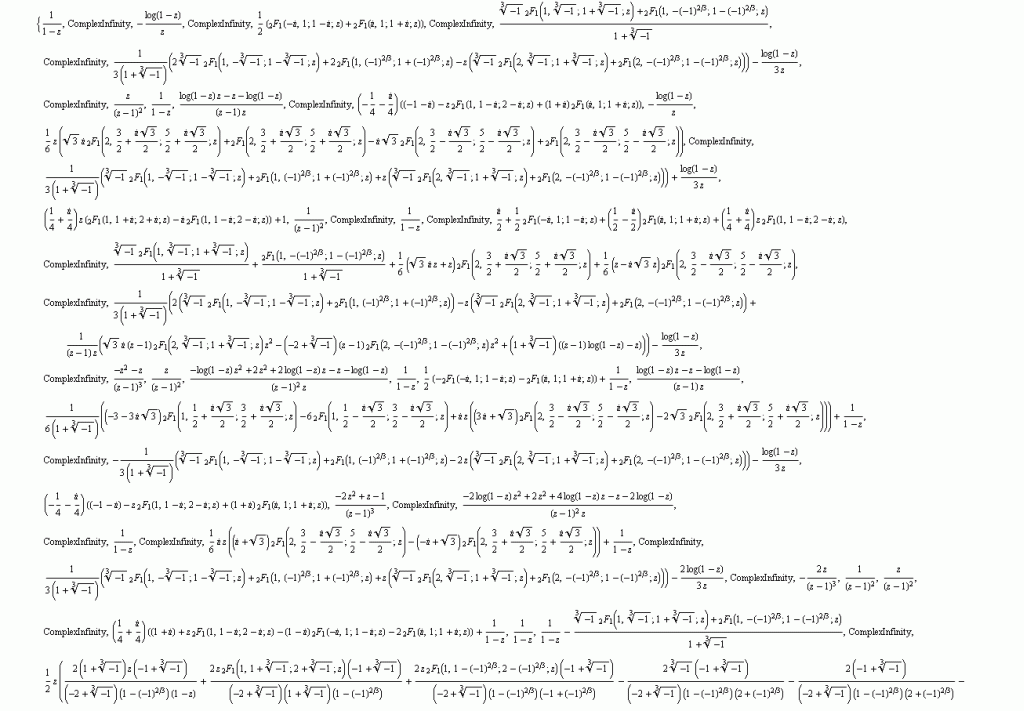
Безусловно, всё есть некоторая комбинация гипергеомерических функций 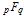. Но что примечательно — насколько близки гамма-функция и группа функций Бесселя. Это практически чистые .

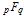Получается, есть некоторый другой процесс отбора, выдающий стандартные специальные функции.

Ещё одна важная характеристика гипергеометрической функции состоит в том, что она может быть задана в дифференциальной форме. Но вот другая мысль: возможно, специальные функции являются решением определённого класса дифференциальных уравнений.

И это, безусловно, гораздо ближе. Давайте просто представим, что мы, скажем, перечисляем дифференциальные уравнения второго порядка, строя целочисленные полиномы из последовательностей стоящих друг за другом целых чисел. Потом применим DSolve. И вот результат.



Довольно интересно получается. Лишь из одного этого класса дифференциальных уравнений мы получили так много популярных специальных функций. В каком-то смысле это часть ответа.

Однако это опять-таки лишь часть ответа. Посмотрите на весь массив результатов DSolve. Есть пустоты. Дыры — недостатки DSolve? Нет, далеко не всегда так. Часто это свидетельствует о наличие еще каких-то специальных функций, неизвестных нам.

Нет ничего сложного в том, чтобы задать уравнения, из которых они получаются. Даже с помощью интегралов. Как, например, интеграл от Sin[Sin[x]]. Можно было бы предположить, что это будет довольно простая специальная функция. Как и многие другие интегралы от вложенных тригонометрических функций. Однако нет. Чтобы выразить его через специальные функции, Вам потребуется гораздо более сложные гипергеометрические функции от двух переменных.

Довольно забавно получается. Integrate в Mathematica достаточно хороша, чтобы справиться с этим. Просто попробуйте разные интегралы, и Вы увидите, где границы ее возможностей при работе со специальными функциями.

И вот довольно-таки фундаментальный вопрос: какие виды вычислений следует ожидать, чтобы дать точные решения в терминах специальных функций? В теоретической физике можно заметить такое негласное соглашение, что то, что может называться физической задачей, должно требовать серьёзных усилий для решения. Квантовая хромодинамика. Турбулентность в жидкостях. Да что угодно. И выдавать формулы, которые будут объяснять, что происходит в системе.

И в том смысле это имеет решающее значение для самоидентификации теоретической физики. То есть всё это должно пораждать предсказательные теории. Я имею в виду, что чтобы выяснить, что происходит в задаче двух тел для идеальной планеты, вращающейся вокруг звезды, кому-то бы пришлось проследить каждое положение планеты. Но теоретическая физика гордо говорит ему, что этого не нужно делать. Она просто предлагает воспользоваться одной формулой для получения результата. Тем самым задача предсказания к сводится вычислению формулы.

Так каковы границы этого подхода? Является ли просто вопросом времени то, когда появятся формулы для всего на свете?

В рамках традиционных физики или математики эти вопросы не поднимаются. Но новый вид науки, который я так долго разрабатывал, содержит ответ на этот вопрос.

Стоит помнить, что один из его фундаментальных принципов — охват всех возможных простых программ со всеми возможными системами правил. Традиционные точные науки сильно ориентированы на математику. Разговоры ведутся только о тех вещах, которые могут быть сформулированы с терминологии традиционных математических конструкций. Однако теперь — с новым видом науки — мы можем охватить гораздо больше. Мы можем исследовать всю вычислительную вселенную со всеми возможными типами основных правил.

И что мы там сможем найти? Хорошим примером является моя любимая коллекция одномерных клеточных автоматов. Вот они, всё их множество.



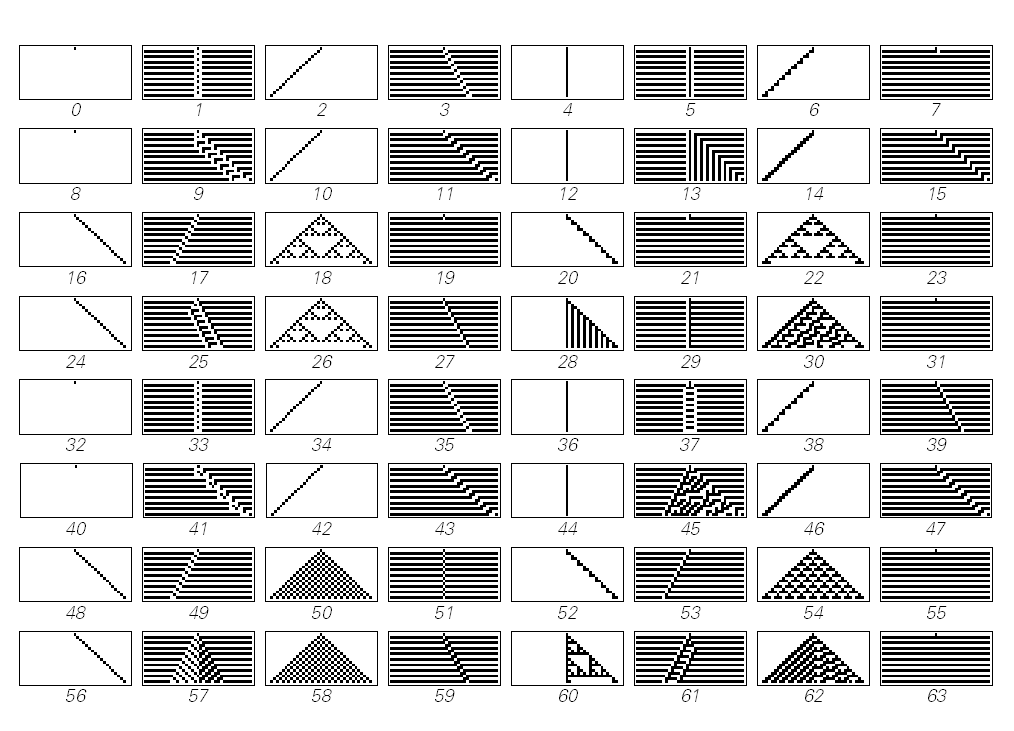
Многие делают довольно простые вещи. И выдают одни и те же структуры. Или, по крайней мере, повторяющиеся.

Попробуем представить, что мы можем найти формулу, чтобы это осуществить. С помощью этого можно понять, к примеру, какой цвет у некоторой клетки будет на некотором шаге.

Но что насчёт этого парня? Моего любимого 30-го правила?



Есть ли формула для того, чтобы определить, что происходит после некоторого количества итераций?

Или для этого?



Не думаю.

Думаю, на самом деле подобные системы по своей сути являются вычислительно неприводимыми.

Мы можем рассматривать такую систему, как 30-е правило, как некоторый процесс вычисления. Если мы попытаемся предсказать, какой результат она нам выдаст, то нам так же потребуется выполнить какие-то вычисления. И в некотором роде успехи таких традиционных областей, как теоретическая физика, на самом деле были основаны на решении каких-то гораздо более сложных систем, чем те, которые мы изучаем. Так что нам нужно дать какое-то определение тому, что система будет делать, если у неё будет гораздо меньше вычислительных возможностей, чем ей требуется.

Да, одна из основных идей в моей книге — то, что я называю "Принципом вычислительной эквивалентности". Этот принцип утверждает, что практически все системы, поведение которых не является очевидно простым, в точности эквивалентны их вычислительной сложности. Даже несмотря на то, что как наш мозг, так и наши математические алгоритмы могут работать с весьма сложными правилами, они не могут проводить вычисления, которые хоть сколь-нибудь более сложные, чем, к примеру, то, что делает 30-е правило. То-есть это значит, что поведение 30-го правила является вычислительно неприводимым: мы не можем объяснить, как себя будет вести система с помощью какого-то процесса, который является более эффективным, нежели простое воспроизведение 30-го правила.

Таким образом мы никогда не сможем получить какое-то точное решение для 30-го правила — скажем, формулу, аргументами которой будут являться координата клетки и шаг, а выход функции — цвет клетки.

Кстати, доказать это можно, если доказать вычислительную универсальность 30-го правила, то есть что с его помощью можно проводить любые вычисления, эмулировать любую систему. И это —способ понять, почему это правило не может иметь точного решения. В некотором роде потому, что это решение должно быть любым возможным вычислением. Что означает, что оно не может быть какой-то небольшой формулой.

Хорошо, что из этого следует в отношении специальных функций? Ну, если мы столкнёмся с большими объемами вычислительной неприводимости, то специальные функции нам особо не помогут. Потому что для многих проблем просто не будет возможности составить какую-то формулу — неважно, со специальными функциями или с чем бы то ни было.

Одна из главных идей моей книги заключается в том, что в вычислительном мире всевозможных программ проблема вычислительной неприводимости решается очень просто. А причина, по которой мы редко с ней сталкиваемся состоит в том, что такие области знаний, как теоретическая физика, специально избегают вычислительной неприводимости.

Однако в природе, особенно в таких областях, как биология, можно столкнуться с гораздо более широкой выборкой представителей вычислительной вселенной. То-есть там часто можно встретить вычислительную неприводимость. Теоретические науки не смогли особо продвинуться в этой сфере.

Хорошо, давайте теперь взглянем на систему наподобие 30-го правила, или, скажем, на небольшое уравнение в частных производных, которое я нашёл, исследуя пространство всех возможных подобных уравнений.



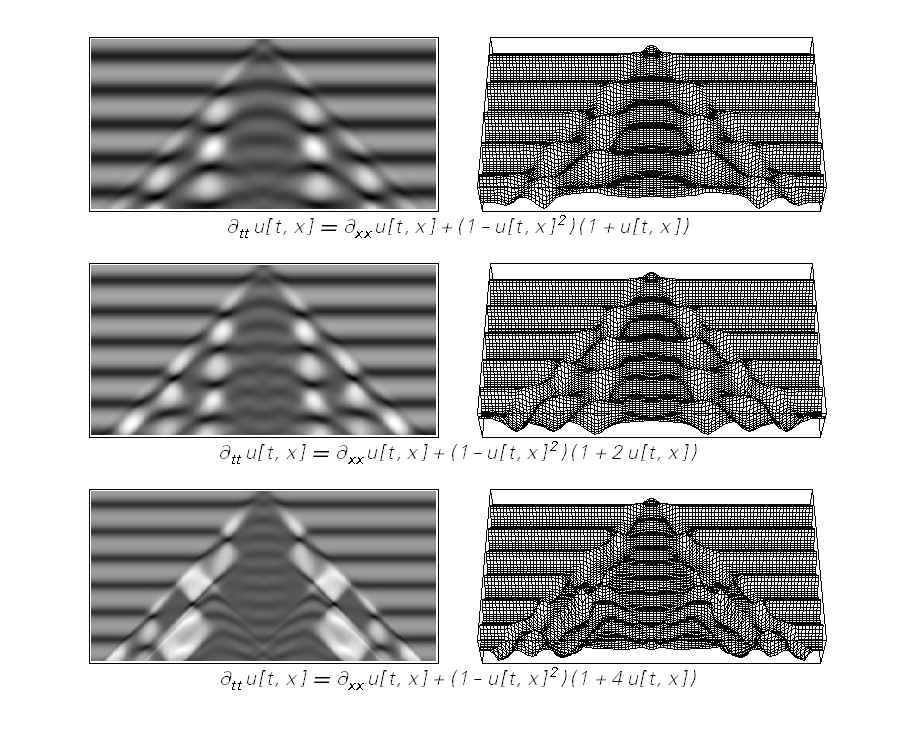
Так почему бы не существовать какой-нибудь высокоуровневой специальной функции, которая отражала бы, что происходит в этих системах?

Конечно, мы могли бы просто задать специальную функцию для 30-го правила. Или специальную функцию для этого УРЧП. Но это своего рода обман. И путь по которому мы идем, дает нам понять, что специальная функция будет чересчур «специальной». Конечно, чисто номинально это ускорило бы использование 30-го правила или этого УРЧП. Но на этом — всё. Она не будет подобно функции Бесселя всплывать в мириадах различных задач. Она будет служить лишь для решения конкретно этой задачи.

Попробуем обобщить вышесказанное. Дело в том что когда есть некоторая область вычислительной неприводимости, существует и множество отдельных областей, где её можно избежать. Смысл специальной функции, которая не будет бесполезной, заключается в том, что множество различных проблем должны легко сводиться к этой специальной функции.

Получается, что сфера всех задач, в которых не имеется вычислительный неприводимости, включает в себя стандартные специальные функции гипергеометрического вида. А что за пределами этой сферы? Думаю, там полно вычислительной неприводимости. И полно разрозненности. Так что не может появиться никакая новая волшебная специальная функция, которая тут же покроет множество проблемных областей. Это немного напоминает ситуацию с солитонами и подобными вещами. Они хороши в своей области, однако уж очень специфичны. Они обитают в какой-то очень узкой области пространства всевозможных задач.

Хорошо, так как более общо сформулировать эти понятия?

Можно подумать об аналогах специальных функций для множества разнообразных систем. Есть-ли какое-то ограниченное множество специальных объектов, которые пусть и потребуют каких-то вычислений, но с помощью которых можно будет получить какие-то другие полезные объекты?

Можно подумать о числах. Числа могут быть «элементарными», рациональными, алгебраическими. Но что тогда такое — полезные «специальные» числа? Конечно же, это Pi, E, и EulerGamma. Что насчёт других констант? Остальные константы меркнут в тени своих более известных собратьев. Пожалуй, на сайте Wolfram Functions не так уж и много примеров, когда есть какая-то константа, которая периодически всплывает, но для которой нет имени.

[Запись выступления заканчивается на этом месте]

---

В 10-й версии Wolfram Language (Mathematica) встроены сотни специальных функций.

Подробнее о них вы можете узнать здесь:

• Списки (по группам) специальных функций, реализованных в Wolfram Language (Mathematica)
• Cтатья документации о специальных функциях в Wolfram Language