
Перевод поста Ed Pegg Jr."Biggest Little Polyhedron—New Solutions in Combinatorial Geometry".
Скачать файл, содержащий текст статьи, интерактивные модели многогранников и код, приведенный в статье, можно здесь.
Выражаю огромную благодарность Кириллу Гузенко за помощь в переводе.
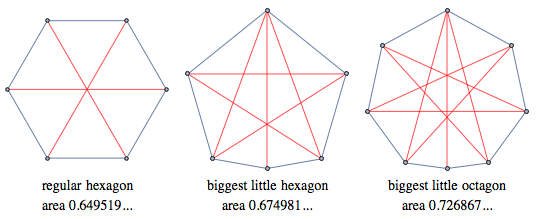
Во многих областях математики ответом будет единица 1. Возведение неотрицательного числа в квадрат, которое больше или меньше единицы, даст большее или меньшее число соответственно. Иногда для того, чтобы определить, является ли что-то «большим», необходимо выяснить, больше ли единицы наибольший размер этого объекта. К примеру, гигантский гексагон Сатурна с длиной стороны в 13,800 км можно было-бы отнести к большим. «Малый многоугольник» — это тот, у которого максимальное расстояние между вершинами равно единице. В 1975 году Рон Грэм открыл наибольший малый шестиугольник, который, как показано ниже, имеет большую площадь, чем у правильного шестиугольника. Красные диагонали имеют единичную длину. Все остальные (непроведённые) диагонали имеют меньшую длину.
Мне всегда было интересно, как будет выглядеть самый большой малый многогранник. В Mathematica 10 был представлен новый функциональный объект Volume[ConvexHullMesh[points]], и я подумал, что можно было бы решить эту задачу, выбирая случайные точки. Ниже представлен код для выбора, вычисления и визуализации случайного малого многогранника. Тысячи раз прокрутив этот код, можно будет получить неплохое приближение в лучшем из результатов. Вот, тут я три раза запускал код. Один из результатов, вероятно, лучше остальных.

Ниже на изображении приведены наилучшие решения, которые были получены через случайно выбранные точки. Я выложил это в Wolfram Community в обсуждении наибольший малый многогранник (далее – НММ) и получил несколько полезных комментариев от Робина Хьюстона и Тодда Роланда. Для поиска решений я решил использовать результаты "визуализации задачи Томпсона". В задаче Томсона электроны отталкиваются друг от друга на сфере. 12 отталкивающихся друг от друга точек стремятся к вершинам икосаэдра, что не эффективно для НММ, так как наибольшие расстояния проходят через центр сферы, так же как и для правильных шестиугольников в двумерном случае. Я изменил код для задачи Томпсона так, что точки отскакивали друг друга и ото всех противолежащих, и это дало неплохие начальные значения.

Для четырёх точек решением будет правильный тетраэдр с объёмом
Для пяти точек решением будет равносторонний треугольник с единичными длинами сторон и единичный перпендикуляр к этому треугольнику, а объём получится равным

Я буду использовать термин 6-НММ для обозначения наибольшего малого многогранника с шестью точками. В 2003-ем году объём 6-НММ был вычислен с точностью до четырёх знаков [2,3]. Ниже представлены 6-НММ и 7-НММ, единичные диагонали выделены красным.

Для того чтобы найти их самостоятельно, сперва я выбрал наилучшие варианты из более чем тысячи, а затем использовал алгоритм имитации отжига (simulated annealing) (вероятностная задача поиска хорошего приближения к глобальному оптимуму данной функции в широком пространстве поиска – прим. пер.) для улучшения результатов. Для каждой из точек оптимальных решений я перебирал пространство вокруг этих точек для поиска лучшего решения, ненамного их смещая. Затем я ещё более уменьшал пространство поиска, и так из раза в раз. Некоторые из решений, казалось, стремятся к взаимной симметричности. К примеру, для семи точек лучшее решение стремилось к этому многограннику со значением r около половины, который представляет относительный размер верхнего треугольника ?456.
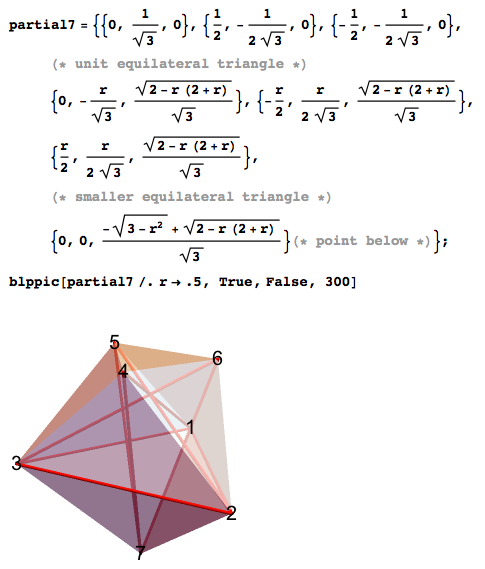
Точный объём можно получить через тетраэдр, который определяется через точки {{2,3,4,7}, {2,4,6,7}, {5,4,7,6}}, а объём первых двух следует утроить из соображений симметрии. Посмотрите на объёмы тетраэдров, и замените любую пару чисел в тетраэдре так, чтобы получился отрицательный объём.

После того, как мы изменили соотношение в последнем тетраэдре, мы можем вычислить точное значение r, которое даст точный и оптимальный объём. Этим же методом воспользуемся и для других случаев.

Решение для 16-НММ занимает более минуты, так что мне пришлось разбить его.

Первое значение в решениях — оптимальный объём, является объектом Root, а второе является оптимальным значением r. Вот, эта таблица будет поаккуратнее.

И это далеко за пределами того, что я смог бы сделать вручную. С помощью случайной выборки точек, алгоритма симуляции отжига, поиска симметрии, Solve[] и Maximize[] мне удалось найти точные значения объёмов n-НММ (наибольших малых многогранников) для n = 6, 7, 8, 9 и 16.
Вид 8-НММ с нескольких сторон, где красным выделены единичные диагонали.
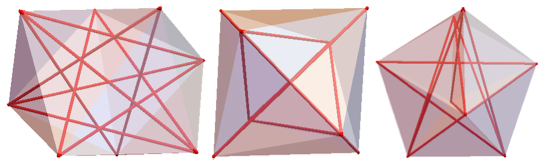
Вид 9-НММ с нескольких сторон:

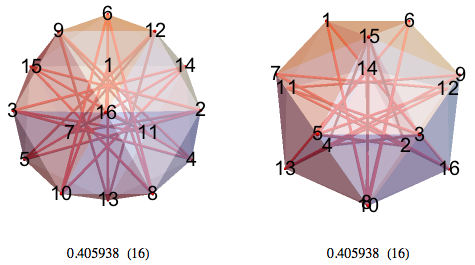
Вид 16-НММ с нескольких сторон:
Указанный ниже 8-НММ содержит единичные перпендикуляры 1-2 и 3-4 над и под основанием соответственно. Представленный ниже 9-НММ содержит треугольники ?123, ?456 и ?789.

Приведённый ниже 16-НММ представляет собой усечённый тетраэдр, состоящий из точек 1-12 с дополнительными точками 13-16.
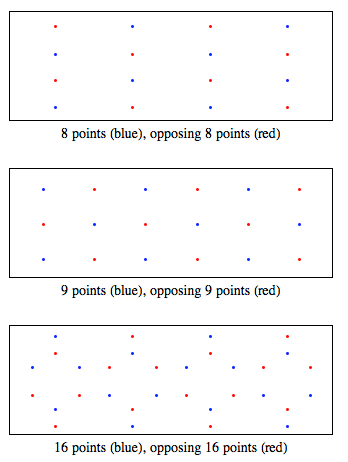
Довольно сложно, не так ли? С помощью метода выбора точек на сфере, случайными числами в промежутках [–Pi; Pi] и [–1; 1] на единичной сфере можно задать равномерное распределение точек. Точки на единичной сфере могут быть отображены обратно в точки в прямоугольнике [–Pi; Pi]x[–1; 1]. Вот, что произойдёт для решений 8,9,16-НММ.
Для 10-НММ мне не удалось найти точное решение, однако я могу представить численное решение с любой степенью точности. Свяжитесь со мной, если у Вас есть догадки, как тут найти root object. В исполняемой версии этой статьи на Wolfram Language в разделе инициализации можно найти это весьма нелёгкое выражение.

Тут представлены два вида 10-НММ с двух разных точек обзора.

Численное решение для 11-НММ можно найти схожим образом.

Вид 11-НММ с двух сторон:

Действительно ли я получил верные решения? Может быть и нет. Для этих симметрий я уверен, что я нашёл локальный максимум. Например, вот функция с локальным максимумом 5 при значении 1.
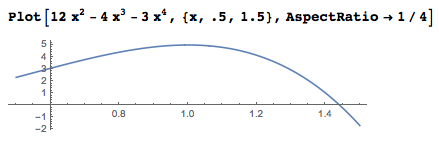
А если заглянуть в графике чуть дальше, то можно будет найти глобальный максимум 32 при значении в -2.

В схожей задаче Томпсона имеется доказательство для 12 вершин икосаэдра, находясь в которых система из 12 электронов находится в потенциальном минимуме. Но для 7, 8, 9, 10, 11 и 13+ электронов задача считается нерешённой. В гипотезе Кеплера предполагается, что гексагональная плотная упаковка есть плотнейшая упаковка для сфер, однако строгое доказательство было получено Томасом Хейлзом лишь 10-го августа 2014-го года. Плотнейшая упаковка для правильных тетраэдров — с отношением 4000/4671 = 0.856347… — была открыта лишь 27-го июля 2010-го года, однако до сих пор не имеет строгого доказательства. Любые заявления о найденном решении следует воспринимать с определённой долей скептицизма; геометрические задачи максимизации, как известно, очень сложны.
Несколько месяцев моё лучшее решение для 11 точек было в локальном максимуме, соответствующем асимметричному НММ. Некоторые (или большинство) из этих решений, скорее всего, локальные, а не глобальные, но какие из них? С этой оговоркой можно посмотреть на самые известные решения для 12-ти и более точек.
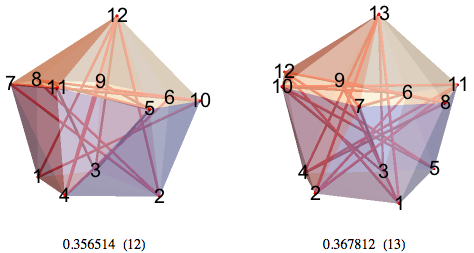
12-НММ имеет вершину в точке 12 и содержит в себе неправильный семиугольник 11-6-7-10-8-5-9 и четырёхугольник 1-4-3-2.
13-НММ имеет вершину в точке 13 и содержит в себе неправильный семиугольник 12-8-10-6-7-9-11 и такой же пятиугольник 1-2-3-4-5.
Мои попытки добавить симметрию привели к фигурам с меньшим объёмом.
По идее, решения для 14-НММ должны быть весьма симметричны, однако они у меня пока-что не получились. Я потратил некоторое время на оптимизацию системы вершина-пятиугольник-пятиугольник для 15-НММ, однако методом случайных точек было получено лучшее решение, в котором симметрия была принесена в жертву объёму.
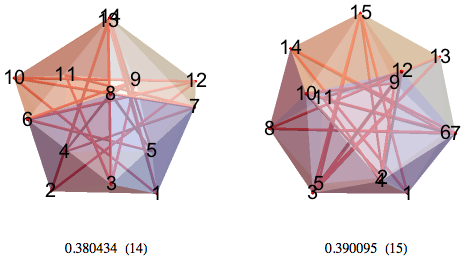
17-НММ, 18-НММ — я надеюсь, что в первом всё в порядке с симметрией.
Что касается 19-НММ и 20-НММ, то 20-НММ — не додекаэдр, так как единичные линии из центра — не лучший вариант.

Как «курносый куб» (snub cube), так и половина огромного ромбокубоктаэдра — все имеют меньший объём, чем 24-НММ.
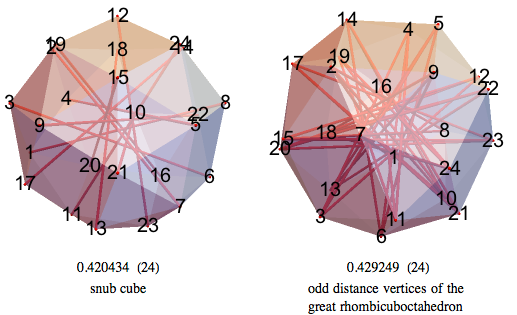
21-НММ и 22-НММ содержат множество семи- и девятиконечных звёзд.
23-НММ, 24-НММ — мой лучший 24-НММ имеет тетраэдрическую симметрию.
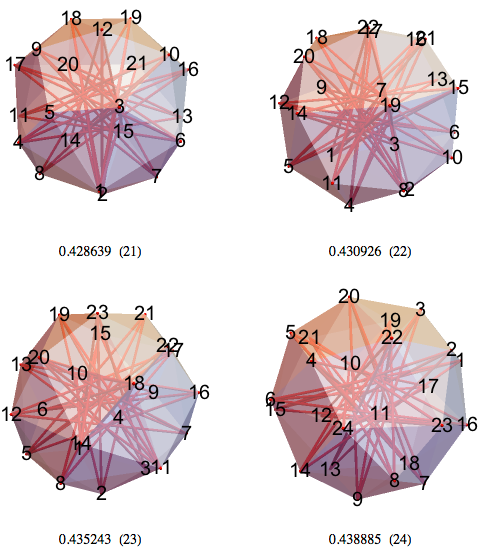
Вот некоторые симметрии в текущем лучшем 24-НММ. Отрезки 1-12 и 13-24 имеют соответствующие длины 0.512593 и 0.515168.
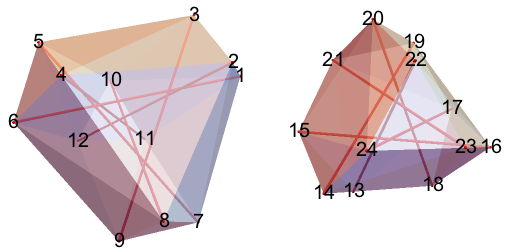
В 16-НММ и 17-НММ единичные отрезки определяют многоугольники. 16-НММ содержит множество семиконечных звёзд.

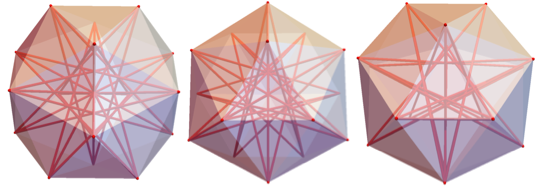
Ниже представлены те же самые многогранники, представленные как сплошные тела, посредством ConvexHullMesh[], для НММ 9-10-11-12, 13-14-15-16, 17-18-19-20, 21-22-23-24, соответственно.

Здесь представлена таблица наилучших известных на данный момент значений.

Вот лучшие решения, которые я нашёл на данный момент, для 4-24 точек.
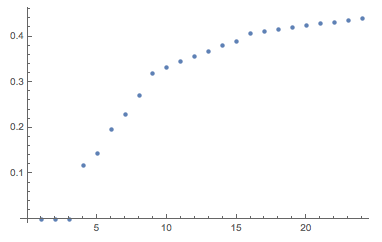
Пусть точки будут расположены так, чтобы максимальное расстояние от начала координат было как можно меньше. Распределение, представленное ниже, указывает на расстояния от начала координат до вершин каждого многогранника, в каждом из которых от 8 до 24 вершин.
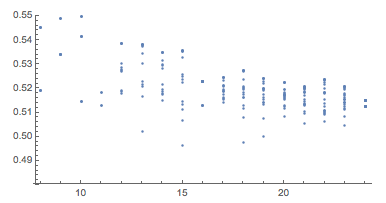
С помощью Mathematica 10.1 удалось получить точные значения для 6,7,8,9-НММ и 16-НММ. Так же с её помощью были найдены очень точные, но численные значения для 10-НММ и 11-НММ и удалось серьёзно продвинуться с 24-НММ. Таким образом, мы получили решения семи ранее нерешённых задач в комбинаторной геометрии — все, благодаря комбинации Volume[ConvexHullMesh[points]]. А какие нововведения в Mathematica 10 помогли лично Вам?
Список литературы
[1] B. Kind and P. Kleinschmidt, “On the Maximal Volume of Convex Bodies with Few Vertices,” Journal of Combinatorial Theory, Series A, 21(1) 1976 pp. 124-128.
doi:10.1016/0097-3165(76)90056-X
[2] A. Klein and M. Wessler, “The Largest Small n-dimensional Polytope with n+3 Vertices,” Journal of Combinatorial Theory, Series A, 102(2), 2003 pp. 401-409.
doi:10.1016/S0097-3165(03)00054-2
[3] A. Klein and M. Wessler, “A Correction to ‘The Largest Small n-dimensional Polytope with n+3 Vertices,’” Journal of Combinatorial Theory, Series A, 112(1), 2005 pp. 173-174.
doi:10.1016/j.jcta.2005.06.001
Комментарии (26)
brainick
01.06.2015 18:44-8Очередной пример псевдонаучной мышиной возни, вытащенной из чулана на б-жий свет «Первым сертифицированным инструктором технологий и учебных курсов компании Wolfram Research на территории Восточной Европы» (особенно важно подчеркивать, что именно первый, дабы быдло знало с кем имеет дело) Осиповым Романом, который будучи «Руководителем IT-подразделения издательства «БАЛАСС».», т.е. попросту сисадмином со знанием английского пытается убедить окружающих с помощью красивых картинок и больших чисел в своей невъеой крутости. Место этой статьи только рядом со статейкой «Корчеватель: алгоритм типичной унификации точек доступа и избыточности»». Тьфу.

OsipovRoman Автор
01.06.2015 19:40+4Спасибо за то, что почитали информацию из моего профиля) Я польщен вашим вниманием.
Поясню для вас немного: «первый» — относится ко времени появления сертифицированных инструкторов.
«Руководитель» — это не системный администратор (мою должность можно назвать с той же легкостью «IT-директор»).
Последнее: я не убеждаю никого в своей крутости) В статьях даже нет упоминания про меня (кроме небольшой строки внизу). Я рассказываю про интересные задачи, которые можно решать с помощью языка Wolfram Language, часть из которых решаю сам, а часть — являются переводами из официальных блогов и журналов Wolfram Research.
brainick
01.06.2015 19:26-4>>>Несколько месяцев моё лучшее решение для 11 точек было в асимметричном локальном максимуме. <<<
ЩИТО??? Расскажите мне сущеглупому смысл этих слов.
>>>13-НММ имеет вершину в точке 13 и содержит в себе несколько КРИВОВАТЫЙ семиугольник 12-8-10-6-7-9-11<<<
Кривоватый!!! Карл, в статье, претендующей на то, чтобы быть математической, используется слово «кривоватый». На Хабре, Карл!!!
OsipovRoman Автор
02.06.2015 12:32Спасибо за то, что указали на неточности перевода. Эти места скорректированы.

ripatti
02.06.2015 01:20+1Я так понял, для 6, 7, 8, 9 и 16 автор нашел глобальный оптимум, а для остальных — просто хорошие решения (пока не понятно глобальный это оптимум или нет). И что оптимальность следует из существования некого root object.
Кто-нибудь на пальцах может объяснить что такое root object и как оно доказывает, что решение оптимально?
OsipovRoman Автор
02.06.2015 07:18Root object — это специальная конструкция в языке Wolfram Language, основанная на функции Root.
Root[f, k] задает k-й корень полиномиального уравнения f[x]=0.
Этот символьный объект является аналитическим и Wolfram Language может производить множество различных вычислений, опираясь на его свойства. Эти объекты служат для представления решений полиномиальных уравнений степени выше 4-й, которые по теореме Абеля — Руффини не могут быть решены в радикалах. Если посмотрите на решение Эда Пега, вы увидите и полином f и номер корня k. Полином представляется в виде чистой функции с аргументом #1 (аналог x, по сути).
Простой пример:

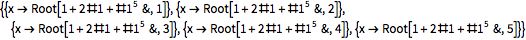

ripatti
02.06.2015 18:32Ладно, хорошо, теперь это понятно. Теперь я даже вижу в статье полиномы с дикими коэффициентами. А откуда берутся эти полиномы и как они соотносятся с многогранниками? И почему в полиноме 16 степени мы берем именно 5й корень, их же там целых 16? Желательно тоже на пальцах, если не затруднит.
Еще в тексте фигурирует некий параметр r, но определения того, что это такое, я в статье не нашел.

mkot
02.06.2015 09:58+1Как бы то ни было
Возведение числа в квадрат, которое больше или меньше единицы, даст большее или меньшее число соответственно.
-3 < 1, но (-3)^2 > 1.
Для правильного тетраэдра с объёмом в sqrt(2)/12= 0.117851 потребуется четыре точки.
Перевод совсем не ОК, лучше «для четырёх точек решением будет правильный тетраэдр». Так как мы фиксируем точки и ищем решение, а не наоборот.
Для правильной пирамиды с единичным перпендикуляром потребуется 5 точек, а её объём равен sqrt(3)/12 = 0.1443375; это решение было получено в 1976-ом году [1].
Тут перевод даже не близок к оригиналу, там:
Five points need a unit equilateral triangle with a perpendicular unit line, with volume Square root of 3/12 = 0.1443375; solved in 1976 [1].
Где вы увидели пирамиду? Тут рассказано про конструкцию по ссылке [1], где берутся два «перпендикулярных» симлекса на трёх и на двух вершинах с единичными сторонами и рассматривается их выпуклая оболочка.
brainick
02.06.2015 10:17И ещё раз скажу. Эта статья классический пример псевдонауки, к тому же переведенной в стиле Промта начала 2000-x без малейшего понимания о чём в статье речь – а иначе быть и не могло в силу того, что переводчик, очевидно, не является специалистом по геометрии.
Цитата из статьи>>Для того чтобы найти их самостоятельно, сперва я выбрал наилучшие варианты из более чем тысячи, а затем использовал алгоритм имитации отжига (simulated annealing) (вероятностная задача поиска хорошего приближения к глобальному оптимуму данной функции в широком пространстве поиска – прим. пер.) для улучшения результатов. Для каждой из точек оптимальных решений я перебирал пространство вокруг этих точек для поиска лучшего решения, ненамного их смещая. Затем я ещё более уменьшал пространство поиска, и так из раза в раз. Некоторые из решений, казалось, стремятся к взаимной симметричности. К примеру, для семи точек лучшее решение стремилось к этому многограннику со значением r около половины, который представляет относительный размер верхнего треугольника ?456.
<<
Иначе как цифровым онанизмом эти игры с Mathematic'ой назвать нельзя.
А то, что переводчик этой галиматьи (и еще кучи другой, вроде статьи про арбелос) вдруг стал номером 1 на Хабре — просто позор для Хабра. Хотя в принципе в этой статье отражается модель всей российской науки — пишем чушь, выдавливаем оппонентов, на критику не отвечаем.
OsipovRoman Автор
02.06.2015 12:42Вы можете говорить что угодно, это ваше личное субъективное мнение, высказанное в классической манере интернет-хама. Единственное ваше желание — хамить, спровоцировать на ответную негативную реакцию. Именно поэтому вы пишите брызжущие слюной комментарии, в отличие от, скажем, mkot, указавшего выше на конкретные огрехи нашего с Кириллом перевода, которые мы исправим. У вас ничего не получится, можете не стараться, меня из себя вы не выведите)

mkot
02.06.2015 13:23Если по-честному, то ваши переводы действительно требуют серьёзной доработки.
Вот наугад взял:
половина огромного ромбокубоктаэдра
Что-такое огромный ромбокубоктаэдр? В оригинале great rhombcuboctahedron. Слова great и small рядом с телами обычно переводят как большой и малый. Дальше, почему половина тела? На что это должно быть похоже? Снова в оригинале было half the vertices of. То есть особым образом выбранная половина вершин. И т. п.
На самом деле ваши статьи гораздо бы улучшились и их бы стало приятнее читать, если бы их кто-нибудь, кто хорошо разбирается в теме, вычитал бы перед публикацией.
brainick
02.06.2015 14:29-1Некоторые объективные факты.
1. Горячо любимый вами Ed Pegg Jr, хотя и является магистром в области математики, профессиональным математиком вообще и геометром в частности не является. Не является он также и PhD. www.mathpuzzle.com/Resume98.htm
2. Область интересов Ed Pegg Jr — математические игры и развлечения, в общем популяризация математики. Это неплохо, такие люди нужны, но к профессиональной математике он отношения не имеет.
3. Вас, Роман, насколько ясно из вашей биографии, тоже к профессионалам в математике (и в теории многогранников )отнести нельзя. Поэтому получилось вот что. Ed Pegg Jr написал тонну математического мусора, приправ её для солидности ссылками на действительно серьёзные результаты, а вы, поверив его авторитету, решили сделать перевод. В результате на бессмысленную статью еще и наложился дилетантский перевод. Но вы, в силу эффекта Даннинга-Крюгера, понять это не в силах. Поскольку Роман, вы, как я понимаю живете в Москве, то можете попробовать показать эту статью геометрам из МГУ или НМУ и выслушать их мнение.
К слову, вот пример реально хорошей статьи по вычислительной геометрии написанной профессиональным математиком. habrahabr.ru/post/220909
Смотрите и учитесь.
P.S. И ещё. Вы, Роман, пишете, что «задачи, которые можно решать с помощью языка Wolfram Language, часть из которых решаю сам». Как-то раз я смотрел темы курсовых работ для студентов кафедры компьютерных методов физики МГУ. Там есть множество интересных тем, например, задачи начиная с 83 cmp.phys.msu.su/sites/default/files/Plokhotnikov_themes_2nd_hard.pdf
Вот бы и показали всю мощь Matematikи на этих задачах. (Не сомневаюсь, что вашим ответом будет «Не указывайте мне что делать, у меня нет времени, с чего это ради я буду делать это бесплатно и т.д.»)
P.P.S. Если будете переводить статьи ещё, а ясно, что будете, показывайте сначала более-менее профессиональным математикам.
OsipovRoman Автор
02.06.2015 16:20-2Вы видимо знаете мою биографию лучше меня. Если вы считаете себя великим математиком, напишите статью, покажите сами класс) А то, насколько я вижу, вы только занимаетесь критиканством других, прячась за своей анонимной страничкой, не содержащей никакой информации о вас. Приведите свою оф. страницу, список ваших опубликованных работ, должность, организацию, фото, ваш город и пр., чтобы мы могли оценить ваш уровень профессионализма. Информация обо мне представлена наиболее полно в LinkedIn (за исключением последней должности в Баласс, которая еще не описана) ru.linkedin.com/in/osipovroman
brainick
02.06.2015 16:31Читаю на linkedin. Роман Осипов Администратор Русскоязычной поддержки продуктов Wolfram Research. Так я про то и говорю, что вы не математик.
>>Если вы считаете себя великим математиком, напишите статью, покажите сами класс)<< Где я писал, что я великий математик? Нет, я не великий математик, но слава б-гу моего образования хватает, чтобы отличить черное от белого. А когда мне не будет хватать знаний я обращусь к экспертам, но я никогда не буду писать статьи по теме, в которой понимаю как представитель семейства нежвачных парнокопытных в растении семейства рутовых.

OsipovRoman Автор
02.06.2015 17:23Ок, аноним brainick.
P.S. Потрудитесь почитать мой профиль дальше первой строчки.brainick
02.06.2015 18:04ОК. Читаю дальше первой строчки.
Вы сделали:
— импорт и обработка данных из таблиц MS Excel (таблицы среднего размера 600000x25);
— Рисунки для учебников алгебры 5-11 классов
— динамично развивающееся сообщество ВКонтакте
Написали массу статеек, из которых приличными являются лишь 2, но написаны они в соавторстве из 5-7 человек и степень вашего участия в них оценить трудно
Synthesis and Structure of Complex Compounds of Lanthanum, Europium, and Scandium Iodides with Antipyrine
Russian Journal of Inorganic Chemistry
2009 Авторы: Роман Осипов, N. S. Rukk, A. S. Antsyshkina, G. G. Sadikov, V. S. Sergeenko, A. Yu. Skryabina, L. Yu. Alikberova
Deca(hydroxo)-23-Aqua-Hexa(lanthanum(III))Iodide Octahydrate and Deca(hydroxo)-23-Aqua-Hexa(neodymium(III)) Iodide Octahydrate: Syntheses and Structuresa
Russian Journal of Coordination Chemistry
2009 Авторы: Роман Осипов, N. S. Rukk, D. V. Al’bov, A. Yu. Skryabina, L. Yu. Alikberova.
не говоря о том, что они написаны 6 лет назад
а также являетесь членом (гусары молчать!) Межрегиональной общественной организации «Женщины в науке и образовании».
Диссертацию как я понял вы не защитили, что не мешает вам упоминать её так, как будто она защищена.
Что из вышеперечисленного делает вас специалистом по геометрии?
OsipovRoman Автор
02.06.2015 18:26Утомили вы меня уже выцеплять только удобные вам куски, чтобы выдрав их из общего контекста и содержания подать так, как вам нужно.
Если бы вы потрудились погуглить, вы бы нашли, что это за общество «Женщины в науке и образовании», организующее ежегодную международную конференцию «Математика. Компьютер. Образование» www.mce.biophys.msu.ru при поддержке огромного количества уважаемых организаций и деятелей науки и образования. Если вы думаете, что такой умный и пошутили о названии этой организации первым — о, вы сильно ошибаетесь.
Что касается кандидатской — я никогда не говорил, что она была защищена и что у меня есть к. ф-м. н.
Мое общение на этом с вами окончено. На дальнейшие комментарии с вашей стороны отвечать не буду, потому что смысла тратить на вас время, объясняя кто я и чем занимаюсь — не вижу вообще.
Распинаться перед интернет-троллем-анонимом у меня желания больше нет. Удачи.brainick
02.06.2015 19:06Эк вы ловко предлог нашли чтобы слиться. Разве имеет значение мое имя? Или вы как Д'Артаньян в белом ведёте дискуссии только с лицами дворянского происхождения?
Задаю ещё раз вопрос, прямо и чётко.
Зачем не являясь специалистом в геометрии, а следовательно, и не имея возможности правильно оценить статью и правильно ее перевести вы беретесь за столь тяжкий для вас труд?
P.S. В вас Роман, как в зеркале отражается вся российская наука — отсутствие реальных результатов, псевдостатьи или статьи с 7 авторами, возвеличивание каких-то детсадовских результатов вроде иллюстраций в книгу или настройки импорта таблиц, участие в псевдоконференциях со статьями, в которых рисуются пляшущие человечки (http://www.mce.su/archive/doc57344/doc.pdf), дилетантизм, отсутствие самокритики и реакция по типу «сам дурак». Тоже прекращаю с вами разговор, ибо доказать что-то человеку, находящемуся на вашем уровне (полушарлатанском) невозможно.
LeonidShifrin
02.06.2015 20:56+2А со мной вы будете разговаривать?
Мне кажется, вы слишком строги к Роману и выставляете слишком высокую планку для публикуемой здесь информации. Насколько я могу судить, Хабр не является научной площадкой. Учитывая, что авторство статей (тех, о которых идет речь) принадлежит не Роману, критиковать можно две вещи: качество перевода и процесс отбора информации. По переводу, насколько я вижу, Роман принимает и учитывает замечания. По отбору — в конце концов, это его дело.
Я понимаю ваше стремление увеличить плотность информации и отношение сигнал / шум, но на таких ресурсах как Хабр, мне думается, это lost cause (да и вообще, задача совсем не из простых, и в первую очередь должна решаться создателями площадки, а не блоггерами, на таких площадках как Хабр). Я мог бы перечислить несколько причин, почему это так (как мне представляется), но скажу лишь, что, по моему мнению, это прямо заложено в бизнес и социальную модель Хабра и вполне устраивает его создателей. Это вполне в духе времени, нравится это или нет. Пытаться превратить площадку в то, чем она не является — неблагодарный труд. В конце концов, никто не мешает попробовать организовать площадку, где будут действовать другие правила, и сделать ее успешной и посещаемой.
Возвращаясь к постам этого блога, я бы посоветовал в первую очередь рассматривать их как иллюстрации к применению функционала Wolfram Mathematica, рассчитанные на широкую (и потому разно-уровневую, и в целом не очень взыскательную) аудиторию. Есть два подхода к подаче информации: можно либо предоставлять много разного и давать каждому возможность решать, что ценно, а что нет, либо давать «избранное», но тогда отбирающий во-многом принимает решение за читателя. И раз уж вы заговорили об отечественной науке, то позвольте мне, как человеку имевшему дело и с отечественным, и с зарубежным подходом, сказать вот что: во-многом, именно отсутствие упора на «единственном правильном пути к истине» помогает западным ученым выходить на высокий уровень и получать замечательные результаты (сравните, например, лекции Фейнмана с курсом Ландау, для начинающего физика-теоретика).


Alex222
Когда читал подумал что америкосские тексты по математике забавны:
«одно из решений, **вероятно**, лучше остальных»
«получен, **видимо**, хороший результат»
«к большим, *видимо**, можно отнести хексагон Сатурна» (этот тот у которого размер больше диаметра Земли)
(по памяти). Постоянно это «вероятно», «видимо»
Ну, у них это смотрится нормально,
«one is probably better than others»
maximw
При использовании вероятностных алгоритмов справедливо к результату исследования добавлять слово «вероятно».