Управляя чем-либо или кем-либо, как правило, мы не воздействуем на управляемую систему постоянно и в целом. Лишь время от времени мы пытаемся скорректировать её, чтобы в итоге была достигнута желаемая цель. Если быстро определить момент и место, куда должны быть приложены усилия, система незначительно отдалится от планируемого вектора развития и при минимальных затратах вернётся на путь до нужной нам цели.

Как быстро найти те элементы системы, на которые нужно оказать корректирующее воздействие? На этот вопрос мы и попытаемся сегодня ответить.



Решение будем искать не в области сложных алгоритмов, которые часто трудно понять и применить. Мы будем говорить о простых вещах, которые около 70 лет назад, были причиной выхода из кризиса для целой страны. Обсуждаться будет измерение и анализ массовых явлений. Только такие явления будут статистически управляемыми. Почему люди могут считать статистику злом? Порой это связано с тем, что кто-то с умыслом или по глупости неверно делает выводы на её основе. Три примера, с которыми многие сталкиваются в повседневной жизни.

Среднее значение — только верхушка айсберга

Мы считаем средние значения двух выборок с объёмом 50 из двух разных генеральных совокупностей. По случайности они совпали. И это хорошо описывает, то что показывает нам среднее значение, которое очень часто используется для краткого описания систем. Вместо того, чтобы перечислить доходы всех сотрудников или граждан государства, говорят о среднем значении. А как мы поняли, среднее значение может быть одинаковым у разных совокупностей. Также оно может быть одинаковым для одной и той же системы в разные моменты времени. Например, в примере с доходами граждан в государстве мог произойти рост численности среднего класса, а мог произойти рост состоятельности богатых и большее снижение дохода бедных слоёв общества. Таким образом, чтобы хорошо понимать систему нам необходимо знать закон распределения величин в этой системе.

Нужно больше наблюдений

Во-вторых, основу статистического исследования составляет множество данных о измерении одного или нескольких признаков. Реально наблюдаемая совокупность объектов, статистически представленная рядом наблюдений случайной величины, является выборкой. Гипотетически существующая (домысливаемая) — генеральной совокупностью. Если объем выборки достаточно велик (n > ?) выборка считается большой, в противном случае она называется выборкой ограниченного объема. Так вот, выборка считается малой, если при измерении одномерной случайной величины объем выборки не превышает 30 (n <= 30), а при измерении одновременно нескольких (k) признаков в многомерном пространстве отношение n к k не превышает 10 (n/k < 10). Анализируя статистику по малым выборкам, необходимо понимать что статистические расчёты будут иметь большие ошибки.

«Не может быть!»

В-третьих, статистика ничего не говорит об одном конкретном случае. Предположим вы решили сыграть по системе Мартингейла в подбрасывание монеты. Вы знаете, что вероятность выпадения орла или решки 1/2. У вас есть 15000 рублей и вы решаете ставить по 1000 рублей. Вы ставите 1000 рублей всегда на выпадение «орла». В случае выигрыша, вы вновь начинаете со ставки в 1000 рублей, а в случае проигрыша каждый раз удваиваете ставку до тех пор пока не выиграете. Может показаться, что спустя какое-то время вы станете миллионером. Но играя по этой системе игрок не получает преимущества, он всего лишь перераспределяет свой выигрыш: игрок проигрывает редко, но помногу, а выигрывает часто и понемногу. Вам не повезло и четыре раза подряд выпала «решка». Вероятность такого исхода 0,5*0,5*0,5*0,5=0,0625

Это более 6 раз на 100 экспериментов по 4 подбрасывания монеты, почему ваш случай не мог быть одним из 6? Статистика не говорит о том, что 0,0625 это мало и вам должно повезти, она говорит о бесконечно большой серии экспериментов по 4 подкидывания монеты. Закон больших чисел в теории вероятностей утверждает, что эмпирическое среднее (среднее арифметическое) достаточно большой конечной выборки из фиксированного распределения близко к теоретическому среднему (математическому ожиданию) этого распределения. То есть, чем больше серия экспериментов, тем ближе результаты этих экспериментов к расчётной вероятности (в нашем случае 0,0625). Но если происходит конечное и небольшое число экспериментов, то результат может быть любым. Иными словами, сразу же попробовав сыграть еще раз на 15000 по той же схеме, очередной проигрыш по-прежнему будет укладываться в возможное распределение результатов подбрасывания монеты. Стоит отметить, что комбинация из двух проигрышей в результате двух серий по 4 подбрасывания значительно меньше. 0,0625*0,0625=0,00390625 или около 4 на 1000 экспериментов (из двух серий по 4 подбрасывания). Такая вероятность уже повод задуматься о честности игры, но не может быть единственным доказательством её нечестности, так как такой исход возможен.

Перейдём к практике

Всё эти примеры приведены не просто в защиту статистики, но и с целью помочь сделать правильный анализ показателей статистически управляемой системы. Примером управляемой системы в нашем случае будет отдел технической поддержки с 20 специалистами. Для лёгкости понимания, будем считать что они полностью нагружены и решают любые типы проблем, возникающую у разных клиентов. На решение разных типов проблем тратится примерно равное количество времени. В конце месяца получены следующие результаты. Они в отсортированном по возрастания или убыванию виде и будут являться основой для выводов у многих управленцев.

Место	Специалист	Итого обращений, шт	Среднее время на один тикет, мин
1	Иванов	246	39
2	Петров	240	40
3	Чкалов	234	41
4	Федотов	228	42
5	Максимов	222	43
6	Королев	222	43
7	Фролов	222	43
8	Чернов	216	44
9	Белов	216	44
10	Антонов	216	44
11	Григорьев	216	44
12	Ткаченко	210	46
13	Кузнецов	204	47
14	Романов	204	47
15	Смирнов	204	47
16	Васильев	204	47
17	Новиков	198	48
18	Яковлев	192	50
19	Попов	190	51
20	Федоров	142	69

Предположим, начальник отдела решает выдать премию менеджерам в ТОП-3 в размере 20% от оклада и оштрафовать на 20% трёх специалистов с наихудшими результатами. Верно ли так решать вопрос мотивации? Начальник отдела объясняет своё решение желанием предоставить стимул работникам стремиться к лучшим результатам и не оказаться в числе худших. Почему же были выбраны по три специалиста с концов списка? Возможно, потому что это любимое число начальника отдела.

Что будет, если воспользоваться статистикой?



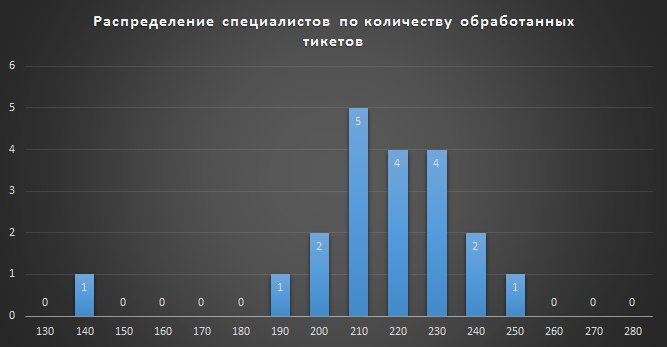
Так выглядит плотность распределения специалистов по числу обработанных обращений. Хорошо заметно, что 19 специалистов образуют выборку, показатели которой хорошо будут описаны нормальным распределением.

Если результат наблюдения является суммой многих случайных слабо взаимозависимых величин, каждая из которых вносит малый вклад относительно общей суммы, то при увеличении числа слагаемых распределение центрированного и нормированного результата стремится к нормальному. Этот закон теории вероятностей имеет следствием широкое распространение нормального распределения, что и стало одной из причин его наименования.

Что это значит с точки зрения статистики и теории вероятности? 19 специалистов работали нормально. Существовало множество явлений (шум, температура в помещении, настроение и другое), каждое из которых в разной степени повлияло на специалистов, что привело к фактическому распределению по результатам. Можно ли сказать что первый в списке работал лучше, чем девятнадцатый, которого хотят оштрафовать? Статистика в данном случае говорит, что разница в результатах их работы может быть вызвана случайными причинами, совокупное воздействие которых некоторые называют удачей. Должна ли удача или неудача быть причиной изменения дохода работника? По-моему мнению, нет. В результате работник не будет чувствовать связи между затраченными усилиями и полученным результатом. Это не позволит создать дополнительных стимулов для повышения эффективности работы.

Что же насчёт двадцатого сотрудника (Фёдоров)? Если мы принимаем гипотезу о том, что результаты сотрудников в нашей системе распределены нормально, вероятность получения любого результата в такой системе будет нам известна. Фёдоров обработал 140 тикетов. Вероятность такого события при нормальном распределении, то есть под совокупным воздействием множества тех же случайных факторов, равна 1 на 10000 экспериментов. У нас остаётся два варианта: либо Фёдорову жутко не везло, либо есть какие-то особые причины (в том числе нежелание работать), которые повлияли на его результаты.

Насколько чувствительны к отклонениям рамки, в которые будут укладываться результаты сотрудников, каждый может выбрать для себя сам, следуя определённым правилам. По принципу контрольных карт Шухарта-Деминга контрольные границы — коридор, внутри которого лежат значения при стабильном (нормальном) состоянии процесса.

Цель построения контрольной карты Шухарта — выявление точек выхода процесса из стабильного состояния для последующего установления причин появившегося отклонения и их устранения. Популярным, во многом благодаря Демингу, является метод 6 сигм.

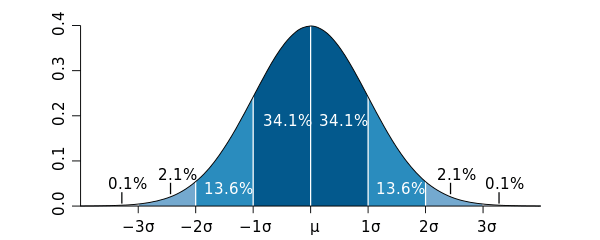
В основе названия метода статистическое понятие среднеквадратичного отклонения, обозначаемого греческой буквой ?. Зрелость процесса в этой концепции описывается как процент элементов системы, показатели которых на выходе укладываются в 99,99966 % плотности нормального распределения. Для целей контроля в этом методе нам важно понять какие контрольные границы мы берём. Явления с какой вероятностью мы будем считать аномальными или в терминах контрольных карт «выбросами» процессов? Общепринятой практикой являются три стандартных отклонения от среднего арифметического. Почему 6 сигм, а не 8 или 4? Возможно, на три умножать удобно и приятно, но главное, что за границами ±3 сигм остаётся действительно малая часть распределения, выброс в которую стоит внимания. Понятно, что отклонение от среднего можно как прибавить, получив верхнюю контрольную границу, так и отнять для получения нижней контрольной границы.



Сделаем контрольную карту для вымышленных результатов работы отдела технической поддержки.



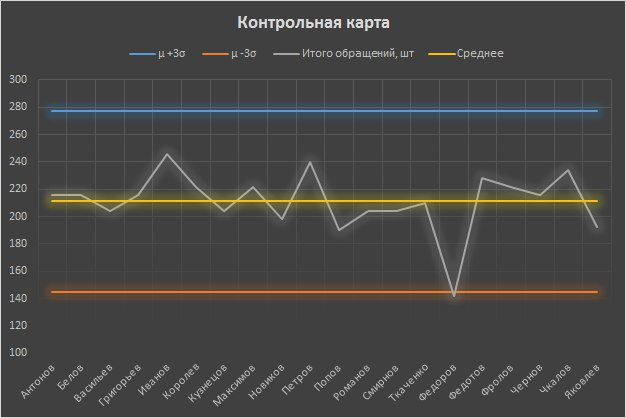
Действительно, Фёдоров показал аномальный результат, который не попал в контрольные границы. Опросив его, начальник должен узнать о причинах такого результата и принять решение о мотивации сотрудника в зависимости от уважительности этих причин. Результаты остальных сотрудников оказались нормально распределены, а значит с точки зрения статистики на них влияло множество случайных факторов. В случае, если какой-либо из работников показал бы выдающийся результат за пределами верхней контрольной границы, это явления также бы требовало изучения на возможность внедрения в большем масштабе.

Однако, принять решение о мотивации сотрудников в конце месяца не лучшее решение. В прошлом изменить ничего уже будет нельзя, а низкие результаты отдельных сотрудников могут повлиять на итоги работы всего отдела. Для того, чтобы вовремя отреагировать и скорректировать вектор развития системы нам нужно больше контрольных карт. Представим, что у нас они есть для каждого сотрудника и наблюдения мы записываем ежедневно.

Посмотрим на контрольную карту Фёдорова, но прежде скажем немного про признаки особой изменчивости процесса, сигнализирующие о нарушении стабильности (управляемости) процесса и появлении особой причины этой изменчивости:

• выход точек за верхнюю или нижнюю границы контрольной карты
• 7 или более точек подряд лежат по одну сторону от средней линии
• более 6 точек монотонно возрастают или убывают

Есть и другие признаки. Установившегося общепринятого набора дополнительных правил чтения контрольных карт нет, поэтому рекомендуется использовать в первую очередь правило Шухарта (выход точек за границы), а все прочие вводить по мере накопления опыта при необходимости.



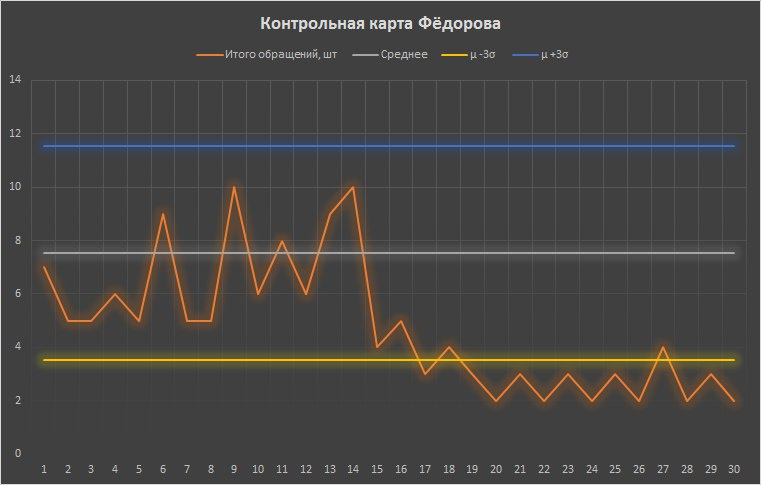
Заметить, что у Фёдорова изменились результаты работы, можно было не только в конце месяца. Уже 17 числа был выброс показателя за контрольные границы. Именно в этот момент начальник отдела должен был заметить сигнал и выяснить причины этой аномалии.

В целом это тема менеджмента качества. Его целью является обеспечение стабильности (управляемости) любых процессов: процесса продаж, управления персоналом, оказания услуг или производства продукции. Приведём пример уже с реальными числами. Как облачный провайдер, мы должны обеспечивать уровень доступности наших услуг SLA не ниже 99,95%. То есть определенная инфраструктура (например, виртуальная машина c определёнными характеристиками) или сервис (например, виртуальный рабочий стол) может быть недоступен для клиента не более 22 минут за весь месяц. Для обеспечения такой надёжности и стабильности выходов из процесса предоставления услуг облачным провайдером строится устойчивая система, которая мониторится с гораздо большей частотой, чем в примере ранее. В основе такой системы оборудование корпоративного уровня, располагаемое в нескольких ЦОДах Tier III, соединённых оптическим кольцом высокой доступности с дублированными каналами, и, конечно, техническая поддержка 24х7. Бизнес облачного провайдера является одним из ярких примеров, когда качество услуг зависит от качества работы компьютерных систем и персонала организации.

Если вам понравилась тема статистического управления процессами, очень рекомендуем прочитать книгу Эдвардса Деминга «Выход из кризиса: Новая парадигма управления людьми, системами и процессами». Деминг впервые посетил разрушенную войной и отсталую Японию в 1946 году. Его лекции по методам статистического контроля качества оказались восприняты высшими руководителями японских компаний. Необходимость изучения и внедрения методов статистического контроля была осознана, и в Японии был организован процесс массового обучения менеджеров. Дальнейшее развития этих методов привело к созданию системы Дао Toyota и философии Кайдзен. Многие считают именно эти методы причиной «японского экономического чуда», которое вывело страну в экономические лидеры. Вот пара цитат из книги «Выход из кризиса», которые побудили нас написать эту статью.

«Ранжирование людей, принадлежащих системе (от выдающихся до худших), противоречит научной логике и разрушительно как политика».

«Руководитель должен уметь при помощи расчетов, если имеются соответствующие данные, или на основе суждения, когда таких данных нет, отличать тех своих работников, которые находятся за пределами системы как в худшую, так и в лучшую сторону, и таким образом требуют либо особой помощи, либо должны быть выделены и поощрены в той или иной форме».