Сейчас компьютеры решают почти любые задачи. Они работают и приносят выгоду практически во всех отраслях. Но давайте посмотрим, что такое компьютер. Это машина, которая манипулирует числами. Подобные манипуляции — практически все, что они могут делать. Поэтому тот факт, что они решают так много задач, просто манипулируя числами, кажется почти волшебным.

Давайте посмотрим, откуда пришли числа, куда они могут привести и как они работают.



В основе статьи — доклад Дугласа Крокфорда (Douglas Crockford) с июньской конференции HolyJS 2017 в Санкт-Петербурге (презентацию доклада можно найти тут)

Пальцы

Начнем с пальцев. Пальцы намного старше чисел. Человек развил пальцы, чтобы лучше лазить по деревьям и собирать фрукты. И он был действительно счастлив, занимаясь этим на протяжении миллионов лет.

Инструменты

Но климат изменился, деревья начали исчезать. Человеку пришлось спуститься на землю, пойти по траве и искать другие источники пищи. И пальцы понадобились для манипулирования инструментами, например, палкой. С ее помощью можно было копать землю, чтобы найти клубни. Еще один пример инструмента — камень, позволяющий колотить клубни, чтобы сделать их достаточно мягкими для еды (наши маленькие обезьяньи зубы не позволяют есть всё подряд; чтобы выжить, мы были вынуждены учиться готовить).

Со временем человек набирался опыта в обращении с инструментами. И инструменты влияли на нашу эволюцию, поэтому мы продолжали их обновлять. Вскоре мы узнали, как делать ножи из вулканического стекла, и в итоге научились управлять огнем. Теперь человек знал, как посадить семена в землю и вырастить свою собственную еду. С новыми знаниями люди начали собираться в более крупные сообщества. Мы перешли от семей и кланов к городам и нациям.

Общество росло, и появилась проблема отслеживания всей человеческой деятельности. Чтобы решить ее, человеку пришлось придумать счет.

Счет

Как оказалось, наш мозг не очень хорошо запоминает много цифр. Но чем сложнее становилось общество, тем больше всего нужно было запоминать. Поэтому человек научился делать зарубки на древесине и надписи на стенах. Появились идеи нанизывать орехи на струны. Но мы все равно забывали, что именно представляют собой эти числа. Поэтому пришлось придумать письменность.

Письменность

Сегодня мы используем письменность для решения множества задач: для писем, для законов, для литературы. Но сначала это были рукописи. Я считаю изобретение письменности самым важным открытием из когда-либо совершенных человеком, и произошло оно трижды.

Первые следы письменности были найдены на Ближнем Востоке. Многие умные люди считают, что это случилось в Месопотамии. Я же думаю, что это произошло в Египте. Кроме того, письменность была изобретена в Китае и в Америке. К сожалению, последняя из упомянутых цивилизаций не пережила испанское вторжение.

Давайте рассмотрим подробнее некоторые исторические системы счисления.

Египет

Так выглядели числа в Египте.


У египтян была десятичная система. Для каждой степени 10 у них был предусмотрен свой иероглиф. Палка представляла единицу, кусок верёвки — 100, палец — 10000, а парень с поднятыми руками — миллион (это демонстрирует некоторую математическую изощренность, т.к. у них был символ, обозначающий не абстрактное понятие «много», а точно «миллион» — ни больше, ни меньше).

Египтяне придумали много других вещей: треугольник 3 на 4 на 5 с прямым углом (они знали, зачем этот угол нужен), действительно умную систему для работы с дробями. У них было приближение для числа Пи и много чего еще.

Финикия

Египтяне научили своей системе финикийцев, которые жили на территории современного Ливана. Они были очень хорошими мореплавателями и торговцами — плавали по всему Средиземному морю и части Атлантики. Приняв от египтян довольно сложную систему счисления, они упростили ее. Используя письменность, состоящую только из согласных букв, они уменьшили набор символов с тысяч, которые были у египтян, до пары десятков, что было намного проще в использовании. И они научили своей системе людей, с которыми торговали, в частности, греков.

Греция

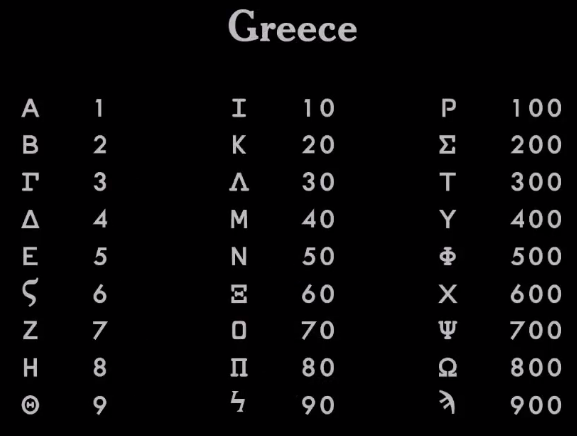
Греки взяли финикийскую систему и улучшили ее, добавив гласные. Поэтому теперь они могли корректно записывать все слова. С того времени греческий алфавит содержит 27 букв.

Греки использовали тот же набор символов для записи чисел. Они взяли первые 9 букв алфавита для обозначения цифр с 1 по 9, следующие 9 букв — для десятков от 10 до 90, и еще 9 букв для сотен — от 100 до 900. Свою систему они передали римлянам.

Рим

Но римляне по-прежнему использовали в основе своей системы счисления египетскую систему. Хотя они переняли греческий подход — использование букв вместо иероглифов. Также они добавили некоторые инновации, чтобы сделать числа немного компактнее.

Одна из проблем египетской системы заключалась в том, что для записи числа 99 требовалась последовательность из 18 символов. Римляне хотели сократить запись. Для этого они придумали символы, представляющие половину десяти или половину сотни (тысячи). Один у них был представлен символом I (или палкой), 10 — X (пучок палок, соединенных вместе), а 5 — V, что есть всего лишь X пополам.

Другая инновация заключалась в добавлении вычитания в систему счисления. До сих пор системы были аддитивными. Число представлялось суммой всех символов. Но у римлян была реализована идея, что определенные символы (на определенных позициях) могут уменьшать число.

Китай

Между тем в Китае творились действительно интересные вещи.


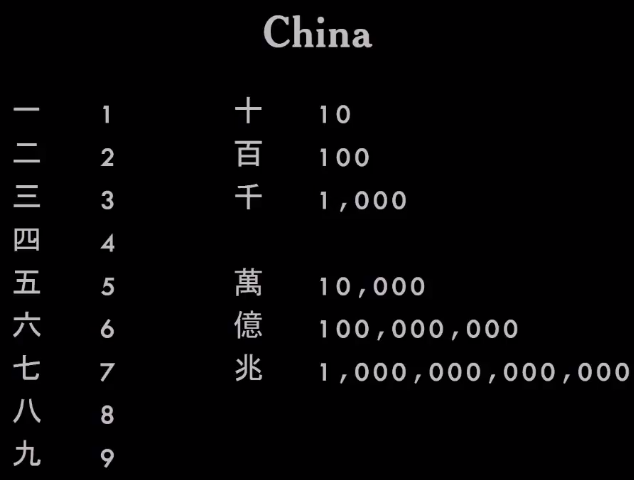
У них была другая система, в которой использовались символы от 1 до 9 и набор множителей или модификаторов. Так можно было записывать числа любого размера и сложности, просто составляя иероглифы вместе. Очень элегантная система.

Индия

Больший скачок произошел в Индии.


Математики в Индии пришли к идее нуля — числа, которое ничего не представляло. И они догадались использовать его на позиционной основе. Для отображения чисел применялись всего 10 символов, но они могли быть объединены для создания любого числа. Это было действительно важной идеей.

Тиражирование идеи

Индийцы передали свою систему персам. Те назвали её индийскими цифрами. А от персов идея попала к арабам. В свою очередь арабы передали ее европейцам, которые и называли такой способ записи арабскими цифрами. Это основная система счисления, которую сегодня использует большая часть мира.

Действительно замечательно то, что вне зависимости от того, на каком языке вы говорите, вы можете понять эти цифры. Запись числа так же универсальна, как и человеческое общение.

Запись чисел и математика

Вот одно и то же число, записанное во всех упомянутых системах.


И все эти системы работали. Они использовались ключевыми нациями и империями на протяжении веков. Поэтому трудно утверждать, что одна из этих систем лучше, чем другая.

Единственное преимущество, которое имела индийская система над всеми остальными, заключалось в том, что можно было взять столбец чисел и сложить их вместе, не используя счеты — с помощью только лишь ручки, бумаги и слегка тренированного мозга. Это нелегко было сделать в любой другой системе.

Сегодня это неважно, поскольку у нас есть компьютеры. Поэтому нет ясного ответа на то, почему мы все еще используем эту систему. Возможно, есть некоторые преимущества ее использования, которые я не могу себе представить, например, в наборе номера телефона. Кажется, что с использованием римских цифр это будет сделать довольно сложно. Но я не помню, когда последний раз набирал номер телефона. Так что, возможно, это уже не имеет значения.

Важная идея заключается в том, что индийские числа научили нас математике.


Это позиционная система. Вы можете взять цифры и поместить их на числовую линию, а дальше просуммировать, цифры в каждой позиции, умножая их на 10 в степени, соответствующей номеру этой позиции. Получается, что индийские числа являются сокращением для полиномов. А полином — действительно важное понятие в математике. Мы получили способ записи чисел. Этого не было в других системах.

Целые числа

Данная система также допускала отрицательные числа.


Мы могли записать число со знаком минус, представив негативные вещи. Эта концепция была бессмысленной в других системах счисления. Мы не могли говорить о негативном в Египте, в этом не было смысла. Но мы можем делать это в индийской системе. И оказывается, есть много интересных вещей, происходящих с отрицательными числами.

Вещественные числа

Мы можем взять числовой ряд и продолжить его в обратном направлении до бесконечности. Используя такую запись, мы получим действительные числа.


Другие системы счисления также могли работать с дробями. Но это всегда были особые случаи. С индийской системой мы можем записывать дроби точно так же, как целые числа — нужна лишь небольшая дисциплина в управлении десятичными знаками.

В оригинальной индийской записи указывалась позиция разделителя с помощью линии сверху.


Но с годами разделительный символ менялся.

В разных странах существуют свои соглашения о том, как следует писать. В одних культурах используется десятичная точка, в других — запятая. И это долго не имело значения. Вы были в своей стране и могли писать числа правильно или неправильно. Но это становится проблемой, когда у вас есть интернет, потому что теперь числа повсюду. Записанное вами число могут увидеть где угодно. И все будут видеть разные вещи — может возникнуть путаница.


Например, в зависимости от того, где вы находитесь и как обучались, первое число на картинке вы можете прочитать как 2048 или 2 и 48 тысячных. И это может оказаться действительно серьезной ошибкой, особенно если речь идет о финансах.

Поэтому я предсказываю, что мир рано или поздно найдет способ выбрать один из вариантов записи. Потому что нет никакой ценности в этой путанице. Однако сложность в выборе одного из вариантов заключается в том, что ни один из них не является явно лучшим. Как мир будет выбирать?

Я предсказываю, что это решите вы. И выберите вы десятичную точку, потому что ее использует ваш язык программирования. А все цифры в мире в конечном счете проходят через компьютерные программы. В конце концов вы просто решите упростить это.

Основание

Все рассмотренные выше системы имеют основание 10. Так записывали числа на Ближнем Востоке и в Китае. Они не общались между собой, но взяли основание 10.

Как это произошло? Они просто посчитали пальцы на обеих руках. И это сработало.

Но есть и другие культуры, которые записывали числа по-другому. Например, в Америке была система счисления с основанием 20. Знаете, как они до нее додумались? Полагаю, это очевидно: они посчитали пальцы не только на руках, но и на ногах. И это тоже сработало. У них была развитая цивилизация. Они выполняли достаточно много вычислений, но использовали основание 20.

Некоторые культуры использовали основание 12. И мы все еще можем видеть их следы в нашем мире. Например, у наших часов основание 12. У нас все ещё 12 дюймов в футах. Мы выучились этому у британцев и до сих пор не можем отказаться от использования подобных усложнений.

Компромиссы: 60

Шумеры использовали основание 60. Да и мы все еще придерживаемся основания 60, верно? Мы так считаем наше время и делаем географические измерения. Географическим приложениям приходится использовать систему координат на базе системы счисления с основанием 60. Это добавляет ненужную сложность.

Как появилось основание 60? Я думаю, когда города росли, они поглощали много мелких поселений, объединяя их в большие. В какой-то момент они попытались объединить сообщество, которое использовало основание 10, с сообществом, которое взяло в качестве основания 12. Наверняка был какой-то король или комитет — кто-то должен был решить, как объединить их. Правильный вариант был — использовать основание 10. Второй вариант — развиваться с основанием 12. Но вместо этого они выбрали худший вариант из возможных — использовали основание, являющееся наименьшим общим кратным. Причина, по которой было принято такое решение, состоит в том, что комитет не мог решить, какой из вариантов лучше. Они пришли к компромиссу, который, по их мнению, похож на то, что все хотели. Но дело же не в том, кто и что хочет.

Надо отметить, что комитеты все ещё принимают такие решения каждый раз, когда выпускают стандарты.

Двоичная система

Действительно интересная вещь, связанная с основанием, — появление двоичной системы. Мы можем взять индийскую систему и просто заменить 10 на 2.


Так мы можем представлять все при помощи бит. И это был действительно важный шаг вперед, потому что позволил изобрести компьютер.

Если мы начинаем говорить о компьютерах, использующих двоичный формат, необходимо вспомнить о знаке числа. Записывать и отображать знак можно тремя способами:

• Знаковая величина (Signed magnitude representation). В этом случае мы просто добавляем дополнительный двоичный бит к числу и решаем, в каком из состояний этот бит соответствует положительному числу, а в каком — отрицательному. И неважно, поставим ли мы этот бит спереди или сзади (это всего лишь вопрос конвенции). Недостатком этого способа является присутствие двух нулей: положительного и отрицательного, что не имеет смысла, поскольку ноль не имеет знака.
  
• Первое дополнение (One’s complement), в котором мы выполняем операцию побитового нет для числа, чтобы сделать его отрицательным. Помимо двух нулей (положительного и отрицательного — как в предыдущем варианте) у этого представления присутствует проблема переноса: при обычном сложении двух чисел, представленных таким образом, для получения корректного результата необходимо в конце добавлять 1 бит. Но в остальном это работает.
  
• Второе дополнение (Two's complement), в котором удалось обойти проблему переноса. Отрицательное N представляется не побитовым отрицанием положительного N, а им же + 1. Помимо отсутствия проблемы переноса мы получаем только один нуль, что очень хорошо. Но при этом мы получаем дополнительное отрицательное число. И это проблема, потому что вы не можете получить абсолютное значение этого числа — вместо этого вы получите то же отрицательное число. Это потенциальный источник ошибок.
  

Каждый из вариантов имеет свои недостатки, в частности, какие-то дополнительные числа. Я думаю, что мы должны взять это дополнительное число (отрицательный 0 или дополнительное отрицательное число из второго дополнения), и превратить его в сигнал о том, что это не число вовсе. Таким образом это позволит нам избежать проблемы, которая проявляется в Java: если мы используем метод indexOf, чтобы найти строку в другой строке, и если она ее не находит, Java не может сигнализировать об этом. Потому что это дурацкая система может возвращать только int, а int может представлять только целые числа.


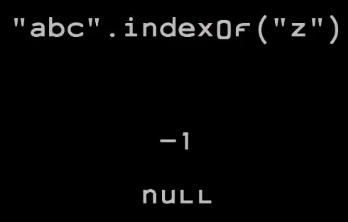
Чтобы обойти эту проблему, придумали сомнительный компромисс: возврат минус единицы. Но, к сожалению, если вы просто возьмете возвращаемое значение и поместите его в другую формулу, можете получить неверный результат. Если бы метод возвращал нулевое значение, это можно было бы обнаружить в downstream, и мы с меньшей вероятностью получали бы плохой результат вычислений.

Types

Давайте немного подробнее рассмотрим типы, использующиеся в наших языках.

int

У нас есть много языков, где под разными именами есть int32. Если мы сложим два числа int32, к какому типу будет относиться результат? Ответ — int33, потому что в результате сложения вы можете получить число, которое немного больше int32.

Здесь Java ошибается. Java говорит, что это int32.

Еще один пример — умножение int32 на int32. Что мы получим в результате? Похоже, int63.


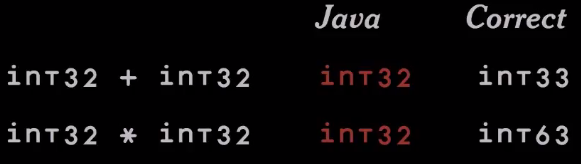
Когда в результате обычного вычисления получается результат, который выходит за рамки типа, мы получаем переполнение. И наши CPU знают об этом. Например, в архитектуре Intel в ЦП есть флаг переноса, который содержит этот 33-й бит. Также на архитектуре Intel, если вы делаете умножение 32-битных чисел, вы получаете 64-битный результат. Т.е. предусмотрен регистр, который содержит необходимые вам «дополнительные» 32 бита. И есть флаг переполнения, который устанавливается, если требуется игнорировать высокий порядок умножения. Он сообщает, что произошла ошибка. К сожалению, Java не позволяет вам получать эту информацию. Она просто отбрасывает все, что является проблемой.

Что вообще должно происходить, при переполнении? Здесь есть несколько вариантов действий:

• мы можем хранить значение null, что, я думаю, очень разумно;
  
• или максимально возможную часть (насыщение — saturation). Это может быть разумно при обработке сигналов и в компьютерной графике. Однако вы не захотите так делать в финансовых приложениях;
  
• можно выдавать ошибку — машина должна вызвать исключение или что-то должно произойти. Софт должен понять, что в вычислениях произошла путаница и нужно исправить ситуацию;
  
• некоторые говорят, что программа должна остановиться. Это довольно резкая реакция, но такой вариант работал бы, если бы машина не просто останавливалась, а как-то сообщала, что что-то не так.
  

Если же вы намерены максимизировать количество возможных ошибок, вы просто отбрасываете самые важные биты без уведомления. Именно так поступает Java и большинство наших языков программирования. Т.е. они предназначены для повышения количества ошибок.

Разбиение чисел на значения из разных регистров

Первые вычислительные машины работали с целыми числами. Но машины были построены и запрограммированы математиками, а они хотели работать с вещественными числами. Поэтому была разработана арифметика, где вещественное число представляется целым числом, умноженным на некоторый масштабный коэффициент.

Если у вас есть два числа с одинаковыми коэффициентами масштабирования, вы можете их просто складывать, а если они имеют разные масштабные коэффициенты, для выполнения простейших операций придется изменить хотя бы один из них. Поэтому перед выполнением каких-либо операций необходимо сопоставлять масштабный коэффициент. И запись стала немного сложнее, потому что в конце вы должны были поставить избыточный масштабный коэффициент. И деление усложнилось, потому что вам приходится учитывать коэффициент масштабирования. В результате люди стали жаловаться, что это сделало программирование действительно трудным, очень подверженным ошибкам. Кроме того, было сложно найти оптимальный масштабный коэффициент для любого приложения.

В качестве решения этих проблем кто-то предложил сделать числа с плавающей запятой, которые могли бы отображать аппроксимированные действительные числа при помощи двух компонент: самого числа и записи того, где находится внутри него десятичный разделитель.

Используя такую запись, можно сравнительно легко делать сложение и умножение. Так вы получаете наилучшие результаты, которые машина может предоставить, используя гораздо меньше программирования. Это был большим достижением.

Первая форма записи числа с плавающей запятой выглядит примерно так: у нас есть некоторое число, значение которого увеличено на 10 в степени логарифма масштабного коэффициента.


Этот подход был реализован в программном обеспечении первых машин. Он работал, но крайне медленно. Сами по себе машины были очень медленными, а все эти преобразования только ухудшали ситуацию. Неудивительно, что появилась потребность интегрировать это в железо. Следующие поколения машин уже на аппаратном уровне понимали вычисления с плавающей запятой, правда, для двоичных чисел. Переход от десятичной к двоичной системе был вызван потерей производительности из-за деления на 10 (которое необходимо иногда выполнять, чтобы нормализовать числа). В двоичной системе вместо деления достаточно было просто сдвинуть разделитель — это практически «бесплатно».

Вот как выглядит стандарт вычислений с плавающей запятой в двоичной системе:


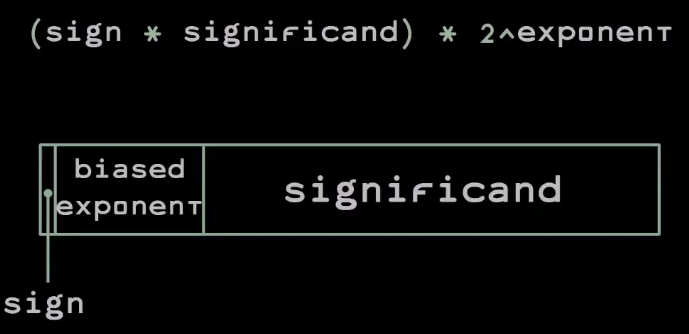
Число записывается при помощи бита знака мантиссы, который равен 0, если число положительное, и 1, если отрицательное, самой мантиссы, а также смещённой экспоненты (biased exponent). Смещение в данном случае играет роль небольшой оптимизации — за счет нее вы можете выполнить целочисленное сравнение двух значений с плавающей точкой, чтобы увидеть, которое из них больше.

Однако с этой записью есть проблема: в ней 0,1 + 0,2 не равно 0,3.


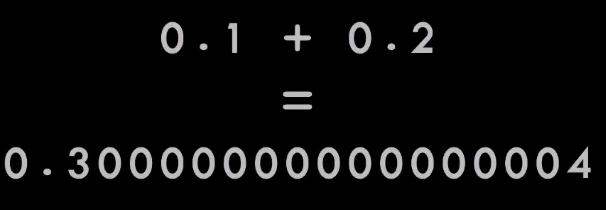
Результат близок, но он неправильный.

Давайте посмотрим, что происходит.


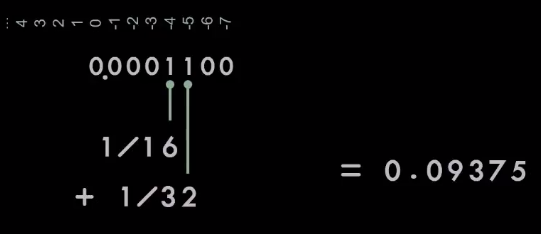
Представим числовой ряд. 0,1 — это приблизительно 1/16 + 1/32, но немного больше, поэтому нам понадобятся ещё несколько бит. По мере движения по числовому ряду мы получим бесконечно повторяющуюся серию 0011, похожую на то, что происходит с 1/3 в десятичной дроби.


Это прекрасно, если у вас в запасе бесконечное количество бит. Если вы продолжите эту последовательность до бесконечности, получите именно то, что нужно. Но у нас нет бесконечного количества бит. В какой-то момент мы должны отрезать этот хвост. И от того, где вы отрезаете, будет зависеть итоговая ошибка.

Если вы отрезаете перед 0, вы потеряете все последующие биты. Поэтому ваш результат окажется чуть меньше, чем нужно. Если вы отрезаете перед 1, по правилам округления необходимо перенести единицу, тогда результат будет чуть больше.


И вы можете надеяться, что в ходе вычислений вы будете немного ошибаться в одну и в другую сторону, а в результате ошибки будут сбалансированы. Но этого не происходит. Вместо этого ошибка накапливается — чем больше вычислений мы делаем, тем хуже результат.

Всякий раз, когда мы представляем константу в написанной на каком-то языке программе или в данных в виде десятичной дроби, мы не получаем именно это число. Мы получаем приближение этого числа, потому что мы работаем с числовой системой, которая не может точно представлять десятичные дроби. И это нарушает ассоциативный закон.

Ассоциативный закон действительно важен в ходе алгебраической манипуляции с выражениями в программах. Но он не соблюдается, если вводы / выводы и промежуточные результаты вычислений не могут быть точно представлены.

А поскольку ни одно из наших чисел не представлено точно, все вычисления ошибочны! Это означает, что (A + B) + C не то же самое, что A + (B + C), что порядок, в котором вы выполняете вычисления, может изменить результат.

Эта проблема не нова. Она была известна еще тогда, когда развивались вычисления с плавающей точкой в двоичной системе — разработчики таким образом шли на компромисс.

В то время были две школы вычислений:

• те, кто занимались научным трудом, писали на Фортране с использованием чисел с плавающей точкой в двоичной системе;
  
• те, кто занимались бизнесом, писали на Cobol, используя двоично-десятичный код (binary coded decimal, BCD). Двоично-десятичный код выделяет 4 бита для каждого числа и ведет обычный подсчет в десятичной системе (используя обычную арифметику).
  

Компьютеры становятся все дешевле, и теперь уже решают практически любые задачи, но мы все ещё застряли в этом шаблоне с двумя разными мирами.

Еще одна проблема представления числа в двоичном формате с плавающей точкой — сложность с преобразованием текста. Берем фрагмент текста и превращаем его в число; затем берём число и преобразуем обратно в кусок текста. Это нужно сделать правильно, эффективно и без сюрпризов, используя как можно меньше цифр. Оказывается, в такой записи это очень сложная проблема, дорогая с точки зрения производительности.

Проблема с типами

В большинстве современных языков программирования присутствует путаница из-за ошибочных типов данных. Например, если вы пишите на Java, каждый раз создавая переменную, свойство или параметр, вам нужно правильно выбрать тип из Bite, Char, Short, Int, Long, Float, Double. И если вы выберете неправильно, программа может не заработать. Причем ошибка проявится не сразу, и в тестах её не будет видно. Она покажет себя в будущем, когда произойдёт переполнение и связанные с этим плохие вещи.

Что может случиться? Одним из самых впечатляющих примеров был отказ Aryan 5. Это ракета, отправленная Европейским космическим агентством. Она сильно отклонилась от курса, а затем взорвалась через несколько секунд после старта. Причиной тому была ошибка в программном обеспечении, написанном на Ада. Здесь я перевел ошибку на Java:


У них была переменная, определяющая горизонтальное смещение. И ее перевели в Short, который переполнился. Результат, попавший в Short, был неправильный. Но он был отправлен в систему наведения и полностью ее спутал, так что курс уже не удалось восстановить. Эта ошибка оценивается примерно в полмиллиарда долларов.

Я полагаю, что вы еще не делали ошибок, которые бы стоили полмиллиарда долларов. Но могли бы (технически это все ещё возможно). Поэтому мы должны попытаться создать системы записи и языки, которые позволяют избежать таких проблем.

DEC64

С точки зрения выбор типа данных при объявлении переменных JavaScript намного лучше — этот язык имеет только один численный тип. Это означает, что целого класса ошибок можно автоматически избежать. Единственная проблема — этот тип неправильный, поскольку это двоичные числа с плавающей точкой. А нам нужны десятичные числа с плавающей точкой, т.к. иногда мы складываем деньги и хотим, чтобы результат имел смысл.

Я предлагаю исправить этот тип. Мое исправление носит название DEC64, это современная запись десятичных чисел с плавающей точкой. Я рекомендую DEC64 в качестве единственного численного типа в прикладных языках программирования в будущем. Потому что если у вас будет только один численный тип, вы не сможете сделать ошибку, выбрав неправильный тип (я думаю, это обеспечит гораздо большую ценность, чем-то, что мы можем получить, имея несколько типов).

Аппаратная реализация DEC64 позволяет складывать числа за один цикл, что снижает значимость производительности при использовании старых типов. Преимущество DEC64 заключается в том, что в этой записи основные операции над числами работают так, как привыкли люди. А устранение числовой путаницы уменьшает ошибки. Кроме того, преобразование чисел DEC64 в текст и обратно — просто, эффективно и не содержит сюрпризов. На самом деле это немного сложнее, чем преобразование целых чисел в текст и обратно — вам просто нужно следить за тем, где находится десятичная точка, и вы можете удалить избыток нулей с обоих концов, а не только с одного.

DEC64 может точно представлять десятичные дроби, содержащие до 16 цифр, чего вполне достаточно для большинства наших приложений. Вы можете представлять числа от 1*10^-27 до 3 с 143 нулями.

DEC64 очень похож на исходные числа с плавающей точкой, разработанные в 40-х годах. Число представлено в виде двух чисел, которые упакованы в 64-битное слово. Коэффициент представлен 56 битами, а показатель — 8 битами.


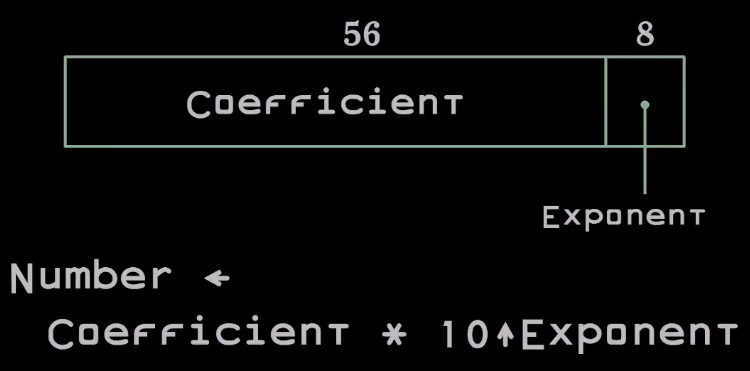
Причина, по которой экспонент находится в конце, заключается в том, что в архитектуре Intel мы можем распаковать такое число практически бесплатно. Это помогает в реализации программного обеспечения.

Если вы хотите посмотреть на программную реализацию DEC64, ее можно найти на GitHub. И если вы думаете о разработке следующего языка программирования, я очень рекомендую вам рассмотреть DEC64 в качестве единственного численного типа.

С форматом DEC64 я не надеюсь попасть в следующий JavaScript, поскольку это фундаментальное изменение. Зная как работает комитет, я не думаю, что это возможно. DEC64 поможет создателю следующего языка программирования (я надеюсь, что JavaScript не станет последним языком программирования — мы не можем оставить его детям; мы должны предложить им что-то другое).

Неопределенности и нули

=Давайте вернемся к числам.

Что такое 0/0?

• Большинство математиков скажут, что это значение не определено, подразумевая, что глупо так делать — такое выражение не имеет смысла (JavaScript определяет это как Undefined). Такая позиция хороша для математики, потому что там все происходит в теоретическом пространстве. Но это не работает для вычислений, потому что если кто-то может подать эти данные на вход машины, та должна как-то отреагировать (вы не можете сказать, что дизайн машины не определён — что-то должно произойти).
  
• Еще одна теория говорит, что машина должна загореться, потому что никто не будет в здравом уме пытаться делить 0 на 0, так что этого никогда не должно произойти. Но мы знаем, что это неправда. Потому что если что-то может произойти, это произойдет.
  
• Другая версия — это должно быть null или какое-то иное понятие, которое говорит, что это не значение. И это разумно.
  
• Еще одна школа считает, что результат должен быть нулевым. Есть математики, которые уверены в этом, но для большинства бизнес-задач такой результат не имеет смысла. Если в прошлом месяце мы продали 0 единиц товара, и общая прибыль по этим единицам составляла 0, какова была средняя прибыль за товар? 0?
  
• Некоторые люди говорят, что это 1, потому что N / N = 1.
  
• Когда-то я работал на мэйнфрейме, где результат был 2. Это была машина, которую создал Сеймур Крей — величайший компьютерный дизайнер в истории. Я ввел 0/0 и получил 2. Могу представить себе диалог в Control Data Corporation. Кто-то сказал: «Сеймур, есть проблема с вашей схемой деления!». «В чем проблема?». «Если кто-то разделит 0 на 0, получит 2!». И Сеймур говорит: «Послушай… Такой операции не должно быть. Ни один разумный человек никогда не должен этого делать. И если я включу дополнительную логику для этого случая, чтобы определить поведение машины, т.е. добавлю ещё одну проверку, она ухудшит производительность для всех, в том числе, для умных людей, которые не выполняют таких операций. И это сделает машину дороже. Я не собираюсь этого делать только из-за того, что какой-то идиот хочет разделить 0 на 0».
  

Также меня интересует, чему равно 0 * n для любого значения n.

Я думаю, что это 0. Но были компиляторы, которые, если встречали в умножении 0, не делали умножение вовсе. Это было большим плюсом к скорости. К сожалению, когда был создан стандарт записи чисел с плавающей точкой, такой подход был объявлен ошибочным, потому что если n является NaN, то результат 0 x NaN не равен нулю.

Почему мы вообще должны заботиться об этом?

Такой код пишут немногие люди, а также многие машины: генераторы кода, макропроцессоры, средства автоматизации — все они будут писать код, вполне может умножить что-то на ноль.

Современные процессоры имеют очень длинные протоколы декодирования команд, которые занимают много циклов. Но они могут быстро перерабатывать множество инструкций, пока нет никаких условных переходов. Если же есть условный переход, все останавливается, пока не будет ясно, в какую сторону двигаться дальше. И это действительно замедляет работу. Есть способ написания кода, когда вы вместо выбора между двумя значениями (условия), выполняется дополнительное действие — умножение на 0 или 1, являющиеся результатом логической операции (того самого условия). Хотя это дополнительная работа, ее исполнение может быть быстрее, чем выполнение кода с условными переходами. Поэтому я рекомендую все операции с 0 (деление, умножение, деление с остатком) приравнивать к нулю.

Как и DEC64, эта идея предложена для следующего поколения прикладных языков программирования.

Вместо заключения

Есть люди, которых я действительно хочу поблагодарить.


Я хочу начать с Леонардо Фибоначчи из Пизы. В конце XII века Леонардо посетил Аравию и узнал удивительные вещи, которые арабские математики воплотили через свою систему счисления — алгебру, геометрию, алгоритмы. Он привез их в Европу и написал книгу, которую опубликовал в 1202 году. В течение следующего столетия эта книга преобразовала Европу. Он создал базу для новых форм банковского дела, что привело к увеличению капитала, подпитывающего Ренессанс.


Я хочу поблагодарить Готфрида Вильгельма Лейбница за отличные вычисления, а также за двоичную систему. Он был первым, кто понял, что можно поставить основание 2 в индийскую позиционную систему счисления. Он думал, что это замечательно. И он был прав.


Я хочу поблагодарить Джорджа Була — английского логика, который разработал алгебру, основанную только на двух значениях — true и false. Булевский тип данных назван в честь него.


Я хочу поблагодарить Клода Шеннона — американского исследователя. Он сделал две потрясающие вещи: во-первых, нашёл соответствие между электроникой и булевой алгеброй, чтобы мы могли преобразовать булеву алгебру в схемы. Именно так создаются компьютеры. Во-вторых, он создал теорию информации, которая гласит, что любой аналоговый сигнал можно превратить в цифровой и обратно с любой желаемой степенью точности. Это утверждение лежит в основе Интернета и всех цифровых медиа: видеороликов, аудио и т.п. Все они возможны благодаря работам Шеннона.


И, наконец, я хочу поблагодарить Техути. Я не смог найти его фотографию, у меня есть только это изображение, которое было вырезано на камне.

Техути изобрёл письмо. Он жил в Египте и понял принцип Ребуса — что вы можете взять изображение чего-либо, поставить в соответствие этому изображению некий звук и дальше использовать эти изображения, чтобы записать созвучия, которые не могли быть представлены картинками. Этот принцип дал начало письму.

Техути был бухгалтером, изобретателем и учителем. Он обучал своей системе письма и создал профессию писцов. Когда писалась мифология Египта, её составители вставили Техути в историю. Они возвели его в ранг бога письма и магии. Он стал очень важной фигурой истории.

Почему они это сделали? Я думаю, по двум причинам. Во-первых, они хотели показать, насколько важна позиция писца. Они поставили главного писца на уровень бога, а другие боги приходили к нему за помощью. А во-вторых, хотели поблагодарить его за то, что он дал им лучшие рабочие места в Египте. Они не занимались сельским хозяйством и не вытаскивали камни, не выполняли другие тяжёлые работы.

Мы — дети Техути. Используем язык программирования для перевода чисел в магию.

---

Если вам понравился этот доклад Дугласа Крокфорда, приглашаем вас на два его новых выступления в рамках грядущей конференции HolyJS 2017 Moscow, которая пройдет в Москве 10 и 11 декабря.

• The Post JavaScript Apocalypse — это его первый доклад, где он расскажет о том, каким мог бы быть язык следующего за JS поколения, а также о новых полезных фишках в ES6.
• Managing Asynchronicity with RQ — второй доклад, рассказывающий о решении, которое призвано повысить простоту использования благодаря минимализму.