Данная статья является переводом статьи, опубликованной в блоге javarevisited. Она может быть интересна как новичкам, так и опытным программистам при подготовке к собеседованиям. В дальнейшем, планируется перевод цикла статей об алгоритмах и рецептах решений проблем как типового, так и академического характера. С удовольствием принимаются конструктивные предложения и замечания как по качеству перевода, так и по выбору новых статей
Нахождение 3-го элемента от конца в односвязном списке или n-го узла от хвоста является одним из каверзных и часто задаваемых вопросов по проблемам односвязных списков на собеседованиях. Задача, в данном случае, в том, чтобы решить проблему всего в один проход цикла, т.е., нельзя снова пройтись по связному списку и нельзя идти в обратном направлении, т.к. список односвязный. Если вы когда-нибудь решали проблемы связных списков, например, нахождение длины, вставки или удаления элементов, вы должны уже быть знакомы с вопросом обхода списков. В данной статье мы используем тот же самый алгоритм, который мы использовали для нахождения срединного элемента связного списка в один проход цикла. Этот алгоритм также известен как «алгоритм черепахи и зайца» из-за скорости двух указателей, используемых алгоритмом для обхода односвязного списка.
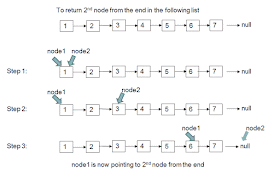
Если вы помните, алгоритм использует два указателя — быстрый и медленный. Медленный указатель начинает обход, когда быстрый достигает N-ого элемента, например, для нахождения 3-го элемента от конца, второй указатель начнет обход, когда первый указатель достигнет 3-го элемента.
После этого, оба указателя двигаются на один шаг за итерацию, пока первый указатель не будет указывать на null, что говорит о достижении конца связного списка. В этот момент, второй указатель указывает на 3-й или N-й узел от конца. Проблема решена, вы можете либо вывести значение узла, либо вернуть ссылку вызывающей стороне в соответствии с вашими требованиями.
Это одна из многих проблем структур данных и и алгоритмических проблем, с которыми вы столкнетесь на типичном собеседовании (см. Cracking the Coding Interviews). Поскольку связанный список является популярной структурой данных, вопросы по нахождению в цикле и определению длины связанных списков, так же как и освещаемый в данной статье, довольно популярны.
Программа на Java по нахождению N-го узла от хвоста связанного списка
Далее приведен полный листинг программы на Java по нахождению N-го элемента от конца односвязного списка. Данная программа решает задачу в один проход, т.е., обход связного списка производится только один раз. Как вы видите, мы использовали всего один цикл while в методе getLastNode(int n). Данный метод принимает целочисленный параметр и может использоваться для нахождения n-го элемента от конца связного списка, например, для 2-го элемента от хвоста, необходимо 2 шага, а для получения 3-го элемента списка — 3.
Класс SinglyLinkedList представляет собой односвязный список в Java. Это тот же класс, который мы использовали ранее в статьях об односвязных списках, например, о реализации связного списка в Java. Это коллекция класса Node, представляющего собой узел связного списка. Он содержит часть данных и ссылку на следующий узел. Класс SinglyLinkedList также содержит ссылку на голову, т.е. первый узел связного списка.
Далее приведено визуальное объяснение нахождения 2-го элемента от хвоста односвязного списка. Видно, как быстрый и медленный указатели проходят по списку, и когда быстрый указатель указывает на хвост, медленный указывает на n-й узел от конца.
Как программист, вы должны знать основные структуры данных и алгоритмы, например, что такое связный список, ее достоинства и недостатки и когда его использовать, например, он хорош для частого добавления и удаления элементов, но уже не так хорош для поиска, т.к. поиск элемента в связном списке занимает O(n) времени. Вы можете прочесть больше о связных списках в хороших книгах о структурах данных и алгоритмах, как, например, Введение в алгоритмы Томаса Х. Кормена — одной из лучших книг для изучения этой темы.
Поначалу, вам может не понравиться эта книга, так как ее немного трудно понять из-за темы и стиля изложения, но вы должны следовать ей и обращаться к ней время от времени, чтобы понимать ключевые структуры данных, например, массивы, связные списки, деревья и т.д.
N-й узел от конца в односвязном списке
public class Practice {
public static void main(String args[]) {
SinglyLinkedList list = new SinglyLinkedList();
list.append("1");
list.append("2");
list.append("3");
list.append("4");
System.out.println("связный список : " + list);
System.out.println("Первый узел от конца: " + list.getLastNode(1));
System.out.println("Второй узел от конца: " + list.getLastNode(2));
System.out.println("Третий узел от конца: " + list.getLastNode(3));
}
}
/**
* Реализация структуры данных в виде связного списка на Java
*
* @author Javin
*
*/
class SinglyLinkedList {
static class Node {
private Node next;
private String data;
public Node(String data) {
this.data = data;
}
@Override
public String toString() {
return data.toString();
}
}
private Node head; // Голова - это первый узел связного списка
/**
* проверяет, пуст ли список
*
* @возвращает true если связный список пуст, т.е., узлов нет
*/
public boolean isEmpty() {
return length() == 0;
}
/**
* добавляет узел в хвост связного списка
*
* @param data
*/
public void append(String data) {
if (head == null) {
head = new Node(data);
return;
}
tail().next = new Node(data);
}
/**
* возвращает последний узел или хвост данного связного списка
*
* @return последний узел
*/
private Node tail() {
Node tail = head;
// Находит последний элемент связного списка, известный как хвост
while (tail.next != null) {
tail = tail.next;
}
return tail;
}
/**
* метод возвращающий длину связного списка
*
* @return длину, т.е, число узлов в связном списке
*/
public int length() {
int length = 0;
Node current = head;
while (current != null) {
length++;
current = current.next;
}
return length;
}
/**
* получения n-го узла от конца
*
* @param n
* @return n-й узел от последнего
*/
public String getLastNode(int n) {
Node fast = head;
Node slow = head;
int start = 1;
while (fast.next != null) {
fast = fast.next;
start++;
if (start > n) {
slow = slow.next;
}
}
return slow.data;
}
@Override
public String toString() {
StringBuilder sb = new StringBuilder();
Node current = head;
while (current != null) {
sb.append(current).append("-->");
current = current.next;
}
if (sb.length() >= 3) {
sb.delete(sb.length() - 3, sb.length());
}
return sb.toString();
}
}
Вывод
связный список: 1-->2-->3-->4
первый узел от конца: 4
второй узел от конца: 3
третий узел от хвоста:
Вот и все о нахождении 3-го элемента с конца связного списка в Java. Мы написали программу, решающую задачу в один проход с использованием подхода с двумя указателями, также известного как алгоритм зайца и черепахи, т.к. один указатель медленней второго. Это один из полезных приемов, т.к. вы можете использовать такой же алгоритм для определения цикла в связном списке, как показано тут. Вы также можете творчески подойти к использованию этого алгоритма при решении других проблем, когда необходим обход по связанному списку и манипулирование узлами одновременно.
Комментарии (21)

izzholtik
21.12.2017 18:01+1Если расстояние между «быстрым» и «медленным» элементами достаточно велико, поимеете постоянные промахи кэша и, грубо говоря, удвоение обращений к медленной памяти.
Вообще говоря, список, не хранящий количество элементов, — это немного негуманно.
izzholtik
21.12.2017 18:11Мдэ
Я попробовал ткнуть простейшим бенчмарком, чтобы это увидеть, и обнаружил, что у вас квадратичная сложность добавления элемента, и больше 20000 за вменяемое время добавить проблематично. Не надо так делать.staticlab
21.12.2017 20:44Кстати, хорошая задача на собеседование для джуниоров: что не так с этим кодом добавления элементов?

Lure_of_Chaos
23.12.2017 20:25А на собеседовании не редкость последовательность вопросов: 1. напишите код, решающий какую-то задачу. 2. как можно улучшить этот код?

xmetropol
22.12.2017 02:45Ну так если хвост списка определять путём пробега всего списка от головы и до, собственно, хвоста. Ничего удивительного, что вставка элементов в конец списка так затрагивает производительность. Тут бы указатель на хвост хотя бы иметь, ладно уже там колличество)))

izzholtik
21.12.2017 18:44+2Все ведь любят графики?
По вертикали — время в мс, по горизонтали — расстояние между элементами. Размер списка — 30000000.
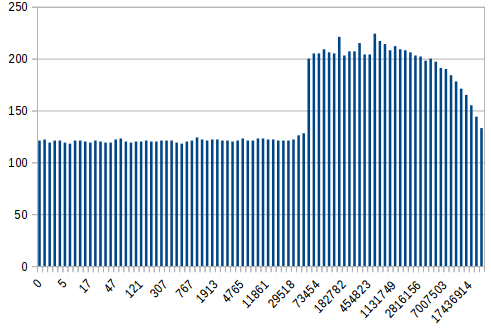
Кстати, кто из ЦА статьи ответит, почему в конце график снова идёт вниз? :D
poxvuibr
22.12.2017 10:00График идёт вниз, потому что устал :). У меня к нему другой вопрос. Почему он так резко скакнул вверх? Что там случилось? Такое впечатление, что в игру вступил какой-то внешний фактор, который постепенно сошёл на нет. Такое поведение воспроизводится?

izzholtik
22.12.2017 10:54Да, вполне. Я смотрел этот участок отдельно. Не так резко, как кажется, но за ~150 элементов время обработки практически удваивается.

poxvuibr
22.12.2017 12:32А кода, который делает этот график вы не выкладывали? Я бы у себя попробовал.

izzholtik
22.12.2017 13:22Не то чтобы оно претендовало на бытие бенчмарком.
https://paste.ubuntu.com/26232091/
График строился в экселе.

bearded_guy
22.12.2017 19:26Если испытания происходили последовательно, то мб все страницы попали в страничный кеш?

soft-ice
22.12.2017 02:45Если список окажется зацикленным на каком-либо элементе, то алгоритм уйдет в небытие.

caesar_84 Автор
22.12.2017 03:07Уважаемые комментаторы, я автор не статьи, а перевода. В любом случае, спасибо за замечания, они будут учтены как в части моего обучения, так и при комментировании в блоге автора статьи. Кстати, осмелюсь предположить, что приведенный код класса SinglyLinkedList условен и не является образцом для подражания.

Lure_of_Chaos
23.12.2017 20:28Уважаемый переводчик, а минусы огребаете Вы. Учтите, пожалуйста, этот момент в последующих переводах :)

pozitrone23
25.12.2017 16:04Мне неприятно что в коментах люди вечно обсирают автора. Варварство

poxvuibr
25.12.2017 16:13Действительно варварство. Хорошо, что в комментариях к этой конкретной статье никто ничего плохого про автора не сказал.


fzn7
Не очень понял как соотносится формальный запрет на несколько проходов по списку и наличие 2х итераторов.
alexxisr
вот да — чем это отличается от «посчитать кол-во элементов в списке, потом дойти до нужного»? кол-во операций такое же получается.
niamster
Локальностью данных. Если данные не локальные или не помещаются в кэш первого уровня.
Хотя если честно все подобные задачи имеют академический характер в 80% случаях.
poxvuibr
При чём тут локальность данных? Это же linked list.
igormich88
Ну по идее для честного одного прохода проще использовать очередь на N элементов. Но это в том случае когда N не большое.