02.01.2018 13:28
Rumyantsev 23 4400 Источник

Введение


В предыдущей части рассматривалась принципиальная возможность кодирования при котором, в случае, если можно выделить общую часть у ключа и сообщения, то передавать можно меньше информации чем есть в исходном сообщении.


image

Позвольте немного расскажу откуда вообще взялась эта тема. Давным-давно от одного хорошего человека- ivlad взял почитать и вот пока никак не отдам (прости пожалуйста) интересную книжку [1], где, написано: «в свою очередь криптография сама может быть разделена на два направления, известные как перестановка и замена».

Соответственно почти сразу появились следующий вопросы:


  • т.к. перестановка и замена сохраняют количество информации, то можно ли сделать так, чтобы обойти это ограничение, и передавать информации меньше чем есть в сообщении, — отсюда (из «а не слабо ли») родилась первая часть;
  • если задача выглядит решаемой, то есть ли само решение и хотя бы толика математического смысла в нём – этот вопрос и есть тема этой части;
  • есть ли во всём этом практический смысл – вопрос пока открыт.

Что общего у ворона и письменного стола?


Загадка Кэрролла в заголовке дана как иллюстрация проблемы, которую необходимо решить. А именно: определить пару функций $E(k,m)$ — кодирования и $D(k,с)$ — декодирования, удовлетворяющих следующим условиям:


  • $I(E(k,m)) \le I(m)$ –объём передаваемой информации по Шеннону меньше объёма информации в исходном сообщении
  • $D(k,E(k,m))=m$ – функция декодирования, применённая к закодированному сообщению, позволит однозначно восстановить исходное сообщение.

Здесь $I(m)$ – объём информации по Шеннону [2] (в предположении, что все символы встречаются равновероятно, что в общем случае неверно, но для используется для простоты изложения) в сообщении $m$, $k$ — ключ, $с = E(k,m)$ – закодированное сообщение.


Для того, чтоб упростить себе дальнейшие рассуждения давайте ограничимся в дальнейшем сообщениями, которые можно привести в числовую форму, что с одной стороны нас не особо ограничивает (т.к. любому символу можно присвоить соответствующий числовой код), а с другой позволит воспользоваться математикой в нужном объёме.


Итак, рассмотрим сначала для примера два числа $k= 746 130$ и $m = 50 133 666$ и, воспользовавшись основной теоремой арифметики [4] (любое натуральное можно разложить на произведение простых) найдём следующие параметры:


  • Наименьший общий делитель $k$ и $m$ – $НОД(k,m) = 1 254$, его простые делители $[2,3,11,19]$,
  • Частное $m/НОД(k,m) = 595$ и его простые делители $[5,7,17]$, которое обозначим как $с_0$,
  • Разложение числа $m$ на простые множители: $[2,3,11,19, 39 979]$,
  • Разложение числа $k$ на простые множители: $[2,3,5,7,11,17,19]$.

Запишем всё это в табличном виде, где синим помечена общая часть информации между ключом и сообщением, жёлтым — информация уникальная для ключа, оранжевым – уникальная для сообщения:


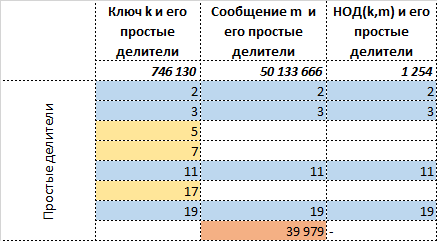
image

Сразу же становится видно, что $НОД(k,m)$ представляет из себя общую часть между ключом $k$ и сообщением $m$, которая есть и у отправителя и у получателя. Таким образом, в идеале конечно, а не в реальности, достаточно передать информацию об:

  • уникальной для сообщения информации — том, что не относится к $k$ т.е. $[39 979]$, а именно $с_0 = 39 979$,

  • самом $НОД(k,m)$, но так, чтобы его нельзя было бы восстановить.

Пометим теперь позиции простых делителей $НОД(k,m)$ общие с простыми делителями $k$, единицами, а остальные, кроме, может быть ведущей позиции – нулями.


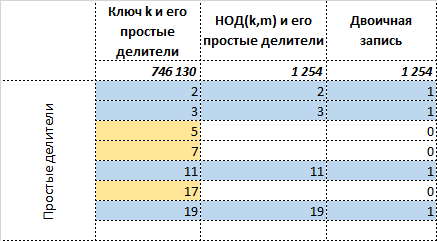
image

Получившееся число $с_1 = 1010011 = 83$ в достаточной степени характеризует $НОД$, позволяя тем самым восстановить исходное сообщение. Т.е. получив на вход два числа $[39 979, 83]$ необходимо сделать достаточно простое обратное преобразование:

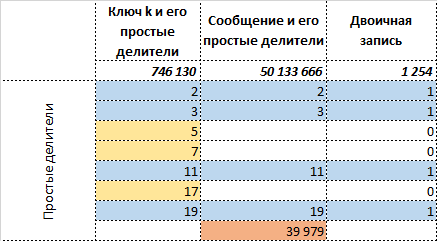
image

Если теперь оценить длину исходного сообщения в двоичном виде $len_2(m) = len_2([1111010000011100100000100])= 26$ и сообщения $len_2([c_0,c_1])= len_2([1001110000101011, 1010011]) = 23$, то видно, что можно получить экономию длины сообщения в $3$ бита, то же самое и с количеством информации $I(m) = 13$ бит, $I(c)=I([c_0,c_1])=11.5$ бита. Здесь функция $len_2(\cdot)$ — длина числа в двоичном виде.

image

Таким образом, выражаясь словами из известного анекдота «в Шотландии есть как минимум одна овца, черная как минимум с одной стороны» [3].

Итак, что на данный момент имеем — данный способ кодирования подходит, но только для пар чисел, имеющих в разложении одинаковые делители. В противном случае, если, например, взять в качестве ключа и в качестве сообщения простые числа, то очевидным образом мы ничего сократить не сможем, а только увеличим и длину сообщения, как и количество передаваемой информации, а это вовсе не то, чего добивались. Эта же ситуация повторяется и в случае когда, например, $НОД(k,m)<2$ или же $len_2(c_1)? len_2(НОД(k,m))$ т.к. экономия будет либо минимальной либо будет отсутствовать в принципе.

Что делать…


для того, чтобы повысить вероятность успеха при таком способе кодирования?
В общем-то если внимательно посмотреть на ключ, то видно, что он неплохо делится на простые числа $2,3,5,7,11,17,19$, что сделано специально для успешности операции нахождения $НОД(k,m)$. Так как такая операция негативно может повлиять на количество используемых ключей, то определяя порядок следования простых множителей и сделав его частью ключевой информации, получим, хоть и не радикальное, но увеличение количества вариантов кодирования, что положительным образом отразиться на количестве ключей. Использовав вместо ключа не число $[746 130]$, а пару $[746 130, 0125763]$, где второе число отражает порядок перемножения и определяет значение $c_1$.


Следующая проблема, которую предстоит эффективно решить – соотношение частот появления простых чисел и степеней двойки, -легко заметить, что эффективность кодирования степенями двойки довольно быстро падает с ростом длины $c_1$ (см. график соответствующих последовательностей если есть один общий простой делитель) и зависит в основном от количества делителей ключа и их значений.


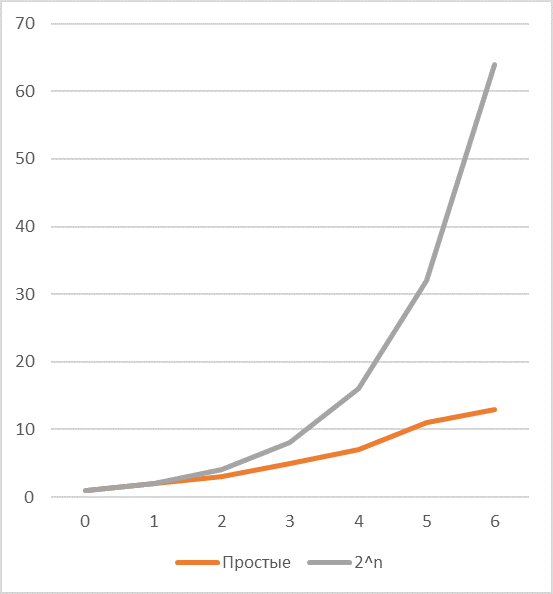
image

В случае если, общих делителей два и один из них, например, равен $3$, то возможности по экономии возрастают весьма заметно.

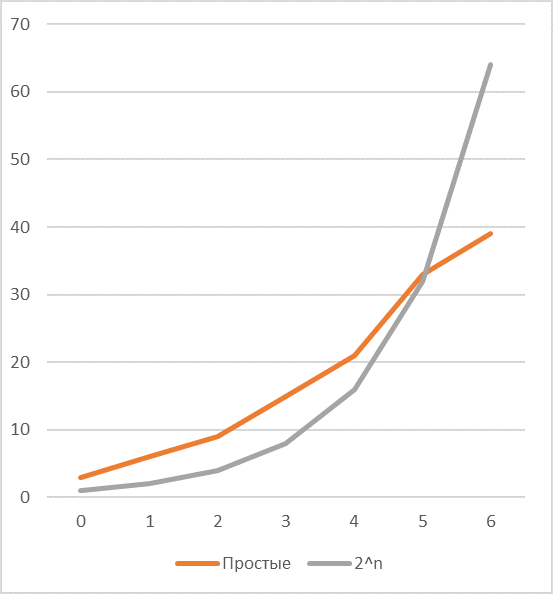
image

Что означает, что для эффективного кодирования необходимо придумать более эффективный способ кодирования $c_1$.

То есть тему есть смысл прокапывать дальше.


Пример


Как обычно выложены на github [5] – используется Excel т.к. он есть у многоих и нет необходимости думать о совместимости. В файле две закладки:


  • «Тест» — сами вычисления и т.к. в них довольно активно используется функция Excel «СЛУЧМЕЖДУ()» и числа ключа и сообщения могут оказаться взаимно простые, то придётся несколько раз встать в какую либо ячейку и нажать enter для того, чтобы получить искомую экономию (результаты в строчках 31-36);
  • «Пример 1» – приведены примеры готовых вычислений, т.к. случайность в excel не оставляет им шанса на повторение.

Ссылки


  1. Сингх Саймон. Книга шифров. Тайная история шифров и их расшифровки. М. Астрель 2007.
  2. https://ru.wikipedia.org/wiki/%D0%98%D0%BD%D1%84%D0%BE%D1%80%D0%BC%D0%B0%D1%86%D0%B8%D0%BE%D0%BD%D0%BD%D0%B0%D1%8F_%D1%8D%D0%BD%D1%82%D1%80%D0%BE%D0%BF%D0%B8%D1%8F
  3. http://www.gaelic.ru/Biblioteka/Folklore/anekdoty.htm
  4. https://ru.wikipedia.org/wiki/%D0%9E%D1%81%D0%BD%D0%BE%D0%B2%D0%BD%D0%B0%D1%8F_%D1%82%D0%B5%D0%BE%D1%80%D0%B5%D0%BC%D0%B0_%D0%B0%D1%80%D0%B8%D1%84%D0%BC%D0%B5%D1%82%D0%B8%D0%BA%D0%B8
  5. https://github.com/rumiantcev/nod_code

Комментарии (23)


  1. AC130
    02.01.2018 17:39
    #10595680

    1) Поясните пожалуйста, каким именно образом вы считали кол-во информации?
    2) Откуда взялась привязка к НОД(m, k)? Почему нельзя просто взять фиксированный список простых чисел (в общем случае независящий от ключа) и отмечать единичками разложение по этому списку? С учётом того что получателю сообщение неизвестно, ему и НОД неизвестен, и большой разницы между НОД(m, k) и НОД(m, r), где r — выбранное случайно число, нет (коль вы всё равно этот НОД передаёте)
    3) Что вы предлагаете делать если в разложении m некое простое число встретится, к примеру, дважды?


    1. Rumyantsev Автор
      02.01.2018 17:49
      #10595692

      День добрый!



      • по п. 2 — тогда ключей будет уж очень мало, а НОД сам не передаётся, только информация о позиции множителей — экономия за счёт этого и возникает, когда попытался обойти такое ограничение, то получается, что на ключи надо накладывать много правил типа отсутствия повторений простых множителей т.е. чтобы не было ключа типа 36 = [2,2,3,3];
      • по п.3 это как раз и предусмотрено позиционным двоичным кодированием с_1 — учитывать этот момент, либо же как предыдущем пп. вводить доп. ограничения на ключ.


      1. eviom
        02.01.2018 19:13
        #10595756
        +1

        ru.wikipedia.org/wiki/%D0%9A%D0%BE%D0%BB%D0%B8%D1%87%D0%B5%D1%81%D1%82%D0%B2%D0%BE_%D0%B8%D0%BD%D1%84%D0%BE%D1%80%D0%BC%D0%B0%D1%86%D0%B8%D0%B8 — при условии равной вероятности появления каждого символа и отсутствии шума в канале вырождается в двоичный логарифм от длины;

        Все-таки скорее просто в длину, а не в ее двоичный логарифм.


        1. Rumyantsev Автор
          02.01.2018 19:26
          #10595774

          Вы правы — без учёта особенностей языка(частотность букв)-нет большого смысла разделять. Если получится подать получше — тогда, надеюсь, будет.


          1. eviom
            02.01.2018 19:37
            #10595776

            Тут особенности языка не причем: у Вас просто логарифм лишний для равновероятного случая.


      1. AC130
        02.01.2018 21:32
        #10595910

        • меня интересует почему при битовой длине сообщения m равной 26 бит вы считаете кол-во информации равным 13 бит. Я не пойму где именно я упускаю множитель 1/2
        • почему ключей будет мало? К примеру, можно рассмотреть в качестве списка простых множителей список [2, 3, 5, 7, 11, 17, 19], как у вас в примере. Можно считать что этот список передаётся приёмной стороне на этапе обмена ключей (если у нас модель с симметричным шифрованием) либо просто известен заранее как часть протокола (в ассиметричной схеме). Тогда замена сообщения m на пару c_0, c_1 остаётся такой же (т.е. выигрыш в битах сохраняется), а в качестве ключа можно брать любое число, не обязанное быть произведением множителей из списка
        • вот мне как раз и непонятно, как вы будете составлять c_1. К примеру, для сообщения m = 100 267 332 = 2 * 2 * 3 * 11 * 19 * 39979 Какие для него будут c_0 и c_1?


        1. eviom
          02.01.2018 22:11
          #10595954

          • Там похоже действительно потеряна 1/2, хоть это и не сцщественно.
          • Насколько я понимаю, по задумке метод рассчитан на m, заведомо имеющие большое количество различных делителей (по крайней мере для них получается хороший выигрыш). Тогда разумно наложить такое же требование на k, чтобы минимизировать c_0.
          • Одна двойка попадает в c_1, то есть 1100101 и 39979 * 2.


          1. AC130
            02.01.2018 23:04
            #10596004

            Тогда разумно наложить такое же требование на k, чтобы минимизировать c_0.

            Как будет минимизироваться c_0? Если мы не используем список множителей из ключа, а используем свой список множителей, то c_0 и c_1 не зависят от ключа, а зависят только от списка множителей.

            По остальным вопросам мне всё понятно, спасибо большое!


        1. Rumyantsev Автор
          02.01.2018 22:14
          #10595956

          • кол-во информации в одном символе при условии равновероятного появления [0,1] = 1/2*log_2(2) = 1/2 соотв. если сообщение длины n, то кол-во информации n/2;


          • меньше т.к. из перечня ключей выкидываются, например [2,2,2,3,3,5] =360 — они не привносят доп. простых множителей относительно [2,3,5] = 30, а длину с_1 увеличивают.


          • если ключ тот же — 746130, то картина такая
            Разложение на множители:
            image
            с_1 и с_2
            image
            получается если подставить в ячейки с5 и d5 в приложенном excel


          1. AC130
            02.01.2018 23:11
            #10596016

            меньше т.к. из перечня ключей выкидываются, например [2,2,2,3,3,5] =360 — они не привносят доп. простых множителей относительно [2,3,5] = 30, а длину с_1 увеличивают.

            Почему этот ключ выкидывается? Если мы не используем список множителей из ключа, а используем свой список множителей, то c_0 и c_1 не зависят от ключа, а зависят только от списка множителей.

            По остальным вопросам мне всё понятно, спасибо большое!


            1. Rumyantsev Автор
              03.01.2018 00:12
              #10596134

              Не то, чтобы выкидывается — просто если сопоставлять его простые делители [2,2,2,3,3,5] и то чем это может кодироваться [1,2,4,8,16,32,64], то не очень выгодно в разрядах получается. Т.е. выгодно, только если НОД(k,m) будет больше 64 иначе ни одного разряда сэкономить не получится.


          1. Deosis
            03.01.2018 09:44
            #10596444

            кол-во информации в одном символе при условии равновероятного появления [0,1] = 1/2*log_2(2) = 1/2 соотв. если сообщение длины n, то кол-во информации n/2;

            То есть в однобитном сообщении содержится полбита информации?


            1. Rumyantsev Автор
              03.01.2018 10:47
              #10596514

              Не совсем так — то, что написал касалось сообщений длины n, где надо учитывать вероятность появления каждого символа, для сообщений длины 1 лучше говорить о собственной информации ссылка т.к. там всё детерминировано.


  1. Zolg
    02.01.2018 18:16
    #10595710

    Не пытаетесь ли вы изобрести велосипед сжатие с использованием словаря ?


    1. Rumyantsev Автор
      02.01.2018 19:23
      #10595770

      Нет, скорее подмечаю как найти и использовать общую часть у двух ну почти случайных чисел.


  1. eviom
    02.01.2018 19:58
    #10595810

    На самом деле не совсем корректно рассматривать сжатие, не фиксировав (нетривиальное) вероятностное пространство над сообщениями, ведь без этого мы никак не сможем сравнивать алгоритмы сжатия. Конечно можно сказать, что все сообщения заданной длины равновероятны, но тогда мы принципиально не сможем ничего сжать.


    1. Rumyantsev Автор
      02.01.2018 20:55
      #10595864

      Если начинать сравнивать, то да. Просто хотелось сначала показать, что в самом сложном случае, когда берутся два почти случайные числа, можно, найдя общую информацию её не передавать. А так как Вы верно заметили, что реальные сообщения не случайны, то дальше хочется заняться уже переложением этой темы на практику.


      1. Zolg
        02.01.2018 23:14
        #10596022

        можно, найдя общую информацию

        объявить ее словарем (имеющимся у обоих сторон) и


        её не передавать

        заменив на ссылки на словарь


        Остальная часть повествования, извините, танцы с бубном и наведение тени на плетень.


        1. Rumyantsev Автор
          03.01.2018 00:20
          #10596144

          Да и не претендую я на словарное кодирование — давно изобрели
          Так, то сама идея-то простая: т.к. ключ тоже содержит информацию, то давайте ей воспользуемся, чтобы не передавать её, а дальше НОД — только способ излечения общей части достаточно универсальный, чтобы не сильно думать о словаре.


  1. Ingref
    03.01.2018 10:03
    #10596452

    Возможен ли такой вариант?

    Простые делители ключа k: 2,3,5,11,19
    Простые делители сообщения m: 2,3,11,19, 39 979
    НОД(k,m): 2,3,11,19

    Двоичная запись общих делителей: 1,1,0,1,1

    Простые делители ключа k: 2,3,7,11,19
    Простые делители сообщения m: 2,3,11,19, 39 979
    НОД(k,m): 2,3,11,19

    Двоичная запись общих делителей: 1,1,0,1,1

    То есть, при разных комбинациях простых делителей передаваемая двоичная часть получается одинаковой и восстановить сообщение невозможно. Или я ошибаюсь и такого не может быть?


    1. Rumyantsev Автор
      03.01.2018 11:01
      #10596542

      Передаваемая часть действительно будет одинаковой, в обоих случаях
      image
      Но т.к. ключ известен двум сторонам, то восстановить полученную информацию можно полностью т.к получив 11011 мы в обоих случаях восстанавливаем НОД(k,m)=1254 =[2,3,11,19].


      Другое дело, что если ключ долго не менять, то поигравшись сообщениями (мы-то знаем делители сообщения) и понаблюдав за каналом, его можно и восстановить.


      1. Ingref
        03.01.2018 18:11
        #10597262

        Спасибо, теперь понял! Интересный алгоритм получается. В теории, если в качестве ключа взять очень большой объём разнообразной информации, то экономия будет всё больше и больше. Остаётся только найти грань, за которой ресурсы, затрачиваемые на обработку большого ключа, оправдывают экономию при передаче информации.

        И, я так понимаю, отличие от алгоритма со словарём в том, что не нужно тратить время и ресурсы на составление словаря. Но зато надо их тратить на выделение информации из ключа.


        1. Rumyantsev Автор
          03.01.2018 18:19
          #10597280

          Вы правы. Но есть надежда на то, что поиск простых делителей довольно отработанный хоть и не очень быстрый алгоритм — делим на всё подряд до корня из числа с оценкой O(n^{0.5})