Многие задачи на алгоритмы требуют знания определённых структур данных. Стек, очередь, куча, динамический массив, двоичное дерево поиска — нечасто решение алгоритмической задачи обходится без использования чего-либо из них. Однако, качественная их реализация — нетривиальная задача, и при написании кода всегда хочется по максимуму обойтись использованием стандартной библиотеки языка.
Что касается Python, то в нём есть почти всё.
Но вот самобалансирующегося дерева поиска, как такового, в стандартной библиотеке нет. А жаль!
В этой статье я разберу несколько алгоритмических задачек, подразумевающих решение с помощью двоичного дерева, и покажу, чем в разных ситуациях его можно заменить в Питоне.
Вы наверняка и так знаете, что самобалансирующееся двоичное дерево поиска — удобнейшая структура данных для многих задач, поддерживающая множество операций. Но я на всякий случай перечислю их и напомню их асимптотическую сложность.
И многое другое (наверное). В общем, иметь под рукой дерево очень и очень удобно. Что ж, перейдём к задачам!
На прямой стоят небоскрёбы, некоторые из которых перекрывают друг друга. Нужно описать очертания на фоне неба всей совокупности небоскрёбов.

Здания описаны как массив кортежей вида (координата левого края здания, координата правого края здания, высота). На выход нужно передать массив кортежей (x, y), описывающих общий силуэт зданий.
Эта задача решается за . Алгоритм в целом примерно такой: сортируем все точки (и левые, и правые края зданий), идём по ним слева направо. Если наткнулись на левый край здания — надо добавить его в перечень активных на данный момент, если на правый — исключить из перечня. В любом случае каждый раз надо проверять, изменилась ли максимальная высота активных зданий, и если изменилась, записывать в ответ очередную точку. (Более подробный разбор этой задачи можно найти здесь.)
Перечень активных зданий, как структура данных, должен поддерживать быстрое добавление нового элемента, удаление произвольного элемента и нахождение максимума. Двоичное дерево умеет делать все три операции за и идеально подходит для этой задачи. Попробуем обойтись без него!
Необходимость быстро брать максимум, конечно, напоминает нам о куче. Но куча не предусматривает удаления произвольного элемента! Например, чтобы удалить элемент кучи с известным индексом в Python за приемлемое время, нужно залезть в нестандартизированные детали реализации модуля
(Этот код взят из ответа на StackOverflow.)
Однако, есть возможность сделать надстройку над кучей, позволяющую удалять произвольный элемент за амортизированное . Алгоритм такой:
Остаётся только учесть, что элементы могут повторяться.
Код:
Эта задача встречается в разных вариантах. Наиболее общо с учётом специфики Питона можно сформулировать так: на вход алгоритму подаётся итератор неизвестной (и, возможно, неограниченной) длины. Нужно вернуть итератор с медианами по всем окнам заранее заданной ширины .
При оптимальном решении этой задачи каждая следующая медиана вычисляется за амортизированное . Как и большинстве задач на скользящее окно, решение заключается в построении структуры данных, позволяющей быстро добавлять в окно новый элемент, удалять самый старый и вычислять очередную медиану.
Дерево, очевидно, решает эту задачу. Добавление, удаление и нахождение медианы за дают оптимальную асимптотику для нашего варианта постановки задачи. Существует также способ уменьшить сложность нахождения медианы до амортизированного : для этого надо помнить указатель на медианный элемент (или два элемента, среднее арифметическое которых даёт медиану, если чётное) и обновлять его при добавлении и удалении элементов (обновление будет стоить амортизированное — подумайте, почему!).
Если подумать, элементы, нужные для нахождения медианы, в дереве могут лежать только в трёх местах:
Слова «наменьший» и «наибольший», конечно же, снова напоминают нам о кучах!
Действительно, давайте хранить две кучи, min-кучу и max-кучу, сбалансированного размера. При этом все элементы max-кучи должны быть меньше всех элементов min-кучи. При добавлении элемента нужно положить его в правильную кучу и сбалансировать их: это потребует конечного числа операций вида «извлеки экстремальное значение из одной кучи и положи в другую», стоящих . Получение медианы стоит , так как для этого нужен только максимум max-кучи и минимум min-кучи.
Код:
(Для этого кода я добавил в
Решение задачи с такой структурой данных становится элементарным:
Дан массив чисел Нужно вычислить количество пар элементов массива, которые стоят в неправильном порядке, то есть при имеет место Если массив состоит из разных чисел от 1 до n, то чётность этого количества есть не что иное, как чётность перестановки, описываемой этим массивом.
Задача также обобщается на случай, когда плохими парами объявляются те, для которых и , где — некоторый положительный коэффициент.
В обоих случаях она решается за памяти и времени (кроме случая перестановки, в котором она решается за — но это уже совсем другая история). Элементарное решение с деревом выглядит примерно так: идём по массиву, на каждом шаге прибавляем к ответу количество элементов больше текущего (или текущего, умноженного на ?) — дерево делает это за — и после этого добавляем в дерево текущий элемент.
Здесь уже одними кучами не обойтись!
Но и без дерева не обойтись тоже. Реализовать дерево несложно; но если его не балансировать, то в худшем случае асимптотика ухудшится до ! Что же делать?
Развернём задачу и пойдём с другого конца. Ведь можно сначала построить всё дерево целиком, на каждом шаге цикла удалять из него текущий элемент и прибавлять к ответу количество элементов меньше текущего. Построить сбалансированное дерево легко — достаточно изначально отсортировать массив и написать грамотную рекурсию:
А вот удаление из дерева — занятие муторное. Неудачный алгоритм удаления может испортить дерево и снова сделать его неприемлемой высоты! Поэтому давайте будем не удалять узлы из дерева, а лишь помечать их как удалённые. Тогда с высотой дерева за всё время работы алгоритма гарантированно ничего не произойдёт и мы получим вожделенное .
Правда, при таком подходе наличие узлов с повторяющимися элементами (особенно в большом количестве) может сильно испортить жизнь. Поэтому имеет смысл перед построением дерева произвести дедупликацию элементов с подсчётом кратности.
Код:
Решение задачи, соответственно, снова элементарное:
Эта задача вообще не требует самобалансирующихся деревьев — привожу её в качестве бонуса, чтобы рассказать ещё чуть-чуть о деревьях в Питоне.
Есть виртуальная корзина с шарами k разных цветов. В корзину можно положить шар определённого цвета, а можно вытащить случайный шар. Задача — программно смоделировать такую корзину с максимально эффективными операциями.
Очевидное решение — операций на добавление шара и на выбор случайного: храним массив с количеством шаров каждого цвета и суммарное количество шаров N, при необходимости выбрать случайный шар генерируем случайное число от 0 до N — 1 и смотрим, куда оно попало. (Например, есть 2 шара нулевого цвета, 1 шар первого цвета и 4 шара второго. Если выпало 0 или 1, выбрался шар нулевого цвета; если 2, то первого цвета; если 3, 4, 5 или 6 — второго цвета.)
Однако можно организовать корзину так, чтобы обе операции стоили . Для этого количество шаров каждого цвета нужно хранить в листьях дерева, а в остальных узлах — суммы по всем листьям в соответствующих поддеревьях.
Поскольку k задано, мы заранее знаем, сколько в дереве будет листьев. Количество узлов тоже не может измениться. Итого мы имеем дерево константного размера; когда мы попробуем этот размер вычислить, мы заметим, что у него есть ещё одно особенное свойство.
Предположим, что мы знаем, сколько нам нужно узлов. Попробуем уложить всё дерево в массив, как это делает Питон в модуле
У каждого узла есть свой индекс в массиве. У корня этот индекс — 0, у детей узла с индексом
Нам нужно, чтобы в дереве было определённое число листьев. Легко, когда это число — степень двойки. Листья в этом случае просто занимают целый слой дерева и в памяти располагаются подряд.
Но что, если k между двумя степенями двойки? Что ж, мы можем раскрыть несколько бутонов (обязательно с левого края!), чтобы число листьев стало таким, как нам надо:
Заметим, что при этом все листья по-прежнему расположены в памяти подряд! Это полезное свойство очень поможет нам при реализации.
Остаётся лишь вычислить, сколько нужно узлов для дерева с заданным количеством листьев k. Когда k — степень двойки, всё понятно: всего в дереве будет узлов. Удивительно, но и во всех остальных случаях тоже!
Код:
Да, большинство этих задач имеют решения вообще без деревьев. Тем не менее я считаю, что попробовать решить их так было полезным упражнением. Надеюсь, и для вас тоже! Спасибо за внимание.
Что касается Python, то в нём есть почти всё.
- Динамический массив — встроенный тип
list. Он же поддерживает и стековые операции:.append()и.pop(). - Хэш-таблица — встроенные типы
setиdict, а также неизменяемый брат сетаfrozenset. - Куча —
listсо специальными операциями вставки и удаления, реализованными в модулеheapq. - Двусторонняя очередь — это описанный в модуле
collectionsтипdeque.
Но вот самобалансирующегося дерева поиска, как такового, в стандартной библиотеке нет. А жаль!
В этой статье я разберу несколько алгоритмических задачек, подразумевающих решение с помощью двоичного дерева, и покажу, чем в разных ситуациях его можно заменить в Питоне.
На что способно дерево поиска
Вы наверняка и так знаете, что самобалансирующееся двоичное дерево поиска — удобнейшая структура данных для многих задач, поддерживающая множество операций. Но я на всякий случай перечислю их и напомню их асимптотическую сложность.
- Вставка элемента — стоит
- Удаление элемента — стоит
- Поиск элемента — стоит
- Нахождение минимального и максимального элементов — стоит . При особой необходимости можно помнить указатели на них; тогда потребность в проходе по дереву отпадает и стоимость снижается до
- Нахождение медианы, да и вообще любой k-й порядковой статистики — стоит При этом придётся в каждом узле дерева помнить размер соответствующего поддерева.
- Нахождение количества элементов меньше/больше заданного — стоит Для этого тоже необходимо в каждом узле дерева помнить размер соответствующего поддерева.
- Вставка монотонной последовательности элементов — может стоить амортизированное на каждый! (Знаете ли вы, что в C++
std::setможно наполнить из сортированного массива за ?)
И многое другое (наверное). В общем, иметь под рукой дерево очень и очень удобно. Что ж, перейдём к задачам!
Задача: небоскрёбы
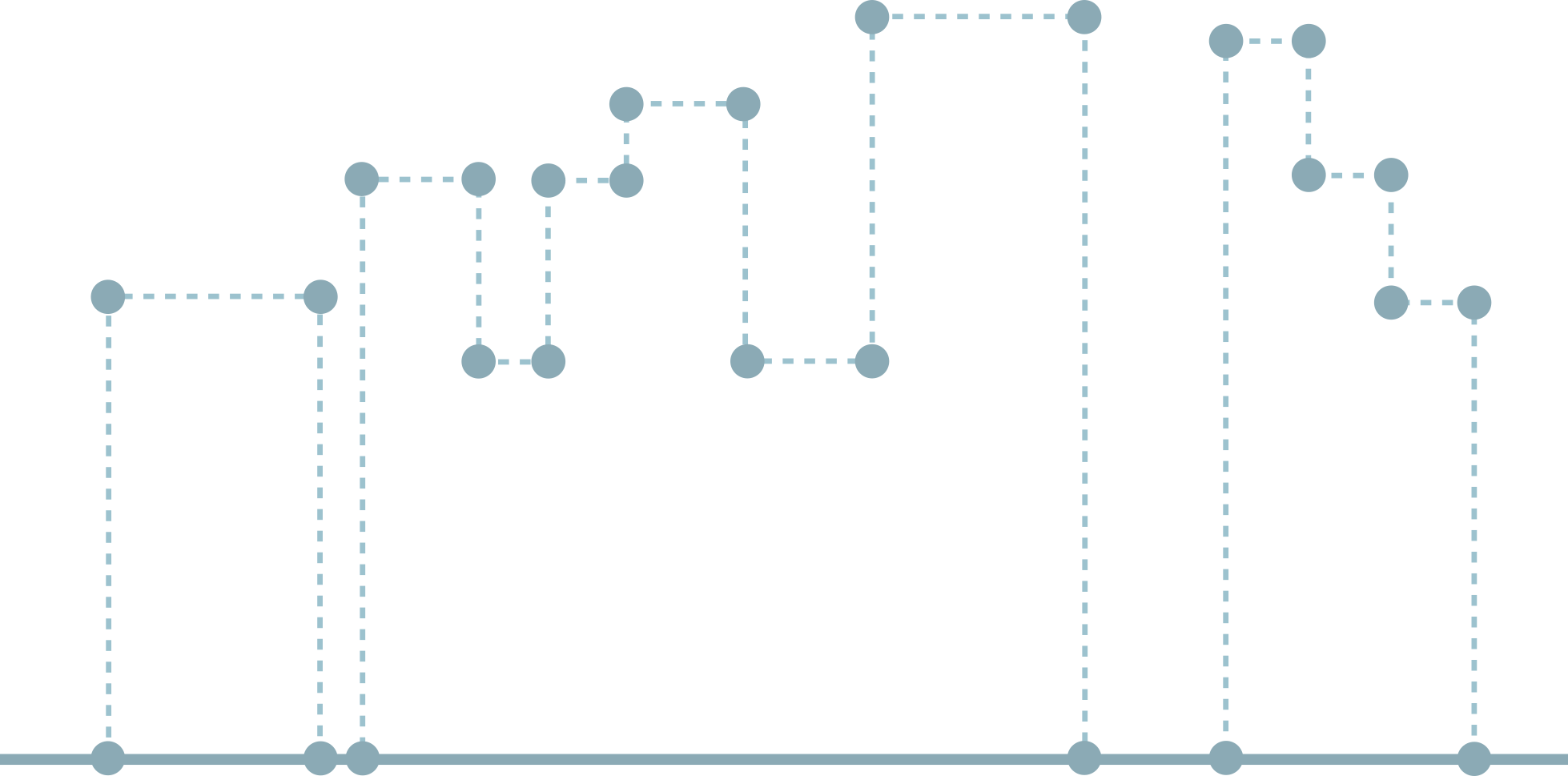
На прямой стоят небоскрёбы, некоторые из которых перекрывают друг друга. Нужно описать очертания на фоне неба всей совокупности небоскрёбов.


Здания описаны как массив кортежей вида (координата левого края здания, координата правого края здания, высота). На выход нужно передать массив кортежей (x, y), описывающих общий силуэт зданий.
Эта задача решается за . Алгоритм в целом примерно такой: сортируем все точки (и левые, и правые края зданий), идём по ним слева направо. Если наткнулись на левый край здания — надо добавить его в перечень активных на данный момент, если на правый — исключить из перечня. В любом случае каждый раз надо проверять, изменилась ли максимальная высота активных зданий, и если изменилась, записывать в ответ очередную точку. (Более подробный разбор этой задачи можно найти здесь.)
Перечень активных зданий, как структура данных, должен поддерживать быстрое добавление нового элемента, удаление произвольного элемента и нахождение максимума. Двоичное дерево умеет делать все три операции за и идеально подходит для этой задачи. Попробуем обойтись без него!
Необходимость быстро брать максимум, конечно, напоминает нам о куче. Но куча не предусматривает удаления произвольного элемента! Например, чтобы удалить элемент кучи с известным индексом в Python за приемлемое время, нужно залезть в нестандартизированные детали реализации модуля
heapq (что, конечно, ненадёжно и не рекомендуется):def heapremove(h, i):
h[i] = h[-1]
h.pop()
if i < len(h):
heapq._siftup(h, i)
heapq._siftdown(h, 0, i)(Этот код взят из ответа на StackOverflow.)
Однако, есть возможность сделать надстройку над кучей, позволяющую удалять произвольный элемент за амортизированное . Алгоритм такой:
- Храним вместе с кучей множество удалённых элементов.
- Если требуется удалить элемент, не являющийся сейчас минимальным в куче, добавляем его в множество удалённых элементов.
- Если требуется удалить элемент, являющийся сейчас минимальным, удаляем его стандартным
heappop. Если новый минимальным элемент содержится в множестве удалённых элементов, удаляем и его, и так далее.
Остаётся только учесть, что элементы могут повторяться.
Код:
class HeapWithRemoval(object):
def __init__(self):
self.heap = []
# Делаем не set, а словарь со счётчиком на случай повторов
self.deleted = collections.defaultdict(int)
def add(self, value):
if self.deleted[value]:
self.deleted[value] -= 1
else:
heapq.heappush(self.heap, value)
def remove(self, value):
self.deleted[value] += 1
while self.heap and self.deleted[self.heap[0]]:
self.deleted[self.heap[0]] -= 1
heapq.heappop(self.heap)
def minimum(self):
return self.heap[0] if self.heap else NoneЗадача: медиана в скользящем окне
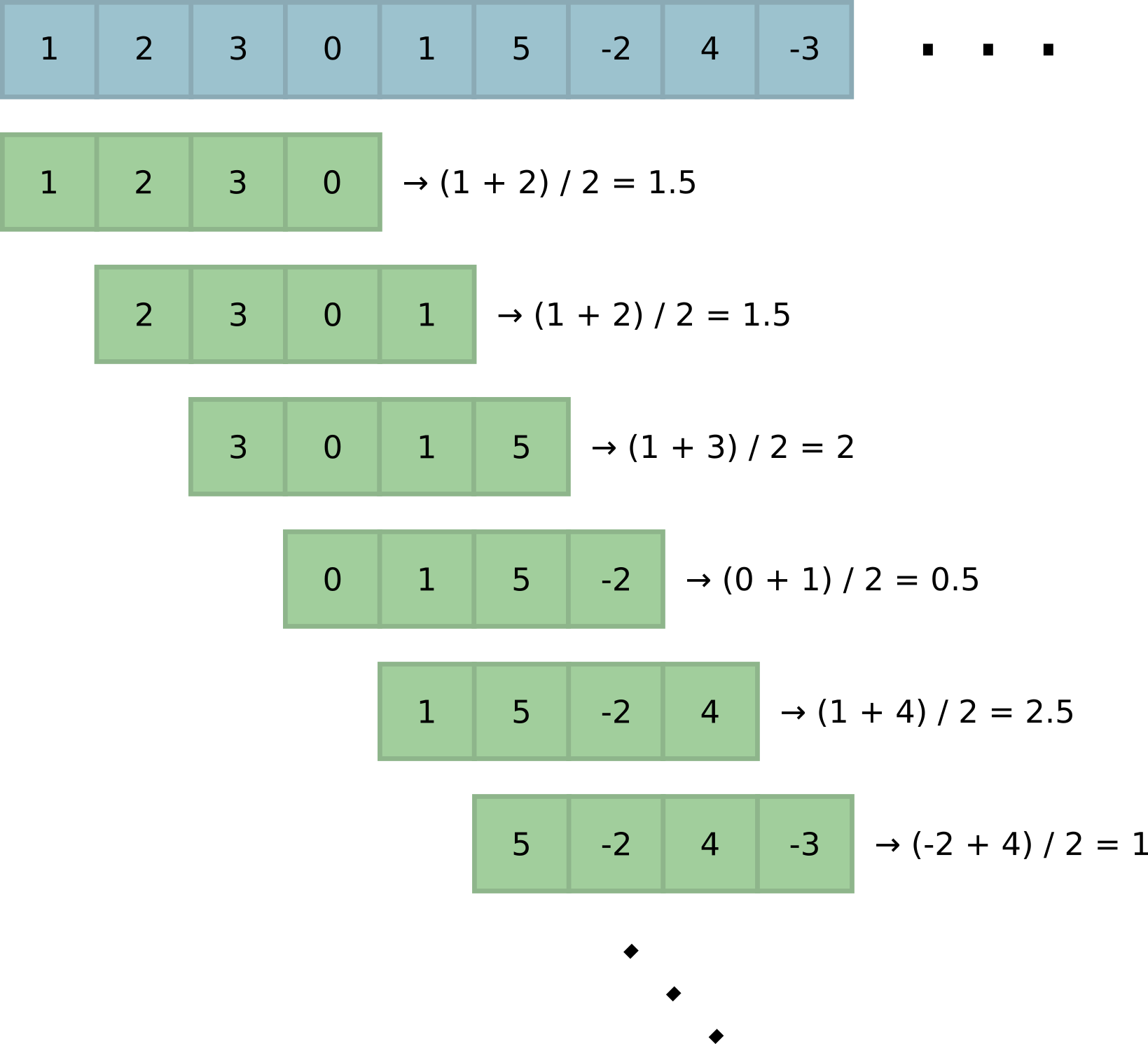
Эта задача встречается в разных вариантах. Наиболее общо с учётом специфики Питона можно сформулировать так: на вход алгоритму подаётся итератор неизвестной (и, возможно, неограниченной) длины. Нужно вернуть итератор с медианами по всем окнам заранее заданной ширины .

При оптимальном решении этой задачи каждая следующая медиана вычисляется за амортизированное . Как и большинстве задач на скользящее окно, решение заключается в построении структуры данных, позволяющей быстро добавлять в окно новый элемент, удалять самый старый и вычислять очередную медиану.
Дерево, очевидно, решает эту задачу. Добавление, удаление и нахождение медианы за дают оптимальную асимптотику для нашего варианта постановки задачи. Существует также способ уменьшить сложность нахождения медианы до амортизированного : для этого надо помнить указатель на медианный элемент (или два элемента, среднее арифметическое которых даёт медиану, если чётное) и обновлять его при добавлении и удалении элементов (обновление будет стоить амортизированное — подумайте, почему!).
Если подумать, элементы, нужные для нахождения медианы, в дереве могут лежать только в трёх местах:
- в корне;
- в наименьшем элементе правого поддерева;
- в наибольшем элементе левого поддерева.
Слова «наменьший» и «наибольший», конечно же, снова напоминают нам о кучах!
Действительно, давайте хранить две кучи, min-кучу и max-кучу, сбалансированного размера. При этом все элементы max-кучи должны быть меньше всех элементов min-кучи. При добавлении элемента нужно положить его в правильную кучу и сбалансировать их: это потребует конечного числа операций вида «извлеки экстремальное значение из одной кучи и положи в другую», стоящих . Получение медианы стоит , так как для этого нужен только максимум max-кучи и минимум min-кучи.
Код:
class MedianFinder(object):
def __init__(self, k):
self.k = k
self.smaller_heap = HeapWithRemoval()
self.larger_heap = HeapWithRemoval()
# Нам нужно помнить порядок прибытия элементов, чтобы удалять старые:
self.elements = deque([], k)
def add(self, num):
if len(self.elements) == self.k:
# Элементов слишком много - время удалить старый из соотв. кучи.
element_to_delete = self.elements[0]
if self.smaller_heap and element_to_delete <= -self.smaller_heap.minimum():
self.smaller_heap.remove(-element_to_delete)
else:
self.larger_heap.remove(element_to_delete)
self.balance()
# Добавляем новый элемент в нужную кучу.
if self.larger_heap and num >= self.larger_heap.minimum():
self.larger_heap.add(num)
else:
self.smaller_heap.add(-num)
self.elements.append(num)
self.balance()
def balance(self):
# Алгоритм построен так, что одна куча не может стать сильно больше другой.
if len(self.larger_heap) > len(self.smaller_heap) + 1:
num = self.larger_heap.pop()
self.smaller_heap.add(-num)
elif len(self.smaller_heap) > len(self.larger_heap) + 1:
num = -self.smaller_heap.pop()
self.larger_heap.add(num)
def median(self):
if len(self.larger_heap) > len(self.smaller_heap):
return self.larger_heap.minimum()
if len(self.larger_heap) < len(self.smaller_heap):
return -self.smaller_heap.minimum()
return (self.larger_heap.minimum() - self.smaller_heap.minimum()) / 2(Для этого кода я добавил в
HeapWithRemoval методы pop,__len__ и __nonzero__.)Решение задачи с такой структурой данных становится элементарным:
def median_over_sliding_window(input, k):
finder = MedianFinder(k)
for num in input:
finder.add(num)
if len(finder.elements) == k:
yield finder.median()Задача: количество инверсий
Дан массив чисел Нужно вычислить количество пар элементов массива, которые стоят в неправильном порядке, то есть при имеет место Если массив состоит из разных чисел от 1 до n, то чётность этого количества есть не что иное, как чётность перестановки, описываемой этим массивом.
Задача также обобщается на случай, когда плохими парами объявляются те, для которых и , где — некоторый положительный коэффициент.
В обоих случаях она решается за памяти и времени (кроме случая перестановки, в котором она решается за — но это уже совсем другая история). Элементарное решение с деревом выглядит примерно так: идём по массиву, на каждом шаге прибавляем к ответу количество элементов больше текущего (или текущего, умноженного на ?) — дерево делает это за — и после этого добавляем в дерево текущий элемент.
Здесь уже одними кучами не обойтись!
Но и без дерева не обойтись тоже. Реализовать дерево несложно; но если его не балансировать, то в худшем случае асимптотика ухудшится до ! Что же делать?
Развернём задачу и пойдём с другого конца. Ведь можно сначала построить всё дерево целиком, на каждом шаге цикла удалять из него текущий элемент и прибавлять к ответу количество элементов меньше текущего. Построить сбалансированное дерево легко — достаточно изначально отсортировать массив и написать грамотную рекурсию:
import collections
Node = collections.namedtuple("Node", "value left right")
def make_tree(nums):
nums = sorted(nums)
return _make_tree(nums, 0, len(nums))
def _make_tree(nums, l, r):
# На вход получаем отсортированный массив элементов.
# Конвертируем в дерево подмассив с индексами в [l, r).
if r - l <= 0:
return None
if r - l == 1:
return Node(nums[l], None, None)
center = (l + r) // 2
left_subtree = _make_tree(nums, l, center)
right_subtree = _make_tree(nums, center + 1, r)
return Node(nums[center], left_subtree, right_subtree)А вот удаление из дерева — занятие муторное. Неудачный алгоритм удаления может испортить дерево и снова сделать его неприемлемой высоты! Поэтому давайте будем не удалять узлы из дерева, а лишь помечать их как удалённые. Тогда с высотой дерева за всё время работы алгоритма гарантированно ничего не произойдёт и мы получим вожделенное .
Правда, при таком подходе наличие узлов с повторяющимися элементами (особенно в большом количестве) может сильно испортить жизнь. Поэтому имеет смысл перед построением дерева произвести дедупликацию элементов с подсчётом кратности.
Код:
import collections
class Node(object):
def __init__(self, value, smaller, larger, total_count):
self.smaller = smaller # левое поддерево
self.larger = larger # правое поддерево
self.value = value
self.total_count = total_count # общее число узлов в этом поддереве
def count_smaller(self, value):
if not self.total_count:
# Чего тянуть резину?
return 0
if value <= self.value:
return self.smaller.count_smaller(value) if self.smaller else 0
if self.larger:
larger = self.larger.total_count - self.larger.count_smaller(value)
return self.total_count - larger
return self.total_count
def remove(self, value):
# Нерекурсивная версия. Потому что я могу.
while True:
self.total_count -= 1
if value == self.value:
return
self = self.smaller if value < self.value else self.larger
def make_tree(nums):
nums = sorted(nums)
counter = collections.Counter(nums)
return _make_tree(nums, counter, 0, len(nums))
def _make_tree(nums, counter, l, r):
# На вход получаем отсортированный массив элементов и словарь с их
# кратностями. Конвертируем в дерево подмассив с индексами в [l, r).
if r - l <= 0:
return None
if r - l == 1:
return Node(nums[l], None, None, counter[nums[l]])
center = (l + r) // 2
left_subtree = _make_tree(nums, counter, l, center)
right_subtree = _make_tree(nums, counter, center + 1, r)
value = nums[center]
# Не стоит забывать, что нам нужен учёт количества элементов в поддеревьях.
total_count = counter[value] + (left_subtree.total_count if left_subtree else 0) + (right_subtree.total_count if right_subtree else 0)
return Node(value, left_subtree, right_subtree, total_count)Решение задачи, соответственно, снова элементарное:
def count_inversions(nums, coef=1.0):
tree = make_tree(nums)
result = 0
for num in nums:
tree.remove(num)
result += tree.count_smaller(num * coef)
return resultБонусная задача: корзина с шарами
Эта задача вообще не требует самобалансирующихся деревьев — привожу её в качестве бонуса, чтобы рассказать ещё чуть-чуть о деревьях в Питоне.
Есть виртуальная корзина с шарами k разных цветов. В корзину можно положить шар определённого цвета, а можно вытащить случайный шар. Задача — программно смоделировать такую корзину с максимально эффективными операциями.
Очевидное решение — операций на добавление шара и на выбор случайного: храним массив с количеством шаров каждого цвета и суммарное количество шаров N, при необходимости выбрать случайный шар генерируем случайное число от 0 до N — 1 и смотрим, куда оно попало. (Например, есть 2 шара нулевого цвета, 1 шар первого цвета и 4 шара второго. Если выпало 0 или 1, выбрался шар нулевого цвета; если 2, то первого цвета; если 3, 4, 5 или 6 — второго цвета.)
Однако можно организовать корзину так, чтобы обе операции стоили . Для этого количество шаров каждого цвета нужно хранить в листьях дерева, а в остальных узлах — суммы по всем листьям в соответствующих поддеревьях.
Поскольку k задано, мы заранее знаем, сколько в дереве будет листьев. Количество узлов тоже не может измениться. Итого мы имеем дерево константного размера; когда мы попробуем этот размер вычислить, мы заметим, что у него есть ещё одно особенное свойство.
Предположим, что мы знаем, сколько нам нужно узлов. Попробуем уложить всё дерево в массив, как это делает Питон в модуле
heapq:
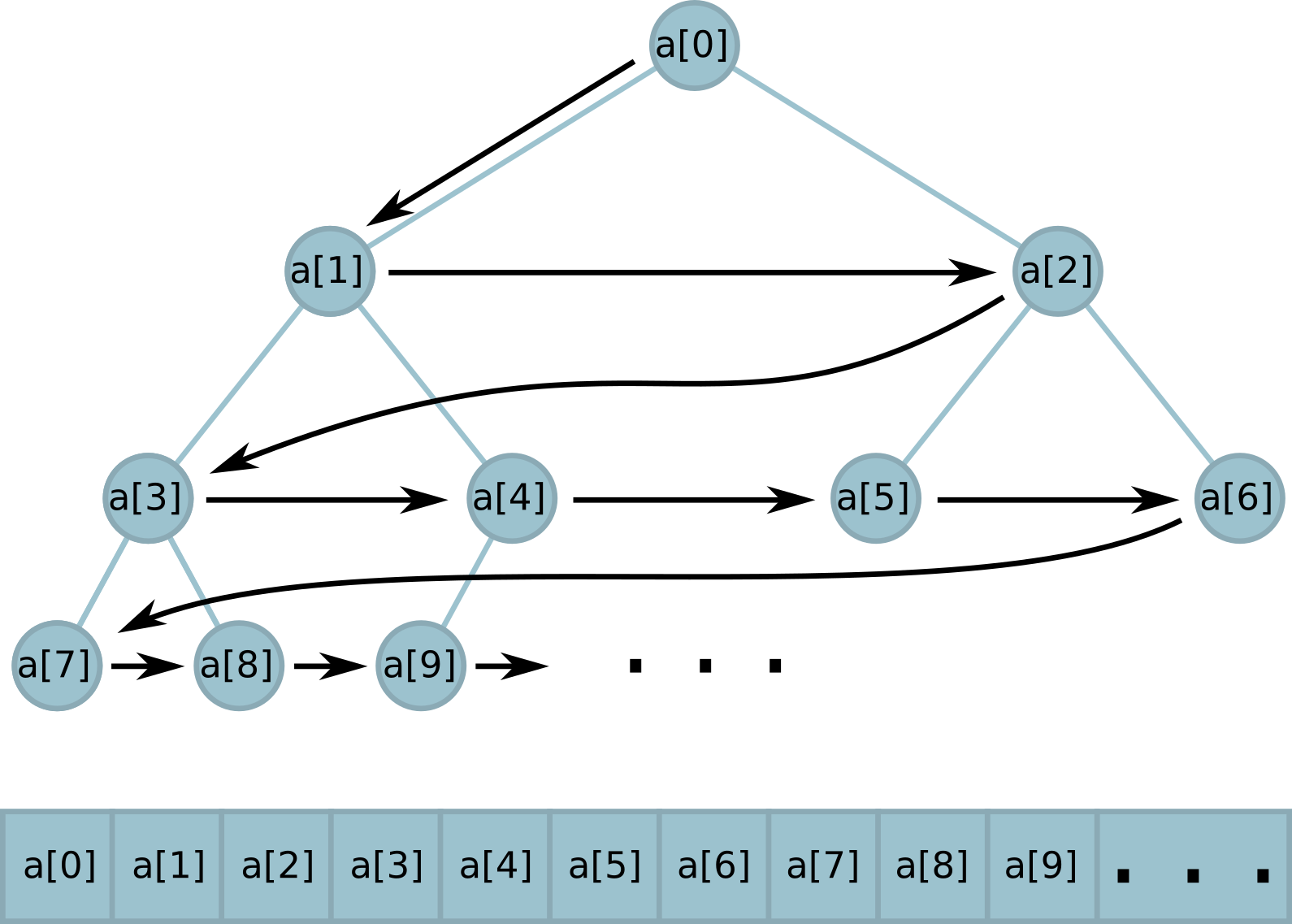
У каждого узла есть свой индекс в массиве. У корня этот индекс — 0, у детей узла с индексом
i — индексы (2 * i + 1) у левого и (2 * i + 2) у правого; у родителя узла с индексом i индекс (i - 1) // 2.Нам нужно, чтобы в дереве было определённое число листьев. Легко, когда это число — степень двойки. Листья в этом случае просто занимают целый слой дерева и в памяти располагаются подряд.

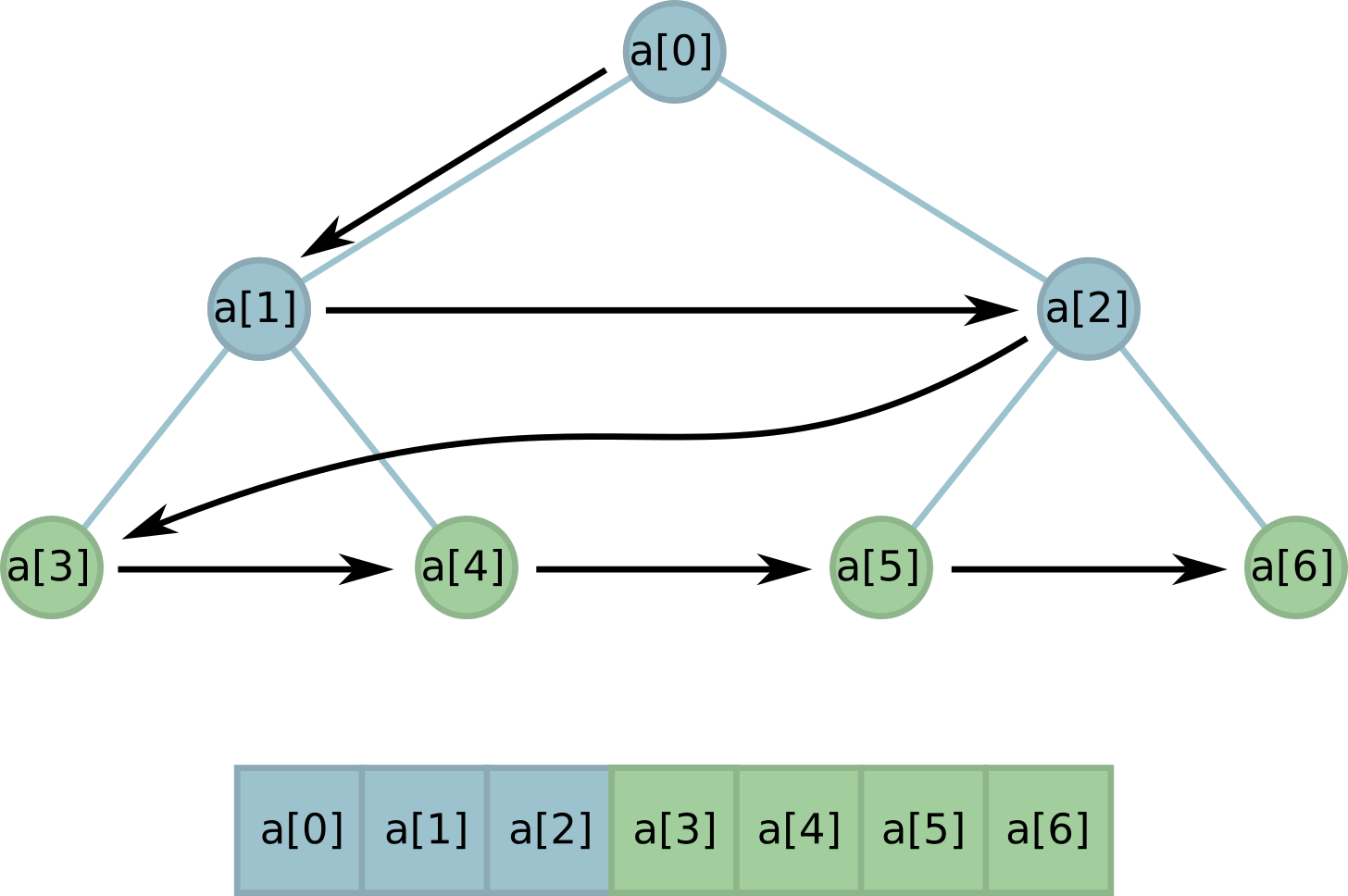
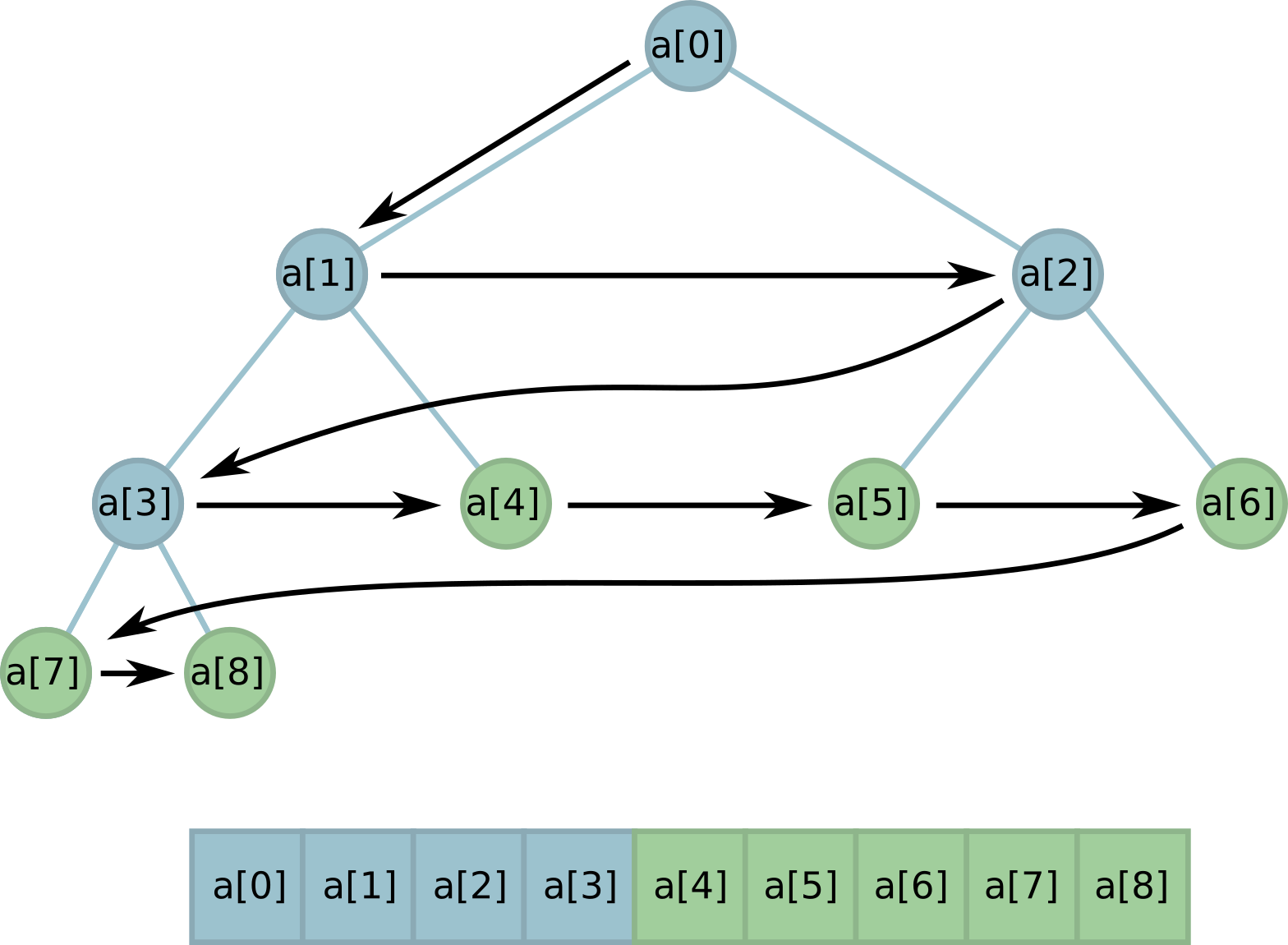
Но что, если k между двумя степенями двойки? Что ж, мы можем раскрыть несколько бутонов (обязательно с левого края!), чтобы число листьев стало таким, как нам надо:

Заметим, что при этом все листья по-прежнему расположены в памяти подряд! Это полезное свойство очень поможет нам при реализации.
Остаётся лишь вычислить, сколько нужно узлов для дерева с заданным количеством листьев k. Когда k — степень двойки, всё понятно: всего в дереве будет узлов. Удивительно, но и во всех остальных случаях тоже!
Доказательство
Мы ищем дерево минимальной высоты с k листьями и перекосом в сторону левого поддерева, если он необходим (то есть если k — не степень двойки).
Если , такое дерево состоит из одного (листового) узла и для него формула верна.
Если и степень двойки, формула снова верна.
Если и не степень двойки, нужно построить дерево с двумя поддеревьями, удовлетворяющими искомому свойству (и гарантированно непустыми!). Для них формула будет верна; в первом будет листьев, во втором — листьев (), и суммарно имеем число узлов
Если , такое дерево состоит из одного (листового) узла и для него формула верна.
Если и степень двойки, формула снова верна.
Если и не степень двойки, нужно построить дерево с двумя поддеревьями, удовлетворяющими искомому свойству (и гарантированно непустыми!). Для них формула будет верна; в первом будет листьев, во втором — листьев (), и суммарно имеем число узлов
Код:
import random
class Bucket(object):
def __init__(self, k):
self.k = k
# Изначально у нас ноль шаров каждого цвета,
# и все частичные суммы тоже нули.
self.tree = [0] * (2 * k - 1)
def add_ball(self, color):
# Вычислить индекс в массиве по индексу цвета легко!
node_index = self.k - 1 + color
while node_index >= 0:
# Увеличиваем количество шаров заданного цвета
# и суммы во всех предках соответствующего узла.
self.tree[node_index] += 1
node_index = (node_index - 1) // 2
def pick_ball(self):
total_balls = self.tree[0]
ball_index = random.randrange(total_balls)
node_index = 0
# Определить, дошли ли мы до листа, легко -
# индексы листьев начинаются с (k - 1).
while node_index < self.k - 1:
self.tree[node_index] -= 1
left_child_index = 2 * node_index + 1
right_child_index = 2 * node_index + 2
if ball_index < self.tree[left_child_index]:
node_index = left_child_index
else:
ball_index -= self.tree[left_child_index]
node_index = right_child_index
self.tree[node_index] -= 1
return node_index - self.k + 1P. S.
Да, большинство этих задач имеют решения вообще без деревьев. Тем не менее я считаю, что попробовать решить их так было полезным упражнением. Надеюсь, и для вас тоже! Спасибо за внимание.

