«Цель этого курса — подготовить вас к вашему техническому будущему.»

Привет, Хабр. Помните офигенную статью «Вы и ваша работа» (+219, 2394 в закладки, 377k прочтений)?

Так вот у Хэмминга (да, да, самоконтролирующиеся и самокорректирующиеся коды Хэмминга) есть целая книга, написанная по мотивам его лекций. Мы ее переводи, ведь мужик дело говорит.

Это книга не просто про ИТ, это книга про стиль мышления невероятно крутых людей. «Это не просто заряд положительного мышления; в ней описаны условия, которые увеличивают шансы сделать великую работу.»

Мы уже перевели 18 (из 30) глав. И ведем работу над изданием «в бумаге».

Глава 16. Цифровые фильтры — 3

(За перевод спасибо Пахомову Андрею, который откликнулся на мой призыв в «предыдущей главе».) Кто хочет помочь с переводом, версткой и изданием книги — пишите в личку или на почту magisterludi2016@yandex.ru

И вот теперь мы готовы рассмотреть систематический синтез нерекурсивных фильтров. Метод синтеза таких фильтров показан на рисунке 16.1 и состоит из 6 частей. Слева сверху эскиз фильтра, который вы хотели бы получить в идеальном случае. Это может быть фильтр низких частот, фильтр верхних частот, полосно-заграждающий, полосно-пропускающий фильтр, фильтр-пробка или даже диференциатор. Для всех типов фильтров, кроме диференциатора, обычно стремятся получить передаточную характеристику равную 0 или 1 на различных интервалах частот, в то время как для диференциатора стремятся получить i? в качестве передаточной характеристики, потому что производная собственной функции фильтра равна



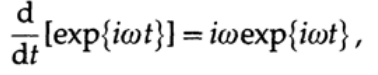
следовательно желаемые коэффициенты равняются i?.

Для диференциатора скорее всего будет задана некоторая частота среза, потому что, как вы могли заметить, дифференциирование увеличивает амплитуду сигнала, умножая ее на ?. В области высоких частот, где обычно и располагаются помехи, передаточная функция имеет наивысшие значения (рисунок 16.II). Также обратите внимание на рисунок 15.II.



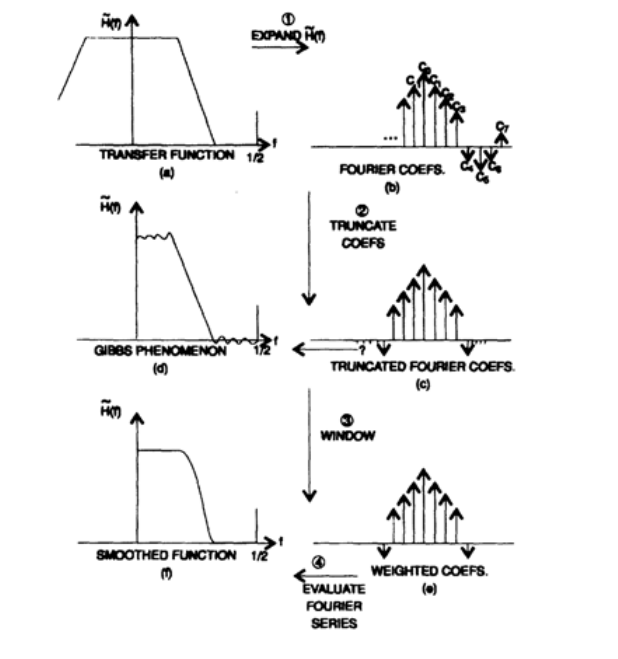
Рисунок 16.I

Коэффициенты соответствующих членов разложения в ряд Фурье легко рассчитываются, поскольку подынтегральные функции в выражении для их расчета являются простыми (когда существует производная, возможно использовать интегрирование по частям). Предположим, мы представили разложение в ряд в виде комплексных экспонент. Тогда коэффициенты фильтра — это коэффициенты соответствующих членов ряда, представленные в экспоненциальной форме. В правом верхнем углу на рисунке 16.I представлен символический график коэффициентов (конечно же, коэффициенты являются комплексными числами).

На следующем этапе (представлен ниже на рисунке 16.I) мы должны ограничить разложение в ряд 2N+1 членами (это аналогично использованию прямоугольного окна). Такое ограничение количество членов (правая часть иллюстрации) приводит к эффекту Гиббса (левая часть иллюстрации). Коэффициенты с наложенной на них оконной функций представлены в нижней правой части иллюстрации, а итоговый фильтр в нижней левой.

Метод представленный выше требует выбора количества членов ряда Фурье (N) и формы оконной функции. Если первоначальный выбор этих параметров не подходит для вашей задачи, вы выбираете другие параметры и пробуете еще раз. Это метод проб и ошибок.

Джеймс Фредерик Кайзер предложил метод синтеза, который позволяет одновременно как рассчитать количество коэффициентов ряда, так и получить конкретную оконную функцию из определенного семейства оконных функций. В этом случае необходимо задать два параметра: отклонение от идеального фильтра по вертикальной оси (?) и ширину области перехода между полосой пропускания и полосой подавления (?F), пример показан на рисунке 16.III.


Рисунок 16.III

Для полосно-пропускающего фильтра, с заданными полосой пропускания f_p и полосой подавления f_p, применяется следующая последовательность расчетов:



Если полученное значение N слишком велико, то нужно остановиться и пересмотреть дизайн фильтра, иначе вы переходите к следующему шагу:

Зависимость ?(A) представлена на графике 16.IV. Первоначальные коэффициенты разложения в ряд Фурье заданы как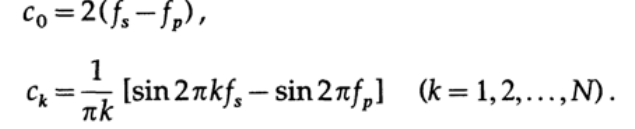



Эти коэффициенты должны быть умножены на соответствующие весовые коэффициенты w_k оконной функции



где





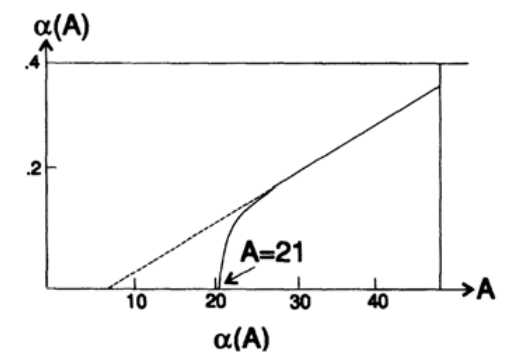
График 16.IV

I₀(x) является функцией Бесселя мнимого аргумента нулевого порядка. Для вычисления ее значения вам потребуется сравнительного немного членов, потому ряд сходится быстро благодаря квадрату n! в знаменателе.

Лучше всего вычислять значение I₀(x) рекурсивно; для заданного x следующий член ряда выражается через предыдущий как



Для фильтра низких или высоких частот одно из значений f_p или f_s has limnit possibel for it. Для частотно-заградительного фильтра формулы для расчета коэффициентов c_k немного изменяются.

Давайте исследуем коэффициенты оконной функции Кайзера, w_k:



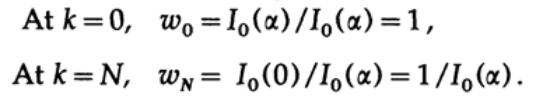
Если мы исследуем эти числа, то увидим, что для ?>0 они напоминают приподнятый косинус



а соответствующая оконная функция похожа на окна Ханна и Хэмминга. Для A>21 присутствует «платформа». Для A<21, когда ?=0, все весовые коэффициенты w_k равны единицы и мы получим окно на подобие окна Ланцоша. С увеличением A постепенно возникает платформа. Таким образом, окно Кайзера имеет те же свойства, что и многие популярные окна, но при этом конкретное окно, которое вы используете строится на основе заданных параметров, а не на основе предрассудка или догадки.

Как Кайзер вывел эти формулы? В некоторой степени методом проб и ошибок. Вначале он предположил, что у него есть один разрыв и он смоделировал много вариантов на компьютере, чтобы видеть одновременно длительность фронта ?F (Фронт сигнала — это переход сигнала из состояния 0 (нижний уровень) в 1 (верхний уровень). В данном случае имеется в виду ширина переходной полосы между полосой пропускания и полосой затухания.) и величину звона ?. После изрядного количества размышлений, прикосновения музы и не имея ничего определенного в качестве функции от A, мы заметим, что с увеличением A мы приходим от окна Ланцоша (A < 21) к платформе увеличивающейся высоты, 1/I₀(?). В идеальном случае он хотел получить вытянутую сфероидальную функцию, но он заметил, что полученные им значения точно аппроксимируются I₀(x). Он построил графики и аппроксимировал функции. Я спросил его, как он получил 0.4 для степени экспоненты. Он сказал, что он попробовал вначале 0.5, но это оказалось слишком много, тогда значение 0.4, которое к тому же отлично подошло, стало следующим логичным выбором. Это хороший пример того, что использование уже известных знания в комбинации с компьютером, в качестве инструмента для экспериментов, приводит к очень полезным результатам, даже в теоретических исследованиях.
Иногда метод Кайзера дает сбой, когда присутствует больше одного среза (на самом деле, срез отображается симметрично и на отрицательную область частот) и тогда звон, обусловленный разными срезами будет накладываться друг на друга и заложенное предельное значение звона будет превышено. В такой ситуации, которая иногда все-таки случается, следует просто повторить синтез с менее строгими ограничениями. Вся программа целиком может быть выполнена на небольшом, помещающемся в руку программируемом калькуляторе, например TI-59, не говоря уже о современном PC.

А теперь давайте вернемся к конечным рядам Фурье. Функции Фурье замечательны тем, что они ортогональны не только на непрерывном интервале, но и на множестве отдельных точеке, равноотстоящих друг от друга. Следовательно, вся теория остается той же самой, за исключением того, что в разложении в ряд может быть столько членов, сколько точек в исходном массиве. Для 2N точек, в общем случае, в разложении в ряд присутствует только один член для наивысшей частоты — косинус (так как значение синуса будет равно нулю в точках дискретизации). Коэффициенты определены как суммы значений данных умноженные на соответствующие функции Фурье. Полученное представление, с учётом округления, будет воспроизводить исходные данные.

Вычисление разложения будет выглядеть как 2N операций сложения и умножения для каждого из 2N значений исходных данных, то есть что-то около (2N)² операций сложения и умножения. Использование двух оптимизаций: (1) сложение и вычитание членов с одинаковым множителем перед выполнением операции умножения и (2) вычисление более высоких частот при помощи умножение более низких частот, привело к появлению быстрого преобразования Фурье (БПФ), которое требует N logN операций. Такое уменьшение требуемой вычислительной мощности сильно изменило целые области науки и техники — то, что раньше было невозможно из-за высоких затрат и длительного времени вычисления, стало повсеместно распространено.

А сейчас время еще одной истории из жизни. Все вы слышали про БПФ и публикацию Кули-Тьюки. БПФ иногда называется преобразованием или алгоритмом Кули-Тьюки. Тьюки подсказал мне, отчасти, базовые идеи БПФ. В то время у меня был программируемый внешними перфокартами калькулятор IBM (IBM Card Programmed Calculator), и операция «бабочка», которую он имел в виду, была абсолютно не практичной на оборудовании, которое у меня было. Спустя несколько лет у меня появился программируемый внутри IBM-650, и он мне напомнил об этих оптимизациях еще раз. Все, что я тогда помнил, это то, что это была одна их немногих плохих идей Тьюки; Я абсолютно забыл почему она была плоха — только по из-за ограничений оборудования, которое у меня тогда было. Таким образом я не реализовал БПФ, хотя книга, которую я уже опубликовал к тому моменту, показывает что все необходимое для этого я тогда уже знал, и мог реализовать БПФ очень просто!

Мораль: если вы запомнили, что что-то не может быть сделано, то также запомните основные причины почему это не может быть сделано, чтобы позже, когда обстоятельства изменятся, вы не сказали: «Это не может быть сделано». Подумайте о моей ошибке! Разве может быть что-то глупее? К счастью для моего эго, это распространенная ошибка ( и я ее совершил больше одного раза), но из-за того, что я попал впросак с БФТ, я теперь к очень чутко к ней отношусь. Я также заметил что другие тоже часто ошибаются таким же образом — слишком часто! Пожалуйста, запомните историю о том, каким глупцом я был и какую возможность я из-за этого упустил, и не совершайте такие ошибки сами. Когда вы решаете, что что-то невозможно, не говорите в будущем снова, что это невозможно до того, как вы не изучите во всех деталях, почему вы изначально были правы, когда утверждали, что это невозможно.

Сейчас я должен вернуться к деликатной теме спектра мощности, который равен сумме квадратов двух коэффициентов заданной частоты в области действительных чисел или квадрату модуля в комплексной области. Исследование этого вопроса убедит вас, что эта величина зависит только от самого сигнала и не зависит от расположения точки начала отсчета во времени, в противоположность значениям коэффициентов, которые зависят от расположения точки начала отсчёта. Спектр играет очень важную роль в науке и технике. Это именно спектральные линии открыли черный ящик строения атома и позволили Бору заглянуть вовнутрь. Более новая квантовая механика, появившаяся в 1925 году, все изменила, чтобы бы хоть немного в чем-то уверенным, но спектр по-прежнему оставался ключом. Мы также регулярно исследуем черные ящики посредством изучения зависимостей между спектрами входных и выходных сигналов, чтобы получить понимание об их внутреннем устройстве — заметьте, что оно всегда уникально, но в общем мы получаем достаточно информации, чтобы формировать новые теории.

Позвольте мне аккуратно проанализировать что мы делаем и что мы при этом подразумеваем, потому что это в значительной степени определяет что мы видим в итоге. Обычно, по крайней мере в нашем воображении, мы имеем дело с аналоговым сигналом. Он обычно бесконечный и мы снимаем отсчёты на временном промежутке длиной 2L. Это то же самое, что и умножение сигнала на окно Ланцоша, или прямоугольное окно, если вам так больше нравится. Это означает, что происходит свёртка исходного сигнала с соответствующей функцией вида (sin x)/ x, рисунок 16.V — чем длинее сигнал, тем уже петли (sinx)/x. Каждая чистая спектральная линия растекается по соответствующей (sinx)/x кривой.
Рисунок 16.V
Затем мы производим дискретизацию через равные интервалы времени и высокие частоты накладываются на более низкие частоты. Очевидно, что вне зависимости от порядка этих двух операций — дискретизации и ограничении сигнала по времени — мы получим одинаковый результат. Как я уже упоминал, однажды, я аккуратно проработал соответствующие алгебраические преобразования, чтобы убедиться, что то, что должно быть истинно с точки зрении теории, на самом деле является истинным и на практике.

Затем мы используем ПБФ, которое является всего лишь хитроумным и точным методом получения коэффициентов конечного ряда Фурье. Дело в том, что когда мы допускаем представление сигнала в форме конечно ряда Фурье мы делаем предполагаем, что исходная функция является периодической с длиной периода равной в точности периоду дискретизации умноженному на количество снятых отсчётов. Мы насильно принимаем все негармонические частоты за гармонические — мы насильно превращаем сплошной спектр в линейчатый спектр. Такое отображение не является локальный эффектом, и как вы легко можете посчитать, что негармонические частоты накладываются на все гармонические частоты, конечно, наибольшим образом, на смежные частоты, но при этом, довольно не тривиальным образом, они влияют и на более отдаленные частоты.

Я избегал вычитания среднего значения — стандартного приёма из области статистики, который используется для удобства или калибровки. Такой приём уменьшает амплитуду нулевой частоты в спектре до нуля и привносит серьезный разрыв в спектр. Если в последствии будет использоваться оконная функция, то она просто размажет этот разрыв по смежным частотам. Во время обработки данных для Тьюки, я часто использовал вычитание линейного или даже квадратичного тренда, из данных о полете самолета или ракеты. Но спектр суммы двух сигналов отнюдь не является суммой спектров! При сложении двух функций отдельные частоты складываются алгебраически, и они могут как усилить друг друга так и полностью погасить, и это приведет к абсолютно ложному результату. Линия тренда имеет большой разрыв на конце (помните, что мы предполагаем что функции являются периодическими), потому что ее коэффициенты уменьшаются как 1/k, что совсем не быстро. Мы по-прежнему частично используем их, потому что мы не знаем чем их можно заменить — и никто из тех, кого я знаю, не имеет никаких разумных аргументов против моих замечаний.

Но вернемся к теории. Каждый спектр реального шума уменьшается довольно быстро по мере того, как мы стремимся к бесконечной частоте, иначе он имел бы бесконечную энергии. Но процесс дискретизации сам по себе накладывает более высокие частоты на более низкие, и такое уменьшение полосы, как показано на графике 16.VI, имеет тенденцию приводить к плоскому спектру — помните, что частоты складываются алгебраически. Таким образом существует тенденция наблюдать плоский спектр для шума, и если спектр плоский, то такую шум мы называем белым шумом. Сигнал преимущественно расположен в области низких частот. Это утверждение справедливо по нескольким причинам, включая использование оверсэмплинга (снятие отсчётов более часто, чем того требует теорема Найквиста), который дает нам возможность использовать усреднение для уменьшения погрешности измерения. Таким образом, типичный спектр будет выглядеть как показано на графике 16.VI. Поэтому для удаления шума так распространен фильтр нижних частот. Ни один линейный метод не может отделить сигнал от шума на одной и той же частоте, но шум за пределами частот сигнала может быть удален фильтром нижних частот. Таким образом, когда мы используем оверсэмплинг, у нас есть шансы удалить большую часть шума при помощи фильтра нижних частот.

Помните, что у нас есть неявно ограничение, что мы имеем дело с линейной системой. Анализ фондового рынка при помощи преобразований Фурье показал наличие исключительно белого шума в данных, и это было интерпретировано как невозможность прогнозирования цен на бирже — это правда только если вы используете простые линейные предикторы. Однако, это ничего не говорит о практическом применении нелинейных предикторов. Здесь мы снова можем наблюдать широкое распространение некорректного толкования результатов из-за использования математического инструмента, без понимании фундаментальных основ, которые лежат в его основе. Малое знание — это опасная вещь, особенно если у вас есть пробелы в фундаментальных знаниях.

Я аккуратно упомянул в предисловии к теме о цифровых фильтрах, что в то время, я думал, что я ничего о них не знаю. Чего я тогда не знал — только потому, что я тогда ничего не знал о проектировании рекурсивных цифровых фильтрах- так это того, что я к тому моменту их уже создал, когда я подробно изучал теорию предиктор-корректоров применительно к численному решению обычных дифференциальных уравнений. Корректор — это практически рекурсивный цифровой фильтр!

Когда я изучал как численно проинтегрировать систему обычных дифференциальных уравнений, я был свободен от стереотипов из области цифровых фильтров, и вскоре я сообразил, что ограниченный входной сигнал, как говорят эксперты по цифровым фильтрам, если вы его интегрируете, может вызвать неограниченный сигнал на выходе — что они называли нестабильным, но абсолютно очевидно, что вы должны получить, если вы интегрируете — даже константное значение на входе приведет к линейному росту на выходе. На самом деле, когда я позже столкнулся с задачей посадочной траектории на луну, где нет воздуха, и поэтому нет сопротивления, поэтому нет явной первой производной в уравнении, и я хотел воспользоваться таким решениям используя подходящую формулу для численного интегрирования, я обнаружил, что я у меня был квадратичный рост ошибки; небольшая ошибка округления в вычислении ускорения не будет исправлена и приведет к квадратичной ошибки в определении местоположения; ошибка в ускорении приводит к квадратичному росту ошибки в вычислении местоположения. Это и есть корень проблемы, в отличие от Земли, где сопротивление воздуха играет роль обратной связи и производит коррекцию неправильного ускорения, и как следствие коррекцию ошибки в местоположении.

Таким образом и по сей день я имею отношение к вопросу стабильности цифровых фильтров, под которой понимается не экспоненциальный рост выходного сигнала при ограниченном входном сигнале. При этом полиномиальный рост разрешен, а это уже не является стандартным критерием стабильности, унаследованным от классических аналоговых фильтров, где если он будет не ограничен, то у вас все расплавится — в любом случае, они никогда не рассматривались всерьез как инструмент интегрирования.

Мы рассмотрим это подробнее в следующей главе, которая посвящена рекурсивным фильтрам, которые играют важную роль в интегрировании.

Продолжение следует...

Кто хочет помочь с переводом, версткой и изданием книги — пишите в личку или на почту magisterludi2016@yandex.ru

Кстати, мы еще запустили перевод еще одной крутейшей книги — «The Dream Machine: История компьютерной революции»)