Принцип наименьшего действия. Часть 1 / forpes.ru

Главная
Принцип наименьшего действия. Часть 1

Принцип наименьшего действия. Часть 1 +62

07.10.2018 15:04

andrew526d 155 36200 Источник

Когда я впервые узнал об этом принципе, у меня возникло ощущение какой-то мистики. Такое впечатление, что природа таинственным образом перебирает все возможные пути движения системы и выбирает из них самый лучший.

Сегодня я хочу немного рассказать об одном из самых замечательных физических принципов – принципе наименьшего действия.

Предыстория

Со времен Галилея было известно, что тела, на которые не действуют никакие силы, двигаются по прямым линиям, то есть по кратчайшему пути. По прямым линиям распространяются и световые лучи.

При отражении свет также двигается таким образом, чтобы добраться из одной точки в другую кратчайшим путем. На картинке кратчайшим будет зеленый путь, при котором угол падения равен углу отражения. Любой другой путь, например, красный, окажется длиннее.

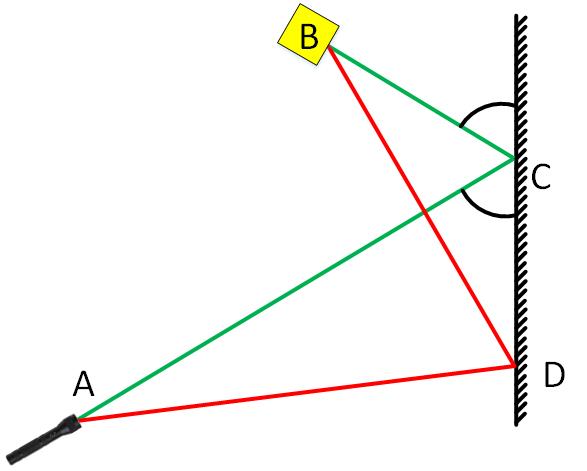
Это несложно доказать, просто отразив пути лучей на противоположную сторону от зеркала. На картинке они показаны пунктиром.

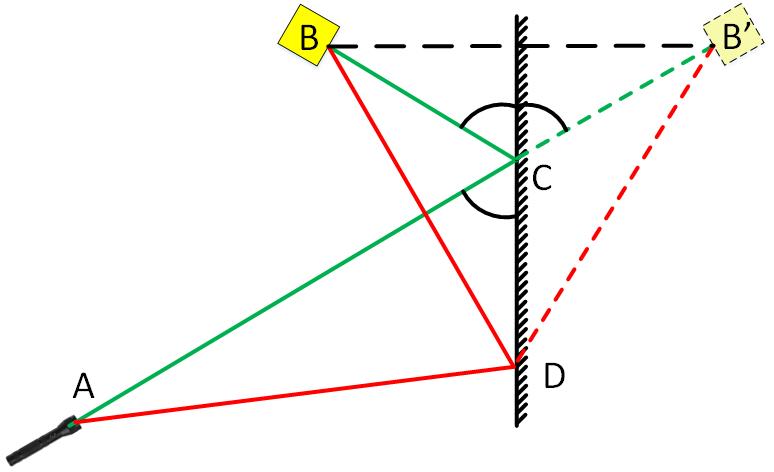
Видно, что зеленый путь ACB превращается в прямую ACB’. А красный путь превращается в изломанную линию ADB’, которая, конечно длиннее зеленой.

В 1662 Пьер Ферма предположил, что скорость света в плотном веществе, например, в стекле, меньше, чем в воздухе. До этого общепринятой была версия Декарта, согласно которой скорость света в веществе должна быть больше, чем в воздухе, чтобы получался правильный закон преломления. Для Ферма предположение, что свет может двигаться в более плотной среде быстрее, чем в разреженной казалось противоестественным. Поэтому он предположил, что все в точности наоборот и доказал удивительную вещь – при таком предположении свет преломляется так, чтобы достичь место назначения за минимальное время.

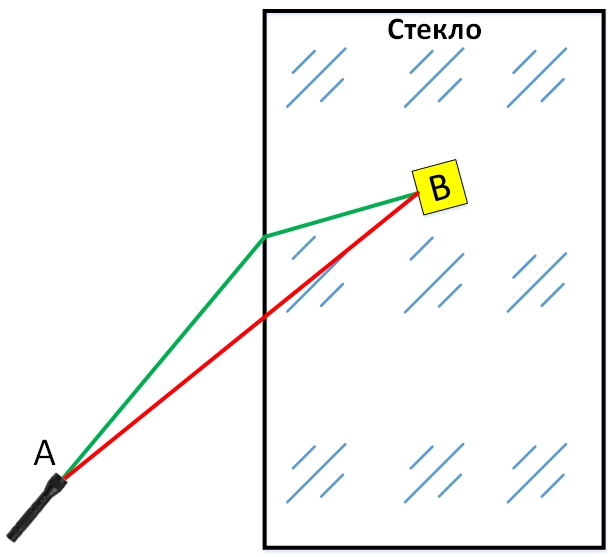
На рисунке опять, зеленым цветом показан путь, по которому в действительности двигается световой луч. Путь, отмеченный красным цветом, является кратчайшим, но не самым быстрым, потому что свету приходится больший путь проходить в стекле, а в нем его скорость меньше. Самым быстрым является именно реальный путь прохождения светового луча.

Все эти факты наводили на мысль, что природа действует каким-то рациональным образом, свет и тела двигаются наиболее оптимально, затрачивая как можно меньше усилий. Но что это за усилия, и как их посчитать оставалось загадкой.

В 1744 Мопертюи вводит понятие «действия» и формулирует принцип, согласно которому истинная траектория частицы отличается от любой другой тем, что действие для неё является минимальным. Однако сам Мопертюи, так и не смог дать четкого определения чему равно это действие. Строгая математическая формулировка принципа наименьшего действия была разработана уже другими математиками – Эйлером, Лагранжем, и окончательно была дана Уильямом Гамильтоном:

На математическом языке принцип наименьшего действия формулируется достаточно кратко, однако не для всех читателей может быть понятен смысл используемых обозначений. Я хочу попытаться объяснить этот принцип более наглядно и простыми словами.

Свободное тело

Итак, представьте, что вы сидите в машине в точке

$inline$ и в момент времени

$inline$ вам дана простая задача: к моменту времени

$inline$ вам нужно доехать на машине до точки

$inline$ .

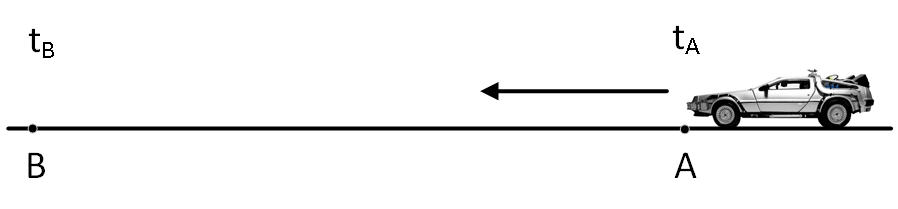
Топливо для машины дорого стоит и, конечно, вам хочется потратить его как можно меньше. Машина у вас сделана по новейшим супер-технологиям и может разгоняться или тормозить как угодно быстро. Однако, устроена она так, что чем быстрее она едет, тем больше потребляет топлива. Причем потребление топлива пропорционально квадрату скорости. Если вы едете в два раза быстрее, то за тот же промежуток времени потребляете в 4 раза больше топлива. Кроме скорости, на потребление топлива, конечно же влияет и масса автомобиля. Чем тяжелее наш автомобиль, тем больше топлива он потребляет. У нашего автомобиля потребление топлива в каждый момент времени равно

$inline$ , т.е. в точности равно кинетической энергии автомобиля.

Так как же нужно ехать, чтобы добраться к пункту

$inline$ к точно назначенному времени и израсходовать топлива как можно меньше? Ясно, что ехать нужно по прямой. При увеличении проезжаемого расстояния топлива израсходуется точно не меньше. А дальше можно избрать разные тактики. Например, можно быстро приехать в пункт

$inline$ заранее и просто посидеть, подождать, когда наступит время

$inline$ . Скорость езды, а значит и потребление топлива в каждый момент времени при этом получится большой, но ведь и время езды сократится. Возможно, общий расход топлива при этом будет не так уж и велик. Или можно ехать равномерно, с одной и той же скоростью, такой, чтобы, не торопясь, точно приехать в момент времени

$inline$ . Или часть пути проехать быстро, а часть медленнее. Как же лучше ехать?

Оказывается, что самый оптимальный, самый экономный способ езды – это ехать с постоянной скоростью, такой, чтобы оказаться в пункте

$inline$ в точно назначенное время

$inline$ . При любом другом варианте топлива израсходуется больше. Можете сами проверить на нескольких примерах. Причина в том, что потребление топлива возрастает пропорционально квадрату скорости. Поэтому при увеличении скорости потребление топлива возрастает быстрее, чем сокращается время езды, и общий расход топлива также возрастает.

Итак, мы выяснили, что если автомобиль в каждый момент времени потребляет топливо пропорционально своей кинетической энергии, то самый экономный способ добраться из точки

$inline$ в точку

$inline$ к точно назначенному времени – это ехать равномерно и прямолинейно, точно так, как двигается тело в отсутствие действующих на него сил. Любой другой способ движения приведет к большему общему расходу топлива.

В поле тяжести

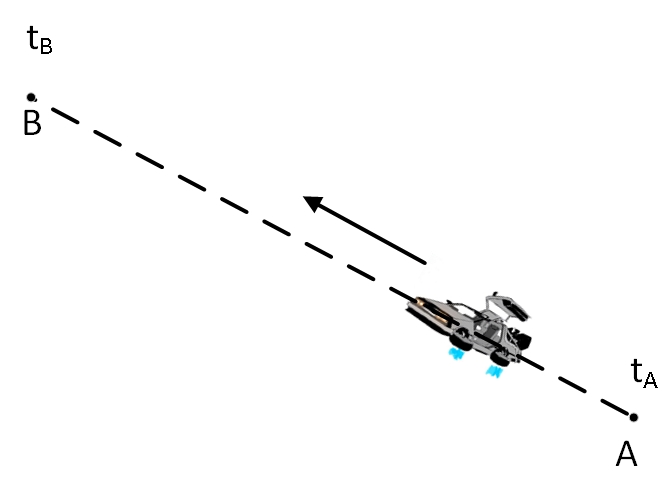
Теперь давайте немного усовершенствуем наш автомобиль. Давайте приделаем к нему реактивные двигатели, чтобы он мог свободно летать в любом направлении. В целом конструкция осталась той же, поэтому расход топлива опять остался строго пропорционален кинетической энергии автомобиля. Если теперь дано задание вылететь из точки

$inline$ в момент времени

$inline$ и прилететь в точку

$inline$ к моменту времени

$inline$ , то наиболее экономичный способ, как и прежде, конечно, будет лететь равномерно и прямолинейно, чтобы оказаться в точке

$inline$ в точно назначенное время

$inline$ . Это опять соответствует свободному движению тела в трехмерном пространстве.

Однако, в последнюю модель автомобиля установили необычный аппарат. Данный аппарат умеет вырабатывать топливо буквально из ничего. Но конструкция такова, что чем выше находится автомобиль, тем больше топлива в каждый момент времени вырабатывает аппарат. Выработка топлива прямо пропорциональна высоте

$inline$ , на которой в данный момент находится автомобиль. Также, чем тяжелее автомобиль, тем более мощный аппарат на нем установлен и тем больше топлива он вырабатывает, и выработка прямо пропорциональна массе автомобиля

$inline$ . Аппарат получился таким, что выработка топлива точно равна

$inline$ (где

$inline$ – ускорение свободного падения), т.е. потенциальной энергии автомобиля.

Потребление топлива в каждый момент времени получается равным кинетической энергии минус потенциальной энергии автомобиля (минус потенциальной энергии, потому что установленный аппарат вырабатывает топливо, а не тратит). Теперь наша задача наиболее экономного движения автомобиля между пунктами

$inline$ и

$inline$ становится сложнее. Прямолинейное равномерное движение оказывается в данном случае не самым эффективным. Оказывается, более оптимально — немного набрать высоты, какое-то время там задержаться, выработав побольше топлива, а затем уже спуститься в точку

$inline$ . При правильной траектории полета общая выработка топлива за счет набора высоты перекроет дополнительные расходы топлива на увеличение длины пути и увеличения скорости. Если аккуратно посчитать, то самым экономным способом для автомобиля будет лететь по параболе, точно по такой траектории и с точно такой скоростью, с какой летел бы камень в поле тяжести Земли.

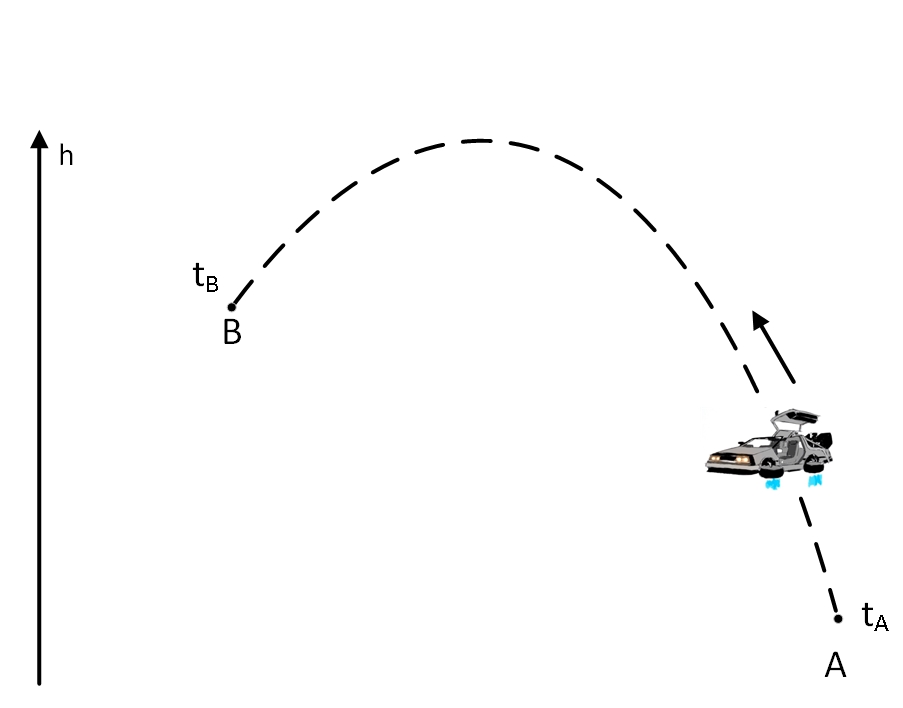
Здесь стоит сделать разъяснение. Конечно, можно из точки

$inline$ кинуть камень многими разными способами так, чтобы он попал в точку

$inline$ . Но кидать его нужно так, чтобы он, вылетев из точки

$inline$ в момент времени

$inline$ , попал в точку

$inline$ точно в момент времени

$inline$ . Именно это движение будет самым экономным для нашего автомобиля.

Функция Лагранжа и принцип наименьшего действия

Теперь мы можем перенести эту аналогию на реальные физические тела. Аналог интенсивности потребления топлива для тел называют функцией Лагранжа или Лагранжианом (в честь Лагранжа) и обозначают буквой

$inline$ . Лагранжиан показывает насколько много «топлива» потребляет тело в данный момент времени. Для тела, движущегося в потенциальном поле, Лагранжиан равен его кинетической энергии минус потенциальной энергии.

Аналог общего количества израсходованного топлива за все время движения, т.е. значение Лагранжиана, накопленное за все время движения, называется «действием».

Принцип наименьшего действия состоит в том, что тело двигается таким образом, чтобы действие (которое зависит от траектории движения) было минимальным. При этом не нужно забывать, что заданы начальное и конечное условия, т.е. где тело находится в момент времени

$inline$ и в момент времени

$inline$ .

При этом тело не обязательно должно двигаться в однородном поле тяготения, которое мы рассматривали для нашего автомобиля. Можно рассматривать совершенно другие ситуации. Тело может колебаться на резинке, качаться на маятнике или летать вокруг Солнца, во всех этих случаях оно движется так, чтобы минимизировать «общий расход топлива» т.е. действие.

Если система состоит из нескольких тел, то Лагранжиан такой системы будет равен суммарной кинетической энергии всех тел минус суммарной потенциальной энергии всех тел. И опять, все тела будут согласованно двигаться так, чтобы действие всей системы при таком движении было минимальным.

Не все так просто

На самом деле я немного обманул, сказав, что тела всегда двигаются так, чтобы минимизировать действие. Хотя в очень многих случаях это действительно так, можно придумать ситуации, в которых действие явно не минимально.

Например, возьмем шарик и поместим его в пустое пространство. На некотором отдалении от него поставим упругую стенку. Допустим, мы хотим, чтобы через некоторое время шарик оказался в том же самом месте. При таких заданных условиях шарик может двигаться двумя разными способами. Во-первых, он может просто оставаться на месте. Во-вторых, можно его толкнуть по направлению к стенке. Шарик долетит до стенки, отскочит от нее и вернется обратно. Понятно, что можно толкнуть его с такой скоростью, чтобы он вернулся в точно нужное время.

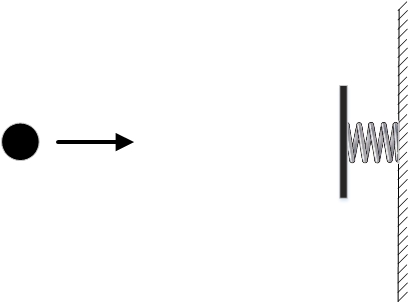
Оба варианта движения шарика возможны, но действие во втором случае получится больше, потому что все это время шарик будет двигаться с ненулевой кинетической энергией.

Как же спасти принцип наименьшего действия, чтобы он был справедлив и в таких ситуациях? Об этом мы поговорим в следующий раз.

Комментарии (155)

maisvendoo
07.10.2018 20:00
#19203259
но действие во втором случае получится больше, потому что все это время шарик будет двигаться с ненулевой кинетической энергией

Как это? В момент максимального сжатия пружина скорость шарика будет равна нулю, соответственно и кинетическая энергия тоже.

Если же Вы имеете в виду абсолютно упругий удар, то как это Вы так лихо применяете интегральный принцип к разрывной функции? Функция Лагранжа в этому случае терпит разрыв в момент упругого удара, так как вектор скорости резко меняет свое направление
1. vassabi
  07.10.2018 20:16
  #19203279
  а почему резко? Там же вроде как работает упругость шарика (по закону Гука), и вектор скорости спокойно и без разрывов переходит через 0.
  1. SandroSmith
    07.10.2018 20:32
    #19203319
    Это первая половина сообщения maisvendoo. В случае абсолютно упругого удара таки да, будет разрыв.
1. andrew526d Автор
  07.10.2018 21:14
  #19203407
  Если быть точным, то maisvendoo, конечно, прав. В момент максимального сжатия пружины кинетическая энергия шарика будет равна нулю. Поэтому правильно сказать, что «все это время шарик будет двигаться с ненулевой кинетической энергией, за исключением одного мгновения, в момент максимального сжатия пружины». Но я в данном случае не стремился к абсолютной строгости. Если шарик достаточно далеко расположен от пружины, то основная часть действия накапливается во время его свободного полета от начального положения до пружины и обратно. Поэтому, при достаточном удалении шарика от пружины, действие при таком движении будет заведомо больше, чем при состоянии покоя. Собственно, это я и хотел сказать.
  1. maisvendoo
    08.10.2018 07:40
    #19204165
    Стоп-стоп-стоп. Приводя последнюю задачу в качестве примера, Вы поступаете некорректно во всех случаях. Если считать стенку линейно упругой, поместить начало координат на стенку, а ось х выпустить влево по нормали к ней, то тогда можно записать потенциальную энергию шарика
    
    $\Pi(x) = \begin{cases}\cfrac{c\,x^2}{2}, \quad x <=0\\0,\quad x> 0\end{cases}$
    
    Тогда функция Лагранжа
    
    $L(x, \dot x) = T(\dot x) - \Pi(x) = \cfrac{m\,\dot x^2}{2} - \Pi(x)$
    
    имеет разрыв первого рода. Эта система не относится к консервативным, о каком применении принципа наименьшего действия для анализа её движения может идти речь, когда получение уравнений движения путем минимизации функционала действия справедливо лишь для консервативных систем?
    
    andrew526d Автор
    08.10.2018 08:09
    #19204219
    Не очень понял, а где разрыв? Вроде функция получилась везде непрерывной, и даже непрерывно дифференцируемой.
    
    maisvendoo
    08.10.2018 09:05
    #19204339
    Эта функция кусочно-непрерывна, но уже первая её производная по x имеет особую точку x = 0, а вторая производная — имеет разрыв второго рода в этой точке.
    
    Ну да бог с ним, хорошо. Ваша ошибка гораздо более фундаментальна, чем я писал ранее. Вы пытаетесь ловить блох там где их нет, решая давно решенную задачу. Вот смотрите, задача отыскания траектории движения сводится к вариационной задаче отыскания экстремали для функционала действия
    
    $S = \int\limits_{t_1}^{t_2}L(x(t), \dot x(t)) dt \to \min$
    
    Так эта задача уже давно имеет общее решение, которое выглядит так
    
    $\frac{d}{dt}\left(\frac{\partial L}{\partial \dot x}\right) - \frac{\partial L}{\partial x} = 0$
    
    с последующим отысканием x(t) путем решения данного дифференциального уравнения при заданных начальных условиях
    
    при этом, постановке любой вариационной задачи сопутствует задание краевых условий на искомую функцию, в рамках которой она и решается. Вы этот факт напрочь игнорируете, рассуждая о том, что при действие при изначально покоящемся шарике меньше, чем действие в случае его движения в сторону стены с последующим отскоком.
    
    Говоря так, вы рассматриваете две различных вариационных задачи! В обоих случаях действие по Гамильтону будет минимально, с учетом начальных условий на фазовую траекторию шарика
    
    $x(t_1) = x_0,\quad \dot x(t_1) = v_0$
    
    Так что противоречие, которое Вы намерены решать во второй части, при всём уважении, Вам приснилось. Пытаясь объяснять на пальцах вариационные принципы механики вы до конца не понимаете лежащий в основе математический аппарат
    
    andrew526d Автор
    08.10.2018 09:24
    #19204393
    Дело в том, что в ПНД в краевых условиях не фигурируют скорости. Нужно только, чтобы правильными были начальное и конечное положение шарика. А они в обоих случаях совпадают.
    Дело не в этом. Сам принцип ПНД нужно немного уточнить, что я и сделаю во 2-й части. Так что никакого противоречия не будет.
    
    maisvendoo
    08.10.2018 09:37
    #19204433
    Нужно только, чтобы правильными были начальное и конечное положение шарика
    
    Откуда мы знаем конечное положение шарика, если мы не знаем интегралов движения? И в случае отскока в пустой, как вы пишете, среде шарик не остановится в своем начальном положении а проследует его с постоянной скоростью, равной скорости отскока.
    
    В данном случае, правильнее говорить, что у нас наложено одно краевое условие на начальную точку фазовой траектории, определяемой в пространстве двух параметров — координаты и её производной по времени.
    
    Ещё раз говорю, что нет никакого тут противоречия, Вы его придумывате — действие достигает минимума в случае с отскоком, на всем множестве виртуальных траекторий при заданных начальных условиях
    
    maisvendoo
    08.10.2018 10:24
    #19204645
    И вообще, где написано, что точки фазовой траектории фиксированы? Речь идет об изохронных вариациях и соответственно лишь о фиксированных моментах времени t1 и t2
    
    Читаем, например вот эту книгу со страницы 91 и далее
    
    totally_nameless
    08.10.2018 22:24
    #19207439
    У вас лагранжиан зависит от двух независимых переменных — обобщенных координаты и скорости, соответсвенно, если скорости разные в начальный момент времени, то это разные действительно вариацонные задачи.
    
    maisvendoo
    08.10.2018 22:34
    #19207459
    И я о том же толкую. Вариации обобщенных координат и обобщенных скоростей есть независимые вариации. И теперь заинтригован, о чем же будет вторая статья.
    
    Одно дело популярно излагать для понимания зубодробительную математику, а другое — паразитировать на этом процессе, придумывая сущности и превозмогая трудности, которых в реальности нет. В целом статья была бы хороша, если бы ни этот пунктик автора с загадкой, которую он планирует разгадать в следующей статье. Хотя на самом деле, загадки никакой и нет
    
    totally_nameless
    08.10.2018 22:40
    #19207469
    +1
    Автор все равно молодец. И обсуждение поднял и сам в итоге разберется.
    
    maisvendoo
    08.10.2018 22:46
    #19207495
    +1
    Автор все равно молодец
    
    С эти не спорю
    
    andrew526d Автор
    08.10.2018 23:10
    #19207545
    Возможно, я не очень хорошо объяснил, давайте попробую еще раз.
    
    Давайте разберем сначала простейший случай — шарик, свободно двигающийся в пространстве. Для него заданы следующие условия:
    1. в момент времени tA он вылетел из точки A.
    2. в момент времени tB он прилетел в точку B.
    
    Все, больше никаких условий, никаких начальных или конечных скоростей, ничего задавать не нужно. Из ПНД в данном случае однозначно определяется траектория движения шарика. Его траектория оказывается такова, что действие при такой траектории минимально по сравнению с действием при любой другой траектории. Можно взять любые траектории движения, с какими угодно скоростями, лишь бы выполнялись условия 1 и 2. При всех траекториях действие будет больше, чем при истинной траектории движения шарика.
    
    Скорость не ЗАДАЕТСЯ, она в любой момент времени ОПРЕДЕЛЯЕТСЯ принципом наименьшего действия (поскольку наименьшим действием обладает прямолинейная траектория с постоянной скоростью, то скорость для этой траектории оказывается равна расстоянию от A до B деленной на tB-tA).
    
    andrew526d Автор
    08.10.2018 23:37
    #19207619
    Для движения шарика в поле тяжести все то же самое. Просто Лагранжиан зависит не только от кинетической энергии (скорости шарика), но и от потенциальной (положения шарика). Если для шарика заданы условия:
    
    1. в момент времени tA он вылетел из точки A.
    2. в момент времени tB он прилетел в точку B.
    
    То опять его траектория, в том числе начальная скорость однозначно ОПРЕДЕЛЯЕТСЯ ПНД. Кроме условий 1 и 2 никаких других условий не нужно. И именно зафиксировав только эти условия и нужно сравнивать различные траектории.
    
    maisvendoo
    08.10.2018 23:57
    #19207649
    2. в момент времени tB он прилетел в точку B.
    
    Кто Вам сказал, что в момент времени tB шарик будет именно в точке B? В соответсвии с ПНД фиксирован только момент времени tB, а фазовые координаты могут быть любыми! Не путайте пожалуйста ПНД с задачей о стрельбе.
    
    Почитайте в конце концов книги по аналитической механике
    
    Скорость не ЗАДАЕТСЯ, она в любой момент времени ОПРЕДЕЛЯЕТСЯ принципом наименьшего действия
    
    Вы понимаете что мелете вообще? Если вы не зададите начальных условий вообще, то решая задачу минимизации функционала действия вы получаете не одну траекторию, а бесконечное их множество, задаваемое областью значений констант интегрирования, которых 2*s, где s — число степеней свободы системы.
    
    И все, абсолютно все траектории из полученного множества будут доставлять функционалу действия минимум! Только фактическое значение этого минимума будет различаться, в зависимости от конкретных начальных условий.
    
    Черт возьми, прекратите изображать из себя Петрушку и учите матчасть!
    
    andrew526d Автор
    09.10.2018 00:28
    #19207715
    Кто Вам сказал, что в момент времени tB шарик будет именно в точке B?
    
    Именно так формулируются граничные условия для ПНД.
    
    Могу только сослаться на упоминавшегося Ландау-Лившица.
    
    Как видите, задаются только координаты в моменты времени t1 и t2. Никаких заданных начальных скоростей в ПНД нет.
    
    maisvendoo
    09.10.2018 00:34
    #19207737
    Да, когда мы вычисляем действие, по известной траектории движения, мы знаем положения точки в указанные моменты времени.
    
    Когда мы решаем вариационную задачу по минимизации действия, мы работаем с бесконечно малыми изохронными вариациями фазовых координат.
    
    Я вам о том и толкую, что рассматривая покоящийся шарик вы рассматриваете одну траекторию доставляющую минимум функционалу действия, а рассматривая шарик, отскакивающий от стенки — вы рассматриваете другую траекторию, доставляющую минимум функционалу действия.
    
    Вы сравниваете два минимума функционала действия в разных задачах, Вы понимаете это или нет?
    
    Пока я вижу, что вы в корне неверно понимаете ПНД. Покоящийся шарик именно потому и покоится, что данное его кинематическое состояние доставляет минимум действию по Гамильтону, среди множества других гипотетически возможных в данной ситуации кинематических состояний. Вникните в эту фразу, пожалуйста.
    
    andrew526d Автор
    09.10.2018 00:39
    #19207749
    Давайте двигаться постепенно. Вы для свободного шара со мной согласны?
    
    Что если него заданы следующие условия:
    1. в момент времени tA он вылетел из точки A.
    2. в момент времени tB он прилетел в точку B.
    
    То из ПНД в данном случае однозначно определяется траектория движения шарика.
    
    maisvendoo
    09.10.2018 00:52
    #19207775
    Почему Вы упорно пытаетесь сравнивать действие на двух действительных траекториях шарика? Действительная траектория как раз и доставляет минимум функционалу действия. Больше этой величины может быть только действие на любой другой физически невозможной траектории при данных начальных условиях.
    
    Tyusha
    09.10.2018 15:34
    #19210243
    Кто Вам сказал, что в момент времени tB шарик будет именно в точке B? В соответсвии с ПНД фиксирован только момент времени tB, а фазовые координаты могут быть любыми! Не путайте пожалуйста ПНД с задачей о стрельбе.
    
    Если вы не зададите начальных условий
    
    Вообще-то в ПНД ставится не задача Коши, а краевая задача. Так что автор прав, а вы нет.
    
    maisvendoo
    09.10.2018 18:15
    #19210933
    Автор пишет охинею! Откройте учебник по аналитической механике и прочтите внимательно параграф о ПНД. В этой краевой задаче «края» подвижны, и в этих краях условия налагаются не на обобщенные координаты а на их вариации в заданные моменты времени. И результат решения этой вариационной задачи не одна кривая траектории, а множество траекторий, каждая из которых доставляет минимум исследуемому функционалу.
    
    Краевая задача для ОДУ, и задача поиска эктремали для заданного функционала — это две разные задачи. Решение первой дает на выходе одну единственную траекторию, определяемую краевыми условиями. Вторая на выходе дает дифференциальное уравнение, решая которое мы находим интегралы движения, то есть семейство траекторий. Вы понимаете разницу?
    
    Короче говоря, учебник теормеха и вариационного исчисления проштудировать не помешает, ни Вам, ни автору
    
    Druu
    09.10.2018 20:33
    #19211447
    Автор пишет охинею! Откройте учебник по аналитической механике и прочтите внимательно параграф о ПНД. В этой краевой задаче «края» подвижны, и в этих краях условия налагаются не на обобщенные координаты а на их вариации в заданные моменты времени.
    Открыл "лекции по аналитической механике" Гантмахера, края фиксированы.
    
    maisvendoo
    09.10.2018 20:45
    #19211497
    края фиксированы
    
    В краях задана функция q(t), то есть существует действительный закон движения. Значения q(t1) и q(t2) могут быть любыми, удовлетворяющими многообразию траекторий, вытекающему из уравнений движения. А вот вариации q(t) в краях как раз таки фиксированы, что допускает наличие существование окольных движений везде, кроме краев при t1 и t2. Еще раз для тех кто в танке — это не краевая задача для ОДУ, это вариационная задача!
    
    Кто-то из комментаторов выше понимает разницу между приращением обобщенной координаты и её вариацией? Между функцией и функционалом?
    
    totally_nameless
    09.10.2018 00:25
    #19207707
    А можете вывести скорость как функцию времени исходя только из ПНД и начальных координат? Это бы остановило все вопросы…
    
    maisvendoo
    09.10.2018 00:27
    #19207711
    Согласен, коллега. Аналитику в студию!
    
    andrew526d Автор
    09.10.2018 00:36
    #19207743
    Для нахождения траектории с минимальным действием используются уравнения Эйлера-Лагранжа. Например, в случае свободного шара они приводят к уравнению V=константа.
    
    Константа находится из граничных условий:
    1. в момент времени tA он вылетел из точки A.
    2. в момент времени tB он прилетел в точку B.
    
    т.е. V = (B-A)/(tB-tA).
    
    totally_nameless
    09.10.2018 00:53
    #19207781
    Во-первых, уравнения Эйлера-Лагранжа выводятся из ПНД, а не используются для его формулировки, не путайте пожалуйста причину и следствие.
    Во-вторых, не пропускайте выкладки. Давайте начнем с записи лагранжиана и потом уравнений движения для свободного шара и только потом будем выписывать решение.
    Подсказка — там будет вторая производная по времени — ускорение.
    
    maisvendoo
    09.10.2018 00:57
    #19207785
    Автор напрашивается на то, чтобы его публично натыкали носом в лужу, как паршивого котенка. Я могу это устроить, учитывая его твердолобость в отстаивании своей блажи открыть загадку в очевидном.
    
    totally_nameless
    09.10.2018 01:07
    #19207805
    del
    
    maisvendoo
    09.10.2018 01:13
    #19207819
    Сообществу интересно, но в заключении статьи имеется глупая посылка с намеком на продолжение. Я, на всякий случай сделал скрин этого места и буду писать опровержение. Взялся объяснять на пальцах сложные вещи — будь добр разобраться в них на сложном уровне, а не измышлять. Автору похоже не доходит, что он сравнивает действие на двух действительных траекториях и пытается наскрести на этом какой-то материал. Я за чистоту материалов, по крайней мере в хабе «Математика»
    
    totally_nameless
    09.10.2018 01:11
    #19207813
    Зачем? Давайте лучше вместе разберемся, смотрите сколько комментариев к статье, сообществу явно интересно. Хотя я вас понимаю :)
    Есть кстати более тонкий вопрос, не затронутый автором: почему лагранжиан зависит только от нулевой и первой производной обобщенных координат и не зависит от производных высших порядков?
    
    P.S. какой-то треш с уровнями комментариев…
    
    maisvendoo
    09.10.2018 01:14
    #19207829
    Есть кстати более тонкий вопрос, не затронутый автором: почему лагранжиан зависит только от нулевой и первой производной обобщенных координат и не зависит от производных высших порядков?
    
    Потому что в природе нет активных сил, зависящих от ускорения и его производных.
    
    Даже то что я сказал выше избыточно — лагранжиан определяется кинетической и потенциальной энергией системы. Кинетическая энергия по определению зависит от обобщенных координат и скоростей, а потенциальная потому и потенциальная, что определяется только положением системы, определяемым вектором обобщенных координат
    
    totally_nameless
    09.10.2018 02:08
    #19207905
    Я знаю, что вы знаете
    
    gks
    09.10.2018 16:13
    #19210425
    Дедушка Эйнштейн, с вами не согласился бы. У него нет потенциальной энергии.
    Как возникает там кинетическая энергия. Исследуем функцию Лагранжа в инерциальных системах. То есть она однородна и изотропна. То есть функция Лагранжа для инерциальной системы может быть выражена как L(v^2). Для малых скоростей L(v^2) ~ v^2/2 = mv^2/2
    Тогда мы можем попытаться найти вид функции Лагранжа L(q, q', t) = L(q'^2) — U(q). Функцию времени можем исключить, так как функция Лагранжа определена с точностью до функции времени.
    Ищем с минусом, чтоб получить некий физический уже известный смысл этой функции. Чтоб получилось уравнение Ньютона. Можно искать с плюсом, тогда нужно будет придумывать некую обратную потенциальную энергию. То есть ваше утверждение
    
    лагранжиан определяется кинетической и потенциальной энергией системы
    
    Не верно в общем виде. Принцип наименьшего действия работает и при скоростях близких к скорости света.
    L = m*c^2/sqrt(1-v^2/c^2) А потенциальной и кинетической энергии нету.
    
    maisvendoo
    09.10.2018 18:26
    #19210973
    Мы говорим о классической механике. Об общих видах тут речи не идет, тут бы с частным примером разобраться кое-кому
    
    andrew526d Автор
    09.10.2018 01:35
    #19207865
    К сожалению, у нас с вами не получается конструктивно го диалога. Хорошо, давайте останемся каждый при своём мнении.
    
    maisvendoo
    09.10.2018 01:42
    #19207873
    не получается конструктивно го диалога
    
    … по причине того, что в область, где работает чистая математика, примешиваются умозрительные рассуждения основанные на в корне неверных исходных посылках. В таких ситуациях помогает холодный душ, который я Вам с удовольствием пропишу
    
    totally_nameless
    09.10.2018 02:10
    #19207909
    По настоящему конструктивным такой диалог может быть только с формулами.

dilukhin
07.10.2018 20:29
#19203309
Спасибо! Наконец-то понял, что такое этот лагранжиан. Принцип наименьшего действия, вот в чём он зарыт!

SmithV
07.10.2018 20:50
#19203353
+3
Прекрасная статья, из которой следует всем известный закон: лень — движитель прогресса!

Alexey2005
07.10.2018 21:42
#19203455
А нельзя ли использовать эту способность природы извлекать из ниоткуда сразу оптимальное решение? Например, чем решать задачу коммивояжёра алгоритмическими методами, просто изготовить физическую модель задачи, после чего сразу, мгновенно, получить решение прямым измерением?
1. dilukhin
  07.10.2018 22:09
  #19203517
  Можно. Квантовый компьютер её использует — из всего богатства выбора отсекает все неоптимальные варианты. Ричард Фейнман первый пришёл к этой мысли (и потому считается прародителем квантовых вычислений).
  www.mathnet.ru/into214 и ru.wikipedia.org/wiki/Алгоритм_Гровера, например. Берегите мозг.
1. caballero
  08.10.2018 02:50
  #19203911
  И будете городить физическую модель под каждую задачу? Компьютеры тогда зачем изобрели? Находите лагражиан, втыкаете его в уравнение Эйлера-Лагранжа, решаете и получаете траекторию.
  1. San_tit
    08.10.2018 07:16
    #19204101
    К сожалению, не все так просто, как вы описали… Есть сложные системы, где такой подход почти невозможен и используются более экзотические… Правда вот делать под них физические модели тоже может оказаться трудным делом.
    
    caballero
    08.10.2018 11:53
    #19205051
    разумеется. В этом и смысл — иногда проще считать через обычный второй закон Ньютона, иногда через лагранжиан иногда через гамильтониан. В квантовой механике например рулит гамильтонова интерпретация. Физическое моделирование имеет смысл если вы делаете некий прототип и на нем проверяете. Типа как модели в аэродинамической трубе.
1. klirichek
  08.10.2018 08:05
  #19204207
  В Советском Союзе на таком "физическом компьютере" решали дифуры 4-го порядка. Гидравлический интегратор Лукьянова.
1. Wizard_of_light
  08.10.2018 15:05
  #19205931
  Можно, на аналоговых компьютерах вначале так делали. Но цифровые их обошли по универсальности, точности и устойчивости к ошибкам. Да и по скорости во многом догнали. Но физическое моделирование и сейчас применяется, хоть зачастую уже как дополнение к цифровым расчётам — аэродинамическая труба в авиастроении, как пример.

andyudol
07.10.2018 21:53
#19203485
ПНД действует не только в случае движения тел. Например, если разрывать ткань, то разрыв пойдёт вдоль основы или утка (если она новая и качественная — если, например, гнилая, то пожет пойти как угодно).
1. khim
  07.10.2018 23:00
  #19203613
  сли, например, гнилая, то пожет пойти как угодно
  Не как «угодно», а в соответствии с ПНД. Просто если ткань гнилая, то она, скорее всего, неоднородная — и получается как в случае с преломлением: идти по кратчайшей траектории — невыгодно.
  1. SwingoPingo
    08.10.2018 08:20
    #19204247
    Есть еще одно определение «траектория движения воды», которая показывает что многие системы в природе не способны «работать в кредит» ради уменьшения общих итоговых затрат. К примеру та же вода. Или луч, не способный обойти препятствие. Все далеко не так магически, как хотелось бы.
    
    Wizard_of_light
    08.10.2018 15:09
    #19205947
    Вода иногда умеет, только ей внешнее давление нужно и хороший ~~кредитный план~~ сифон.

catharsis
07.10.2018 23:49
#19203703
С функциии Лагранжа и принципа наименьшего действия начинается первый том "Механика" учебника теоретической физики Ландау и Лифшица.
Понять это в формальных определениях без опыта нереально, принять как есть или перескочить первую же главу довольно сложно.
Я думаю это одна из причин, по которым теорфиз и даже теормех считается жестиловом, а ландафшиц слишком сложным. Нужен какой-то переходный учебник для учеников/студентов, освоивших общефиз, но ещё не знакомых с теорфизом.
1. caballero
  08.10.2018 02:44
  #19203905
  ЛЛ даже не для студентов это для продвинутых которые хотят пролвинутся дальше. Лагранжева и гамильтонова механика неплохо описаны в первом томе Сасскинда Теоретическмй минимум.
  1. SwingoPingo
    08.10.2018 08:24
    #19204253
    Но нельзя не заметить что многие вещи у Л&Л очень виртуозно описаны, читаешь как хороший роман. Именно из за этого ощущения «математического волшебства» очень рекомендую Л&Л даже для начинающих.
    
    caballero
    08.10.2018 11:54
    #19205057
    Вот только начинающие вряд ли владеют матапаратом на таком уровне
    
    SwingoPingo
    08.10.2018 14:25
    #19205729
    Согласен
1. Tyusha
  08.10.2018 12:09
  #19205107
  Считать ЛЛ учебником можно только с большой натяжкой. Читать его желательно, только уже имея базовое понимание того, о чём собираешься читать. Вот такой парадокс.
  
  Это библия, которая доходит не с первого, не со второго и даже не с третьего раза. ЛЛ можно открывать, уже повзрослел, и находить там новые нюансы, мимо которых проходила мимо в студенческие.

RuK
07.10.2018 23:56
#19203717
+1
Мне кажется, что совершенно не правильно стараться объяснять физические явления через макро-аналогии (например движение света через движение автомобиля). На то есть 2 причины —
1. Это всё равно не даёт человеку понять суть события.
2. Это приводит к искажению смысла. (как было с «Эффектом наблюдателя», который многие понимают как некий «мистический» как раз из-за неудачного названия и неуместных аналогий)
P.S. Не могу не вспомнить и про «Теорию относительности», которую большенство (!) населения планеты считают постулирующей ни что иное, как — «Всё в мире относительно». )))
1. Tyusha
  08.10.2018 12:17
  #19205151
  Согласна. Нам то сразу понятно откуда «растут колёса» у машины с расходом топлива как квадрат скорости. Но вряд ли такая аналогия упрощает понимание тому, кто впервые слышит о ПНД.
  
  ПНД удивителен, поэтому я разделяю стремление автора поделиться этим чудом с другими. У самой руки чешутся. Но в итоге понимаю, что лучше чем Фейнман в «Лекциях» не напишешь.

caballero
08.10.2018 02:57
#19203917
А вот интересно если взять две соеклянные пластинки с разным кожффициетом преломления и сложить их. Свет пойдет преломлятся по очереди или будет какаято общая оптимальная траектрия в которой углы преломления будут не такие как в пластинках по отдельности?
1. andrew526d Автор
  08.10.2018 07:13
  #19204089
  Свет пойдет преломляться по очереди, что и будет общей оптимальной траекторией.
  1. caballero
    08.10.2018 11:48
    #19205027
    почему то казалось что при наличии второй пластинки угол преломления на первой изменится для получения какой то общей более оптимальной траектории

lxsmkv
08.10.2018 04:49
#19203993
Природа, конечно же не знает ни о каких принципах. Это мы пытаемся сформулировать достаточно простой и доходчивый для нашего ограниченного понимания принцип, чтобы описать то, что мы наблюдаем вокруг себя, в нашей системе условностей.
1. vladdou
  09.10.2018 07:10
  #19208101
  Именно так!

wtigga
08.10.2018 05:21
#19204009
+1
А откуда луч света знает конечную точку назначения, чтобы «оптимально» ней стремиться? По-моему тут перепутаны причина и следствие: свет достигает какой-то точки, потому что пошёл именно этим путём, а не выбирает путь, чтобы достичь именно этой точки.
1. customizer
  08.10.2018 07:57
  #19204199
  Он не знает, у него нечем знать и ничего не выбирает, так как выбирать не из чего. Он движется по единственно возможному пути. Все остальные для него более затратные.
  Собственно, перемещение эл.маг. волн можно упрощенно рассматривать как следствие перемещения заряда (т.е. электрического тока), который движется по пути с наименьшим сопротивлением из-за того, что на всех остальных направлениях нет разности потенциала с движущимся зарядом (они равны по величине и по знаку, и поэтому отталкиваются друг от друга).
  1. klirichek
    08.10.2018 08:11
    #19204229
    По своему единственно возможному пути он и достигает некоей единственно возможной точки, а вовсе не заданной "точки Б".
    А дальше остаётся либо поставить эту самую точку в то место, куда достиг свет.
    Либо начать шерудить источником так, чтобы он попал в нужную нам точку.
    Либо если ничего из этого невозможно, сперва рассчитать траекторию с помощью формул, и настроить источник, чтобы пустить луч именно в рассчитанное направление.
1. brzsmg
  08.10.2018 08:28
  #19204261
  Что бы что то пройти, нужно время. А у фотона его нет.
  Значит для него это мгновенное перемещение.
  Значит конечная и начальная точки равны.
  Путь фотона — это что то виртуальное, «перенос» энергии с задержкой зависимой от минимального расстояния между точками.
  1. caballero
    08.10.2018 12:04
    #19205085
    +1
    так и есть. Электрон испуская фотон передает энергию. виртуальному квантовому осциллятору в вакууме а тот передает его другому электрону через какое то время. То есть фотон не то что никуда не летит — по сути то виртуальное понятие — мы не можем наблюдать движущийся фотон.
1. caballero
  08.10.2018 12:12
  #19205119
  вот и вопрос — почему именно этим и каждый раз именно этим
  1. swelf
    08.10.2018 16:55
    #19206433
    А чего ему вообще как-то по разному в стабильной среде двигаться то?) Мне кажется тут что-то не верно в статье объяснено. При прямолинейном движении в своей среде, луч в точку А не может попасть по другому пути в принципе. Картинка вообще вносит путаницу, нарисован красный луч с тем подтекстом, что если убрать стекло, то луч сам по себе пойдет по красной линии так как она в данном случае короче, но это же не так, он пойдет по зеленой, но не преломится и пойдет дальше. И каким образом эта картинка показывает оптимальную траекторию… Луч пришел в точку А, мы нарисовали до нее прямую красную, назвали ее оптимальной, хотя свет по ней не направлен и в принципе не пойдет хоть есть стекло хоть нету.
    
    swelf
    08.10.2018 17:37
    #19206611
    Хотя если посмотреть на это с чуть более другой стороны. Из мира квантовой физики. То у фотона есть точка начала пути и точка конца пути и потом он уже ищет траекторию среди миллионов самых разных траекторию. С этой точки зрения, красная линия и правда валидная траектория и самая короткая с геометрической точки зрения.
    Это как в анекдоте из ТБВ
    Изо дня в день физик приходит в кафе и заказывает 2 порции мороженного, одну для себя, вторую ставит напротив. Спустя несколько дней официант не выдерживает и спрашивает
    -Что вы делаете?
    -Понимаете, я физик, и с точки зрения квантовой механики, есть вероятность что воздух над этим стулом преобразуется в прекрасную девушку, она полюбит меня и мы будем счастливы.
    -Но тут полно одиноких девушек, почему бы вам не угостить одну из них порцией мороженного, и возможно из этого что-то выйдет.
    -Да, но какова вероятность?

capt99
08.10.2018 07:13
#19204091
По пути наименьшего сопротивления(с) всплыло сразу в голове.

expertykt
08.10.2018 07:14
#19204093
ПНД разве не одна из интерпретаций закона сохранения энергии? Т.е. в буквальном смысле это один из способов математической записи этого закона. Вроде бы этот основополагающий вопрос не раскрыт.
1. andrew526d Автор
  08.10.2018 07:20
  #19204109
  ПНД не один из способов математической записи закона сохранения энергии. Например, если внешнее поле меняется со временем, то полная энергия тела в этом поле может не сохраняться, тем не менее, двигаться оно будет в соответствии с ПНД.
  Хотя, действительно, есть очень тесная связь между ПНД и законом сохранения энергии, которую я здесь не раскрывал совершенно. Оставил это для будущих частей.
  1. expertykt
    08.10.2018 08:01
    #19204203
    Есть мнение, что незнание закона не исключает его действия.
1. caballero
  08.10.2018 11:57
  #19205065
  скорее интерпретация закона сохранения импульса. закон сохранения энергии демонстрируется в гамильтоновой версии механики
  1. expertykt
    09.10.2018 04:25
    #19207959
    Это только в случае, если в вашей вселенной закон сохранения импульса существует отдельно от закона сохранения энергии. Для справки: wp.wiki-wiki.ru/wp/index.php/%D0%9B%D0%B0%D0%B3%D1%80%D0%B0%D0%BD%D0%B6%D0%B5%D0%B2%D0%B0_%D0%BC%D0%B5%D1%85%D0%B0%D0%BD%D0%B8%D0%BA%D0%B0#.D0.97.D0.B0.D0.BA.D0.BE.D0.BD_.D1.81.D0.BE.D1.85.D1.80.D0.B0.D0.BD.D0.B5.D0.BD.D0.B8.D1.8F_.D1.8D.D0.BD.D0.B5.D1.80.D0.B3.D0.B8.D0.B8
    
    caballero
    09.10.2018 13:22
    #19209635
    закон сохранения энергии напрямую никак не связан с законом сохранения импульса. Закон сохранения энергии математически вытекает из глобальной симметрии по времени а закон сохранения импульса из симметрии по координатам. Ну или как сказно по ссылке, изотропности.
    
    expertykt
    10.10.2018 03:49
    #19212689
    Отсутствие прямой связи предполагает возможность несохранения энергии при сохранении импульса и наоборот.
    
    caballero
    10.10.2018 10:52
    #19213527
    так и было бы в случае неизотропности пространства или времени. Но изотропность пространства не связана напрямую с изотропностью времени.
    кроме того законы сохранения импульса и энергии нарушаются например при неопределенности Гейзенберга. Причем каждый по отдельности потому как опять же энергия связана с временем а импульс с координатами.
1. Tyusha
  08.10.2018 12:22
  #19205173
  ПНД не является законом сохранения ни энергии, ни импульса, ни чего бы то ни было другого, ни по форме, ни по смыслу тчк
  1. expertykt
    09.10.2018 04:24
    #19207957
    Укажите пожалуйста ошибки формы и смысла в этой записи закона сохранения энергии через лагранжиан. wp.wiki-wiki.ru/wp/index.php/%D0%9B%D0%B0%D0%B3%D1%80%D0%B0%D0%BD%D0%B6%D0%B5%D0%B2%D0%B0_%D0%BC%D0%B5%D1%85%D0%B0%D0%BD%D0%B8%D0%BA%D0%B0#.D0.97.D0.B0.D0.BA.D0.BE.D0.BD_.D1.81.D0.BE.D1.85.D1.80.D0.B0.D0.BD.D0.B5.D0.BD.D0.B8.D1.8F_.D1.8D.D0.BD.D0.B5.D1.80.D0.B3.D0.B8.D0.B8
    
    Tyusha
    09.10.2018 15:13
    #19210169
    «В огороде бузина, а в Киеве дядька».
    
    Как связаны законы сохранения и ПНД? Тем, что и там, и там запись выполнена с использованием лагранжиана?
    
    expertykt
    10.10.2018 03:40
    #19212681
    С одной стороны (формальной), лагранжиан это математическая запись ПНД. Поэтому приравнивание энергии к функции от ПНД очевидно указывает, что ПНД является основным принципом закона. С другой стороны (понятийной), смысл ПНД как инструмента вариационного исчисления заключается в отыскании такого уравнения движения, при котором энергия сохраняется.
1. gks
  09.10.2018 17:49
  #19210851
  Из ПНД следует закон сохранения энергии, при условии, что функция Лагранжа не зависит от времени. Если функция не зависит от координаты следует закон сохранения импульса. А если функция изотропна, то есть не зависит от направления, то следует закон сохранения момента импульса. Это более мощное утверждение, чем закон сохранения энергии.

Panzerschrek
08.10.2018 07:14
#19204095
Такое впечатление, что природа таинственным образом перебирает все возможные пути движения системы и выбирает из них самый лучший

А нет ли более материалистического объяснения вышеизложенного принципа?
1. caballero
  08.10.2018 12:11
  #19205115
  это принцип квантово механики. А там нет ничего материалистичного в смысле привычных нам из повседневного опыта понятий
  1. totally_nameless
    09.10.2018 05:10
    #19207985
    Не путайте людей. ПНД был сформулирован задолго до квантовой механики.
    
    caballero
    09.10.2018 13:16
    #19209595
    да, но движение по многим траекториям хорошо наблюдается именно в квантовой механике. В первую очередь в эксперименте с двумя щелями. в случае макрообьектов траектории практически сливаются.
    
    Tyusha
    09.10.2018 15:17
    #19210179
    Никогда ещё вы не были так близки к открытию феймановской формулировки квантовой механики.
1. expertykt
  09.10.2018 04:37
  #19207971
  Это не принцип, а впечатление конкретного человека. Принципа такого нет и объяснять здесь нечего.

LAG_LAGbI4
08.10.2018 07:57
#19204197
Я вообще ничего не понял.
1. Почему угол отражения равен углу падения. Что за бред про свет, который знает куда ему нужно попасть и заранее выбирает направление?
2. Почему расход топлива зависит от скорости?
3. Какое применение эта машинка имеет в реальном мире
1. saaivs
  08.10.2018 13:02
  #19205381
  Что за бред про свет, который знает куда ему нужно попасть и заранее выбирает направление?
  
  Свет не знает куда надо попасть. Ему все равно. Он просто распостраняется в соответствии с законами физики. А вот место куда он попадает — автоматически и оказывается «куда надо». Просто мы видим «задачу задом наперед» — мы видим что происходит в реальном мире, а теперь пытаемся найти строгое математическое и логическое обоснование того, почему оно происходит так, а не иначе.
  
  Почему расход топлива зависит от скорости?
  
  Если теория относительности не врет, то E=mc2. Поскольку скорость есть, разновидность энергии, то с увеличением скорости масса тела возрастает. Для дальнейшего изменения скорости(или поддержания скорости при наличии сопротивления среды, которая стремится уменьшить скорость тела) нужна энергия. Чем больше масса тела, тем больше энергии нужно чтоб его еще ускорить. т.е. чем выше скорость, тем больше энергии нужно(выше расход топлива), чтоб она стала еще больше. Вот и выходит в итоге, что расход зависит от скорости в общем случае.
  1. expertykt
    09.10.2018 04:33
    #19207967
    Лагранжиан не учитывает релятивистские эффекты, поэтому пример с ростом массы от скорости неуместен в принципе.
    
    Tyusha
    09.10.2018 15:21
    #19210199
    Что мешает записать другой лагранжиан, релятивистский!?
    
    expertykt
    10.10.2018 03:13
    #19212651
    Вы правы, речь не о применимости лагранжиана к релятивистскому случаю, а о применимости релятивистского случая для иллюстрации зависимости энергии от квадрата скорости в классическом случае.

michael_vostrikov
08.10.2018 08:06
#19204211
-1
Ну мне кажется с фонариком правильнее будет вот так. Наблюдатели в точках X и Y тоже его увидят. Миллион лучей выглядят уже не так таинственно)
1. SwingoPingo
  08.10.2018 08:29
  #19204267
  +1
  Таинственным выглядит то, что миллион наблюдателей увидят только те фотоны от источника А, которые до них дошли в соответствии с принципом ПНД.
  1. michael_vostrikov
    08.10.2018 10:32
    #19204685
    +1
    Ну так это потому что другие фотоны в другую сторону летят, разве нет? Я говорил не про миллион наблюдателей, а про миллион лучей, хоть один да пойдет в сторону наблюдателя. ПНД это следствие, а не причина.
    
    8street
    08.10.2018 10:49
    #19204751
    Вот тут и я согласен. Фонарь не выпускает один фотон, чтобы он попал в наблюдателя. Он выпускает их очень много, в разные стороны. А вот почему они летят прямолинейно — это уже другой вопрос. У меня есть мнение, что это из-за их нулевой массы (хотя некоторые считают что она не нулевая), просто согласно формуле F=ma. Другие силы просто не могут на них действовать.
    
    saaivs
    08.10.2018 12:41
    #19205291
    А вот почему они летят прямолинейно — это уже другой вопрос.
    
    Ну они летят не то чтобы «прямолинейно». Траектория их движения соответствует геодезическим линиям пространства. В условиях сильной гравитации (см. гравитационное линзирование) их траектория может быть весьма причудлива. Хотя по «их собственному мнению» да, они будут двигаться «по прямой». Но так и время их жизни, «по собственному мнению», равно нулю, в силу того, что двигаются со скоростью «c». А если говорить еще обстоятельней, то говорить о конкретной траектории движения элементарных частиц можно с некоторой натяжкой. Есть менее, и более вероятные пути их движения, которые в момент наблюдения просто коллапсируют в конкретные значения. Что позволяет считать, что они движутся по всем возможным путям причем одновременно (см. интеграл по траекториям, сформулированный Р. Фейнманом).
    
    extempl
    08.10.2018 14:29
    #19205747
    А вот мне тоже интересно, как это так "свет идёт именно этим (кратчайшим) путём а не любым другим".
    
    Фотоны выпускаются во все стороны
    
    Фотоны летят во все стороны с постоянной (для среды) скоростью
    
    К некоторой точке фотоны летевшие путём A долетают быстрее
    
    К этой же точке чуть позже прилетают другие фотоны летевшие путём B.
    
    То есть если закрыть путь A, то свет всё-равно появится в точке. И если будут открыты оба — суммарно там будет светлее.
    Почему же всё-таки говорится, что "выбирает кратчайший путь?" Выбирает все пути, просто по какому-то (очевидно, кратчайшему) долетает быстрее.
    Так в чём же тут мистика?
    
    khim
    08.10.2018 20:05
    #19207067
    То есть если закрыть путь A, то свет всё-равно появится в точке.
    Вы когда-нибудь солнечные зонтики видели? В том-то и дело, что он не появится.
    
    extempl
    08.10.2018 20:07
    #19207077
    Он — кто? Конкретный пучок фотонов или свет в принципе? Отражённый от других предметов разве не появится?
    
    khim
    08.10.2018 20:19
    #19207123
    Свет от конкретного источника. Да, если есть другие предметы, то что-то может и дойти. Он может вообще двигаться по очень разным путям. Может даже дойти несколько лучей от одного источника к одному приёмнику. Но они всегда будут двигаться по траектории, соответствующей ПНД.
    
    Alexander_vrn
    09.10.2018 07:11
    #19208103
    Проблема с нулевой массой как раз легко обходится той же самой формулой, но в импульсной форме, т.е. F=dp/dt. А с импульсом у фотона все ОК.
  1. dimm_ddr
    08.10.2018 15:24
    #19206009
    Если бы фотон отражался не по принципу «угол падения равен углу отражения», то он все равно прошел бы минимально возможный путь, но оказался бы в другом месте. А в указанных точках оказались бы другие фотоны.

michael_vostrikov
08.10.2018 11:09
#19204835
Аппарат получился таким, что выработка топлива точно равна mgh
Вопрос к знающим людям. Говорят, что при падении потенциальная энергия переходит в кинетическую, и закон сохранения энергии не нарушается.

Какова потенциальная энергия у этого камня? Не может же у него быть 2 потенциальных энергии. Откуда при падении берется кинетическая энергия? Как здесь правильно рассуждать?
1. Tsvetik
  08.10.2018 11:12
  #19204857
  Я считаю, что у этого шарика потенциальная энергия 77. На самом деле это не важно какая именно. Важно, что она сохраняется.
1. caballero
  08.10.2018 12:05
  #19205089
  потенциальная энергия — это всегда разность. Понятие потенциала в какой то точке не имеет смысла.
1. SwingoPingo
  08.10.2018 14:59
  #19205909
  Можно так трактовать: потенциально получаемая кинетическая энергия. Энергия, которая может быть получена в результате воздействия на тело действующих на него в этой точке пространства сил. Она относительна. Кинетическая энергия это опять же работа, которую совершает тело до полной (относительно начала координат скорости) остановки. Конечно присутствует некий элемент диалектики.
1. ixamilion
  08.10.2018 16:08
  #19206201
  Потенциальный значит возможный.
  Потенциальная энергия — такое количество энергии, которое возможно преобразовать, например, в кинетическую.
  Т.о. потенциальная энергия просто алгебраическая абстракция, помогающая получить более конкретные показатели, например скорость в точке, если тело массой m упадет с высоты h
  
  Возвращаясь к вашему вопросу. Если вы ставите 2 задачи возможного (потенциального) падения, то и потенциальных энергий у тела будет 2.
  1. michael_vostrikov
    08.10.2018 16:36
    #19206313
    А откуда берется реальная кинетическая энергия, которая делает работу?
    
    cuwHuk
    08.10.2018 23:05
    #19207527
    Гравитация. А откуда берется гравитация на сегодняшний день, надо полагать, не знает никто.
1. Howru
  09.10.2018 07:11
  #19208105
  Правильно рассуждать так: Потенциальная энергия существует только в каком-то поле.
  
  Если этот камень находится где-то в глубинах космоса, то у него её просто нет.
  Если же на Земле — то разница между координатами камня и центра Земли.
  1. michael_vostrikov
    09.10.2018 08:55
    #19208283
    Допустим, он прилетел из глубин космоса в поле Земли и упал на нее. Откуда у него взялась энергия, которая произвела разрушения в месте падения?
    
    Howru
    09.10.2018 12:09
    #19209207
    Все эти ответы есть в определении потенциальной энергии.
    
    >Потенциальная энергия — скалярная физическая величина, представляющая собой часть полной механической энергии системы, находящейся в поле консервативных сил. Зависит от положения материальных точек, составляющих систему, и характеризует работу, совершаемую полем при их перемещении.
    
    Камень перемещается в гравитационном поле Земли — значит теряет потенциальную энергию, которая превращается в кинетическую.
    
    Попробую объяснить с лифтом. Когда человек стоит на земле, он уже обладает потенциальной энергией (т.к. находится на расстоянии 6000 км от гравитационного центра системы). Но примем это нулем, как нашу точку отсчета.
    
    Человек заходит в лифт и едет на 10-ть этажей вверх. Лифт совершает работу по перемещению груза в гравитационном поле, а значит увеличивает потенциальную энергию. На 10-м этаже у человека есть некоторое количество потенциальной энергии.
    Она называется потенциальной потому что ее наличие не видно сразу в нашем человеческом смысле. Чтобы ее увидеть, надо выйти в окно, и вот тогда потенциальная энергия начнет быстро превращаться в кинетическую.
    
    Тут есть несколько уловок, чтобы упростить формулы. Потенциальная энергия бесконечно удаленных тел считается равна нулю. Поэтому пока камень находится очень далеко от Земли — у него нет потенциальной энергии (в системе Земля-камень). Когда он приближается, его потенциальная энергия растет. (Тут правда другая проблема, когда центры масс Земли и камня совпадут, потенциальная энергия станет бесконечной :).
    Но т.к. нас всегда интересует не само значение потенциальной энергии, а разница между двумя разными значениями, то все это не имеет значения.
    Объект поменял свое положение в системе — изменилась его потенциальная энергия.
    
    michael_vostrikov
    09.10.2018 12:27
    #19209301
    Когда он приближается, его потенциальная энергия растет
    Но когда он падает с горы, он тоже приближается, но потенциальная энергия падает. Тут какое-то противоречие.
    
    Druu
    09.10.2018 20:38
    #19211479
    Когда бесконечно удаленный камень приближается, то его энергия не растет, т.к. на камень не действуют никакие силы. Сколько бы вы ни приближали бесконечно удаленный камень, он так и останется бесконечно удаленным :)
    
    michael_vostrikov
    09.10.2018 20:52
    #19211517
    Бесконечно удаленных камней в природе не бывает. Да и спрашивал я не про них.
    
    Howru
    10.10.2018 12:13
    #19213929
    Тут противоречие в том что мы используем разные формулы.
    Вы используете упрощенную формулу в поле тяготения Земли вблизи поверхности.
    Та самая Е=mgh. По ней в центре Земли энергия будет ноль, на бесконечном расстоянии — бесконечность.
    Эта формула удобна для расчетов на Земле, компактна и красива.
    
    Я-же пользуюсь формулой гравитационного потенциала для точечной массы и произвольного тела. И вот там все наоборот — на бесконечности ноль, в центре масс — бесконечность.
    
    Но т.к. абсолютное значение потенциальной энергии никого не интересует, а интересует только разность энергии при перемещении между двумя точками — обе формулы дадут одинаковое число для этой самой разности.
1. Druu
  09.10.2018 07:22
  #19208121
  Какова потенциальная энергия у этого камня?
  Ноль.
  
  Не может же у него быть 2 потенциальных энергии.
  Не может, просто ноль и все.
  
  Откуда при падении берется кинетическая энергия?
  Ниоткуда, ведь шарик на месте стоит, а не падает.
  1. michael_vostrikov
    09.10.2018 08:50
    #19208279
    Шарик при падении не падает?) Ну ок.
    
    Druu
    09.10.2018 10:11
    #19208535
    Так на картинке нет никакого падения :)
    Он просто стоит на связи и не двигается.
    Вот если вы добавите еще какие-нибудь силы (например, от какого-то бокового ветра) то будет уже другой разговор.
    
    michael_vostrikov
    09.10.2018 12:24
    #19209277
    На статической картинке его и не может быть, падение описано словами в сопровождающей фразе.
    Ну допустим я его переместил горизонтально на несколько сантиметров. А дальше что, откуда реальная энергия берется?
    
    Druu
    09.10.2018 20:44
    #19211493
    Ну допустим я его переместил горизонтально на несколько сантиметров. А дальше что, откуда реальная энергия берется?
    Если передвинете — то будет энергия 0, при падении камня она начнет уменьшаться до, например, -42 (когда камень упал на дно).
    При этом сама по себе отрицательная потенциальная энергия не является какой-либо проблемой (с физико-математической точки зрения), но обычно это просто неудобно. По-этому мы уровень дна примем за 0, а тот уровень, на котором камень был изначально — станет, с-но, 42.
    
    Иными словами — чтобы определить потенциальную энергию состояния системы вам надо сперва выбрать некоторое состояние и объявить его нулевым. До тех пор — потенциальная энергия не определена.
    Как выбирается нулевое состояние? Абсолютно произвольно. Как вам удобно в данной задаче — так и выбираете. Этот выбор ровным счетом ни на что не влияет кроме вашего удобства, никакого физического смысла за ним не стоит.
    
    michael_vostrikov
    09.10.2018 21:04
    #19211587
    Ну я спрашиваю про сами физические процессы, а не про их обозначения. Что там реально происходит, вплоть до отдельных частиц и квантов энергии. Кинетическая энергия падающего камня это объективная вещь, которая производит объективные изменения. Объективные вещи не появляются из произвольных обозначений.
1. gks
  09.10.2018 19:00
  #19211089
  На данном рисунке потенциальная энергия равно 0, кинетическая тоже 0. Так как на камень действует сила реакции опоры. Камень покоиться на вершине. Если он начнет падать, то на него будет действовать сила mg. m*a = mg = F.
  m*dv/dt = F
  Если мы домножим уравнение справа и слева на пройденный путь падения
  m*dv *dl/d*t = F*dl
  dl/dt = v
  то получим m*v *(dv) = F*dl
  
  далее m*d(v^2/2) = F*dl
  Обзовем левую часть кинетической энергией, правую элементарной работой
  Зная пройденное расстояние камня, мы можем посчитать как изменится кинетическая энергии
  dT = A
  Работа — это изменение кинетической энергии камня
  Зачем это все нужно? Уравнения движения — это дифференциальные уравнения. Вводя понятия потенциальной и кинетической энергии мы переходим от дифференциальных к алгебраическим уравнениям.
  Далее развиваем мысль. Что работа A состоит из двух частей, работы центральных сил, Aц + работа не центральных (а ля трения) Aнц
  Работа центральный сил — это и есть обратное изменения потенциальной энергии
  Aц = -dU
  dT = -dU + Aнц
  dT + dU = Aнц
  d(T + U) = Aнц
  T+U — сумма потенциальной и кинетической энергии — полная энергия системы
  Изменение полной энергии идет на работу нецентральных сил
  Соответственно, если в системе нет нецентральных сил, то разница полной энергии системы равно 0. Это закон сохранения энергии.
  Зачем отделять центральную от нецентральной силы. Ответ простой, что для центральной силы сумма F(l) *dl равна разнице некой функции U(l) — U(l + dl). Для гравитации -(m*g*l — m*g*(l + dl)) мы можем выделить функцию U(l) = -m*g*l
  в итоге получаем, закон сохранения энергии
  d(m*v^2/2 — m*g*l) = работе нецентральных сил = 0
  А это уже легко можно применять для решения практических задач
  Посчитать с какой скоростью упадет камень справа с высоты h2 и слева c высоты h1
  1. michael_vostrikov
    09.10.2018 20:20
    #19211393
    На данном рисунке потенциальная энергия равно 0, кинетическая тоже 0. Так как на камень действует сила реакции опоры.
    Разве потенциальная энергия появляется только когда камень начинает падать? Это как-то странно. Он может например почву продавливать, пока лежит, то есть тоже совершает работу, значит возможность для ее совершения создается постоянно.
    
    С рисунком я начинаю понимать, там одна высота h от центра Земли. Но пока непонятно, как это связать с равномерно летящим в космосе камнем.
    
    Правильно ли говорить, что энергию камню сообщает поле?
    
    gks
    09.10.2018 23:12
    #19212115
    Я выше описал. Что потенциальной энергией не камень обладает — это правило вычисления работы центральных сил. В нашем случае гравитации. Если центральная сила не перемещает предмет, то его работа равна нулю. То что говорят, что предмет обладает потенциальной энергией — это удобный жаргонизм. Чтоб рассматривать замкнутую систему камня (T + U), которая сохраняется в отсутствии нецентральных сил. Оно с одной стороны упрощает (позволяет решать типовые задачи не думая), а с дугой запутывает. Основная цель всего этого — это перевести дифференциальные уравнения в алгебраические. И считать это все на коленках.
    Если камень продавливает землю, то работу совершает сила гравитации и она равна mg*dl, где dl — это глубина продавливания. Если на момент начала наблюдения и конца, скорость лежащего камня равна нулю или ей можно пренебречь, то можно сказать, что вся работа гравитации ушла на преодоление работы силы трения почвы. И эта работа равна mg*dl
    
    Правильно ли говорить, что энергию камню сообщает поле?
    
    Что такое поле — это функция силы F(q) в некоторой точке q действующей на тело. Fg ~ m1*m2/r^2, где r — это расстояние между центрами масс двух тел. Для удобства можно слабо меняющуюся часть обозначить Eg = G*M/R^2, тогда другое мелкое тело на поверхности большого будет испытывать на себе силу Fg = m*Eg. Eg — мы знаем просто как g, ускорение свободного падения.
    А что такое сила? А сила — это есть скорость изменения количества движения (импульса). Это определение. Это не закон. То есть поле — это как меняется импульс тела в единицу времени в заданной точке пространства. Если импульс (количество движения) не меняется, то на тело не действует сила.
    Энергия это способность изменять движение тела, поле это сила (тоже способность менять движения тела) действующая на тело. Поэтому фраза
    энергию камню сообщает поле
    — это масло масленое. Говорить правильно, но это ничего не дает.
    Более точное выражение, что поле (нечто создающее силу в точке пространства) совершает работу над телом. И эта работа заключается в изменении кинетической энергии тела. Таких нечто известно не так много, всего 4 штуки. Вот как они это делают, это загадка природы. Гравитация и кулоновская — это центральные силы (зависят от расстояния между телами).
    Можно подойти к задачи с другого бока и сказать, что нет никаких полей, а тела искривляют пространство, делают вмятины в которых сами находятся, и затягивают другие тела. По принципу матраса, если на него положить большой камень, то будет большая вмятина, и если класть рядом мелкие камни, то они будут в эту вмятину скатываться. И можно сказать что большой камень притягивает мелкий. Но это тоже не отвечает на вопрос, как камень создает вмятины в пространстве. Но если знать, что один и тот же камень создает одинаковую вмятину, то эту абстракцию можно также использовать для расчета движения траектории более мелкого камня. И тогда к задаче можно подойти сугубо геометрически.

Tsvetik
08.10.2018 11:11
#19204849
Когда участвовал в MiniAICup №2 с амебами, то попытался применить ПНД в этой игре. Почитал про задачу наискорейшего спуска, понял, что такое этот Лагранжиан и попытался применить эти знания на практике. Всего-лишь найти минимальную по времени траекторию, которая позволит амебе съесть еду на карте. Для одной точки еды вроде-бы еще что-то получалось, но когда еды много, уравнения получались совершенно неописуемыми.
Сделал вывод, что Лагранжиан применим только для расчета простых теоретических задач, а прикладные им не решаются.
Может, я что-то делал не так?

V-core
08.10.2018 11:37
#19204977
Прошло 20 лет после написания рассказа «История твоей жизни» (англ. Story of Your Life) американским писателем Тедом Чаном.
Повесть рассказывает о женщине-лингвисте, изучающей язык пришельцев и благодаря проникновению в их картину мира построенной на базе того что в математике и физике основополагающим для них является принципа Ферма, она понимает, что мышление пришельцев устроено принципиально иначе. Для них не существует свободы выбора и причинно-следственной связи, поскольку они воспринимают историю не как последовательность, а в целостности, как совокупность всех уже бывших и ещё только предстоящих фактов. Изучив этот язык Она осознает всю свою жизнь целиком.
В 2016 на экраны выходит снятый по этом рассказу научно-фантастический фильм «Прибытие».
В 2018 на Хабре появляется статья.
1. Wizard_of_light
  08.10.2018 15:20
  #19205985
  Я эту историю воспринял как описание информационной атаки инопланетян, которые скинули наивным землянам комплекс подчиняюще-программирующих мемов под видом языка и свалили в туман, потирая щупальца.
  1. V-core
    09.10.2018 10:56
    #19208757
    Прекрасная идея для 2 части.
    Через N лет просветленое человечество, знающее свою судьбу, принимает приход щупалец и делает осознанный выбор о необходимости, например, самовыпилиться. Лишь дебилы с линейно-квантовым мышлением могут противостоять судьбе и физике. :)
1. DjSapsan
  08.10.2018 16:32
  #19206293
  А в итоге в фильме слили идею и превратили в твист «передача информации из будущего в прошлое» и добровольный выбор страданий дочери. В оригинале же героиня видела свой будущий выбор. Именно свой выбор. Она не могла выбрать что-то другое.
  П.С. часть рассказа посвящена именно сабжу

fragile
08.10.2018 12:06
#19205095
-1
Со времен Галилея было известно, что тела, на которые не действуют никакие силы, двигаются по прямым линиям, то есть по кратчайшему пути.

Если на тела не действуют никакие силы, то тела вообще ни по какому пути не двигаются.
1. Tyusha
  08.10.2018 12:13
  #19205123
  Это вам к Аристотелю.
1. saaivs
  08.10.2018 13:13
  #19205423
  Равномерное и прямолиненйное движение по геодезическим линиям(движение по инерции) пространства не в счет?
  1. totally_nameless
    08.10.2018 22:44
    #19207479
    В счет :) только оно неотличимо от состояния покоя…
    sarcasm>Может это и имелось ввиду?</sarcasm
1. CMTV
  09.10.2018 07:12
  #19208107
  Если на тела не действуют никакие силы, то тела вообще ни по какому пути не двигаются.
  
  А как же вариант, когда они исходя из начальных условий имеют скорость?)

saaivs
08.10.2018 13:09
#19205407
Например, возьмем шарик и поместим его в пустое пространство. На некотором отдалении от него поставим упругую стенку. Допустим, мы хотим, чтобы через некоторое время шарик оказался в том же самом месте.

Наверное, все-таки не в в пустое, а в некоторое пространство с постоянным сопротивлением среды в любой точке независимо от направления. Иначе какая-то энергия, переданной шарику, давже в случае не идеально упругого удара о станку так и останется с ним, и никаких причин останавливаться в начальной точке у него не будет в этой вселенной.
1. andrew526d Автор
  08.10.2018 20:42
  #19207179
  А он и не должен останавливаться в конечной точке. Он должен там оказаться в конечный момент времени, т. е. пролететь через конечную точку в нужный момент времени. А дальше пусть себе летит.

Tomasina
08.10.2018 13:26
#19205497
Плчему тогда самолеты летают по дуге, а не по прямой? Я имею в виду не высоту, а маршрут.
1. Ktulhy
  08.10.2018 14:36
  #19205785
  Там дело в том, что земля сферическая (с натяжкой).
  Простой ответ — почему земля круглая, а карта прямоугольная?)
1. Peacemaker
  08.10.2018 15:02
  #19205919
  Потому что на поверхности шара кратчайшее расстояние — это геодезическая линия. Прямой она будет выглядеть, только если смотреть на неё из плоскости, задаваемой точками А, Б (начало и конец маршрута), и О — центром шара. Со всех остальных точек — дуга.

DimPal
08.10.2018 13:49
#19205589
Наверно придираюсь к словам, но… Статья называется «Принцип наименьшего действия», а рассматриваемые случаи скорее относятся к «принципам бездействия движущихся тел в инерциальных системах отсчета». Угол падения равен углу отражения работает для «сферических коней в вакууме», бросьте кубик в стену — угол отражения будет зависеть от ориентации кубика в момент касания стены, от шероховатости стены, от коэффициента скольжения и т.д.

Daddy_Cool
09.10.2018 00:16
#19207679
Тоже размышлял насчет принципа.
Насколько я помню/понимаю, теорема Нетёр выводится именно из этого принципа. Но говорит ли это что-нибудь о природе/происхождении принципа?

nmrulin
09.10.2018 07:14
#19208111
Принцип наименьшего действия выполняется, потому, что мы искуственно называем «действием», то, что будет принимать наименьшее значение, если будет подчиняться к примеру «законам Ньютона».
В частности эта подгонка видна в задаче про автомобиль «Выработка топлива прямо пропорциональна высоте, на которой в данный момент находится автомобиль.» -а не постоянна? Потому, что мы специально подгоняем условия, так чтобы работал принцип наименьшего действия.
Так что по мне — данный принцип это удобный математический аппарат, но не попытка (в отличие от законов Ньютона) объяснения «как всё устроено».

orange_10
09.10.2018 07:16
#19208117
Ох…

Мне кажется, вы только сильнее запутаете людей, которые не знают что такое ПНД. Все примеры, кроме первого, мне кажутся крайне неудачными, поскольку сформилированы в терминах задачи на оптимальное управление. И неудивительно, что вы используете именно их, т.к. и оптимальное управление, и ПНД формулируются в одинаковых математических терминах, а именно как задачи на вариации функционалов и поиска экстремумов. Заметьте, вы специально подбираете параметры «машины» так, чтобы функционал качества для задачи оптимального управления соответствовал функционалу действия. Что, как мне кажется, не сильно упрощает понятие ПНД.

Хотите объяснить «на пальцах» — начните с того, как из ПНД вывести первый закон Ньютона. Это просто, наглядно и требует абсолютного минимума математики.

grigorym
09.10.2018 08:20
#19208239
Статья капец какая вредная, потому что за счет использования неправильных слов делает всё только непонятнее, чем было. Моей работой является придумывать понятные объяснения, поэтому мой мозг взрывается в ярости каждый раз, когда я такое читаю (это мои извинения автору, авансом). Взять хотя бы вот эту картинку.

Автор говорит здесь про «световой луч», и у читающего возникает впечатление, что начальная траектория луча якобы магическим образом зависит от того, есть там стекло или нет, и где расположен детектор. Но разумеется, это полный бред, как и в случае с зеркалом выше. Начальная траектория луча (не трогаем квантовую механику и волновую функцию) зависит только и единственно от того, в каком направлении излучает фотоны фонарик.
Тут объяснять надо было совсем по-другому. Надо было спросить — если фонарик излучает фотоны во все стороны, то по какой траектории пройдет тот фотон, который попадет в детектор? И тогда уже показать, что это будет зеленая траектория, а не красная, и объяснять, почему.

О фразах вида «оказывается, более оптимально — немного набрать высоты, какое-то время там задержаться, выработав побольше топлива, а затем уже спуститься в точку В» я даже говорить не хочу.
1. aleksandros
  09.10.2018 08:47
  #19208271
  Насчёт второй части — про летающую машинку — действительно чуть запутанно. Если мы хотим переместить железный жарик с одного конца стола в другой, то самое оптимальное это его катнуть, но никак не подбрасывать в воздух. Это подсказывает здравый смысл. А вот если в столе «вырыть ямку» как раз с параболическим профилем, то шарик и толкать не надо. Достаточно подвести его к краю ямки и он сам докатиться до другого конца под действием силы тяжести.
1. Kriminalist
  09.10.2018 16:54
  #19210587
  Картинка вообще странная. Где точка входа луча в лист стекла и где точка выхода? Или у нас стекло нулевой толщины? Или точка В в толще стекла расположена? Так тогда красного луча вообще быть не может, переломится и не попадет в точку В.

Принцип наименьшего действия. Часть 1 +62

Предыстория

Свободное тело

В поле тяжести

Функция Лагранжа и принцип наименьшего действия

Не все так просто

Комментарии (155)

andrew526d Автор

andrew526d Автор

andrew526d Автор

andrew526d Автор

andrew526d Автор

andrew526d Автор

andrew526d Автор

andrew526d Автор

andrew526d Автор

andrew526d Автор

andrew526d Автор