Возникла потребность написать быстрое вычисление Sin и Cos. За основу для вычислений взял разложение по ряду Тейлора. Использую в 3D-системах (OpenGL и графическая библиотека своей разработки). К сожалению свести ряд «идеально» для Double не получается, но это компенсируется хорошим ускорением. Код написан на встроенном в Delphi XE6 ассемблере. Используется SSE2.
Для научных вычислений не подходит, а для использования в играх вполне.
Точности хватает, чтобы покрыть разрядность числа Single, которое используется
для умножения на матрицу.
В итоге:
- Достигнутая точность результата равна: 10.e-13
- Максимальное расхождение с CPU — 0.000000000000045.
- Скорость увеличена в сравнении с CPU в 4.75 раза.
- Скорость увеличена в сравнении с Math.Sin и Math.Cos в 2.6 раза.
Для теста использовал процессор Intel Core-i7 6950X Extreme 3.0 ГГц.
Исходный текст на Delphi встроен в комментарии к ассемблеру.
Исходный код:
var
gSinTab: array of Double;
gSinAddr: UInt64;
const
AbsMask64: UInt64 = ($7FFFFFFFFFFFFFFF);
PI90: Double = (PI / 2.0);
FSinTab: array[0..7] of Double =
(1.0 / 6.0, //3!
1.0 / 120.0, //5!
1.0 / 5040.0, //7!
1.0 / 362880.0, //9!
1.0 / 39916800.0, //11!
1.0 / 6227020800.0, //13!
1.0 / 1307674368000.0, //15!
1.0 / 355687428096000.0); //17!
//Максимумы функции Sin для положительных значений
QSinMaxP: array[0..3] of Double = (0.0, 1.0, 0.0, -1.0);
//Максимумы функции Sin для отрицательных значений
QSinMaxM: array[0..3] of Double = (0.0, -1.0, 0.0, 1.0);
//Знаки квадрантов для положительных значений
QSinSignP: array[0..3] of Double = (1.0, 1.0, -1.0, -1.0);
//Знаки квадрантов для отрицательных значений
QSinSignM: array[0..3] of Double = (-1.0, -1.0, 1.0, 1.0);
function Sinf(const A: Double): Double;
asm
.NOFRAME
// На входе A в xmm0
// Четверть окружности
// X := IntFMod(Abs(A), PI90, D);
// Result := FNum - (Trunc(FNum / FDen) * FDen);
pxor xmm3, xmm3
comisd A, xmm3
jnz @ANZ
ret // Result := 0.0;
@ANZ:
//Флаг отрицательного угла
//Minus := (A < 0.0);
setc cl
movsd xmm1, [AbsMask64] //Abs(A)
pand A, xmm1
movsd xmm1, [PI90] //PI90 = FDen
movsd xmm2, A //Копия A = FNum
divsd xmm2, xmm1 //(FNum / FDen)
roundsd xmm2, xmm2, 11b //11b - Trunc
cvtsd2si rax, xmm2 //Целая часть (X в EAX)
mulsd xmm2, xmm1
subsd xmm0, xmm2
//-----------------------------------
//Нормализация квадранта
and rax, 3 // D := (D and 3);
//-----------------------------------
// Проверка на максимум функции
// if (X = 0.0) then
// begin
// if Minus then
// Exit(QSinMaxM[D]) else
// Exit(QSinMaxP[D]);
// end;
comisd xmm0, xmm3
jnz @XNZ
shl rax, 3 //умножить номер квадранта на размер Double (8 байт)
cmp cl, 1 //Если угол отрицательынй, то переход
je @MaxMinus
@MaxPlus:
lea rdx, qword ptr [QSinMaxP]
movsd xmm0, qword ptr [rdx + rax]
ret
@MaxMinus:
lea rdx, qword ptr [QSinMaxM]
movsd xmm0, qword ptr [rdx + rax]
ret
//-----------------------------------
@XNZ:
//При нечетном квадранте нужно вычесть градусы для симметрии
// if (D and 1) <> 0 then X := (PI90 - X);
mov edx, eax
and edx, 1
cmp edx, 0
je @DZ
subsd xmm1, xmm0
movsd xmm0, xmm1
//-----------------------------------
@DZ:
// Result остается в xmm0
// X в xmm0
// N := (X * X) в xmm2
// F := (N * X) в xmm1
// N
movsd xmm2, xmm0 // Копия X
mulsd xmm2, xmm2 // N := (X * X)
// F
movsd xmm1, xmm2 // Копия N
mulsd xmm1, xmm0 // F := (N * X)
//Загружаем таблицу факториалов для синуса
mov rdx, [gSinTab]
movaps xmm4, dqword ptr [rdx]
movaps xmm6, dqword ptr [rdx + 16]
movaps xmm8, dqword ptr [rdx + 32]
movaps xmm10, dqword ptr [rdx + 48]
//Извлекаем нечетную часть таблицы
movhlps xmm5, xmm4
movhlps xmm7, xmm6
movhlps xmm9, xmm8
movhlps xmm11, xmm10
// Result := X - F * PDouble(gSinAddr)^;
mulsd xmm4, xmm1 //FSinTab[0]
subsd xmm0, xmm4
// F := (F * N);
// Result := Result + F * PDouble(gSinAddr + 8)^;
mulsd xmm1, xmm2
mulsd xmm5, xmm1 //FSinTab[1]
addsd xmm0, xmm5
// F := (F * N);
// Result := Result - F * PDouble(gSinAddr + 16)^;
mulsd xmm1, xmm2
mulsd xmm6, xmm1 //FSinTab[2]
subsd xmm0, xmm6
// F := (F * N);
// Result := Result + F * PDouble(gSinAddr + 24)^;
mulsd xmm1, xmm2
mulsd xmm7, xmm1 //FSinTab[3]
addsd xmm0, xmm7
// F := (F * N);
// Result := Result - F * PDouble(gSinAddr + 32)^;
mulsd xmm1, xmm2
mulsd xmm8, xmm1 //FSinTab[4]
subsd xmm0, xmm8
// F := (F * N);
// Result := Result + F * PDouble(gSinAddr + 40)^;
mulsd xmm1, xmm2
mulsd xmm9, xmm1 //FSinTab[5]
addsd xmm0, xmm9
// F := (F * N);
// Result := Result - F * PDouble(gSinAddr + 48)^;
mulsd xmm1, xmm2
mulsd xmm10, xmm1 //FSinTab[6]
subsd xmm0, xmm10
// F := (F * N);
// Result := Result + F * PDouble(gSinAddr + 56)^;
mulsd xmm1, xmm2
mulsd xmm11, xmm1 //FSinTab[7]
addsd xmm0, xmm11
//-----------------------------------
// if Minus then
// Result := (Result * QSinSignM[D]) else
// Result := (Result * QSinSignP[D]);
shl rax, 3 //Умножаем на 8
cmp cl, 1
je @Minus
lea rdx, qword ptr [QSinSignP]
mulsd xmm0, qword ptr [rdx + rax]
ret
@Minus:
lea rdx, qword ptr [QSinSignM]
mulsd xmm0, qword ptr [rdx + rax]
end;
//------------------------------------
function Cosf(const A: Double): Double;
asm
.NOFRAME
// A в xmm0
// Четверть окружности
// X := IntFMod(AMod, PI90, D);
// Result := FNum - (Trunc(FNum / FDen) * FDen);
pxor xmm3, xmm3
comisd A, xmm3
jnz @ANZ
movsd xmm0, [DoubleOne]
ret // Result := 1.0;
//-----------------------------------
@ANZ:
//Флаг отрицательного угла
//Minus := (A < 0.0);
setc cl
movsd xmm1, [AbsMask64] //Abs(A)
pand A, xmm1
//-----------------------------------
movsd xmm1, [PI90] //PI90 = FDen
//-----------------------------------
// if Minus then
// AMod := Abs(A) - PI90 else
// AMod := Abs(A) + PI90;
cmp cl, 1
je @SubPI90
addsd A, xmm1
jmp @IntFMod
@SubPI90:
subsd A, xmm1
//-----------------------------------
@IntFMod:
movsd xmm2, A //Копия A = FNum
divsd xmm2, xmm1 //(FNum / FDen)
roundsd xmm2, xmm2, 11b //11b - Trunc
cvtsd2si rax, xmm2 //Целая часть (X в EAX)
mulsd xmm2, xmm1
subsd xmm0, xmm2
//-----------------------------------
//Нормализация квадранта
and rax, 3 // D := (D and 3);
//-----------------------------------
// Проверка на максимум функции
// if (X = 0.0) then
// begin
// if Minus then
// Exit(QSinMaxM[D]) else
// Exit(QSinMaxP[D]);
// end;
comisd xmm0, xmm3
jnz @XNZ
shl rax, 3 //умножить номер квадранта на размер Double (8 байт)
cmp cl, 1 //Если угол отрицательынй, то переход
je @MaxMinus
@MaxPlus:
lea rdx, qword ptr [QSinMaxP]
movsd xmm0, qword ptr [rdx + rax]
ret
@MaxMinus:
lea rdx, qword ptr [QSinMaxM]
movsd xmm0, qword ptr [rdx + rax]
ret
//-----------------------------------
@XNZ:
//При нечетном квадранте нужно вычесть градусы для симметрии
// if (D and 1) <> 0 then X := (PI90 - X);
mov edx, eax
and edx, 1
cmp edx, 0
je @DZ
subsd xmm1, xmm0
movsd xmm0, xmm1
@DZ:
// Result остается в xmm0
// X в xmm0
// N := (X * X) в xmm2
// F := (N * X) в xmm1
// N
movsd xmm2, xmm0 // Копия X
mulsd xmm2, xmm2 // N := (X * X)
// F
movsd xmm1, xmm2 // Копия N
mulsd xmm1, xmm0 // F := (N * X)
//Загружаем таблицу факториалов для синуса
mov rdx, [gSinTab]
movaps xmm4, dqword ptr [rdx]
movaps xmm6, dqword ptr [rdx + 16]
movaps xmm8, dqword ptr [rdx + 32]
movaps xmm10, dqword ptr [rdx + 48]
//Извлекаем нечетную часть таблицы
movhlps xmm5, xmm4
movhlps xmm7, xmm6
movhlps xmm9, xmm8
movhlps xmm11, xmm10
// Result := X - F * PDouble(gSinAddr)^;
mulsd xmm4, xmm1 //FSinTab[0]
subsd xmm0, xmm4
// F := (F * N);
// Result := Result + F * PDouble(gSinAddr + 8)^;
mulsd xmm1, xmm2
mulsd xmm5, xmm1 //FSinTab[1]
addsd xmm0, xmm5
// F := (F * N);
// Result := Result - F * PDouble(gSinAddr + 16)^;
mulsd xmm1, xmm2
mulsd xmm6, xmm1 //FSinTab[2]
subsd xmm0, xmm6
// F := (F * N);
// Result := Result + F * PDouble(gSinAddr + 24)^;
mulsd xmm1, xmm2
mulsd xmm7, xmm1 //FSinTab[3]
addsd xmm0, xmm7
// F := (F * N);
// Result := Result - F * PDouble(gSinAddr + 32)^;
mulsd xmm1, xmm2
mulsd xmm8, xmm1 //FSinTab[4]
subsd xmm0, xmm8
// F := (F * N);
// Result := Result + F * PDouble(gSinAddr + 40)^;
mulsd xmm1, xmm2
mulsd xmm9, xmm1 //FSinTab[5]
addsd xmm0, xmm9
// F := (F * N);
// Result := Result - F * PDouble(gSinAddr + 48)^;
mulsd xmm1, xmm2
mulsd xmm10, xmm1 //FSinTab[6]
subsd xmm0, xmm10
// F := (F * N);
// Result := Result + F * PDouble(gSinAddr + 56)^;
mulsd xmm1, xmm2
mulsd xmm11, xmm1 //FSinTab[7]
addsd xmm0, xmm11
//-----------------------------------
// if Minus then
// Result := (Result * QSinSignM[D]) else
// Result := (Result * QSinSignP[D]);
shl rax, 3 //Умножаем на 8
cmp cl, 1
je @Minus
lea rdx, qword ptr [QSinSignP]
mulsd xmm0, qword ptr [rdx + rax]
ret
@Minus:
lea rdx, qword ptr [QSinSignM]
mulsd xmm0, qword ptr [rdx + rax]
end;
Initialization
//Выровненный массив
SetLength(gSinTab, 8);
//Адрес таблицы
gSinAddr := UInt64(@FSinTab[0]);
//Копируем таблицу в выровненный массив
Move(FSinTab[0], gSinTab[0], SizeOf(Double) * 8);
Finalization
SetLength(gSinTab, 0);
Пример работы здесь
Конструктивные предложения и замечания приветствуются.
Комментарии (72)

Rsa97
13.11.2018 23:08Там, где не нужна особая точность, можно использовать формулу Бхаскара:
sinx = 16x(??x)/(5???4x(??x)), x ? [0, ?]
Она даёт максимальную ошибку 0.0016.
Alexeyslav
14.11.2018 10:22+1С такой ошибкой, можно попытаться реализовать функцию таблично. Пара умножений(интерполяция), проверка условия и выбор из таблицы на ~10000 элементов, не?

Rsa97
14.11.2018 12:28Табличный метод быстрее, но есть больше памяти. Вопрос только в том, что именно надо экономить в каждом конкретном случае.

eDmk Автор
14.11.2018 12:46У меня есть таблицы. Они действительно быстрее.
Но вот размер массива для Single при точности угла:
0,1 (~56.25 Кб)
0,01 (~562.5 Кб)
0,001 (~5,49 Мб)
0,0001 (~54,9 Мб)
0,00001 (~549,3 Мб)
0,000001 (~5,36 Гб)
0,0000001 (~53,64 Гб)
maisvendoo
14.11.2018 13:21+1А никто не заставляет рассчитывать каждое значение. Предлагается взять ряд узловых точек, а между ними воспользоваться линейной аппроксимацией

Refridgerator
14.11.2018 14:14+2Для точных табличных вычислений совсем не обязательно использовать такие гигантские объёмы, если использовать тригонометрические тождества. В своей библиотеке я считаю синусы с точностью ?30 знаков используя 4 таблицы по 64 элемента.

Alexeyslav
14.11.2018 14:44+1Вот это уже интересно. Поидее в виду симметричности в памяти можно хранить лишь часть таблицы 0...45 градусов.

Refridgerator
14.11.2018 15:19+1Симметричность — само собой. Алгоритм основан на тождестве
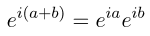
после каждой итерации которого b приближается к нулю. Синус и косинус таким образом считаются одновременно.

eDmk Автор
14.11.2018 15:52-1Неверно. От 0 до 90.

Refridgerator
14.11.2018 16:18+1Нет, верно. При использовании тригонометрических тождеств 45° достаточно.

eDmk Автор
14.11.2018 16:23-1Т.е. по вашему Sin 15° = Sin 75°?
Вот по модулю Sin 105° = Sin 75°, но это переход через 90°.
Симметричность проходит через квадранты, а по октетам требуются доп. вычисления.
Refridgerator
14.11.2018 16:48По-нашему, sin(45°)=cos(45°), а «тригонометрические тождества» и означают дополнительные вычисления.

Alexeyslav
14.11.2018 17:19+2Это означает что sin(15) = cos(90 — 15), ось симметрии проходит через угол в 45 градусов. Тоесть это означает что достаточно хранить в памяти таблицу sin и cos для углов 0...45 чтобы вычислять sin и cos таблично для любого угла с дополнительной проверкой условия и одной арифметической операцией.

eDmk Автор
14.11.2018 17:33Да. Ценное замечание. На выходных переделаю SinCos в единую функцию. Будет и быстрее и, что самое важное, точность будет до 15 знака, т.е. весь Double, т.к. до 45° ряд сходится замечательно вплоть до 17 знаков. Спасибо!

eDmk Автор
14.11.2018 20:15Вообще то неверно. По запросу они равны или если вам так угодно тождественны, а вот по ряду и ответу нет. Симметричность идет до PI / 2.0, а это 90°. Нельзя вычислить sin 75°, зная, что это всего лишь cos 15°. По ряду это более 45°, а значит симметричность нужно брать от квадрантов. Мое предыдущее ликование было преждевременным.
Считаем в радианах же, так вот:
Sin 15° — 0,258819045102520
Cos 15° — 0,965925826289068 < — ряд выше 45°
Sin 75° — 0,965925826289068 < — ряд выше 45°
Cos 75° — 0,258819045102520
Так что симметрия должна быть относительно 90°, т.е. по квадрантам.
Refridgerator
15.11.2018 09:01Если вывести графики синуса и косинуса одновременно, симметрия относительно 45° легко прослеживается:
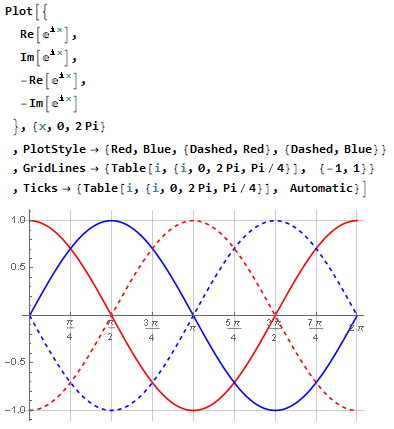
И в вашем примере с 75° и 15° симметрия также легко прослеживается:


Rsa97
15.11.2018 09:15А теперь имея только таблицу значений sin от 0 до ?/4 посчитайте линейными методами sin(?/3).

Refridgerator
15.11.2018 09:57А теперь идите в начало ветки и ищите там фразу «тригонометрические тождества» и формулу с комплексной переменной.

bopoh13
15.11.2018 12:38Синус и косинус таким образом считаются одновременно.
И занимают памяти как одна таблица для sin от 0 до ?/2.
Refridgerator
15.11.2018 12:52Для обеспечения одной и той же точности две таблицы от 0 до pi/4 с синусами и косинусами будут занимать меньше места, чем одна таблица с синусом от 0 до pi/2. Нужно будет только значения из них комплексно перемножить — это два сложения и четыре умножения.

bopoh13
15.11.2018 13:48Алгебраически это интересно. Но в Delphi модуль для работы с комплексными числами имеет
чёрный ящикассемблерные вставки; а в прочих вариантах применяется операция деления.
Refridgerator
15.11.2018 14:00Это интересно не только алгебраически, но и практически — особенно если нужна высокая точность, о чём автор статьи также упоминал:
К сожалению свести ряд «идеально» для Double не получается… достигнутая точность результата равна: 10.e-13

eDmk Автор
15.11.2018 11:13Sin 30° = 1/2, как вашим методом вычислить Sin 60°, который равен Sqrt(3)/2? Они же симметричны относительно 45°?!

Refridgerator
15.11.2018 12:42Точно так же, как и в прошлый раз — поменять действительную и мнимую часть местами:
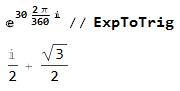
В таблице хранится и синус, и косинус. Если синус и косинус используются для вращения векторов — они обычно считаются от одного и того же угла, поэтому и имеет смысл вычислять их одновременно. И даже если косинус не нужен — на последней стадии вычислений его можно просто не вычислять.
eDmk Автор
15.11.2018 13:14У меня нет таблиц. Ваш метод не подходит.

Refridgerator
15.11.2018 13:24Мой метод работает быстрее и точнее — поэтому ваш метод мне не подходит тоже. И лично я не вижу принципиальной разницы между выделением памяти под таблицы и выделением памяти под это:
скрытый текстFSinTab: array[0..7] of Double =
(1.0 / 6.0, //3!
1.0 / 120.0, //5!
1.0 / 5040.0, //7!
1.0 / 362880.0, //9!
1.0 / 39916800.0, //11!
1.0 / 6227020800.0, //13!
1.0 / 1307674368000.0, //15!
1.0 / 355687428096000.0); //17!
eDmk Автор
15.11.2018 13:49-1Замечательно, просто пройдите мимо.

Refridgerator
15.11.2018 13:52Замечательно, просто пройдите мимо.
Вы же вроде писали «конструктивные предложения и замечания приветствуются»? Не писали бы, прошёл бы мимо.
eDmk Автор
15.11.2018 13:53У вас нет конструктивных предложений. Через ряд Тейлора ваш метод не работает. А одновременное вычисление я напишу позже и выложу в другой статье.

picul
13.11.2018 23:22+2Или я не понял посыла статьи, или Вас ждет небольшое разочарование, ведь для синуса/косинуса и ряда других тригонометрических функций есть соответствующие инструкции, и наличие их 128-битных вариантов гарантируется при наличии самого простого SSE.

eDmk Автор
13.11.2018 23:41-2128 бит — это AVX. Его пока поддерживают не все процессоры. SinCos в SIMD вообще отсутствует. Там только квадратный корень есть.

picul
14.11.2018 00:27+2Нет, 128-битные регистры — это атрибут SSE, а AVX — это уже 256 бит. Но насчет хардварной тригонометрии я действительно не прав — детальный гугл показал, что эти функции принадлежат интеловской проприетарной библиотеке.
Вообще если уж используется SSE, то грех умножать скаляры. Можно ведь сложить в вектора и умножать по 2 double'а за раз. И условных переходов у Вас многовато, наверняка они много времени отъедают. Например, в конце, когда нужно поменять знак в зависимости от модуля угла, можно вместо умножения использовать xor с масками от cmpss.
eDmk Автор
14.11.2018 00:50-1Все верно. Эта библиотека по подписке немало стоит. Так что свой вариант выгоднее.
Сравнение (cmp) занимает ровно 1 такт.
RedApe
14.11.2018 06:58+2А как же ошибки предсказания перехода?

eDmk Автор
14.11.2018 09:57-2Это уже внутренняя кухня интел. Я тут не при чем.

Alexeyslav
14.11.2018 10:26+3А вот это зря. Именно оптимизация такого рода и даёт основной выигрыш в скорости. Толку от быстрого алгоритма, если каждый переход конвеер процессора будет сбрасываться? Иногда бывает быстрее посчитать лишнего чем сделать условный переход. Причем это актуально как для INTEL так и AMD.

impwx
13.11.2018 23:27+15Вы перепутали Хабр и Gist. Без описания того, что вы делаете и почему, простыня кода не становится статьей.

eDmk Автор
13.11.2018 23:48-6Это сделано для ускорения вычислений. Там же все написано. Ряд Тейлора прекрасно описан на Вики (раздел Тригонометрические функции): ru.wikipedia.org/wiki/%D0%A0%D1%8F%D0%B4_%D0%A2%D0%B5%D0%B9%D0%BB%D0%BE%D1%80%D0%B0
Лучше чем там, я не распишу.

akhmelev
14.11.2018 00:23+4Готовый предрасчитанный ряд на несколько тысяч значений + линейные аппроксимации будут сильно быстрее. Это если вам именно скорость важна. И не только для тригонометрии годится. Единственно что в этом случае грозит — вымывание ряда из кеша процессора. Без вымывания — просто полет. Когда-то учил ИНС, так делал для функций активации. Песня.

eDmk Автор
14.11.2018 00:53Да, скорость очень важна. При трансформации, например, 10 тысяч объектов это очень заметно.

akhmelev
14.11.2018 01:04+3Ну тогда попробуйте построить в памяти свои «таблицы брадиса». Индекс массива — агрумент (привести к целочисленному дело техники надеюсь), а значения — предрассчитанные sin или cos. Т.к. sin и cos неплохо аппроксимируются даже линейно в итоге должно быть сильно быстрее Тейлора и вообще всего возможного. Можно конечно улучшить точность квадратичной или кубической аппроксимациями, но тогда проигрыш в скорости будет сразу заметен, т.к. простая пропорция это очень быстро, не обогнать.

fishca
14.11.2018 11:27Кстати этот прием всегда описывался при программировании 3D графики, еще в стародавние времена.

Refridgerator
15.11.2018 09:44В кубической аппроксимациями тоже есть место для оптимизации. Можно вообще ничего не считать, а просто хранить уже посчитанные 4 коэффициента, а сам кубический полином считать схемой Горнера — будет 3 сложения и 3 умножения.
Можно вообще использовать аппроксимацию рациональным полиномом, а коэффициенты для него считать методом наименьших квадратов.
akhmelev
16.11.2018 21:07Да, конечно, все так. Автор просто скорость хотел, вот я ему самое быстрое и посоветовал, две операции или шесть — разница в три раза. Опять-таки кеширование таблицы даже важнее числа операций, если она большая и много коэффициентов, то вылезет из кеша, а это сразу аппаратные уже тормоза. И серьезные, на порядок минимум.
В разрезе скорости МНК не вариант я думаю, но математически — да, можно получить любую нужную точность. Впрочем как и Тейлором.
eDmk Автор
16.11.2018 21:19У меня готовая таблица с точность 0.001. Скорость выборок более 500 млн в сек.
Это более чем в 10 раз быстрее моего метода и в 12-13 раз быстрее CPU или библиотечного. Но интерполяция значений не требуется из за достатка точности.

Refridgerator
16.11.2018 21:34В разрезе скорости МНК не вариант
через МНК коэффициенты считается заранее и один раз, их не нужно постоянно пересчитывать. Таким образом часто неэлементарные функции считают — вот тут, например.

Refridgerator
14.11.2018 14:00А ещё рассчитанные значения можно хранить вместе с производными и использовать кубическую, а не линейную интерполяцию.

xgbaggins
14.11.2018 05:36-5А delphi разве всё еще где-то актуален??
И вообще всё это ковбойство с ассемблером в наше время ну вот совершенно вот ни к чему, если только ты не компилятор пишешь. В твоём Core-i7 6950X Extreme есть например AVX2 с аппаратным векторизованным sin/cos, который хороший векторизующий компилятор скорее всего сам и врубит, или до которого ты в крайнем случае с минимальным геморроем через какую-нибудь серьезную матбиблиотеку достучишься, например Eigen для плюсов. Скорее всего сразу в разы быстрее c ним станем. Еще на порядок быстрее будет с GPU.
LAutour
14.11.2018 06:15Зачем учиться думать самому — компилятор всегда думает за вас.

xgbaggins
14.11.2018 06:30Вы лучше учитесь думать абстракциями, намного плодотворнее время потратите, может и зарплата вырастет заодно. Компилятор — всего лишь инструмент, абстракция над машинными инструкциями. Да, бывают моменты когда ее нужно приподнять, но будет ли это целесообразно и лучшей тратой вашего времени?
Конкретно в вашем описанном случае я думаю нет — компилятор/матбиблиотека умеют в AVX2, а ваш код нет, шах и мат. Что целесообразнее — курить сейчас Intel Software Developer's Manuals и молиться чтобы ассемблер в delphi поддерживал AVX2, или же просто подключить подходящую библиотеку? А если у пользователя AMD? А если лет через 10 никому н*х этот x86 уже не нужен будет и весь мир на ARM будет сидеть, кто оплатит переписывание вашего куска кода?
eDmk Автор
14.11.2018 10:03ARM умеет [+, -, /, *]. Мой код спокойно переносится на ARM. Не переживайте.

eDmk Автор
15.11.2018 10:20Представляете читаю Intel Software Developer's Manuals на досуге.
AVX в Delphi будет. Мне пока достаточно опкодов из Лазаруса, который поддерживает AVX, AVX2.

maisvendoo
14.11.2018 07:17И вообще всё это ковбойство с ассемблером в наше время ну вот совершенно вот ни к чему,
Потому, что одно из главных качеств в наше время кода — переносимость. А ассемблер не переносим по определению. Тем более в виде вставок в высокоуровневый код
Только вот у меня вопрос к автору — зачем вычислять отдельно cos(x) если
cos(x) = sin(П/2 — x)
Хватит одного синуса
eDmk Автор
14.11.2018 10:01Так у меня косинус выражен через синус. Там есть небольшая почти незаметная вставочка:
if Minus then AMod := Abs(A) — PI90 else AMod := Abs(A) + PI90; Это вся разница между sin и cos.

LAutour
14.11.2018 11:17По переносимости: в самых кроссплатформенных С\С++ программах обычно для обеспечения переносимости используют кучу различных кусков кода с условной компиляцией под разные компиляторы\платформы.

eDmk Автор
14.11.2018 10:10+1В SIMD (на уровне инструкций) есть только SQRT. Delphi прекрасная среда, не уступающая по своим возможностям VS.

xgbaggins
14.11.2018 22:34-2Лет 15-20 назад, да, прикольная была система, но поезд давно ушел. Кому она сейчас нужна, кроме тех у кого горы legacy паскаля в проекте? Геймдев чуть менее чем на 100% сидит на плюсах. UI/RAD почти всем сейчас нужен через веб, там рулит javascript в т.ч. уже и на бэкэнде (nodejs), время настольных приложений постепенно уходит
>Delphi прекрасная среда, не уступающая по своим возможностям VS
Джуновский такой комментарий как будто вы всю жизнь ни на чем кроме делфи не сидели. Как по мне так оба просто инструменты, одни из многих, для достижения цели проекта, и не факт что лучшие
picul
14.11.2018 22:56Во-первых, статья не совсем про Delphi, она про асмовский код, который запросто можно использовать и в C++. Во-вторых, Delphi — хоть и не бурно развивающаяся, но очень даже неплохая система, с помощью которой делать UI сильно приятнее, чем с помощью, прости Господи, жабаскрипта. Ну и в-третьих, а чисто для развлечения программировать запрещено, все должно быть обусловлено положением на рынке?
Как по мне так оба просто инструменты, одни из многих, для достижения цели проекта, и не факт что лучшие
PM-овский такой комментарий.

eDmk Автор
15.11.2018 01:07Поезд все там же, просто с первого пути перевели на 7-й, но не в тупик.
Продукт развивается и вполне успешно.

mobi
14.11.2018 20:35За основу для вычислений взял разложение по ряду Тейлора.
Почему? Почему не CORDIC, или если так уж хочется ряды, то почему не Чебышев?
eDmk Автор
15.11.2018 01:04Кордик запатентован вроде, а до Чебышева пока руки не дошли.
Просто Тейлор самый шустрый при приемлемой точности. Остальные точнее, но медленнее.
В конце-концов я никому не навязываю свой вариант. Это просто вариант.


f1inx
по сравнению с fsin/fcos/fsincos какой выигрыш в производительности?
latency/Reciprocal throughput какой получился?
Параллельно за 1 проход сразу несколько аргументов пробовали обрабатывать (так обычно быстрее)?
eDmk Автор
Сделал тест в одном потоке — 1 млрд вызовов с присваиванием переменной:
CPU.(FPU) ~ 32.7 (максимум 42.8) млн/сек.
Math.Sin ~ 58 (максимум 70.1) млн/сек.
Мой SIMD.Sinf ~ 147.0 (161.2) млн/сек.
Результат плавает из-за загрузки системы. Корректно измерить не получается.
Без скобок результат параллельной работы Chrome. В скобках максимум при «простое» системы. Windows 10 (x64).