Работа Александра Смита по гипотезе Голдфелда раскрыла фундаментальные свойства эллиптических кривых
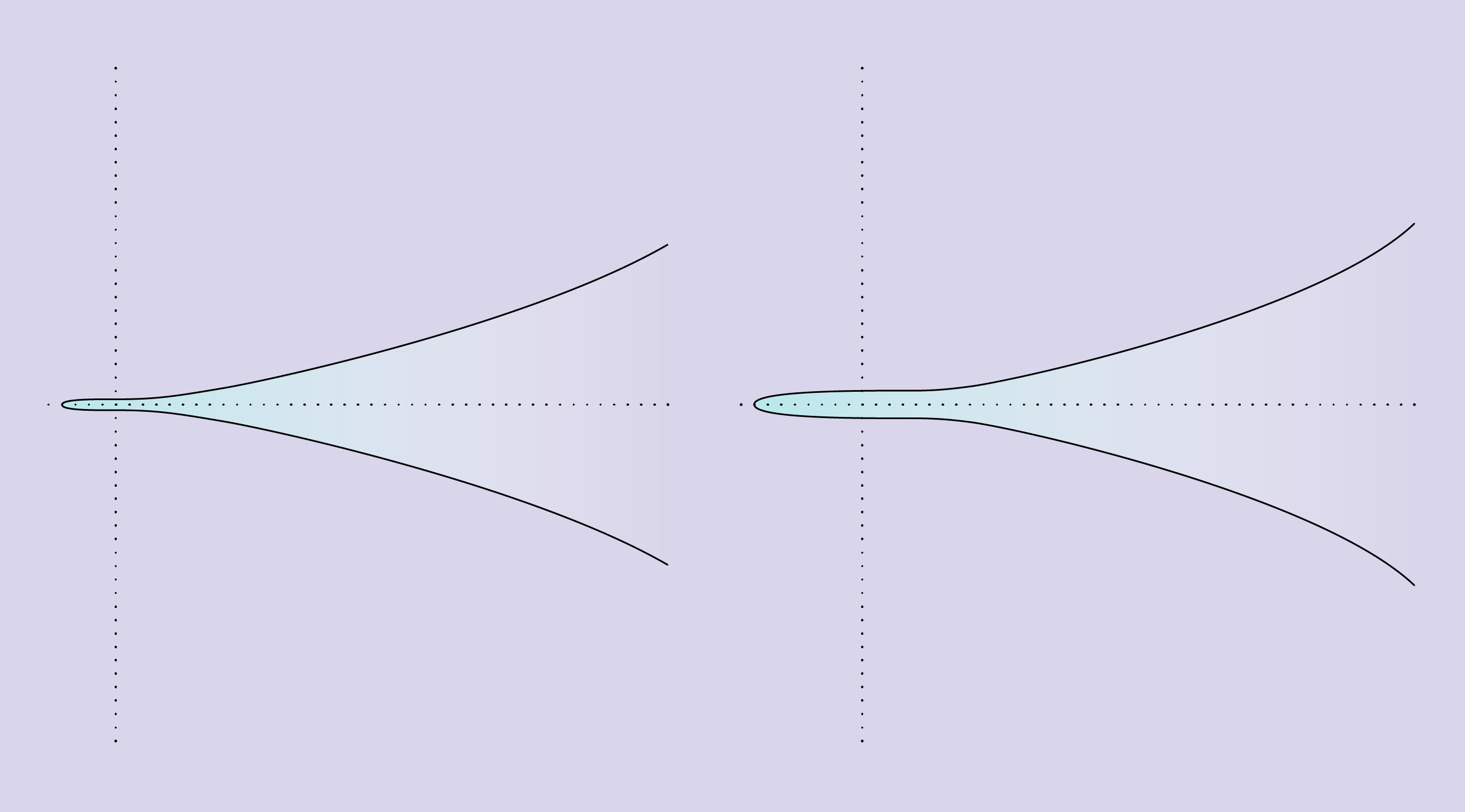
Две эллиптические кривые демонстрируют странности концепции ранга. Кривая слева описывается уравнением y2 = x3 + 1, проходит только через пять рациональных точек и имеет ранг 0. Кривая справа описывается уравнением y2 = x3 + 8, проходит через бесконечное число рациональных точек, и имеет ранг 1.
Вариантов эллиптических кривых может быть много, но их реальных разновидностей всего две. Таков итог нового доказательства, полученного аспирантом из Гарвардского университета.
Эллиптические кривые кажутся чем-то экзотическим, однако это непримечательные геометрические объекты, не сложнее прямых, парабол или эллипсов. В своей работе, опубликованной в онлайне в прошлом году, Алексадр Смит доказал гипотезу сорокалетней давности, касающуюся фундаментальной особенности эллиптических кривых, ранга. Смит доказал, что из определённого семейства кривых, имеющих одну характеристику, половина имеют ранг, равный 0, а половина – 1.
Этот результат устанавливает опорную характеристику объектов, занимавших математиков много веков, чья важность особенно возросла в последние десятилетия.
«Мы думали об этом более 1000 лет, и теперь у нас появилось вероятностное понимание эллиптических кривых. Это чрезвычайно важно», — сказал Шоу-У Чжан, математик из Принстонского университета, дававший Смиту рекомендации по его работе, когда тот был ещё студентом в Принстоне.
Эллиптические кривые – это уравнения с переменными, возведёнными в третью степень, например, y2 = x3 + 1. Они фигурировали во многих значимых математических доказательствах в последние десятилетия, включая важнейшее доказательство Великой теоремы Ферма от 1994 года. Часть их значимости состоит в том, что они принадлежат к самому сложному типу полиномиальных уравнений, о котором у математиков есть какие-то системные представления.
«Эллиптические кривые – это интересный случай», — сказал Дориан Голдфелд, математик из Колумбийского университета, предложивший в 1979 гипотезу, получившую его имя.
Гипотеза Голдфелда делает предсказания по поводу ранга эллиптических кривых. Как мы уже описывали в недавней статье "Какие свидетельства могут убедить математиков, если строгого доказательства нет?", ранг – это мера сложности набора рациональных решений кривой (решений, которые можно представить в виде дробей). И хотя не существует доказанного ограничения величины ранга кривой – пока что самым высоким рангом из обнаруженных считается величина 28 – гипотеза Голдфелда предсказывает, что в среднем у половины эллиптических кривых ранг равен 0, а у другой половины – 1.
Вам может показаться непонятным, как могут существовать эллиптические кривые рангом более 1, если у половины эллиптических кривых ранг равен 0, а у другой половины – 1. Если у вас есть коробка шариков для пинг-понга, и если вы знаете, что ровно половина из них чёрные, а половина – белые, то красных там быть не может.
Ещё сильнее запутывает тот факт, что эллиптических кривых с рангом 2 или выше существует не просто несколько, а бесконечное количество. Кажущийся абсурдным результат является следствием хитрой статистики, работающей с бесконечностями. Даже несмотря на то, что кривых рангом 2 и выше есть очень много, кривых с рангами 0 и 1 настолько больше, что кривые с рангами 2 и выше статистически не имеют значения. Если сложить все кривые в коробку и вынимать их оттуда случайным образом, то шансы вытащить кривую с рангом более 1 официально приравниваются к нулю.
Что означает, что ранг кривой равен 0? У таких кривых есть конечное количество рациональных точек – причём не более 16, как доказал ещё Барри Мазур в 1970-х.

Дориан Голдфелд
Есть причины полагать, что у очень большого количества эллиптических кривых ранг будет равен 0. Если представить, как кривая бежит по плоскости, будет видно, что большая часть точек, через которых она проходит, не будут рациональными. Эти точки нельзя выразить в виде дробей, пусть даже сколь угодно сложных. Шансы на то, что случайная кривая пересечёт множество рациональных точек – бесконечное множество – малы.
«Я отношусь к этому так: если взять случайную эллиптическую кривую, то у неё будут причины иметь ранг 0. Она не хочет иметь рациональных точек», — сказал Смит.
Распространённость кривых ранга 1 объясняется сходным образом. У кривых ранга 1 есть бесконечно много рациональных точек, однако все они очень аккуратно выстраиваются, так, что соединять их друг с другом можно в рамках довольно простого процесса.
У кривых рангом 2 и выше наборы рациональных точек устроены сложнее. В них содержатся несколько бесконечных подмножеств рациональных точек, не связанных друг с другом.
«Каковы шансы на появление двух независимых точек? – сказал Голдфелд. – Весьма низки. Моя гипотеза говорит, что такое должно происходить редко».
Когда Голдфелд впервые выдвинул свою гипотезу, большинство математиков посчитали её неверной. Они указывали на результаты вычислительных экспериментов, из которых следовало, что кривые с рангом 2 или выше возникают гораздо чаще, чем в 0% случаев.
Голдфелд ответил, что они просто берут слишком маленький диапазон. Он указал, что если изучать только первые 10 целых чисел, то можно получить чрезвычайно неточную оценку того, что 40% чисел являются простыми. Точно так же эти вычислительные эксперименты экстраполировали от небольших подмножеств эллиптических кривых к бесконечно большим семействам кривых.
«Я сказал – посмотрите на простые числа! Таков был мой ответ. Нужно забираться гораздо выше, потому что в начале может появляться много забавного», — сказал Голдфелд.
Гипотеза Голдфелда относится не ко всем эллиптическим кривым. Она описывает особое семейство эллиптических кривых, квадратичные изгибы [quadratic twists]. Пример: эллиптическая кривая cy2 = x3 ? x, где c – некая константа. Изменяя значение c, вы изгибаете эллиптическую кривую. Гипотеза Голдфелда относится ко всему бесконечному разнообразию кривых, которое можно получить, изменяя значение c.
Александр Смит показал, что Голдфелд был прав. В новой работе он доказывает, что 100% эллиптических кривых (особого рода) имеет ранг 0 или 1. Он т акже доказал, что эти кривые поровну разделяются между двумя рангами, хотя тут есть и подвох. Его доказательство разделения 50 на 50 основывается на справедливости гипотезы Бёрча — Свиннертон-Дайера (БСД). Гипотеза БСД – одна из известнейших открытых проблем математики. Математики пока и близко не подошли к её доказательству, но в целом считают её верной.
Даже с такой оговоркой, результат Смита считается весомым. Математики говорят, что он показывает способ полностью доказать гипотезу Голдфелда, не возясь с обескураживающей гипотезой БСД. Этот способ даёт новое понимание природы эллиптических кривых.
«Работа Алекса Смита чрезвычайно интересна, и я думаю, её ещё предстоит как следует изучить и воздать по заслугам», — сказала Мелани Вуд, математик из Висконсинского университета. «То, что это можно доказать – это очень важно и революционно».
Комментарии (35)

rjhdby
26.11.2018 16:54Меня обуревают противоречивые чувства — статья крайне увлекательна, но совершенно непонятна.

Deerenaros
27.11.2018 13:09Это она ещё довольно простым языком написана. Буквально на пальцах. Математики во всю используют собственный «японский» с мерами, мощностями, ординалы, кардиналы, многообразия, а когда появились компьютеры придумали машину Тьюринга и понеслось: вычислимость (проблема останова), односторонние (?) функции (криптосистемы), хеш-суммы, дискретизация и сглаживания, энтропия (!) и прочая дичь. Но это ещё цветочки по сравнению с диким матоаном, фуаном и совершенной лабудой в квантовой механике: мнимые числа покажутся буквально реальными и осязаемыми.

aleksandros
27.11.2018 13:25+1А меня слегка расстраивает то, что Mathematica и Mapple рисуют только верхнюю, положительную часть графика и я не знаю как построить всё)

razielvamp
27.11.2018 07:39А что значит
большая часть точек, через которых она проходит, не будут рациональными. Эти точки нельзя выразить в виде дробей, пусть даже сколь угодно сложных
?
Я могу понять, что дробь X/0 действительно неоднозначна, но какие еще числа не могут быть выражены в виде дроби? Или, когда говорится точка, подразумеваются не числа координат?
Druu
27.11.2018 08:09Я могу понять, что дробь X/0 действительно неоднозначна, но какие еще числа не могут быть выражены в виде дроби?
Корень из двух, например, не может.
https://ru.wikipedia.org/wiki/%D0%9A%D0%B2%D0%B0%D0%B4%D1%80%D0%B0%D1%82%D0%BD%D1%8B%D0%B9_%D0%BA%D0%BE%D1%80%D0%B5%D0%BD%D1%8C_%D0%B8%D0%B7_2#%D0%94%D0%BE%D0%BA%D0%B0%D0%B7%D0%B0%D1%82%D0%B5%D0%BB%D1%8C%D1%81%D1%82%D0%B2%D0%BE_%D0%B8%D1%80%D1%80%D0%B0%D1%86%D0%B8%D0%BE%D0%BD%D0%B0%D0%BB%D1%8C%D0%BD%D0%BE%D1%81%D1%82%D0%B8

Deosis
27.11.2018 08:54+1Если говорят, что число нельзя представить в виде дроби, то обычно подразумевают, что у такой дроби должен быть целый числитель и натуральный знаменатель.

Aquahawk
27.11.2018 12:04Смотрите, числа 3/0 не существует. Т.е. его просто нет. А число корень из 2 существует, просто оно не выразимо в виде рациональной дроби. Но число существует, понятно и определено. Мы просто не можем его записать такой формой записи.

untilx
27.11.2018 14:19Пи, золотое сечение, корни из простых чисел, экспонента — любые иррациональные числа (по определению).

lega
27.11.2018 11:16Очень интересно, но как это применить к реальной жизни?

kirtsar
27.11.2018 11:45Изначально многие объекты в математике возникают просто потому, что математикам интересно их изучать. Конкретно эллиптические кривые используются повсеместно в криптографии. Чтобы криптографическая схема на эллиптической кривой была достаточно стойкая, требуется, чтобы «группа точек» на этой кривой была «достаточно хорошей». Поэтому всё, что касается группы точек, представляет некоторый интерес со стороны практики: даже если эти методы и не могут быть применены напрямую для изучения необходимых в криптографии кривых (а они там, вообще говоря, рассматриваются над конечными объектами — полями Галуа, а не над всеми рациональными числами), то всё равно могут навести на новые идеи.

jazator
27.11.2018 16:41— Ты, наверное, думал, что математика — это то, что вам рассказывают в школе, — продолжил Евгений Евгеньевич. Он покачал головой. — Нет, вот, — он указал пальцем на формулы в книге, — истинная математика. Если ты хочешь по-настоящему понять квантовую физику, то начать тебе следует с этого. Гелл- Ман предсказал существование кварков с помощью красивой математической теории.
Эдуард Френкель, «Любовь и математика».

trapwalker
27.11.2018 14:25+1У кого есть про-аккаунт на вольфраме? Игрался игрался и нашел такую занятную штуку:
plot3d z*y^2 = x^3 ? x+z, x=-2..2, y=-2..2, z=-2..2
Теперь сгораю от любопытсива как в ней дырки устроены. Не понятно с ракурса по умолчанию. А повернуть на бесплатном не дает.
unclegluk
27.11.2018 16:27
trapwalker
27.11.2018 17:41Круто! Спасибо.
Прекрасно же!

vesper-bot
27.11.2018 18:03Как я понимаю, плоскость z=0 для этой структуры особенная, так как при z=0 решениями являются любой Y и x=0, 0 и 1 (т.е. две прямые x=0,z=0 и x=1,z=0), посему и не сглаживается нормально.

unclegluk
28.11.2018 01:58Я не настоящий сварщик, но мне кажется, что оно лезет из двумерного уравнения, где около нуля бывает пустое место решений. А тут просто появилась третья координата.

aleksandros
27.11.2018 20:53Кстати, почему-то графики в Mathematica и Mapple при прочих равных весьма отличаются.
Заголовок спойлера


unclegluk
28.11.2018 02:04Я использовал Графер из Макоси. Просто перенес y^2 в правую часть. У вас немного другие уравнения, надо будет поглазеть на графики.

aleksandros
28.11.2018 08:50Ну, уравнение то же, ведь z*y^2 = x^3 ? x+z преобразуется в z=(x^3-x)/(y^2-1).

unclegluk
28.11.2018 21:40А зачем вы убрали +z и добавили -1? В таком виде картинка меняется радикально. Кстати, уравнение без переноса y^2 выглядит без разрыва по середине.

aleksandros
28.11.2018 21:47Смотрите, исходное выражение z*y^2=x^3?x+z
1) Переносим z влево: z*y^2-z=x^3-x
2) Выносим z за скобки: z(y^2-1)=x^3-x
3) Делим левую и правую часть на выражение в скобках: z=(x^3-x)/(y^2-1)
Druu
29.11.2018 03:503) Делим левую и правую часть на выражение в скобках: z=(x^3-x)/(y^2-1)
На ноль делить нельзя

aleksandros
29.11.2018 08:40Мы делим не на 0, а на переменную, вы чего, это же 5-й класс. Например, x*y=1 равносильно y=1/x или x=1/y.

Druu
29.11.2018 10:10Мы делим не на 0, а на переменную
Которая может быть равна нулю. То есть ваше выражение эквивалентно исходному только при условии y^2-1 != 0.
Например, x*y=1 равносильно y=1/x или x=1/y.
Угу, а 2*2=5 потом :)

vesper-bot
29.11.2018 09:19Если знаменатель равен нулю, достраиваем по остатку уравнения «числитель=0», заодно проверяем исходное в этих точках. Готово.

ITNA
28.11.2018 11:48-1Объясните пожалуйста, как строятся графики на картинке?
Не понятно почему y^2 могут иметь отрицательные значения, и почему х не могут быть меньше показанных на графике.

StrausMG
28.11.2018 11:48Можно в качестве примечания переводчика пару слов о том, зачем это надо? И предпочтительно услышать конечное применение для людей, а не для другой абстрактной задачи.


vesper-bot
Вот интересно, «100% кривых особого рода» — это «все» или все-таки «почти все», т.е. множество неподходящих кривых имеет нулевую меру?
vmspike
Тут, мне кажется, не совсем обычные проценты, когда речь идёт о бесконечностях. Вот, например, сколько процентов занимают рациональные числа от вещественных? Или удобнее будет спросить какой процент от комплексных занимают вещественные? Вспомнив поле комплексных чисел и линию вещественных на нём, очевидно, что 0%, тем не менее чисто вещественные числа всё-таки встречаются в комплексных.
vesper-bot
Ну я примерно о том же. Мера множества вещественных чисел на комплексной плоскости, вообще говоря, ноль, то же про меру множества рациональных чисел на числовой прямой. (Лебега, что ли, мера — «обычную» меру оба множества не имеют)
Druu
с-но вероятность — это и есть мера. По-этому «100%» — это по определению «все за исключением меры 0», т.к. если из множества меры 1 вычесть множество меры 0, то получится множество меры 1.
Deosis
С бесконечностями все совсем плохо. Ведь можно показать, что комплексных чисел столько же, сколько вещественных.