волна, колебания, затухающие колебания, волна может быть описана с точки зрения физики, волна может быть описана с точки зрения математики.
Скачать и протестировать программу
Поскольку моделируем мы на компьютере, то наша волна описывается при помощи последовательности (ряда Фурье) из байт (чисел от -128 до 127 и ноля), тоесть массивом байт.
Уравнение колебательных движений лучше всего описывает функция SIN.
Согласитесь было бы слишком просто, если бы мы просто прогнали по массиву функцию SIN.
Поэтому руководствуясь статьями об описании устройства синтезатора Yamaha, я написал следующий алгоритм:
1. При помощи функции SIN создается основная или моделирующая волна, вот формула которая может пригодиться другим разработчика:
for(int k = 0; k < SoundLabVisual.player.data.length;k++){
double sinusoid = amplitude1 * Math.sin(2 * (3.14/1 ) * k * frequency1 + faza);
}
Где:
amplitude1 — амплитуда
frequency1 — частота колебаний
faza — начальная фаза колебаний
2. При помощи второй функци SIN, создается основная волна, амплитудой в которой выступают значения первой волны:
//cдвиг по оси
double a1 = 0.1f;
//cдвиг по оси
double c1 = 0.1f;
//cдвиг по оси
double d1 = 0.1f;
sinusoid = a1 + (sinusoid * Math.sin( (c1 * (double)k) * frequency2Double + d1 ));
Скриншот программы
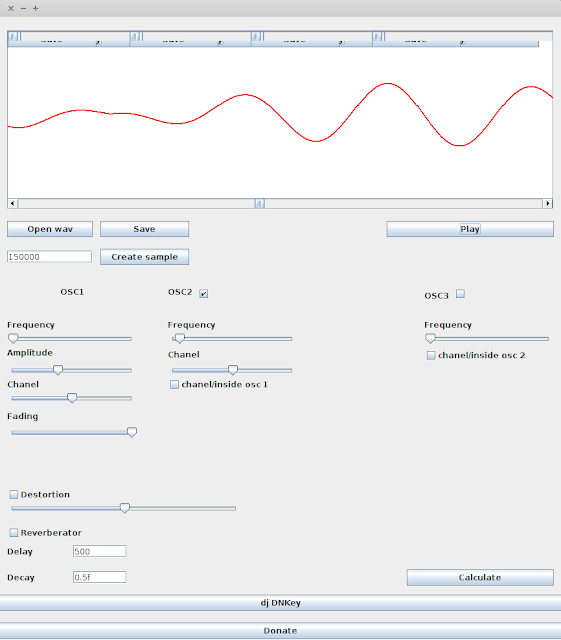
Тестовые звуки я загрузил в программу lmms.

Послушать mp3
Будет реализован другой алгоритм, который будет работать по каналам, если получится напишу о нем во второй статье.
Update:
По замечаниям комментаторов алгоритмы теперь можно перемножать сами на себя и между собой.
if(jCheckBox8.isSelected()){
sinusoid = (a1 + (sinusoid * Math.sin( (c1 * (double)k) * frequency2Double + d1 ))) * (a1 + (sinusoid * Math.sin( (c1 * (double)k) * frequency2Double + d1 )));
}else{
sinusoid = a1 + (sinusoid * Math.sin( (c1 * (double)k) * frequency2Double + d1 ));
}Комментарии (22)

vilgeforce
29.11.2018 13:47+3«Уравнение колебательных движений лучше всего описывает функция SIN.» — насколько хуже колебания описывает функция COS? Чем хуже?

VaalKIA
29.11.2018 14:00+1Это вступление к CSound? На первой картинке, какой-то подозрительный излом на графике, сразу за первой волной, сдаётся мне, вашей проге нельзя доверять.

Padaboo Автор
29.11.2018 14:33Там есть часть кода которая поправляет разрывы и прочие неровности волн, для того, что бы звучание не портилось.

Doberman341
29.11.2018 14:46Модуляция звука, суть, умножение колебательных уравнений. Дает в спектре разностную и суммарную частоты. А у Вас описана суперпозиция волн, то есть — сложение. В спектре будет просто две волны. Зачем в формуле волны делить Пи на единицу?
Ну и непонятно, что же вы хотели сказать данной статьей? Складывается ощущение, что она не доделана…
Padaboo Автор
29.11.2018 14:47Отличная идея, попробую: что умножать сами уравнения или их результаты?
Мой второй вариант волна кторая будет колебаться в канале первой.
Doberman341
29.11.2018 14:55Формулы колебания умножать:
A1*SIN(2*Pi*F1+Ph1) * A2*SIN(2*Pi*F2+Ph2)
Вот это и будет модуляцией.
В спектре дополнительно появятся колебания вида:
A3*SIN(2*Pi*(F1+F2)+Ph1) и A3*SIN(2*Pi*(F1-F2)+Ph1)
А у Вас — наложение волн, это не совсем то…
Padaboo Автор
29.11.2018 14:57Хорошо попробую несколько вриантов:
1) умножить первое уравнение само на себя.
2) первое уравнение на второе
3) первое на первое и второе на второе

Padaboo Автор
29.11.2018 14:58Волный друг на друга не накладываются, просто по первой волне строится вторая.

Padaboo Автор
29.11.2018 16:17После обновления программы нашел звук похожий на колокол спасибо Doberman341


maslyaev
Извините за граммар-нацизм
Padaboo Автор
Поправил
musicriffstudio
"Поскольку"
Извините за граммар-нацизм.
maslyaev
Сдаюсь.
berez
Это не граммар-нацизм, а пунктуационный докоп.