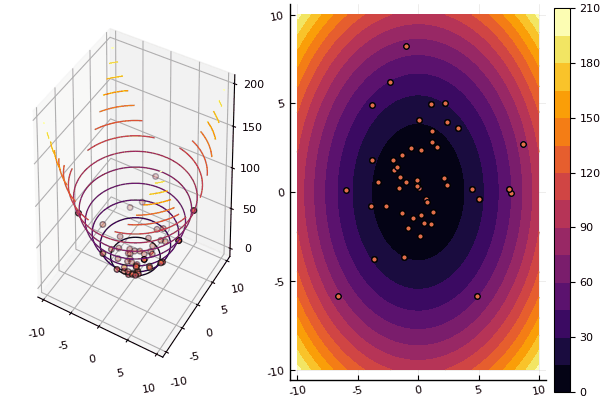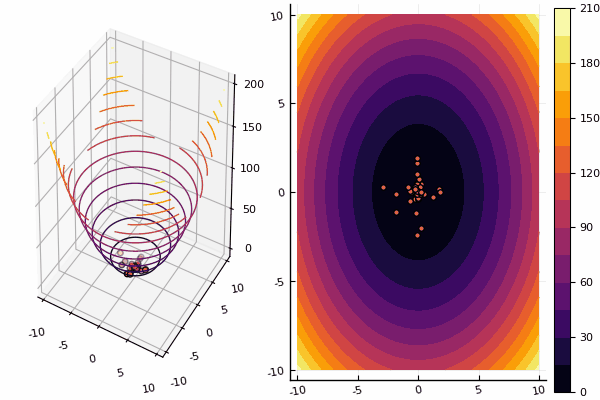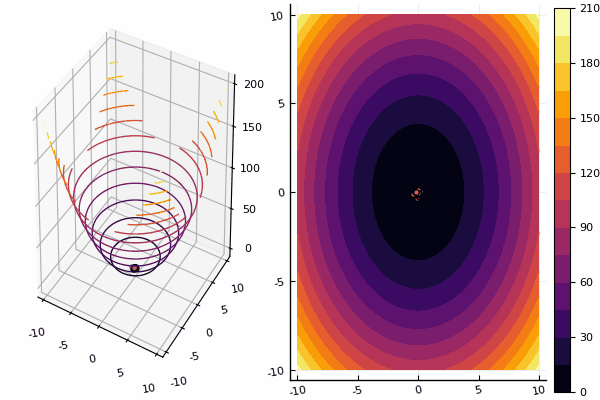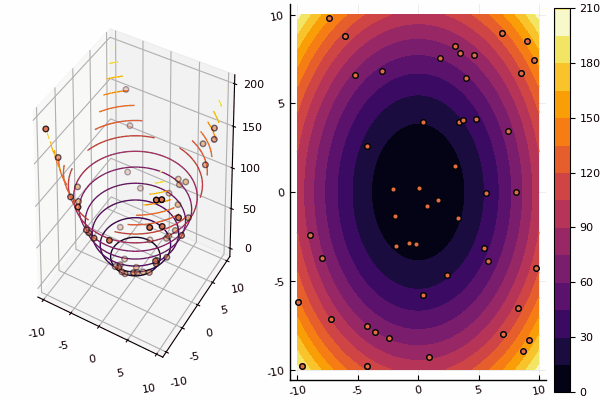
Продолжаем изучение методов многомерной оптимизации, и следующий на очереди — метод роя частиц осуществляющий поиск глобального минимума.

Теория

• Википедия
• Различные методы роя частиц и их топологии
• Рой частиц на Python и C#
• Метод оптимизации стаей котиков

Алгоритм довольно прост:

Положение каждой частицы в определенный момент высчитывается по формуле:

Где $$ — координата лучшего решения конкретной частицы, $$ — координата лучшего решения для всех частиц за эту эпоху, $$ и $$ — весовые коэффициенты (подбираются под конкретную модель), $$ — коэффициент инерции, его можно сделать зависимым от номера эпохи, тогда скорости частиц будут меняться плавно.

Тестовые функции

Так как на работу метода очень приятно смотреть, наберем тестовых функций побольше:

parabol(x) = sum(u->u*u, x) 
# f(0,0) = 0, x_i ? [-10,10]

shvefel(x) = sum(u-> -u*sin(sqrt(abs(u))), x) 
# f(420.9687,420.9687) = -819?, x_i ? [-500,500]

rastrigin(x) = 10*length(x) + sum(u->u*u-10*cos(2*pi*u), x) 
# f(0,0) = 0, x_i ? [-5,5]

ekly(x) = -20exp(-0.2sqrt(0.5(x[1]*x[1]+x[2]*x[2]))) - exp(0.5(cospi(2x[1])+cospi(2x[2]))) + 20 + ?
# f(0,0) = 0, x_i ? [-5,5]

rosenbrok(x) = 100(x[2]-x[1]*x[1])^2 + (x[1]-1)^2 
# f(0,0) = 0, x_i ? [-5,5]

bill(x) = (1.5-x[1]+x[1]*x[2])^2 + (2.25-x[1]+x[1]*x[2]*x[2])^2 + (2.625-x[1]+x[1]*x[2]^3)^2 
# f(3,0.5) = 0, x_i ? [-5,5]

boot(x) = (x[1]+2x[2]-7)^2 + (2x[1]+x[2]-5)^2 
# f(1,3) = 0, x_i ? [-10,10]

bukin6(x) = 100sqrt(abs(x[2]-0.01x[1]*x[1])) + 0.01abs(x[1]+10) 
# f(-10,1) = 0, x_i ? [-15,-5; -3,3]

levy13(x) = sinpi(3x[1])^2 + (1+sinpi(3x[2])^2)*(x[1]-1)^2 + (1+sinpi(2x[2])^2)*(x[2]-1)^2 
# f(1,1) = 0, x_i ? [-10,10]

himmelblau(x) = (x[1]^2+x[2]-11)^2 + (x[1]+x[2]^2-7)^2 
# f(3,2)... = 0, x_i ? [-5,5]

camel3humped(x) = 2x[1]^2 - 1.05x[1]^4 + x[1]^6 /6 + x[1]*x[2] + x[2]^2 
# f(0,0) = 0, x_i ? [-5,5]

izom(x) = -cos(x[1])*cos(x[2])*exp(-( (x[1]-pi)^2 + (x[2]-pi)^2 )) 
# f(?,?) = -1, x_i ? [-100,100]

holdertable(x) = -abs(sin(x[1])*cos(x[2])exp(abs( 1-sqrt(x[1]^2+x[2]^2)/pi ))) 
# f(±8.05502,±9.66459) = -19.2085, x_i ? [-10,10]

shaffer4(x) = 0.5 + (cos(sin(abs(x[1]^2-x[2]^2)))^2-0.5) / (1+0.001(x[1]^2+x[2]^2))^2 
# f(0,1.25313) = 0.292579, x_i ? [-100,100]

И, собственно, сам МРЧ:

function mdpso(;
       nparts = 50,
       ndimes = 2,
       ages = 50, # количество эпох
       lover = [-10 -10],
       upper = [10 10],
       C1 = [1.9 1.9], # весовые коэф-ты
       C2 = [1.8 1.8],
       Ac = [0.1 0.1],
       )

    minind = 0
    V = zeros(nparts,ndimes) # матрица нулей n на n
    X = zeros(nparts,ndimes)
    funmin = -Inf
    Fmin = Inf
    Fbest = fill(Fmin, nparts)
    funx = zeros(nparts)
    xmem = zeros(nparts,ndimes)
    xbest = zeros(ndimes) # лучшая координата

    # частицы разбрасываются по исследуемой области
    for i in 1:nparts, j in 1:ndimes
        X[i,j] = randomer(lover[j], upper[j])
    end

    for i in 1:ages

        for j in 1:nparts

            funx[j] = fun(X[j,:])
            if funx[j] < Fbest[j]
                Fbest[j] = funx[j]
                xmem[j,:] = X[j,:]
            end
        end
         # отрисовывает частицы на каждой эпохе
        ploter(lover, upper, X, funx, i);

        funmin = minimum(funx)
        minind = argmin(funx)

        if funmin < Fmin
            Fmin = funmin
            xbest[:] = X[minind,:]
        end

        for j in 1:nparts, k in 1:ndimes
            R1 = rand()
            R2 = rand()
            V[j,k] = Ac[k]*V[j,k] + C1[k]*R1*(xmem[j,k] - X[j,k]) + 
                C2[k]*R2*(xbest[k] - X[j,k])

            X[j,k] += V[j,k]
        end
        println("Age № $i\n xbest:\n $(xbest[1]) $(xbest[2])")
        println("Fmin: $Fmin\n")
    end

    f = open("$fun.txt","w") # выводим параметры модели в файл
    write(f,"C1 = $C1, C2 = $C2, Ac = $Ac, lower = $lover, upper = $upper, ages = $ages, parts = $nparts")
    close(f)
end

С рисовалками хоть и дольше выполняется расчет, но зато красивей:

using Plots
pyplot()

function ploter(l, u, xy, z, n_age )
    contour(Xs, Ys, Zs, fill = true);
    # легенду не показывать (для каждой блин частицы)
    # задать границы рисунка, чтоб не дергалось кода частица убежала
    scatter!(xy[:,1], xy[:,2], legend = false, xaxis=( (l[1], u[1])), yaxis=( (l[2], u[2])) );
    #savefig("$fun $n_age.png") # создаёт кадры эпох в папке с проектом
end

fun = bill

low = [-4 -4]
up = [4 4]
    Xs = range(low[1], stop = up[1], length = 80)
    Ys = range(low[2], stop = up[2], length = 80)
    Zs = [ fun([x y]) for y in Ys, x in Xs ]

    surface(Xs, Ys, Zs)
    xaxis!( (low[1], up[1]), low[1]:(up[1]-low[1])/5:up[1] )
    yaxis!( (low[2], up[2]), low[2]:(up[2]-low[2])/5:up[2] )

mdpso(C1 = [1.2 1.2], C2 = [1.1 1.1], Ac = [0.08 0.08], lower = [-4 -4], upper = [4 4], ages = 30)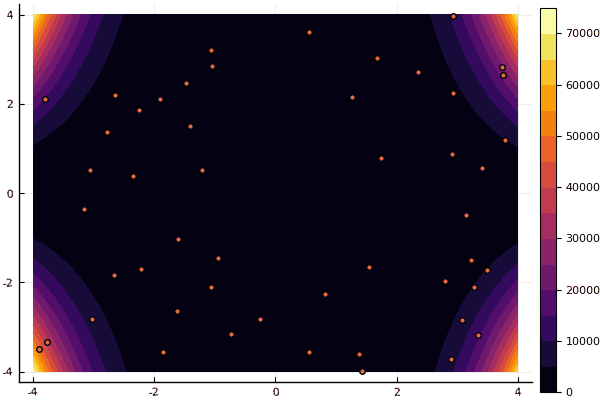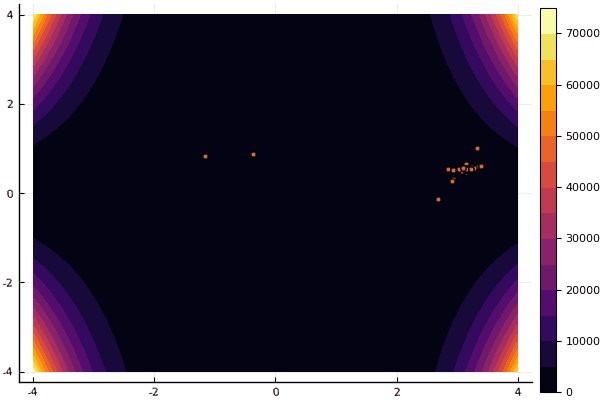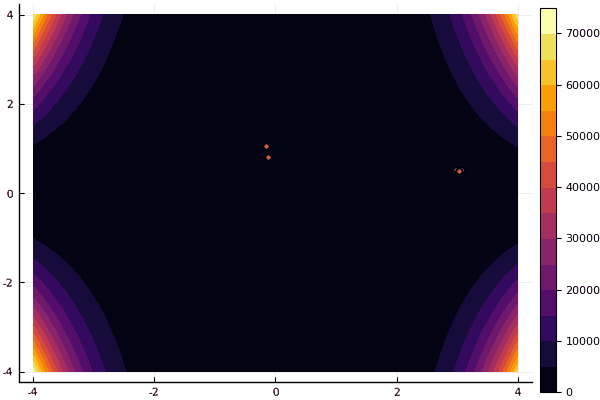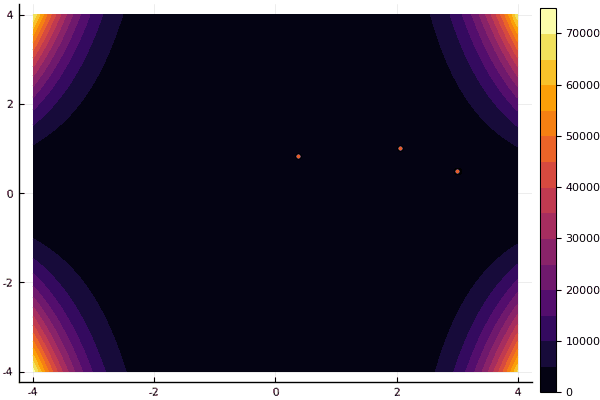

fun = ekly
mdpso(C1 = [1.7 1.7], C2 = [1.7 1.7], Ac = [0.07 0.07], lower = [-5 -5], upper = [5 5], ages = 15)

fun = himmelblau
mdpso(C1 = [1.1 1.1], C2 = [1.0 1.0], Ac = [0.09 0.09], lower = [-5 -5], upper = [5 5], ages = 20, parts = 50)

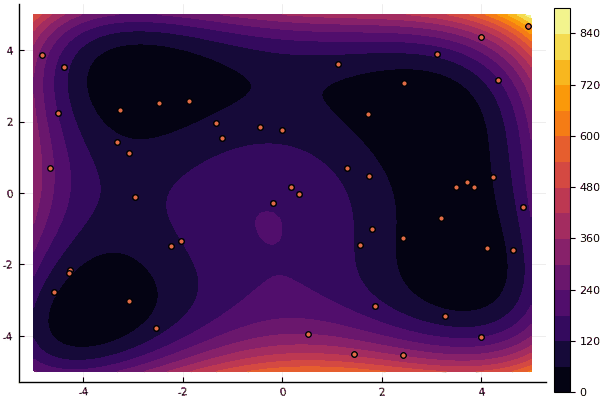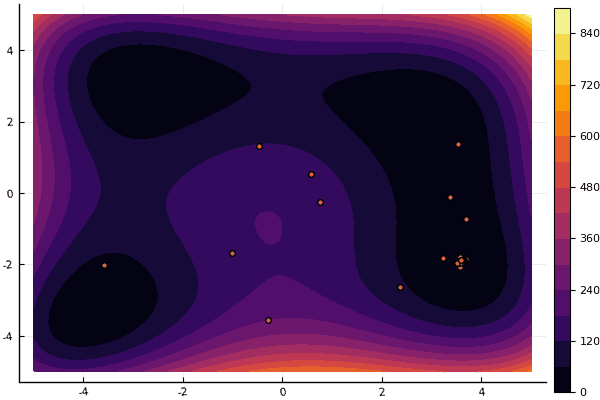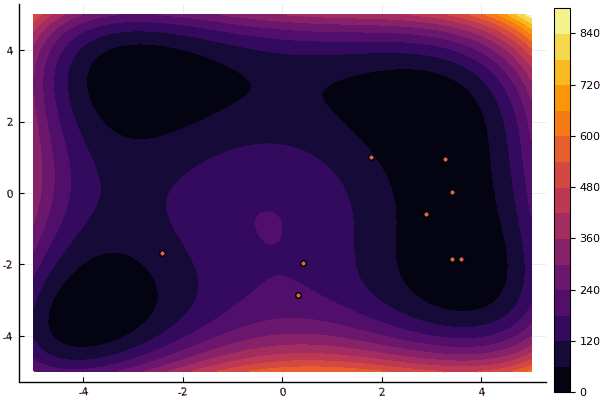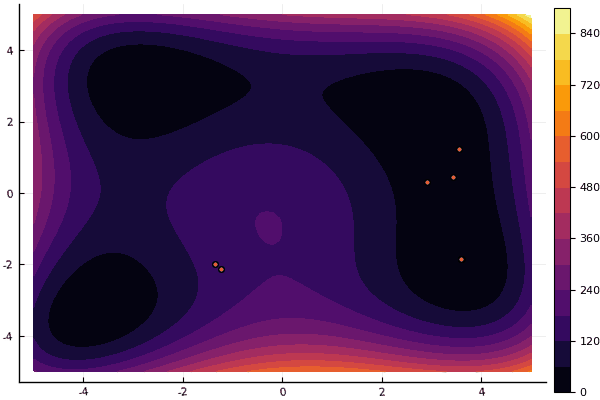
fun = holdertable
mdpso(C1 = [1.1 1.1], C2 = [1.0 1.0], Ac = [0.09 0.09], lower = [-10 -10], upper = [10 10], ages = 20, parts = 50)

fun = levy13
mdpso(C1 = [1.1 1.1], C2 = [1.0 1.0], Ac = [0.09 0.09], lower = [-10 -10], upper = [10 10], ages = 20, parts = 50)

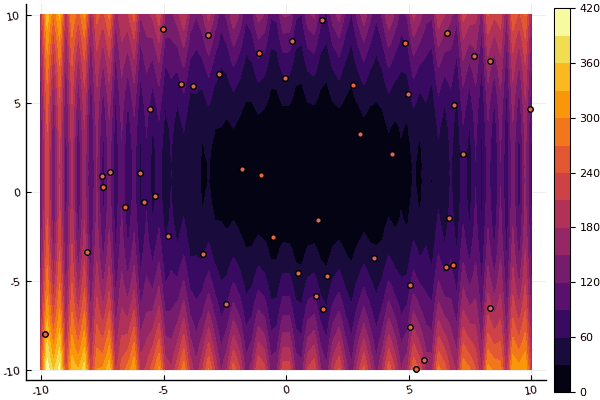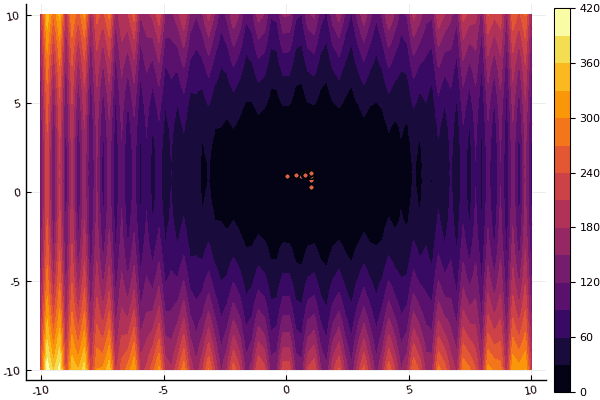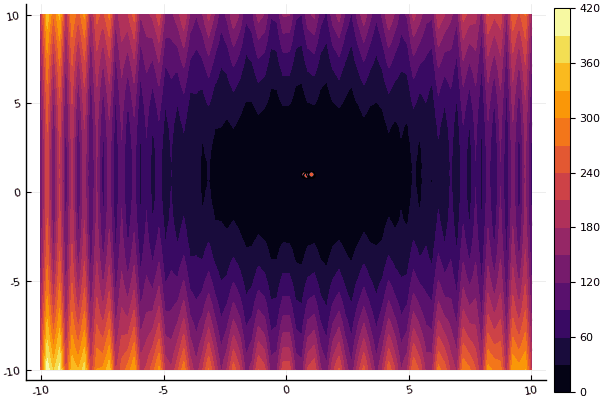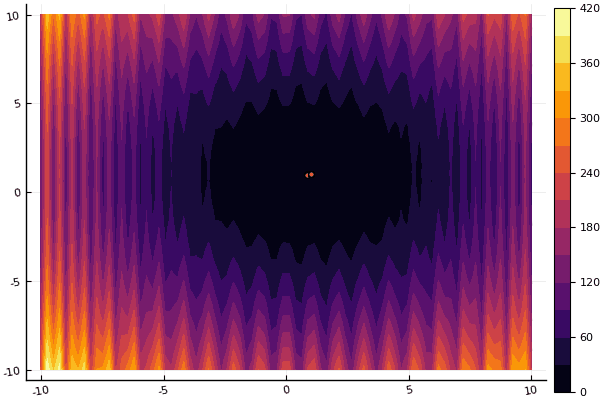
fun = shaffer4
mdpso(C1 = [1.1 1.1], C2 = [1.0 1.0], Ac = [0.09 0.09], lower = [-100 -100], upper = [100 100], ages = 20, parts = 50)

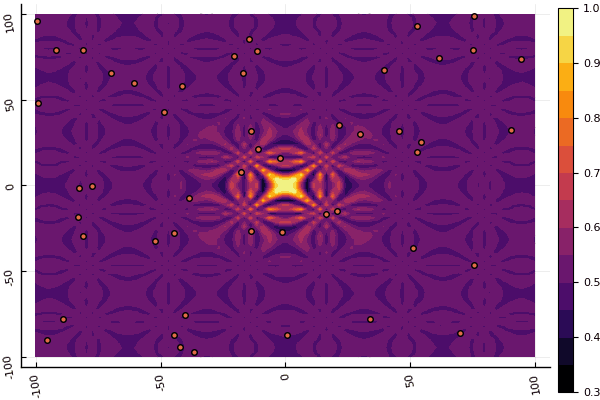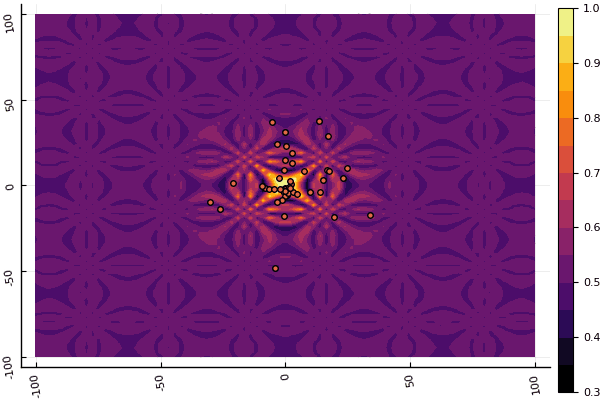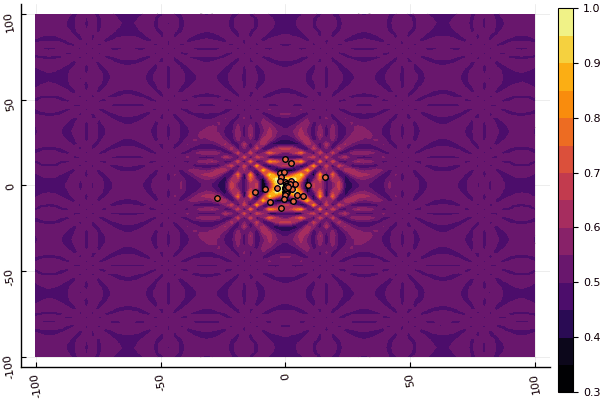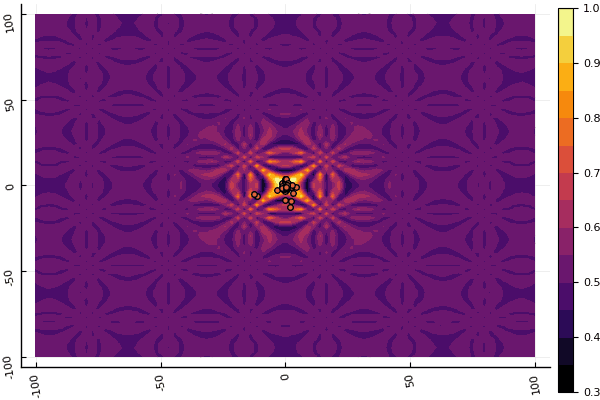
Что действительно удручает, так это возня с параметрами и элемент случайности: если возле глобального минимума не пролетела ни одна частица, то всё это дело может завалиться в локальный:

fun = rastrigin
mdpso(mdpso(C1 = [0.1 0.1], C2 = [1 1], Ac = [0.08 0.08], lover = low, upper = up, ages = 30))

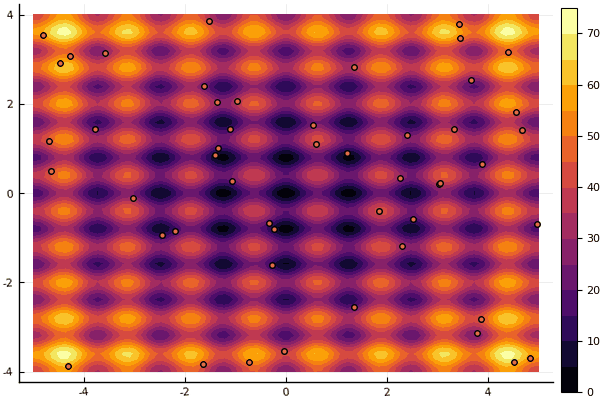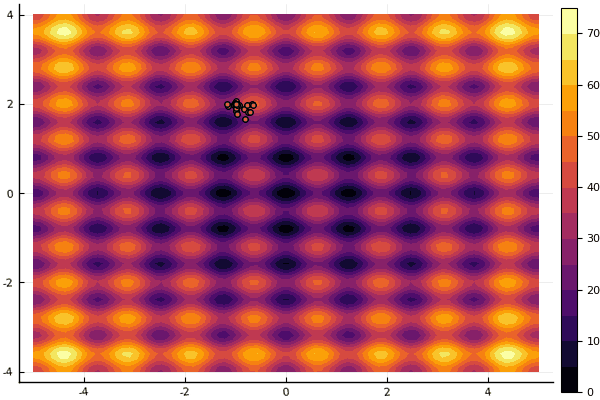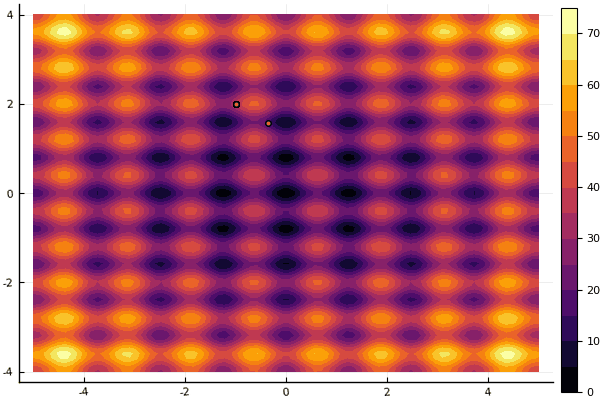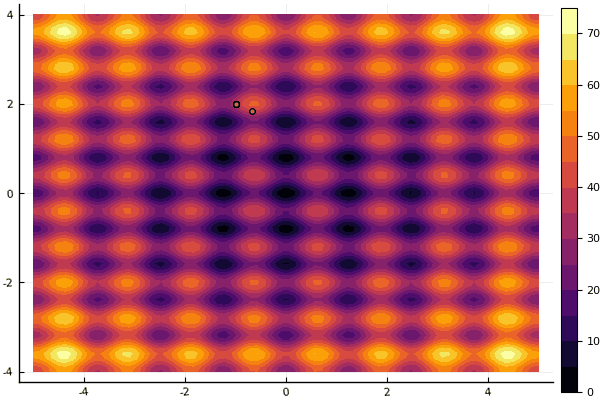
Да и старый не очень добрый Розенброк всё также не дает постигнуть себя:

fun = rosenbrok
mdpso(C1 = [1.7 1.7], C2 = [1.5 1.5], Ac = [0.15 0.15], lover = low, upper = up, ages = 20, nparts = 50)

...
Age № 20
 xbest:
 0.37796421341886866 0.12799160066705667
Fmin: 0.409026370833564

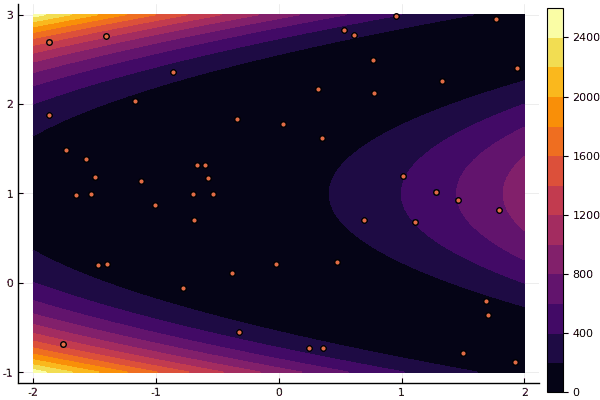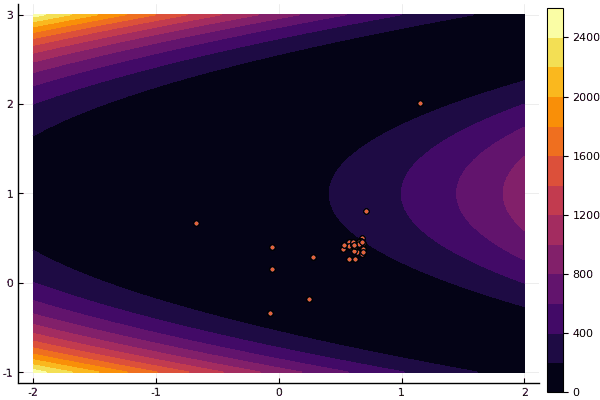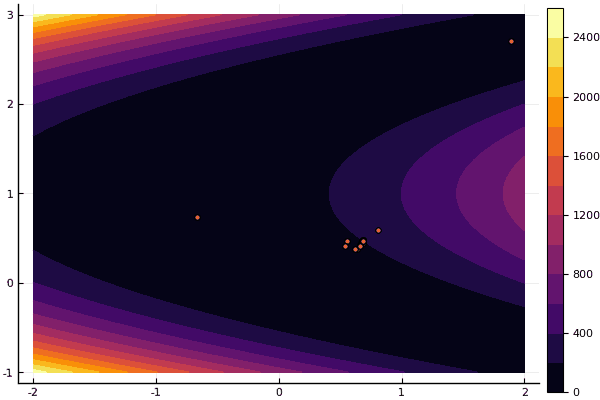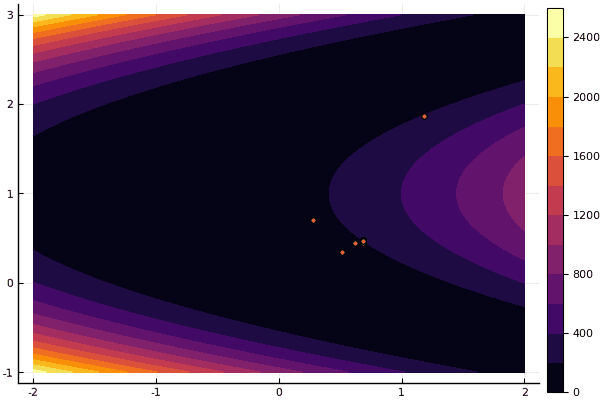
Но как я говорил ранее можно использовать МРЧ для поиска хорошего приближения к глобальному минимуму, а потом уж уточнять, скажем, Нелдером-Мидом:

vecl(x) = sqrt( sum(u -> u*u, x) )

function sortcoord(Mx)
    N = size(Mx,2)
    f = [fun(Mx[:,i]) for i in 1:N] # значение функции в вершинах
    Mx[:, sortperm(f)]
end

function normx(Mx)
    m = size(Mx,2)
    D = zeros(m-1,m)

    for i = 1:m, j = i+1:m
        D[i,j] = vecl(Mx[:,i] - Mx[:,j]) # считает длину разности столбцов
    end
    D
    sqrt(maximum(D))
end

function ofNelderMid(; ndimes = 2, ? = 1e-4, fit = [.1, .1], low = [-1 -1], up = [1 1])

    k = 0
    N = ndimes
    dz = zeros(N, N+1)
    Xx = zeros(N, N+1)

    for i = 1:N+1
        Xx[:,i] = fit
    end

    for i = 1:N
        dz[i,i] = 0.5*vecl(fit)
    end

    Xx += dz

    p = normx(Xx)

    while p > ?

        k += 1
        Xx = sortcoord(Xx)

        Xo = [ sum(Xx[i,1:N])/N for i = 1:N ] # среднее эл-тов i-й строки
        Ro = 2Xo - Xx[:,N+1]
        FR = fun(Ro)

        if FR > fun(Xx[:,N+1])
            for i = 2:N+1
                Xx[:,i] = 0.5(Xx[:,1] + Xx[:,i])
            end     
        else
            if FR < fun(Xx[:,1])

                Eo = Xo + 2(Xo - Xx[:,N+1])

                if FR > fun(Eo)
                    Xx[:,N+1] = Eo
                else
                    Xx[:,N+1] = Ro
                end
            else
                if FR <= fun(Xx[:,N])
                    Xx[:,N+1] = Ro
                else
                    Co = Xo + 0.5(Xo - Xx[:,N+1])

                    if FR > fun(Co)
                        Xx[:,N+1] = Co
                    else
                        Xx[:,N+1] = Ro
                    end
                end
            end
        end

        println(k, " ", p, " ", Xx[:,1])
        p = normx(Xx)

    end #while 

    fit = Xx[:,1]
end

ofNelderMid(fit = [0.37796 0.127992])

...
92 0.00022610400555036366 [1.0, 1.0]
93 0.00015987967588703512 [1.0, 1.0]
94 0.00011305200343052599 [1.0, 1.0]
2-element Array{Float64,1}:
 0.9999999996645973
 0.9999999995466575

Для классического МРЧ не всё ясно с критерием остановки: лучшая точка может держать позицию несколько эпох, расстояния между некоторыми частицами тоже могут длительное время не меняться. Поэтому используется ограничение на количество эпох. Чтоб повысить шансы нахождения глобального минимума нужно увеличивать количество частиц и эпох, что весьма затратно в плане памяти и, тем более, времени (Шутка ли, 50 вызовов целевой функции для каждой размерности на каждой итерации).

Мораль

• Если не хочется или не можется использовать сложные и современные методы, можно использовать композиции методов попроще
• Очень часто для задачи существует узкозаточенный метод (например для овражных функций)
• Желательно иметь под рукой несколько различных МО для последовательного сравнения
• Не всегда получается сунуть свою задачу в метод и сразу же получить правильный ответ — следует потратить время на исследование, варьирование параметров, если нет возможности просмотреть рельеф, то нужно хотябы распечатывать промежуточные вычисления, чтоб отслеживать сходимость.

На сегодня всё, спасибо за внимание и желаю всем хорошей оптимизации!