Виды бесконечностей и вынос мозга / forpes.ru

Главная
Виды бесконечностей и вынос мозга

Виды бесконечностей и вынос мозга +47

29.03.2019 11:46

Tzimie 151 17400 Источник

Эта статья — продолжение статьи про громадные числа. Но сейчас мы пойдем еще дальше — в бесконечности бесконечностей.

Для этого нам понадобится ZFC — теория множеств Zermelo, Frenkel + Choice. Choice — это аксиома выбора, самая спорная аксиома теории множеств. Она заслуживает отдельной статьи. Предполагается, что вы знаете, что такое «мощность» множества. Если нет, то погуглите, наверняка это изложено лучше, чем смогу я. Здесь я лишь напомню некоторые

Известные факты

Мощность множества целых чисел обозначается $\aleph_0$ . Это первая бесконечная мощность, такие множества называются счетными.
Мощность любого бесконечного подмножества целых чисел — простые, четные итд. — тоже счетна.
Множество рациональных чисел, то есть дробей p/q тоже счетно, их можно пройти змейкой.
Для любой мощности есть операция powerset — множество всех подмножеств, которая создает мощность бОльшую, чем исходная. Иногда эта операция обозначается как возведение двойки в степень, то есть $powerset(\aleph_0) = 2^{\aleph_0} = \aleph_c$ . powerset от счетной мощности есть мощность континуума.
Мощностью континуума обладают: конечные и бесконечные отрезки, плоские и объемные фигуры, и даже n-мерные пространства целиком
Для обычной математики следующая мощность, $powerset(\aleph_c)$ практически не нужна, обычно вся работа происходит со счетными множествами и множествами мощности континуума

Теперь

Малоизвестные факты

В ZFC не все собрания элементов могут быть множествами. Бывают коллекции столь широкие, что позволить им быть множествами нельзя, возникают парадоксы. В частности, "множество всех множеств" не есть множество. Впрочем, есть теории множеств, где такие множества разрешены.

Дальше. Теория множеств… Каких объектов? Чисел? Яблок? Апельсинов? Как ни странно, ZFС не нуждается ни в каких объектах. Возьмем пустое множество {} и договоримся, что оно означает 0. 1 обозначим с помощью {{}}, двойку как {{{}}} итд. {5,2} есть {{{{{{{}}}}}}, {{{}}}}. С помощью целых чисел мы можем создать вещественные, а коллекции вещественных создают любые фигуры.

Таким образом, теория множеств это… как бы сказать… пустотелая теория. Это теория ни о чем. Точнее, о том как можно нестить (nest, то есть вкладывать друг в друга) фигурные скобки.

Единственная операция, которая определена в теории множеств, это

$\in$ — символ принадлежности. А как же объединение, исключение, равенство итд.? Все это макросы, например:

$(A = B) \equiv \forall x((x \in A) = (x \in B))$

То есть, в переводе на русский язык, два множества считаются одинаковыми, когда при тестировании любого элемента на принадлежность к им мы будем получать одинаковые результаты

Множества не упорядочены, но это можно исправить: пусть упорядоченная пара (p,v) это {{p}, {p, v}}. Неэлегантно с точки зрения программиста, но достаточно для математика. Теперь множество всех пар param-value задает функцию, которая теперь тоже множество! Et voila! весь математический анализ, который работает на уровне языков второго порядка, так как говорит не о существовании чисел, а существовании функций — коллапсирует в язык 1 порядка!

Таким образом, теория множеств — это убогая теория без объектов и с одним значком отношения, которая обладает совершенно чудовищной силой — без каких то новых допущений она порождает из себя формальную арифметику, вещественные числа, анализ, геометрию и многое другое. Это своеобразное TOE математики.

Гипотеза континуума — CH

Существует ли мощность между

$\aleph_0$ и

$2^{\aleph_0}$ ? Это проблему не мог решить Кантор, «король математиков» Гильберт высоко оценивал ее важность, но лишь позже было доказано что эту гипотезу нельзя ни доказать, ни опровергнуть. Она независима от ZFC.

Это означает, что вы можете создать две разных математики: одну с ZFC+CH, другая ZFC+(not CH). На самом деле даже больше, чем две. Допустим, мы отвергнем CH, то есть будем верить, что между

$\aleph_0$ и

$2^{\aleph_0}$ есть еще мощности. Сколько их может быть? Одна, две? Гедель верил, что только одна. Но, как оказалось, предположение о том, что их 2, 17, 19393493 не приводит к противоречиям. Любое число, но не бесконечное!

Когда в формальной арифметике мы сталкиваемся с недоказуемым утверждением, то в силу определенных причин мы знаем, что, тем не менее, это утверждение, хоть и не доказуемо, но на самом деле либо истинно, либо ложно. В теории множеств это не работает, мы реально получаем разные математики. Как к этому относиться? Есть три философских подхода:

Формализм: а чему, собственно, удивляться? Мы задаем правила игры в символы, разные правила — разный результат. Не надо искать проблему там, где ее нет

Платонизм: Но как тогда объяснить, что совершенно разные теории, например ZFC и New Foundations, построенные по совершенно разным принципам, дают почти всегда один и тот же результат? Не говорит ли это о том, что за формулами стоит какая то реальность, которую мы изучаем? Такой точки зрения придерживался, например, Гедель

Multiverse: У нас может быть много аксиоматик, иногда дающих одинаковый результат, иногда нет. Мы должны воспринимать картину в целом — если с разными системами аксиом ассоциировать цвет, то цветное дерево следствий и есть математика. Если что-то верное везде — это белый цвет, но есть и цветные ветви.

Все выше и выше.

В дальнейшем мы, для простоты, примем гипотезу континуума, то есть

$powerset(\aleph_0) = \aleph_1 = \aleph_c$ — это очень удобно. На самом деле мы примем и более сильную аксиому, обобщенную гипотезу континуума, что между x и powerset(x) никогда нет промежуточных мощностей. Теперь мы итерируем powerset и все просто:

$\aleph_0 \rightarrow \aleph_1 \rightarrow \aleph_2 \rightarrow ... \rightarrow \aleph_{36463634} \rightarrow$

Как далеко мы можем продвинуться? После бесконечного количества итераций мы дойдем до

$\aleph_\omega$ — бесконечная по порядку мощность! Кстати, ее существование было неочевидно Кантору. Но секунду! Ведь функция powerset всегда определена, поэтому

$\aleph_\omega$ не может быть последней!

$\aleph_\omega \rightarrow \aleph_{\omega+1} \rightarrow \aleph_{\omega+2} \rightarrow ...$

Чтобы получить

$\aleph_{\omega+3}$ надо повторить powerset бесконечность и еще три раза. У вас уже начало сносить крышу? То ли еще будет. Потому что снова проитерировав powerset бесконечное число раз, мы дойдем до

$\aleph_{\omega+\omega} = \aleph_{\omega2}$ , после чего, естественно, идет

$\aleph_{\omega2+1}$

Дойдя до бесконечности бесконечное число раз, мы получим индекс

$\omega^2$ . Как вам такая мощность, например:

$\aleph_{\omega^3+\omega^2+\omega4+48745}$ ? Пока мы итерировали powerset по списку ординалов, вот начальные ординалы:

но их значительно, значительно больше. Так что мы сразу все это пропустим и сделаем

Сразу большой шаг

Внимание! То что написано дальше, может быть опасно для вашего мозга! Мы итерировали powerset счетное число раз, а не замахнуться ли нам на континуум? Честно, меня самого немного колбасит от того, что цикл может выполняться континуум раз, но теория множеств требует существования

$\aleph_{\aleph_1}$

Далее мы пойдем быстрее:

$\aleph_{\aleph_1} \rightarrow \aleph_{\aleph_2} ... \rightarrow \aleph_{\aleph_\omega} = \aleph_{\aleph_\aleph} \rightarrow$

У последнего алефа индекс ноль, но местный latex не дает его поставить — слишком много уровней. Но главное вы поняли, какую бы новую чудовищную мощность мы бы не создали, мы можем сказать — ага, это всего лишь повторитель, и поставить всю эту конструкцию к новому алефу в виде индекса. Теперь мощности растут как снежный ком, нас не остановить, пирамида алефов все выше, и мы можем создать любую мощность… Или нет?

Недостижимые мощности

Что если есть мощность настолько большая,

$\theta$ , что как бы мы ее ни пытались достичь «снизу», выстраивая конструкции из алефов, мы ее не достигнем? Оказывается, существование такой мощности независимо от ZFC. Вы можете принять ее существование или нет.

Я слышу шепот «бритва Оккама»… Нет, нет. Математики придерживаются противоположного принципа, который называется онтологический максимализм — пусть существует все, что возможно. Но существуют еще как минимум две причины, почему эту гипотезу хочется принять.

Во первых, это не первая недостижимая мощность, которую мы знаем. Первая… это всем знакомая счетная мощность. Как ни странно, она обладает всеми свойствами недостижимой — просто ее не принято так называть:
Бесконечную мощность никак не получить «снизу» — ни добавляя элементы конечное количество раз, ни итерируя powerset() конечное число раз, используя конечные множества для затравки, бесконечности вы не получите. Чтобы получить бесконечность, вы где-то должны уже иметь ее.
Существование бесконечной мощности вводится специальной аксиомой — аксиомой бесконечности. Без нее существование бесконечной мощности недоказуемо.

Второе: если отвергнуть аксиому бесконечности, то мы получим FinSet, простую игрушечную теорию множеств с конечными множествами. Давайте выпишем все эти множества (так называемая модель теории)

{}
{{}}
{{{}},{}}
{{{{}}}}
{{{{}}},{{}}}
{{{{}}},{{}}}
{{{{}}},{{}},{}}
…

И получим… бесконечное множество конечных множеств… То есть, модель теории конечных множеств бесконечна, и играет в ней роль «множества всех множеств». Может быть, это поможет понять, почему теория не может говорить о «множестве всех множеств» — такое множество всегда существует как модель вне теории и обладает другими свойствами, чем множества внутри. Вы не можете добавить в теорию конечных множеств бесконечное.

И да,

$\theta$ это «множество всех множеств» теории ZFC. В этом видео в конце очень красиво сказано про недостижимую мощность, но нам пора дальше.

Еще дальше.

Разумеется, мы моем пойти дальше, итерируя

$powerset(\theta)$ . Пройдя все описанные этапы, построив огромные башни повторителей, мы снова упремся в недостижимый кардинал (но теперь нам не нужны новые аксиомы, с аксиомой существования недостижимой мощности, которую мы только что добавили, это стало доказуемо). И снова и снова.

$\theta_0 \rightarrow \theta_1 \rightarrow \theta_2 \rightarrow ... \rightarrow \theta_{36463634} \rightarrow$

Заметьте, что теперь стрелка у нас имеет смысл не как выполнение функции Powerset(), а GetNextInaccessible(). В остальном все выглядит очень похоже, мы имеем:

$\theta_{\theta_1} \rightarrow \theta_{\theta_2} ... \rightarrow \theta_{\theta_\omega} \rightarrow \theta_{\theta_\theta} \rightarrow$

Теперь то мы точно достигнем чего угодно… Или нет?

Иерархия больших мощностей.

Да, с помощью GetNextInaccessible мы упремся уже в гипер-недостижимую мощность. Существование ее требует принять еще одну аксиому. Есть и гипер-гипер-недостижимые мощности. И так далее. Но есть и другие способы определять мощности, не только через недостижимость:

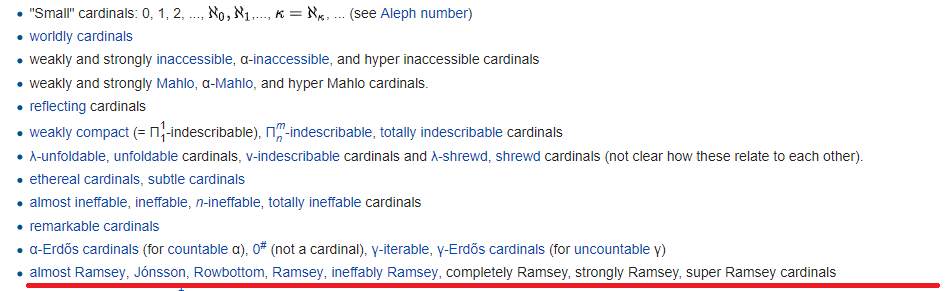
За каждой ссылкой стоит, как правило, целая бесконечная иерархия с произвольным количеством приставок hyper- и повторителей. Однако, общее количество формул, определяющие недостижимые кардиналы, не такое уж большое — ведь количество формул счетно!!! Поэтому рано или поздно они кончатся. Там, где они кончаются, проведена красная черта. Все, что ниже этой черты, определяется более зыбко, хотя и формально.

Сама красная черта обозначает конец вселенной Геделя (но не забываем, что Гедель создал ДВЕ разные вселенные) — вселенная множеств, конструируемых «снизу» с помощью формул. Мощности выше красной черты называются хм, «малыми», а ниже — большими:

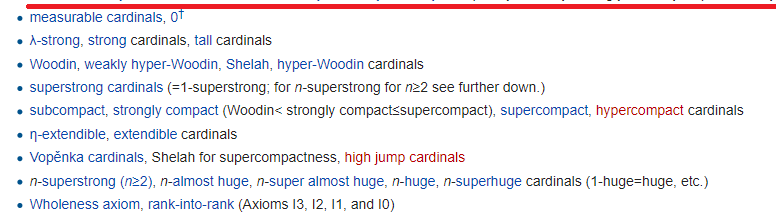
Главная идея в них в том, что вселенная множеств становится столь большой, что начинает повторять себя в разных смыслах. Каждая строчка, как всегда, требует отдельной аксиомы, и нескольких. И что еще интереснее, все это не настолько бесполезно, как вы могли подумать. Например, самая сильная аксиома (rank-into-rank), в самой нижней строчке, нужна, чтобы доказать факт о табличках.

Ниже опрос, последний вариант выбора расшифрован тут.

Комментарии (151)

SynteZZZ
29.03.2019 14:51
#19959644
www.youtube.com/watch?v=SrU9YDoXE88
1. Tzimie Автор
  29.03.2019 14:56
  #19959670
  Да, эта статья у меня упоминается
  1. SynteZZZ
    29.03.2019 15:07
    #19959738
    Эх, а ведь искал.

dedyshka
29.03.2019 15:05
#19959726
Не очень понятно, почему Формализм/Платонизм противопоставляется Multiverse?
1. Sychuan
  30.03.2019 01:52
  #19961790
  Тут не понятно причем тут мультиверс. Можно было бы и другие математические философии назвать. Интуицонизм, конструктивизм или что-то из современного.
  1. Tzimie Автор
    30.03.2019 10:10
    #19962214
    Про интуиционизм лучше говорить в связи с Аксиомоф Выбора и конструктивной математикой

irbisadm
29.03.2019 15:32
#19959852
www.youtube.com/watch?v=w-I6XTVZXww

KvanTTT
29.03.2019 15:54
#19960000
Для обычной математики следующая мощность, практически не нужна, обычно вся работа происходит со счетными множествами и множествами мощности континуума
Практически? А где все же нужна и как ее можно представить, может там какие-нибудь специальные числа. Например, при переходе от счетной к континуальной появились действительные числа.
1. Tzimie Автор
  29.03.2019 16:31
  #19960208
  См пример в конце, там ссылка на статью
1. 0xd34df00d
  30.03.2019 02:53
  #19961878
  Кстати, в обычной математике (вне анализа свойств континуума) вам нужны только вычислимые действительные числа, коих счетное число.
  1. Druu
    30.03.2019 14:22
    #19962784
    Кстати, в обычной математике (вне анализа свойств континуума) вам нужны только вычислимые действительные числа, коих счетное число.
    Чисел в принципе "счетное число", т.к. формул — счетное число. Можно доказать существование не более чем счетного числа объектов. Все остальные существуют только виртуально — вроде как у вас есть множество, которому эти объекты должны принадлежать, но сами эти объекты вы никак "пощупать" не можете, на самом деле их как бы и нет.
    
    Tzimie Автор
    30.03.2019 21:26
    #19963814
    На эту тему есть забавный парадокс: ru.wikipedia.org/wiki/%D0%9F%D0%B0%D1%80%D0%B0%D0%B4%D0%BE%D0%BA%D1%81_%D0%A1%D0%BA%D1%83%D0%BB%D0%B5%D0%BC%D0%B0
    
    Druu
    31.03.2019 09:33
    #19964626
    Я об этом и говорил. У нас просто есть некая интуиция "размера множества" и есть строгое понятие мощности. В конечных случаях определение совпадает с интуицией, и мы переносим этот факт автоматом на бесконечные случаи. Но бесконечные множества, в отличии от конечных, имеют внутреннюю структуру, которая может сохраняться либо нет. С-но, у нас может быть два неизоморфных (неравномощных), но одинаковых по размеру мн-ва (точно так же как может быть две одинаковых по размеру но неизоморфных группы).
1. SandroSmith
  02.04.2019 10:17
  #19972544
  Рискну предположить, что они нужны исключительно сумасшедшим (в хорошем смысле) математикам для получения докторских.
  Ну или просто для удовлетворения любопытства («а что, если...» и понеслось).
  1. KvanTTT
    02.04.2019 12:08
    #19973224
    Тут я даже не имел в виду какое-то практическое физическое применение (понятно, что его нет), а даже чисто теоретическое, что можно как-нибудь понять обычному человеку.
    
    Tzimie Автор
    02.04.2019 12:47
    #19973576
    Вот например johncarlosbaez.wordpress.com/2016/05/06/shelves-and-the-infinite

mwambanatanga
29.03.2019 17:17
#19960392
А существует ли бесконечность? Не бесконечная мощность множества, а просто бесконечное множество.
1. Tzimie Автор
  29.03.2019 17:28
  #19960438
  В теории ZFC — точно Да
  А вот у древних греков было другое мнение
1. Tzimie Автор
  29.03.2019 17:28
  #19960440
  del
1. alloky
  30.03.2019 10:42
  #19962290
  А в чём тут разница? Казалось бы если существует бесконечная мощность, то существует множество для которого оно является мощность.

deitry
29.03.2019 18:49
#19960770
Господи Иисусе. Ничего не понял, но это очень круто. Завидую людям, которые могут досчитать

до бесконечности бесконечное число раз
1. Deosis
  30.03.2019 14:16
  #19962770
  Элементарно, как в анекдоте про математиков.
  К зданию, в котором проходит конференция по математике, подъезжает автобус, из которого выходит бесконечное (счетное) количество математиков. И все они заходят в здание. Если нумеровать зашедших математиков, то здесь вы досчитали до бесконечности один раз.
  Далее, подъезжает ещё один автобус с математиками. Здесь остановился Чак Норрис.
  Далее, подъезжает бесконечное количество автобусов. Вот вы и досчитали бесконечное число раз до бесконечности (омега в квадрате)
  Проведите бесконечное количество конференций и получите омега в кубе.
  А вот представить степенную башню из омег, содержащую омега этажей, уже сложно.
  1. deitry
    30.03.2019 17:51
    #19963304
    Спасибо за пояснение, введение конкретного физического смысла позволило досчитать до бесконечности ещё раз.
    
    Проведите бесконечное количество конференций и получите омега в кубе.
    Теперь мощность моего воображения заканчивается здесь. :(
    Будет над чем помедитировать на досуге.
    
    maxzhurkin
    31.03.2019 07:38
    #19964506
    Но до мощности континуума так не добраться: математиков всё время мало :)
    
    chersanya
    31.03.2019 13:15
    #19965152
    Можно и до континнума: уже приехавшие математики стали собираться во всевозможные группы (подмножества), и каждая группа пригласила извне ещё одного математика.
    
    maxzhurkin
    01.04.2019 18:36
    #19970574
    Так тоже получится счётная мощность: континуальной мощностью будет обладать множество ВСЕХ подмножеств множества математиков, то есть, математикам придётся ещё бесконечное число раз перегруппироваться, и тогда, возможно (я в этом очень не уверен), множество всех групп за всё (!) время будет иметь мощность континуума
    
    chersanya
    01.04.2019 22:19
    #19971358
    Ну так я и пишу, что все возможные подмножества — как раз будет континуум.

rvt
29.03.2019 19:00
#19960798
Помню, еще в школе, классе в восьмом, задавался вопросом — каких чисел больше, кратных пяти или кратных десяти :)
1. amarao
  30.03.2019 13:07
  #19962568
  При том, что их число бесконечно, предел отношений (кратных 10 к кратных 5) будет 2.
  1. Hardcoin
    30.03.2019 20:41
    #19963720
    На любом отрезке числовой оси — да. Но если брать всю ось — то их одинаково. Все счётные множества имеют одинаковое количество элементов.
    
    amarao
    30.03.2019 23:16
    #19964022
    -1
    Вы же понимаете, что когда вы говорите «количество», вы же не про натуральные числа говорите, а про дурацкие трансфинитивные конструкции, всё существование которых зависит от ~~религиозных убеждений~~ спорных аксиом.
    
    А я говорю про старый-добрый предел, в котором бесконечность — только возле стрелочки. И если религиозные представления запрещают писать =?, то устремляться — всегда пожалуйста. «Для любого эпсилон есть такая сигма, что...» и т.д.
    
    mayorovp
    30.03.2019 23:49
    #19964102
    Пределы и все вот эти стрелочки основаны, в том числе, на теории множеств и всех этих построениях. Так что сравнивать «дурацкие трансфинитные конструкции» со «старым добрым пределом» — некорректно.
    
    Что же до предмета спора, то математически корректно будет сказать, что чисел кратных пяти столько же, сколько и кратных десяти, но встречаются они в два раза чаще.
    
    maxzhurkin
    01.04.2019 18:39
    #19970590
    Ну, математически корректно будет формально математически описать термин «встречается», прежде (не в буквальном смысле, можно и после) чем его использовать
    
    amarao
    02.04.2019 11:16
    #19972888
    Стоп. А чему равен предел count5(n)/count10(n) при n >??
    
    red75prim
    02.04.2019 12:31
    #19973406
    2. Но почему именно count5(n)/count10(n)? Мы же считаем не отношение частоты с какой они встречаются, а их количество. Пусть a_i = i*5, b_i = i*10, количество элементов с i < n, в этих последовательностях одинаково. Предел отношения этих количеств при n >? соответственно равен 1.
    
    amarao
    02.04.2019 12:52
    #19973606
    А почему у вас в качестве счётчика используется собственный порядковый номер, т.е. почему мы их считаем раздельно?
    
    mayorovp
    02.04.2019 13:31
    #19973830
    Потому что можем. Нет никаких причин «выравнивать» последовательности при подсчете количества строго определенным способом.
    
    Количество элементов в множестве как бы не должно зависеть от порядка в котором мы их подсчитываем, иначе это уже не количество.

vics001
29.03.2019 20:15
#19961088
+1
Как далеко мы можем продвинуться? После бесконечного количества итераций мы дойдем до — бесконечная по порядку мощность! Кстати, ее существование было неочевидно Кантору. Но секунду! Ведь функция powerset всегда определена, поэтому не может быть последней!

Думаю многим и сейчас неочевидно, почему функция определена везде? Почему ее можно применить после бесконечного числа раз и самый главный вопрос, почему для после бесконечного числа итераций они вдруг не начнут совпадать, то есть операция powerset — просто не замкнется. Разве это все выражается в ZFC?
1. Tzimie Автор
  29.03.2019 20:17
  #19961096
  +2
  >почему для после бесконечного числа итераций они вдруг не начнут совпадать, то есть операция powerset — просто не замкнется
  
  Это доказано еще Кантором
  1. vics001
    30.03.2019 15:02
    #19962896
    Доказано, используя теорию множеств. Для классов и для таких множеств нужны другие аксиомы.
    
    Tzimie Автор
    30.03.2019 21:24
    #19963808
    powerset применим к множествам.
    для собственных классов это разумеется не работает
    Например, если V — вселенная (класс всех множеств), то powerset(V) = V
    именно поэтому собственные классы не множества — чтобы не было парадоксов
    
    Но в статье мы не дошли до собственных классов

jcmvbkbc
29.03.2019 23:24
#19961550
+2
С помощью целых чисел мы можем создать вещественные

Мне кажется, что из этой фразы следует эквивалентность множеств целых и вещественных чисел, что, как известно, неверно.
1. Sayonji
  31.03.2019 09:56
  #19964666
  В статье говорится об операции powerset, которая как раз превращает рациональные в вещественные.

ThisMan
29.03.2019 23:44
#19961598
+1
Честно прочитал все полностью
Честно ничего не понял
Добавил в закладки, что бы потом снова прочитать и снова ничего не понять
И так N + 1 раз, где N бесконечность

vintage
29.03.2019 23:48
#19961610
-2
Тут неплохо показано, что никаких несчётных множеств нет и быть не может: habr.com/ru/post/445762
1. Sychuan
  30.03.2019 01:54
  #19961794
  +2
  ничего такого там не показано. Если вам не нравятся несчетные множества, то придется отказаться от вещественных чисел. И я боюсь, что в этом случае сломается анализ.
  1. vintage
    30.03.2019 07:19
    #19962028
    Вы внимательно почитайте. И вспомните «доказательство» несчётности.
    
    playermet
    30.03.2019 13:43
    #19962670
    Счетное множество это то, у которого существует биекция со множеством натуральных чисел. У иррациональных чисел, которые часть вещественных, такой биекции не существует.
    
    vintage
    30.03.2019 14:05
    #19962744
    -1
    Даже с уверенностью повторённая глупость меньше глупостью не становится.
    
    playermet
    30.03.2019 15:53
    #19963034
    Будут какие-то конструктивные аргументы, а не утверждения что мои аргументы глупые?
    
    vintage
    30.03.2019 18:00
    #19963328
    -2
    Вы используете выводы из неверного доказательства в качестве обоснования, что доказательство верно.
    
    Cerberuser
    30.03.2019 19:22
    #19963500
    +1
    Вам удастся высказаться конкретнее (какой вывод и из какого доказательства был приведён), или нам требуется угадывать Вашу мысль самостоятельно?
    
    playermet
    30.03.2019 20:48
    #19963732
    +1
    Укажите пожалуйста конкретную ошибочную строчку в тексте доказательства, с развернутым пояснением почему она не верна.
    
    vintage
    30.03.2019 22:27
    #19963926
    -2
    Ну, приведите тогда для начала вашу любимую формулировку доказательства.
    
    Cerberuser
    31.03.2019 06:40
    #19964474
    Зачем приводить «любимую», если можно привести ту, которую Вы и сами моментально нашли бы, если бы считали нужным спорить, а не упираться рогом? ru.wikipedia.org/wiki/%D0%94%D0%B8%D0%B0%D0%B3%D0%BE%D0%BD%D0%B0%D0%BB%D1%8C%D0%BD%D1%8B%D0%B9_%D0%B0%D1%80%D0%B3%D1%83%D0%BC%D0%B5%D0%BD%D1%82
    
    vintage
    31.03.2019 08:49
    #19964590
    Я знаю как минимум несколько формулировок. Даже по ссылке вашей в названии фигурирует диагональный аргумент, картинка про диагональный аргумент, а в тексте про диагональный аргумент, собственно, ни слова. Так какой вариант будем разбирать? Диагональный или Множественный?
    
    Cerberuser
    31.03.2019 08:53
    #19964598
    Тот, про который Вы сказали чуть выше, что вывод из него используется в словах собеседника. Неужели так трудно развивать свою собственную мысль?
    
    vintage
    31.03.2019 09:50
    #19964646
    -1
    Без разницы они все имеют одну и ту же логическую ошибку — самоотрицание.
    
    mayorovp
    31.03.2019 11:04
    #19964814
    Это называется не «самоотрицание», а «рассуждение от противного». Которое допустимо благодаря закону исключённого третьего.
    
    vintage
    31.03.2019 15:20
    #19965430
    -1
    Рассуждение от противного работает только для одного единственного предположения. Тут же вводятся 2, которые изначально противоречат друг другу:
    
    Для любого а из А есть ровно один б из Б, и наоборот.
    
    Существует такой а из А, который не равен любому соответствию б из Б в А.
    
    А из противоречивых утверждений, как известно, можно сделать совершенно любые выводы. Кантор, в частности, решил, что (2) несомненно, а следовательно (1) ложно. Но с тем же успехом можно прийти и к противоположным выводам.
    
    mayorovp
    31.03.2019 15:41
    #19965472
    Второе не вводится, а строится как следствие первого.
    
    vintage
    31.03.2019 16:18
    #19965524
    -1
    Вводится в той же мере, что и «брадобрей бреющий всех и только тех, кто не бреет себя сам». Не всё, что можно сформулировать, может существовать.
    
    Cerberuser
    31.03.2019 17:36
    #19965680
    +1
    А можно было сразу сказать, что Вы — сторонник конструктивной математики и отвергаете все теории, не приводящие к явному построению искомого объекта? Это бы сильно упростило нам жизнь, полагаю.
    
    vintage
    31.03.2019 18:41
    #19965820
    -1
    Я отвергаю лишь те теории, которые строятся на самоотрицании. И по ссылке, что я дал, человек размышляет о том, почему объявление противоречивых сущностей пагубно для математики. а против неконструктивных объявлений я ничего не имею. Если доказана их непротиворечивость. Аналогично предел ряда существует лишь если доказана его сходимость.
    
    Cerberuser
    01.04.2019 05:58
    #19966808
    А Вас не смущает, что доказательство от противного — это в точности Ваши рассуждения, только с одним дополнительным шагом: «а если для чего-то доказана его противоречивость, значит, оно неверно»?
    
    vintage
    01.04.2019 10:52
    #19967712
    -1
    А вы считаете этот шаг несущественным?
    
    mayorovp
    01.04.2019 11:03
    #19967778
    Нет, это вы почему-то считаете его несущественным и пропускаете при чтении доказательств.
    
    Druu
    31.03.2019 20:31
    #19966016
    Но с тем же успехом можно прийти и к противоположным выводам.
    Нельзя, т.к. 2 напрямую следует из аксиоматики.
    
    vintage
    01.04.2019 10:47
    #19967696
    -1
    Если вы про аксиому выбора, то она как ничто другое хорошо иллюстрирует то, что некоторые так сказать математики предпочитают изучать невидимых розовых единорогов, вместо того, чтобы заняться чем-то полезным.
    
    Фактически она постулирует, что (2) истина и поэтому (1) ложно. Но с тем же успехом можно было бы постулировать и что (1) истина, из чего следовала бы ложность (2).
    
    Вот вам самим что кажется более правдоподобным, что можно принять за базис рассуждений:
    
    Отсутствие чего-то не может быть больше или меньше отсутствия чего-то ещё.
    
    Всё, что можно описать, может существовать.
    
    Cerberuser
    01.04.2019 11:49
    #19968054
    Оба высказывания достаточно правдоподобны, за исключением того, что первое излишне запутано, а второе относится к элементам некоторой научной системы, а не конкретным физическим объектам.
    
    vintage
    01.04.2019 12:25
    #19968328
    «То, что существвоать не может» может существовать? Очень правдоподобно.
    
    Cerberuser
    01.04.2019 13:08
    #19968610
    Это не описание. Это одно конкретное свойство. Если Вы сможете привести полное (с опорой на некоторую аксиоматику) непротиворечивое описание сущности, которая обладает этим свойством, — разговор будет другой.
    
    vintage
    01.04.2019 13:52
    #19968860
    +1
    непротиворечивое
    Ключевой момент.
    
    Cerberuser
    01.04.2019 14:49
    #19969246
    Да, разумеется. Сущность, которой одновременно приписываются два несовместимых свойства (что и есть противоречие), существовать не может. Если у Вас есть пример обратного — прошу его предъявить.
    
    vintage
    01.04.2019 15:54
    #19969642
    -1
    Как вы ловко пересели на другой стул. На этом закончим.
    
    Druu
    01.04.2019 17:19
    #19970072
    +1
    Если вы про аксиому выбора
    Я в общем про ZFC.
    
    Вот вам самим что кажется более правдоподобным, что можно принять за базис рассуждений:
    Ни первое, ни второе. Есть аксиомы, есть правила вывода. Если формула, содержательно утверждающая существование чего-либо, выводится в рамках данной системы — то она выводится. Если не выводится — то не выводится. Но все это не совсем важно, поскольку:
    
    теорема Кантора утверждает как раз НЕсуществование определенного объекта. Конкретно — биекции между множеством и его булеаном. А существование утверждает как раз тот, кто говорит что такая биекция есть (или, что эквивалентно — несчетных множеств не бывает).
    
    Никакой аксиомы выбора для доказательства теоремы Кантора не требуется. Достаточно только аксиомы булеана и аксиомы выделения, без которых (или их содержательных аналогов) никакой вменяемой теории множеств просто нельзя построить
    
    исходя из вышесказанного — у вас каша в голове
    
    vintage
    01.04.2019 18:13
    #19970402
    -1
    Теорема Кантора утверждает именно **существование** такого объекта в бесконечном множестве, который не равен любому элементу этого же множества.
    
    Прям секта свидетелей Кантора какая-то. Впрочем, не буду учить вас жить. Вы имеете полное право верить в любой бред.
    
    Cerberuser
    01.04.2019 18:23
    #19970476
    Теорема Кантора утверждает именно **существование** такого объекта в бесконечном множестве, который не равен любому элементу этого же множества.
    
    А значит, этот элемент обладает двумя несовместимыми свойствами. Значит, он на самом деле не существует. Далее применяем метод «от противного»: существование выводилось из предположения, что множество и его булеан равномощны. Но существование невозможно, значит, и равномощность невозможна. Вам настолько не нравится метод «от противного», что Вы такими сложновывернутыми методами пытаетесь показать его некорректность?
    
    Druu
    02.04.2019 08:24
    #19972176
    Теорема Кантора утверждает именно существование такого объекта в бесконечном множестве, который не равен любому элементу этого же множества.
    Нет, не утверждает. Она вообще ничгео не утверждает про элементы бесконечных мн-в. Теорема кантора утверждает, что если у вас есть два непустых множества X и 2^X, то между ними не существует биекции.
    Вы же утверждаете, что биекция между ними есть. Или вы утверждаете, что нету самого мн-ва 2^X?
1. red75prim
  30.03.2019 08:43
  #19962080
  +2
  Вот это?
  
  Представим множество (или же список, массив) всех положительных целых чисел, а затем представим число, соответствующее количеству чисел в нашем множестве. Представили? Если да, то что будет со множеством после добавления в него числа, равного количеству его элементов с прибавленной единицей? Если там уже есть все элементы, вспомним, что они могут быть отсортированы по возрастанию и тогда станет очевидным, что наибольший элемент равен количеству элементов в нашем множестве. Но если прибавить к количеству единицу, то мы получим элемент, которого в множестве нет, значит вроде бы представить такой список нельзя, ведь каждый раз будет всплывать вопрос о новом элементе.
  Ошибка тут в том, что во множестве всех натуральных чисел нет максимального элемента. А значит нет и натурального числа равного количеству элементов во множестве натуральных чисел. Кроме того в вышеприведенном рассуждении смешиваются ординальные и кардинальные числа.
  
  До Кантора в девятнадцатом веке и ранее это было бы простительной ошибкой. Сейчас это — недостаток знаний.
  
  Аксиоматическое введение трансфинитных чисел и алефов не приводит к противоречиям. Можно сказать: "Я не верю в актуальные бесконечности", и отвергнуть аксиому существования бесконечных множеств, как делают финитисты, но доказать несуществование бесконечных и несчетных множеств не получится.
  1. vintage
    30.03.2019 11:07
    #19962340
    Вот это?
    Не это, продолжайте чтение :-)
    
    Я не верю в актуальные бесконечности", и отвергнуть аксиому существования бесконечных множеств
    Какой интересный переход. Уверен, вы в курсе термина "потенциальная бесконечность".
    
    но доказать несуществование бесконечных и несчетных множеств не получится.
    В той же мере, что и доказать, что бога нет.
    
    red75prim
    30.03.2019 11:36
    #19962390
    > Не это, продолжайте чтение
    
    Мне неинтересно играть в угадайку. Покажите где там вывод противоречия из аксиом Цермело — Френкеля или что-то аналогичное. Я ничего похожего там не увидел.
    
    vintage
    30.03.2019 13:32
    #19962624
    Не гадайте, а прочитайте. Вся статья о том, что «доказательство» несчётсности ничего не доказывает.
    
    Sayonji
    31.03.2019 07:33
    #19964500
    Я считаю, что играться с формальной логикой — хорошее занятие, строить теории и тому подобное — весело и полезно для ума. А вот приходить в чужие статьи и троллить — плохое занятие, единственный выхлоп это потраченные человеко-часы.
    
    vintage
    31.03.2019 08:51
    #19964592
    Ага, назови оппонента троллем и можно смело игнорировать его аргументы.
    
    Sayonji
    31.03.2019 09:46
    #19964638
    Какие еще аргументы? Вы лишь отсылаете к статье, в которой даже нет вхождний слова «счетное».
    В треде же чуть выше, где вам дали ссылку на доказательство Кантора и попросили указать ошибку (что было бы, вероятно, самым эпичным событием в математике за тысячу лет), вы пишете, что там картинка неправильная, т. е. троллите.
1. Hardcoin
  30.03.2019 20:46
  #19963728
  Как вы сделали такой странный вывод из этой статьи?
  1. vintage
    30.03.2019 22:30
    #19963932
    -2
    Ничего странного, если вспомнить как доказывается несчётность.
    Спойлер: точно так же.

Onigiri
30.03.2019 00:38
#19961706
+1
Меня как раз интересовал вопрос: если у нас есть гипотеза, которую можно опровергнуть контрпримером, и мы доказываем её недоказуемость, что значит, что контрпример привести невозможно, будет ли это означать её истинность? В статье вроде говорится, что с континуум-гипотезой так нельзя, а может ли такое быть например с гипотезой Римана?
1. Tzimie Автор
  30.03.2019 10:06
  #19962206
  Как я понимаю, такое работает только для счетных множеств. Если недоказуемо, что forall x A(X) значит контрпримера нет, значит это утверждение истинно на самом деле. Если же взять его отрицание как аксиому, то формально это не приведет к противоречиям, но такая арифметика будет w-противоречивой, что на бытовом уровне очень плохое свойство
  
  Почему это не работает для ZFC, это хороший вопрос. Мне самому надо подумать. По моему потому что и так в любой ветке ZFC уже неконструктивна (в математическом смысле) какие аксиомы или их отрицания не добавляй (например, попытка отказаться от Axiom of Choice заменой ее на Axiom of Determinancy избавляет от одних парадоксов, но добавляет свои)
  
  ЧТо касается вещественных чисел — то это зависит от того, как их вводить. Но скорее всего их можно вводить либо формально через ZFC, либо с помошью разного рода правдоподобных рассуждений, что ставит нас на зыбкую почву теорий второго порядка?
1. 0xd34df00d
  30.03.2019 16:58
  #19963162
  Если я правильно понял вопрос, то если гипотеза — тип Hyp, контрпример — тип Hyp > ?, доказательство невозможности контрпримера — тип (Hyp > ?) > ?, то ваш вопрос экивалентен наличию аксиомы о двойном отрицании в вашей логической системе.
  
  Правда, ещё под ковёр заметается вопрос о том, что такое «доказать недоказуемость».
  1. DjSapsan
    31.03.2019 00:08
    #19964152
    «Это утверждение недоказуемо» Это утверждение недоказуемо.
    
    0xd34df00d
    31.03.2019 01:44
    #19964314
    Это не формулировка на языке, например, FOL.
1. mayorovp
  31.03.2019 00:26
  #19964178
  Для того, чтобы это было так, нужно чтобы из существования контрпримера следовала доказуемость его существования. А это не так даже для гипотезы Римана: на множестве комплексных чисел континуум точек, но только счётное число точек является вычислимым. Все остальные точки мы не можем записать аналитически, а значит их нельзя использовать как контрпример в доказательстве.
  1. DjSapsan
    31.03.2019 01:02
    #19964258
    К сожалению не могу найти цитату. Читайте «I am a strange loop» Дугласа Хофштадтера, там много мозговыносящих примеров и разбор всех последних математических тем на хабре. Более популярно также разобрано в «Гёдель Эшер Бах»
  1. Druu
    31.03.2019 09:43
    #19964634
    Для того, чтобы это было так, нужно чтобы из существования контрпримера следовала доказуемость его существования.
    А "существование контрпримера" — это что? Не совсем понятно, как можно говорить о том, что что-то существует, если существование не доказано. В каком тогда смысле оно существует?

youyou2020
30.03.2019 02:24
#19961842
-2
Очередной математический пук
1. amarao
  30.03.2019 13:12
  #19962578
  Ага. И зачем вы его тут сделали?

0xd34df00d
30.03.2019 02:56
#19961884
Это своеобразное TOE математики.
Ну так себе TOE. В тру TOE утверждения типа $5 \in \sin$ не имеют смысла «статически», а в ZFC они просто ложны.

olegchir
30.03.2019 03:06
#19961892
Как же офигенно интересно вы, математики, живёте. Если вам ещё и платят за такое, я даже не знаю, это как-то нечестно :)
1. Tzimie Автор
  31.03.2019 19:26
  #19965894
  Да, вот это жизнь!
  ru.wikipedia.org/wiki/%D0%AD%D1%80%D0%B4%D1%91%D1%88,_%D0%9F%D0%B0%D0%BB
  Лучше прочтите по англ полный вариант, как он приезжал к знакомым математикам, говорил «мой разум открыт» и его кормили, а потом он предлагал назвать ему, куда ехать дальше… И все его имущество состояло из чемоданчика…
  
  Единственное, почему бы я не хотел поменяться с ним судьбой — у него вроде не было женщин.

Cerberuser
30.03.2019 09:37
#19962150
И всё-таки, множеством всех подмножеств какого множества является алеф-омега? Объединения всех множеств алеф-n при натуральных n (используя тот факт, что множество всех подмножеств включает в себя одноэлементные подмножества, а их множество эквивалентно исходному), или тут какая-то другая конструкция?
1. Tzimie Автор
  30.03.2019 09:47
  #19962160
  Пределом последовательности -> powerset() ->…
  Поэтому сам ординал omega называется предельным (limit ordinal)
1. red75prim
  30.03.2019 09:58
  #19962190
  Насколько я понимаю — никакого. По-моему, тут всё аналогично множеству натуральных чисел и операции прибавления единицы. Прибавляя единицу к натуральному числу мы никогда не выйдем за пределы множества натуральных чисел. Поэтому аксиоматически вводится трансфинитное число ?, которое располагается после всех натуральных чисел.
1. Deosis
  30.03.2019 14:02
  #19962732
  Допустим, множество мощности алеф-нуль — это множество чисел. Тогда алеф-1 состоит из множеств и содержит {}. Далее, {{}} не лежит в алеф-1, но лежит в алеф-2. Тогда {{...{{{}}}...}} (пропущено бесконечное количество скобок) лежит в алеф-омега и не лежит ни в каком предыдущем.

trofimovep
30.03.2019 09:47
#19962162
А какие принципиальные отличия между первым ординалом \omega и \omega + 1? Насколько я помню там это не очень понятно… И как я понимаю там в это опирается чуть ли нахождение гомотопических групп сфер, ну и если разница существенная, то ко всем доказательствам по индукции нужно доблавлять, что действительно до первого ординала))
1. Tzimie Автор
  30.03.2019 09:48
  #19962166
  omega это limit ordinal, в частности, нет такого ординала, которые ему предшествует
  omega+1 это successor ordinal, и он имеет предыдущий ординал — это, очевидно, omega
  ординалы бывают двух видов: limit and successor
1. 0xd34df00d
  30.03.2019 17:01
  #19963172
  Принципиальные отличия в том, что есть биекция, но нет изоморфизма. Если тот нолик справа, который даёт единицу в \omega + 1, изоморфизмом мапится на какой-то элемент в \omega, например, x, то x — 1 обязан мапиться на \omega-часть \omega + 1, а между этим отображением и нулём бесконечно много элементов, которые мы уже никуда замапить не можем.
1. Sayonji
  31.03.2019 10:15
  #19964700
  Как минимум в омега+1 есть наибольший элемент, а в омега нету.

shinzui
30.03.2019 09:49
#19962168
А где же сюрреальные числа, которые, по-моему, прекрасно описывают все эти бесконечные бесконечности, но совершенно не выносят мозг?
1. Tzimie Автор
  30.03.2019 09:53
  #19962172
  Surreal numbers это очень красивое построение, но у этих чисел есть страшный дефект. Так как поколения индексируются ординалами, а Ord — класс всех ординалов слишном широк и не является множеством, то коллекции surreal numbers — это собственные классы а не множества.
  
  так что вы, например, не можете взять множество surreal numbers между 1 и 3 и пересечь с множеством surreal numbers между 2 и 4

Num
30.03.2019 12:39
#19962506
А что насчёт кардиналов, не совместимых с аксиомой выбора?
1. Tzimie Автор
  30.03.2019 21:15
  #19963792
  Спасибо за вопрос
  
  Да такие есть на самом верху… И что интересно, в New Foundations, построенной по совсем другим принципам:
  1. Существует «множество всех множеств»
  2. Аксима выбора опровергается в New Foundations
  3. New foundations «из коробки» дает ZFC + начальные расширения недостижимых кардиналов
  4. Для всех множеств, ограниченых какой то очень большой (недостижимой) мощностью в New Foundations аксиома выбора НЕ опровергается
  
  То есть, NF повторяет ZFC+расширения (совпадение? не думаю) и обе теории говорят, что AC не верна, но для очень очень очень больших мощностей. Платонист во мне говорит, это это показывает нам, что мы реально изучаем некую реальность, а это не игра в символы

Poft
30.03.2019 13:34
#19962630
В статье не раскрыта тема бесконечного взятия powerset.

Если интересно, советую посмотреть «Не совсем наивная теория множеств» Вавилова. Она написана в непривычно художественном стиле, но доказательства строгие.
1. Tzimie Автор
  30.03.2019 21:22
  #19963798
  +1
  Хм. Я старался
  А как же мы досчитали до aleph_omega, aleph_aleph_0 итд?

olekl
30.03.2019 15:11
#19962926
Пишите еще! Интересно! :)

DjSapsan
30.03.2019 21:37
#19963838
Меня волнует один вопрос.
Машина Тьюринга это конечный автомат с бесконечной лентой. Но на эту ленту можно записать только конечный алгоритм. И никакое выполнение алгоритма не может занять всю ленту.
Итак, всякий компьютер реализует машину Тьюринга. Но логически всякий компьютер является конечным автоматом. Хотя, если учитывать, что Машина Тьюринга не может занять всю ленту, мы можем вырезать неиспользуемую часть ленты (на каждый алгоритм разная часть)! Таким образом, необходимости в бесконечной ленте нет и всякий компьютер на 100% соответствует машине Тьюринга (и наоборот).
Наибольший парадокс, который я не могу разрешить, вот в чем: алгоритмы или формулы работают для произвольных чисел (a+b=c работает независимо от величин переменных, «а» может быть гуглплексом и т.д.). Машина Тьюринга как-бы тоже может работает с произвольными величинами. Компьютеры реализуют МТ, но размерность величин строго ограничена. Итак, каждую возможную программу можно заменить конечной памятью, где адрес — программа (вместе с входными данными), а значение по адресу — результат ее выполнения (как ни парадоксально, в схемотехнике так и сделано, просто логика сокращена!). Таким же образом мы можем заменить Машину Тьюринга гигантской конечной памятью, где адрес — алгоритм, а значение по адресу — результат выполнения алгоритма! Куда пропадает бесконечность???
1. Tzimie Автор
  30.03.2019 21:54
  #19963870
  И никакое выполнение алгоритма не может занять всю ленту.
  Если он не зациклился
  Выполняя программу на конечной машине вы не знаете, закрепилась программа или нет
  1. DjSapsan
    30.03.2019 22:04
    #19963888
    Это понятно. Но если занята вся память, значит машина зациклилась. Таким образом, после выполнения абсолютно любого алгоритма можно обрезать ленту.
    
    Hardcoin
    31.03.2019 14:56
    #19965406
    +1
    если занята вся память
    Этого не может произойти, лента бесконечная.
    
    Более того, если лента конечная и вся ячейки заняты, это не значит, что она зациклилась.
1. red75prim
  30.03.2019 22:42
  #19963956
  Таким же образом мы можем заменить Машину Тьюринга гигантской конечной памятью, где адрес — алгоритм, а значение по адресу — результат выполнения алгоритма!
  И как можно заменить алгоритм a+b конечной памятью? Если эта память конечна, то существуют максимальные значения a_m и b_m, для которых в памяти есть результат. Алгоритм может рассчитать (a_m + 1) + b_m, но в памяти этого значения не будет. Следовательно они не эквивалентны.
  1. DjSapsan
    30.03.2019 22:45
    #19963962
    Вот это я не могу понять. С одной стороны, Машина Тьюринга превосходит конечную память. С другой стороны, все возможные выполнимые алгоритмы конечны по памяти и по времени. Значит каждый возможный алгоритм можно воплотить в своей ячейке памяти.
    
    red75prim
    30.03.2019 23:05
    #19963996
    Что бы ни было записано в конечной памяти, алгоритм может рассчитать больше. Чтобы память была эквивалентна алгоритму, должно выполняться условие "если результат a+b находится в памяти, то и результаты (a+1) + b, a + (b+1), (a+1) + (b+1) находятся в памяти", а это условие выполняется только для актуально бесконечной памяти.
    
    DjSapsan
    30.03.2019 23:28
    #19964050
    Всё сложно )
    Очевидно, привести конкретный численный пример где алгоритм отличается от памяти принципиально невозможно. Ведь такой конкретный пример можно добавить в память. Парадокс?
    Я понимаю, что конкретный пример всегда конечен, а алгоритм безразмерен. Но есть одна тонкость. Допустим перечисляем все простые числа. Очевидно, что наивный алгоритм никогда не остановится. Поэтому каждый алгоритм, который остановится имеет, по крайней мере, счетчик, который в какой-то момент остановит его выполнение.
    Делаем вывод: ? алгоритм (? остановишийся алгоритм) можно записать в память.
    Не силен в кванторах, если сказать на естественном языке, то вот так: Каждый алгоритм из множества остановившихся алгоритмов можно записать в память.
    
    Cerberuser
    31.03.2019 06:48
    #19964480
    Загвоздка здесь вот в чём. Если считать этот счётчик частью алгоритма — т.е. если исключить из рассмотрения входные данные и считать, что машина Тьюринга всегда стартует на пустой ленте, — то да, любая программа, которая завершается, будет эквивалентна своему результату. А вот если считать, что на ленте может быть записано некоторое входное значение алгоритма (как и предполагается по определению) — у нас получится бесконечно большое количество результатов, каждый из которых может оказаться больше любой наперёд заданной памяти.
    
    DjSapsan
    31.03.2019 17:19
    #19965658
    Я примерно понял где я ошибся. Но всё не так просто. Я давно размышляю над вычислениями и даже работаю над идеей «действительного компьютера», где все вычисления выполняются над настоящими действительными числами.
    Если сократить, то вот мои размышления про МТ:
    Строго говоря, устройство управления (УУ) в Машине Тьюринга (МТ) это программа. А лента это только входные данные. Естественно, невозможно знать наперед входные данные, иначе мы знали бы будущее. Сама же программа (УУ) детерминирована и известна до конца (тут можно закинутся, что само УУ тоже может быть реализовано на отдельной МТ и так бесконечная рекурсия). Итак, хотя МТ является полностью абстрактной, ее логику мы реализовываем в физических «калькуляторах». Абсолютно строго придерживаясь соответствия, программа (УУ) в физических калькуляторах это сама программа плюс его железо (на самом деле, программа в RAM (или на перфоленте) это такой же физический объект как и процессор). А лента — это наши нажатия на кнопки. Из-за особенностей МТ часто считают, что на ленте записана программа, но это просто возможность МТ так делать (Тьюринг-полнота), а не само определение машины!
    Есть одна особенность, которая всё портит — мы не знаем, остановится ли МТ на некоторых входных данных. Это естественно и понятно, но всё равно ломает всю магию. Математически возможный выход — использовать такую МТ, которая каждое следующее действие выполняет в два раза быстрее предыдущего, что в математике делается на изи (но невозможно в реальности). Таким образом, каждый выполнимый алгоритм выполняется за конечное время. Гипотетически, так можно разделить МТ на два множества — остановившиеся и зациклившийся. Мой вопрос был в том, можно ли каждую МТ из множества остановившихся записать в конечную таблицу. Как видно, так нельзя, из-за бесконечной ленты.
    Я знаю, математический трюк ускорения можно оспорить. Но не суть. Проблема следующая — МТ абстрактна. Но математика не вычисляет саму себя. Всякое вычисление есть физический процесс. А все физические реализации — конечны. Так что любой компьютер можно заменить «пререндеренной» конечной таблицей с готовыми ответами.
    В процессе создания своего «действительного компьютера» я столкнулся с тяжелой проблемой — на него нельзя создать новый алгоритм. Все алгоритмы, которые на нем можно запустить должны быть уже до этого вычислены на обычной машине Тьюринга. Единственное, что я смог пока придумать — сложение и вычитание.
    Так вот я теперь сижу и думаю, что более абстрактно — Машина Тьюринга или «Действительный Компьютер»?
    Вообще, это тема для отдельной статьи
    
    Tzimie Автор
    31.03.2019 17:28
    #19965672
    Кстати, настоящую машину тьюринга можно построить в игре Жизнь
    
    DjSapsan
    31.03.2019 19:34
    #19965910
    Это я знаю и уже включил в свою черновую статью )
    
    Tzimie Автор
    31.03.2019 19:39
    #19965918
    Подписался. Буду читать)
    
    Tzimie Автор
    31.03.2019 20:01
    #19965952
    Вы там случайно не делаете машину Тьюринга в Майнкрафте?
    
    red75prim
    31.03.2019 19:59
    #19965946
    en.wikipedia.org/wiki/Real_computation
    
    DjSapsan
    31.03.2019 20:44
    #19966036
    «Blum–Shub–Smale machine» модель вычислений, которая работает с действительными числами. Меня смутило вот это: «BSS machines are more powerful than Turing machines (which in a sense are restricted to storing rational numbers only).»
    С мат. точки зрения всё идеально, но как воплотить такую машину в физическом виде? Я не нашел способа составления произвольных алгоритмов для «действительного компьютера». Всё что пока известно — вычисление «самого себя». С одной стороны, такой компьютер будет превосходить МТ по понятным причинам. Но с другой стороны, если на такой компьютер невозможно создать произвольный алгоритм, то толку от него будет мало.
    
    KvanTTT
    31.03.2019 23:50
    #19966446
    Сейчас я представляю "действительные вычисления" разве что как символьные, в которых число sqrt(2) представляется с помощью числа 2 и операции взятия корня. У таких вычислений проблемы со сколько нибудь нетривиальными задачами, в которых представления чисел будут расти до астрономических размеров. Например, как в системах компьютерной алгебры.
    
    С другой стороны, есть системы счисления с нецелым основанием, в которых некоторые действительные числа представляются нативно. Может на их основе тоже можно придумать что-нибудь интересное. Вообще самая оптимальная система счисления — с основанием e. Но оно нецелое, поэтому двоичная тоже является неплохим приближением (а троичная еще лучше).
    
    red75prim
    31.03.2019 09:30
    #19964622
    Ваши сомнения можно и проще выразить: "каждое натуральное число конечно, поэтому ничего бесконечного в натуральных числах (N) нет".
    
    Бесконечность появляется когда мы рассматриваем множество N как единое целое.
    
    Процедура добавления ещё одного натурального числа к имеющемуся конечному множеству — это не множество N. Это разве что часть определения, в котором не хватает: "Полученное множество будет равно N после добавления всех элементов множества N".
    
    Hardcoin
    31.03.2019 15:11
    #19965424
    все возможные выполнимые алгоритмы конечны по памяти и по времени
    Нет. Алгоритм a+b может занять больше любого заранее заданного количества памяти, если входные данные достаточно большие.
    
    Вашу гипотетическую таблицу "алгоритм -> результат" невозможно составить для натуральных чисел. Вам что бы записать все возможные входные данные, нужна бесконечная память.
1. Hardcoin
  31.03.2019 14:49
  #19965384
  Таким образом, необходимости в бесконечной ленте нет и всякий компьютер на 100% соответствует машине Тьюринга (и наоборот).
  Это утверждение не верно. Банальный бесконечный алгоритм "иди к следующему адресу памяти, повтори" на любой реальной машине упадет в исключение. На машине Тьюринга просто будет бесконечно выполняться. Это показывает, что нет, вы не можете заменить машину Тьюринга реальным компьютером и ожидать их 100% эквивалентность.
  
  Ответ на ваш вопрос — бесконечность пропадает тогда, когда вы выкидываете бесконечную ленту. Все алгоритмы, которые её используют, перестают работать.

Tzimie Автор
30.03.2019 22:18
#19963904
Нет, если алгоритм зациклился
А на конечной машине вы часто не можете узнать, зациклился он или нет

Что касается успешно остановившихся алгоритмов, то они используют всегда конечную память, но ее объем — алгоритмически неразрешимая проблема
1. DjSapsan
  30.03.2019 22:41
  #19963952
  Можно добавить правила для маркировки текущей ячейки
  
  используют всегда конечную память
  
  Значит все остановившиеся МТ можно заменить памятью с заранее написанным результатом, всего лишь элементарная комбинаторика.
  Что я хочу сказать? Даже в МТ нет бесконечности, единственное что она может сделать сверх этого — зациклится. Все алгоритмы работают с конечными величинами.
  1. Druu
    31.03.2019 10:06
    #19964688
    +1
    Даже в МТ нет бесконечности, единственное что она может сделать сверх этого — зациклится.
    Но вы не сможете никак отличить зациклившуюся от той, которой нужно "еще немного". Возьмите МТ, которая просто пишет на ленте единицы, до бесконечности. Вам придется постоянно "подклеивать" к этой МТ все новые и новые кусочки ленты, и этот процесс не закончится никогда. С-но никакой конечной ленты вам не хватит.
1. Druu
  31.03.2019 10:00
  #19964672
  А на конечной машине вы часто не можете узнать, зациклился он или нет
  Вообще не можете узнать, это же неразрешимая задача :)
  1. Tzimie Автор
    31.03.2019 10:13
    #19964698
    Я написал "часто"
    Потому что в общем случае это неразрешимая задача, но бывает что зацикленность очевидна
    
    Druu
    31.03.2019 10:19
    #19964704
    Я имел в виду не это, а то, что не важна конечность машины. Без разницы, конечная машина или не конечная — если у вас программа виснет "ациклически" (мозаику Пенроуза пусть рисует в какой-то кодировке, допустим), то, наблюдая ее поведение, вы никак и никогда не определите, что она висит, даже если у вас лента бесконечная.
    
    С конечной там обратная проблема — вы тогда будете обрубать все алгоритмы, которые требуют памяти больше, чем имеется.

slonpts
31.03.2019 00:07
#19964144
У меня возникло несколько вопросов, очевидных для математиков, но неочевидных, по крайней мере, для меня.

1.
коллекции вещественных создают любые фигуры

Я правильно понял, что можно использовать упорядоченную пару {тип, параметры типа} и записывать, например
{точка, {x, y}}
{треугольник, {точка1, точка2, точка3}}
{окружность, {точка_центра, радиус}}
{парабола, {директриса, точка_фокуса}}
?

2.
С помощью целых чисел мы можем создать вещественные
— как? Рациональные понятно — упорядоченная пара. Даже sqrt(5) понятно — {корень, {2, 5}}, вторая степень из 5.
А как с трансцендентными pi, e и др?

3. Что такое ТОЕ?
1. DjSapsan
  31.03.2019 00:19
  #19964170
  1) можно
  2) Вики
  3) Theory Of Everything
1. mayorovp
  31.03.2019 00:41
  #19964220
  А как с трансцендентными pi, e и др?
  Самый примитивный способ — школьный. Просто определяем действительное число как что-то, записанное в десятичной системе счисления. Более формально, действительное число — это пара из целого числа (называемого целой частью) и бесконечной последовательности цифр 0-9, ни один хвост которой не является последовательностью из одних только девяток.
  
  Чуть более продвинутое определение использует двоичную систему счисления как более простую.
  
  Другие определения более сложны, но зато не привязаны к конкретной форме записи.
  
  Третье определение: действительное число — это абсолютно сходящаяся последовательность рациональных чисел (но тут понадобится способ определения абсолютной сходимости на незамкнутых множествах).
  
  Четвертое: действительное число — это разрез множества рациональных чисел, т.е. такое разбиение Q на сумму A и B, что для любого x из A и y из B выполняется x<y.
  1. Druu
    31.03.2019 10:12
    #19964694
    Третье определение: действительное число — это абсолютно сходящаяся последовательность рациональных чисел (но тут понадобится способ определения абсолютной сходимости на незамкнутых множествах).
    Только не сама последовательность, а класс эквивалентности последовательностей с одинаковым пределом. Это существенный момент, т.к., выбирая другое отношение эквивалентности, мы получим другие числа.
    
    Sayonji
    31.03.2019 10:25
    #19964716
    Тогда уж не с одинаковым пределом, а с разностью стремящейся к нулю. Предела-то нет пока числа не построены.
1. 0xd34df00d
  31.03.2019 01:47
  #19964318
  C pi и e куда проще, кстати, чем с почти всеми вещественными числами: для их вычисления существует алгоритм (точнее, существует алгоритм, по рациональному ? дающий ?-приближение к ним), поэтому эти числа вообще можно отождествить с соответствующими алгоритмами.

maxzhurkin
31.03.2019 07:42
#19964510
Для обычной математики следующая мощность,
$p
o
w
e
r
s
e
t
(
?
c

)$ практически не нужна, обычно вся работа происходит со счетными множествами и множествами мощности континуума

так вот почему я не смог разобраться с помощью гуглёжки — туда не ступала нога обычного математика.

yurixi
31.03.2019 11:58
#19964978
Есть ли называния у чисел, количество цифр в которых не просто бесконечно, а несчётно?
1. Tzimie Автор
  31.03.2019 13:23
  #19965168
  Вас может заинтересовать так называемая длинная линия.
  
  https://en.m.wikipedia.org/wiki/Long_line_(topology)

Виды бесконечностей и вынос мозга +47

Известные факты

Малоизвестные факты

Гипотеза континуума — CH

Все выше и выше.

Сразу большой шаг

Недостижимые мощности

Еще дальше.

Иерархия больших мощностей.

Комментарии (151)

Tzimie Автор

Tzimie Автор

Tzimie Автор

Tzimie Автор

Tzimie Автор

Tzimie Автор

Tzimie Автор

Tzimie Автор

Tzimie Автор

Tzimie Автор

Tzimie Автор

Tzimie Автор

Tzimie Автор

Tzimie Автор

Tzimie Автор

Tzimie Автор

Tzimie Автор

Tzimie Автор

Tzimie Автор

Tzimie Автор

Tzimie Автор