В знаменитой задаче с монетами, которыми необходимо отсчитать сдачу, как известно, есть две беды.
— первая – это количество номиналов монет,
— вторая – это количество разрядов числа, представляющего сдачу.
И обе эти величины оказывают экспоненциальное воздействие на нагрузку машины Тьюринга, которая собственно и занимается подсчётом.
Признавать, что человек имеет сразу две зависимости, не принято даже в обществе алкоголиков. Поэтому я решил подстраховаться и избавиться от одной из этих проблем заранее. Путь это будет количество номиналов монет.

В двух словах суть проблемы описывается так: экспоненциальная зависимость. То есть выпуск нового типа монет несуществующего доселе номинала влечёт за собой увеличение количества комбинаций монет в два раза. Ещё один номинал – ещё в два раза, и так до условной бесконечности. При галопирующей инфляции, когда новые монеты/купюры выпускаются достаточно часто, для решения задачи придётся покупать более мощный компьютер. А где на это взять деньги при галопирующей то инфляции?

Итак, решение, которое на самом деле достаточно просто.
Если представить отрезок от нуля до С (сдача) с нанесёнными на ней точками, соответствующими номиналам монет, то любой интеллектуальный человек увидит примерно следующую картинку:

Ну, возможно в других цветах.
Итак, что мы можем сказать про красные точки? Конечно же то, что число, соответствующее любой этой точке, есть сумма, которую мы можем выдать в виде сдачи. Причём одной монетой. Возможно кто-то увидел что-то другое, но я, как художник, вкладывал именно этот смысл. И, как художник же, дорисую на этой картинке ещё одну точку, соответствующую сумме первой (слева направо) точки с этой же точкой (всё правильно: получится удвоенный номинал). Дорисую этим же цветом, ибо новая точка означает то же самое – эта сумма так же может быть сдачей.

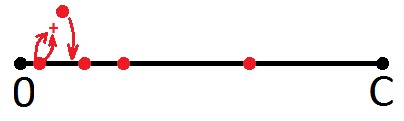
Далее беру первую точку и суммирую со второй, даже если вторая точка это предыдущая сумма (это неважно, ибо все точки здесь равны). Новую точку опять нанесу на отрезок.

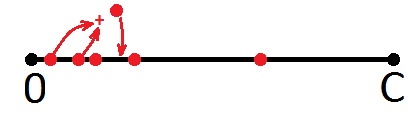
Если новая точка выходит за пределы отрезка, то ничего не рисуем, а возвращаемся к началу отрезка и берём следующую точку, то есть вторую. Далее то же самое (слева направо).
Собственно, когда точка С (напомню, это сдача) станет красной, можно считать, что решение найдено. А можно пройти полный цикл и найти оптимальное решение, что бы количество монет было минимальным.

С точки зрения программирования, здесь два цикла. Первый от 0 до С/2 (нет необходимости брать первую точку большей С/2, т.к. вторая точка всегда больше первой и в сумме они выйдут за границы отрезка). Второй цикл является встроенным в первый, он начинается с той же точки, на которую указывает внешний цикл и до момента, когда сумма покинет границы отрезка.
По сути это перебор: мы не теряем ни одного варианта, и гарантированно найдём оптимальное решение, или придём к выводу, что решения нет.

Давайте подсчитаем количество итерации внутри наших циклов. По внешнему циклу – это С/2, по внутреннему – где-то столько же. Умножим С/2 * С/2 = (С^2) / 4. Округлим до С в квадрате. Это наихудший вариант, когда весь наш отрезок просто состоит из красных точек. Если же между точками будут пробелы, количество итераций значительно уменьшится.
Как видим при определении сложности решения задачи мы не используем количество номиналов монет. Эта величина напрямую совсем никак не влияет на сложность решения. Влияют величины этих номиналов, скажем монета в 1 цент и сделает этот отрезок полностью красным. Поэтому эту монету лучше и не брать в расчёт, а в конце решения взять ближайшую к С красную точку и набросать сверху одноцентовиков. Но это уже момент оптимизации алгоритма, а она за рамками этой статьи.

Вот собственно и всё, что хотелось бы сказать. Рабочую версию программы можно найти здесь: github link

1. В файле init.h задать COINS_NUMBER — количество номиналов монет, и AMOUNT — сумма сдачи.
2. В файле coinc.c указать номиналы монет в массиве coins.
3. Под Linux запустить make_sh.
4. Запустить программу app на выполнение


Приведу какой-нибудь забавный пример. Представим, что в какой-нибудь стране к власти пришли математики и ввели в обращения 32 номинала монет: 2, 3, 5, 7, 11, 13, 17, 19… 131. Для удобства счёта выбрали только простые числа (ну не смешно ли?). И, что бы убедиться, что денежная реформа прошла успешно, послали в магазине гонца разменять купюру 5333 (тоже простое число). Кассир на стареньком одноядернике решил задачу: 39 монет номиналом 131 пифагороцентов, одну монету 127 и одну 97. Расчёт занял 3 секунды и чуть больше мегабайта памяти. Правительству доложили, что народ реформой доволен, считает быстро.


И пример, который чуточку сложнее проверить. Монеты, сто номиналов в такой вот странной последовательности: 0101, 0202, 0303… 9898, 9999, 100100. Сумма сдачи: 101010. Поиск решения занял 1 секунду и чуть больше мегабайта памяти. А решения, собственно, и нет, то есть нельзя такими монетами набрать такую сумму. С этими же монетами проверка суммы в 1 миллион займёт 26 мегабайт и сотни секунд, что говорит об экспоненциальной зависимости от суммы, но не количества номиналов монет.