28.01.2020 04:48
AlekDikarev 13 1800 Источник

Приветствую вас, глубокоуважаемые!


«… истинное место судна хотя и неизвестно, но оно не случайно, оно есть, но неизвестно в какой точке» Алексишин В. Г. и др. Практическое судовождение, 2006. стр. 71
«С двух краев галактики вышли пешеходы...» (С) Сергей Попов (Астрофизик)
В свете новых тенденций стиля арт-нуво я хотел написать о решении геодезических задач на плоской земле. Но пока еще заявление о том, что форма земли удобно аппроксимируется эллипсоидом не является ересью и крамолой, предлагаю всем интересующимся приобщиться к более консервативным моделям.

  • расстояние между двумя географическими точками
  • определение точки по известной, расстоянию до нее и азимутальному углу
  • определение положения точки по измеренным дальностям до известных точек (TOA, TOF)
  • определение положения точки по измеренным временам прихода сигнала (TDOA)

Все это на C#, Rust и Matlab, на сфере и эллипсоидах, с картинками, графиками, исходным кодом — под катом.

А это, релевантная КДПВ:



Для тех, кто спешит (я и сам такой), вот репозиторий на GitHub, где лежат все исходники с тестами и примерами.

Репозиторий организован очень просто: библиотека на данный момент представлена на трех языках и каждая реализация лежит в своей папке:


Наиболее полная реализация на C#: в отличие от остальных в ней присутствуют методы т.н. виртуальной длинной базы — это когда объект, положение которого необходимо определить неподвижен, и есть измеренные дальности до него из разных точек, с известным положением.

Чтобы посмотреть, как все работает, с какими параметрами вызывает и что возвращает, и провести разведку боем, есть разные демки и тесты:

  • Тестовое консольное приложение на C#
  • Тест всей библиотеки на Matlab
  • Демонстрационный скрипт по TOA/TDOA с красивыми картинками на Matlab
  • Скрипт на Matlab для сравнения точности решений геодезически задач на сфере (Haversine equations) и на эллипсоиде (Vincenty Equations)
  • Для реализации на Rust в коде библиотеки присутствуют тесты. И можно посмотреть как все работает просто запустив команду «Cargo -test»

Я постарался сделать библиотеку как можно более независимой и самодостаточной. Чтобы при желании можно было просто взять нужный кусок (сославшись на источник, конечно), не таская за собой все остальное.

Почти всегда углы — в радианах, расстояния в метрах, время в секундах.

Теперь, начнем, пожалуй, с начала:

Геодезические задачи


Есть две типовые геодезические задачи: прямая и обратная.

Если например, я знаю свои текущие координаты (широту и долготу), а потом прошагал 1000 километров строго на северо-восток, ну или на север. Какие теперь у меня будут координаты? — Узнать, какие у меня будут координаты — значит решить прямую геодезическую задачу.

То есть: Прямая геодезическая задача — это нахождение координат точки по известной, дистанции и дирекционному углу.

С обратной задачей все совсем понятно — например, я определил свои координаты, а потом прошагал сколько-то по прямой и снова определил свои координаты. Найти, сколько я прошел — значит решить обратную геодезическую задачу.

То есть: Обратная геодезическая задача — это нахождение расстояния между двумя точками с известными географическими координатами.

Решать эти задачи можно несколькими способами, в зависимости от необходимой точности и времени, которое вы готовы на это потратить.

Самый простой способ — представить что земля плоская — это сфера. Давайте попробуем.
Вот формула для решения прямой задачи (источник):

$\phi_2=arcsin(sin\phi_1cos\delta+cos\phi_1sin\delta cos\theta)$

$\lambda_2=\lambda_1+atan2(sin\theta sin\delta cos\phi_1, cos\delta-sin\phi_1sin\phi_2)$


Здесь $\phi_1$, $\lambda_1$ — широта и долгота исходной точки, $\theta$ — дирекционный угол, отсчитывающийся по часовой стрелке от направления на север (если смотреть сверху), $\delta$ — угловое расстояние d/R. d — измеренное (пройденное) расстояние, а R — радиус земли. $\phi_2$, $\lambda_2$ — широта и долгота искомой точки (ту, в которую мы пришли).

Для решения обратной задачи есть другая (не менее простая формула):

$a=sin^2(\Delta\phi/2)+cos\phi_1 cos\phi_2 sin^2(\Delta\lambda/2)$

$d=R * atan2(\sqrt a,\sqrt{1-a})$


Где $\phi_1$, $\lambda_1$ и $\phi_2$, $\lambda_2$ -координаты точек, R — земной радиус.

Описанные формулы называются Haversine Equations.

  • В реализации на C# соответствующие функции называются HaversineDirect и HaversineInverse и живут в Algorithms.cs.
  • В реализации на Rust это функции haversine_direct и haversine_inverse.
  • И наконец, на Matlab функции хранятся в отдельных файлах и вот обе функции:
    HaversineDirect и HaversineInverse

Для C# я буду приводить названия функций и ссылку на файл, где они находятся. Для Rust — только названия функций (коль скоро вся библиотека лежит в одном файле), а для Matlab — ссылку на соответствующий файл скрипта, потому что в Matlab одна функция — один скрипт.

Очевидно, что здесь есть какой-то подвох: земля не сфера, а плоскость и это как-то должно отражаться на применимости этих формул и/или на точности решения.

И действительно. Но для того, чтобы определиться с этим, нужно с чем-то сравнивать.
Еще в 1975 году Тадеуш Винценти (Thaddeus Vincenty) опубликовал вычислительно эффективное решение прямой и обратной геодезической задач на поверхности сфероида (известного более под ником Эллипсоид Революции, товарищ! Эллисоид Вращения), ставшее почти стандартом.

Описание устройства метода тянет на отдельную статью, поэтому я ограничусь лишь отсылкой на оригинальную работу Винценти и на онлайн-калькулятор с описанием алгоритма.

В библиотеке UCNLNav решение прямой и обратной геодезической задач по формулам Винценти лежит в следующих функциях:


Т.к. решение по Винценти итеративное, то в списке параметров присутствуют максимальное число итераций (it_limit), а в списке результатов — фактическое число итераций. Также присутствует порог, задающий условие остановки (epsilon). В большинстве случаев требуется не более 10 итераций, но для почти антиподных точек (как например северный и южный полюса) метод сходится плохо, и может потребоваться до 2000 итераций.

Самое важное отличие — данные формулы выполняют решение на сфероиде, и его параметры нужно передавать в функции. Для этого есть простая стуктура, которая его описывает.

Во всех реализациях можно в одну строчку получить один из стандартных эллипсоидов. (Сплошь и рядом применяется WGS84 [https://en.wikipedia.org/wiki/World_Geodetic_System] и его приведем в качестве примера):

  • На C#: В Algorithms.cs есть статическое поле Algorithms.WGS84Ellipsoid — его можно передавать в методы.
  • На Rust:
    let el: Ellipsoid = Ellipsoid::from_descriptor(&WGS84_ELLIPSOID_DESCRIPTOR);
  • На Matlab:
    el = Nav_build_standard_ellipsoid(‘WGS84’);

Наименование остальных параметров вполне очевидное и не должно вызвать неясностей.

Для того, чтобы понять, чего нам будет стоить применение решений для сферы вместо эллипса, реализации на Matlab присутствует скрипт.

В Matlab безумно удобно отображать всякое без лишних телодвижений, поэтому я выбрал его для демонстрации.

Логика его работы скрипта:

1. Берем точку с произвольными координатами

sp_lat_rad = degtorad(48.527683);
sp_lon_rad = degtorad(44.558815);

и произвольное направление (я выбрал примерно на запад):

fwd_az_rad = 1.5 * pi + (rand * pi / 4 - pi / 8);

2. Шагаем от нее на все увеличивающуюся дистанцию. Для чего сразу задаемся числом шагов и размером шага:

n_samples = 10000;
step_m = 1000; % meters
distances = (1:n_samples) .* step_m;

3. Для каждого шага решаем прямую геодезическую задачу на сфере и на эллипсоиде, получая искомую точку:


[ h_lats_rad(idx), h_lons_rad(idx) ] = Nav_haversine_direct(sp_lat_rad,...
            sp_lon_rad,...
            distances(idx),...
            fwd_az_rad,...
            el.mjsa_m);
        
[ v_lats_rad(idx), v_lons_rad(idx), v_rev_az_rad, v_its ] = Nav_vincenty_direct(sp_lat_rad,...
            sp_lon_rad,...
            fwd_az_rad,...
            distances(idx),...
            el,...
            VNC_DEF_EPSILON, VNC_DEF_IT_LIMIT);

4. Для каждого шага решаем обратные геодезические задачи — вычисляем расстояния между результатами, полученными на сфере и эллипсоиде:


[ v_dist(idx) a_az_rad, a_raz_rad, its, is_ok ] = Nav_vincenty_inverse(h_lats_rad(idx),...
            h_lons_rad(idx),...
            v_lats_rad(idx),...
            v_lons_rad(idx),...
            el,...
            VNC_DEF_EPSILON, VNC_DEF_IT_LIMIT);

5. Проверяем прямые решения обратными для обоих методов:


[ ip_v_dist(idx) a_az_rad, a_raz_rad, its, is_ok ] = Nav_vincenty_inverse(sp_lat_rad,...
            sp_lon_rad,...
            v_lats_rad(idx),...
            v_lons_rad(idx),...
            el,...
            VNC_DEF_EPSILON, VNC_DEF_IT_LIMIT);
        
ip_h_dist(idx) = Nav_haversine_inverse(sp_lat_rad,...
            sp_lon_rad,...
            v_lats_rad(idx),...
            v_lons_rad(idx),...
            el.mjsa_m);

В скрипте эта последовательность выполняется сначала для шага = 1000 м, а потом для шага = 1 метр.

Сначала посмотрим, насколько отличаются результаты прямых решений по координатам (широте и долготе), для чего вычислим векторы «дельт», благо на Matlab все пишется в одну строчку:


d_lat_deg = radtodeg(v_lats_rad - h_lats_rad); % дельты по широте (в градусах)
d_lon_deg = radtodeg(v_lons_rad - h_lons_rad); % дельты по долготе (в градусах)

По оси абцисс будем отображать в логарифмическом масштабе, т.к. у нас расстояния меняются от 1 до 10000 км:

figure
semilogx(distances, d_lat_deg, 'r');
title('Direct geodetic problem: Vincenty vs. Haversine (Latitude difference)');
xlabel('Distance, m');
ylabel('Difference, °');

figure
semilogx(distances, d_lon_deg, 'r');
title('Direct geodetic problem: Vincenty vs. Haversine (Longitude difference)');
xlabel('Distance, m');
ylabel('Difference, °');

В результате получаем такие графики для широты:



И для долготы:



Я плохо понимаю в градусах, всегда руководствуюсь методом для прикидки «на глазок»:
1° чего-нибудь это в среднем 100-110 км. И если ошибка больше миллионной или хотя бы стотысячной части градуса — это плохие новости.

Дальше посмотрим расстояния между исходной точкой и точкой, получаемой на каждом шаге по формулам для сферы и эллипсоида. Расстояние вычислим по формулам Винценти (как заведомо более точным — автор обещает ошибку в миллиметрах). Графики в метрах и километрах это гораздо более осязаемо и привычно:

figure
semilogx(distances, v_dist, 'r');
title('Direct geodetic problem: Vincenty vs. Haversine (Endpoint difference by Vincenty)');
xlabel('Distance, m');
ylabel('Difference, m');

В результате получаем такую картину:



Получается, что на дальностях 10000 км методы расходятся на 10 км.

Если теперь все повторить для шага в 1000 раз меньше, т.е. когда весь диапазон по оси Х будет не 10000 км а всего 10 км, то картина выходит следующая:



То есть, на дальности 10 км набегает всего 20 метров, а на 1-2 метра формулы расходятся только на дистанциях порядка 1000 метров.

Вывод капитана очевидность: если для задачи точность формул с решением на сфере достаточна, то используем их — они проще и быстрее.

Ну, а для тех, кому миллиметровой точности недостаточно, в 2013 году была опубликована работа с описанием решения геодезических задач с нанометровой (!) точностью. Не уверен, что могу сходу придумать, где такое может понадобится — разве что при геодезических изысканиях при постройке гравитационно-волновых детекторов или чего-то совершенно фантастического ).

Теперь перейдем к самому вкусному:

Решение навигационных задач


На данный момент библиотека умеет определять:

  • Местоположение объекта по дальностям до точек, с известными координатами в 2D и 3D. Такое мы называет TOA — Time Of Arrival (или что более правильно TOF — Time Of Flight)
  • Местоположение объекта по разностям времен прихода в 2D и 3D. Такое мы называем TDOA (Time Difference Of Arrival).

В реальности мы всегда измеряем дальности или времена прихода сигнала (а соответственно, и их разности) с ошибками, с шумом. Поэтому решение навигационных задач в подавляющем числе случаев — это минимизация ошибки. Метод наименьших квадратов и вот это вот все.

То, что нужно минимизировать, называется функцией невязки.

Для задач TOA она выглядит так:

$argmin\epsilon(x,y,z)=\sum_{i=1}^{N}[\sqrt{(x-x_i)^2+(y-y_i)^2+(z-z_i)^2)}-r_i]^2$


Где $\epsilon(x,y,z)$ — значение функции невязки для некоей точки с координатами $(x,y,z)$; N — число опорных точек, имеющих координаты $(x_i,y_i,z_i)$, $r_i$ — измеренные расстояния от опорных точек до позиционируемого объекта.

А для задач TDOA вот так:

$argmin\epsilon(x,y,z)=\sum_{i=1,j=2,i\neq j}^{N}[\sqrt{(x-x_i)^2+(y-y_i)^2+(z-z_i)^2)}- \\ \sqrt{(x-x_j)^2+(y-y_j)^2+(z-z_j)^2)}-\nu(t_{Ai}-t_{Aj})]^2 $



Здесь все тоже самое, только рассматриваются разные пары опорных точек и соответствующие времена прихода $t_{Ai}$ и $t_{Aj}$, а $\nu$ — скорость распространения сигнала.

А вот так эти функции выглядят в коде:

На C#:
/// <summary>
/// TOA problem residual function
/// </summary>
/// <param name="basePoints">base points with known locations and distances to them</param>
/// <param name="x">current x coordinate</param>
/// <param name="y">current y coordinate</param>
/// <param name="z">current z coordinate</param>
/// <returns>value of residual function in specified location</returns>
public static double Eps_TOA3D(TOABasePoint[] basePoints, double x, double y, double z)
{
     double result = 0;
     double eps = 0;
     for (int i = 0; i < basePoints.Length; i++)
    {
         eps =  Math.Sqrt((basePoints[i].X - x) * (basePoints[i].X - x) +
                                 (basePoints[i].Y - y) * (basePoints[i].Y - y) +
                                 (basePoints[i].Z - z) * (basePoints[i].Z - z)) - basePoints[i].D;
         result += eps * eps;
    }
    return result;
}

/// <summary>
/// TDOA problem residual function
/// </summary>
/// <param name="baseLines">base lines, each represented by two base points with known locations and times of arrival</param>
/// <param name="x">current x coordinate</param>
/// <param name="y">current y coordinate</param>
/// <param name="z">current z coordinate</param>
/// <returns>value of residual function in specified location</returns>
public static double Eps_TDOA3D(TDOABaseline[] baseLines, double x, double y, double z)
{
     double result = 0;
     double eps;
     for (int i = 0; i < baseLines.Length; i++)
     {
          eps = Math.Sqrt((baseLines[i].X1 - x) * (baseLines[i].X1 - x) +
                                 (baseLines[i].Y1 - y) * (baseLines[i].Y1 - y) +
                                 (baseLines[i].Z1 - z) * (baseLines[i].Z1 - z)) -
                   Math.Sqrt((baseLines[i].X2 - x) * (baseLines[i].X2 - x) +
                                 (baseLines[i].Y2 - y) * (baseLines[i].Y2 - y) +
                                 (baseLines[i].Z2 - z) * (baseLines[i].Z2 - z)) - baseLines[i].PRD;
          result += eps * eps;
      }
      return result;
}


На Rust:

pub fn eps_toa3d(base_points: &Vec<(f64, f64, f64, f64)>, x: f64, y: f64, z: f64) -> f64 {
    
    let mut result: f64 = 0.0;
    
    for base_point in base_points {
        result += (((base_point.0 - x).powi(2) +
                    (base_point.1 - y).powi(2) +
                    (base_point.2 - z).powi(2)).sqrt() - base_point.3).powi(2);
    }

    result
}
 
pub fn eps_tdoa3d(base_lines: &Vec<(f64, f64, f64, f64, f64, f64, f64)>, x: f64, y: f64, z: f64) -> f64 {

    let mut result: f64 = 0.0;
    
    for base_line in base_lines {
        result += (((base_line.0 - x).powi(2) +
                    (base_line.1 - y).powi(2) +
                    (base_line.2 - z).powi(2)).sqrt() -                  
                   ((base_line.3 - x).powi(2) +
                    (base_line.4 - y).powi(2) +
                    (base_line.5 - z).powi(2)).sqrt() - base_line.6).powi(2);        
    }

    result
}


На Matlab:

% base_points(n, c)
% n - a base point index
% c = 1 -> x
% c = 2 -> y
% c = 3 -> z
% c = 4 -> estimated distance

function [ result ] = Nav_eps_toa3d(base_points, x, y, z)
result = 0.0;
for n = 1:length(base_points)
    result = result + (sqrt((base_points(n, 1) - x)^2 +...
                            (base_points(n, 2) - y)^2 +...
                            (base_points(n, 3) - z)^2) - base_points(n, 4))^2;
end

function [ result ] = Nav_eps_tdoa3d(base_lines, x, y, z)
result = 0.0;
for n = 1:length(base_lines)
   result = result + (sqrt((base_lines(n, 1) - x)^2 +...
                           (base_lines(n, 2) - y)^2 +...
                           (base_lines(n, 3) - z)^2) -...
                      sqrt((base_lines(n, 4) - x)^2 +...
                           (base_lines(n, 5) - y)^2 +...
                           (base_lines(n, 6) - z)^2) -...
                      base_lines(n, 7))^2;
end


Как можно видеть, обе функции работают с переменным числом опорных точек или линий. Вообще задачи могут быть разные, и функции невязки тоже.

Например, можно решать задачу не только определения местоположения, но и определения ориентации. В этом случае функция невязки будет содержать один или несколько углов.

Остановимся чуть более подробно на внутреннем устройстве библиотеки


На данном этапе библиотека работает с 2D и 3D задачами и сам решатель не знает и не хочет знать как выглядит минимизируемый функционал. Это достигается следующим способом.

У решателя есть две ипостаси: 2D и 3D решатели, основанные на методе Нелдера-Мида или, как еще его называют, метода Симплекса.

Так как этому методу не требуется вычисление производных (т.н. derivative-free minimization), то в идеале пользователь библиотеки может применять свои собственные функции невязки если такое потребуется. Плюс, теоретически нет никакого верхнего ограничения на количество опорных точек, используемых при решении задачи.

В C# и Rust 2D и 3D Решатели — Generic-методы:

public static void NLM2D_Solve<T>(Func<T[], double, double, double, double> eps, 
   T[] baseElements,...

// пример вызова функции невязки в теле решателя:
fxi[0] = eps(baseElements, xix[0], xiy[0], z);

Пример вызова самого решателя:

public static void TOA_NLM2D_Solve(TOABasePoint[] basePoints,
                                           double xPrev, double yPrev, double z,
                                           int maxIterations, double precisionThreshold, double simplexSize,
                                           out double xBest, out double yBest, out double radialError, out int itCnt)
{
     NLM2D_Solve<TOABasePoint>(Eps_TOA3D,
                               basePoints, xPrev, yPrev, z,
                               maxIterations, precisionThreshold, simplexSize,
                               out xBest, out yBest, out radialError, out itCnt);
}

На Rust…


pub fn nlm_2d_solve<T>(eps: Eps3dFunc<T>, base_elements: &Vec<T>...

Все идентично, с точностью до синтаксиса языка.

В Matlabe же, с присущим ему волюнтаризмом, сам решатель понятия не имеет что за базовые элементы ему передаются — пользователь сам должен позаботиться, чтобы передаваемые в решатель ссылка на функцию невязки и набор опорных элементов были совместимы:


function [ x_best, y_best, rerr, it_cnt ] = Nav_nlm_2d_solve(eps, base_elements, ....

И соответственно, вызов решателя выглядит так:


function [ x_best, y_best, rerr, it_cnt ] = Nav_toa_nlm_2d_solve(base_points, x_prev, y_prev, z,...
    max_iterations, precision_threshold, simplex_size)
    [ x_best, y_best, rerr, it_cnt ] = Nav_nlm_2d_solve(@Nav_eps_toa3d, base_points, x_prev, y_prev, z,...
        max_iterations, precision_threshold, simplex_size);
end

Для демонстрации решения TOA и TDOA задач есть специальный скрипт на Matlab.

Демонстрация в 2D выбрана не случайно — я не уверен что могу придумать, как просто и информативно отобразить трехмерную функцию невязки =)

Итак. В начале скрипта есть параметры, которые можно менять:


%% parameters
n_base_points = 4;              % число опорных точек 
area_width_m = 1000;         % размер области
max_depth_m = 100;           % максимальная глубина (координата Z)
propagation_velocity = 1500;% для меня привычная область - гидроакустика

max_iterations = 2000;         % максимальное число итераций 
precision_threshold = 1E-9;   % порог точности
simplex_size = 1;                 % стартовый размер симплекса в метрах

contour_levels = 32;             % число линий уровня для отображения

range_measurements_error = 0.01; % 0.01 means 1% of corresponding slant range 
                                                   % амлитуда случайной ошибки - оптимистично примем 1%

Положение искомой точки задается случайным образом в указанной области:


%% actual target location
r_ = rand * area_width_m / 2;
az_ = rand * 2 * pi;
actual_target_x = r_ * cos(az_);
actual_target_y = r_ * sin(az_);
actual_target_z = rand * max_depth_m;

Далее, случайно располагаем опорные точки, вычисляем дистанцию от искомой до них и отображаем все:


%% base points
figure
hold on
grid on

base_points = zeros(n_base_points, 4);

for n = 1:n_base_points
   r_ = area_width_m / 2 - rand * area_width_m / 4;
   az_ = (n - 1) * 2 * pi / n_base_points;
   base_x = r_ * cos(az_);
   base_y = r_ * sin(az_);
   base_z = rand * max_depth_m;
   dist_to_target = Nav_dist_3d(base_x, base_y, base_z, actual_target_x, actual_target_y, actual_target_z);
   base_points(n, :) = [ base_x base_y base_z dist_to_target ];   
end

N =1:n_base_points;
plot3(actual_target_x, actual_target_y, actual_target_z,...
    'p',...
    'MarkerFaceColor', 'red',...
    'MarkerEdgeColor', 'blue',...
    'MarkerSize', 15);

plot3(base_points(N, 1), base_points(N, 2), base_points(N, 3),...
    'o',...
    'MarkerFaceColor', 'green',...
    'MarkerEdgeColor', 'blue',...
    'MarkerSize', 15);

for n = 1:n_base_points
   line([ actual_target_x, base_points(n, 1) ], [ actual_target_y, base_points(n, 2) ], [ actual_target_z, base_points(n, 3) ]); 
end

view(45, 15);
legend('target', 'base points');
title('Placement of base stations and the target');
xlabel('X coordinate, m');
ylabel('Y coordinate, m');
zlabel('Z coordinate, m');

В итоге получаем такую картинку:



Добавляем к измерениям дистанций случайные ошибки:


% adding range measurement errors
base_points(N, 4) = base_points(N, 4) + base_points(N, 4) *...
    (rand * range_measurements_error - range_measurements_error / 2);

Строим функцию невязки для выбранной области с некоей децимацией — иначе расчеты могут занять ощутимое время. Я выбрал размер области 1000 х 1000 метров и считаю функцию невязки по всей области через 10 метров:


% error surface tiles
tile_size_m = 10;
n_tiles = area_width_m / tile_size_m;

%% TOA solution
error_surface_toa = zeros(n_tiles, n_tiles);
for t_x = 1:n_tiles
   for t_y = 1:n_tiles      
      error_surface_toa(t_x, t_y) = Nav_eps_toa3d(base_points,...
          t_x * tile_size_m - area_width_m / 2,...
          t_y * tile_size_m - area_width_m / 2,...
          actual_target_z);
   end
end

figure
surf_a = [1:n_tiles] * tile_size_m - area_width_m / 2;
surf(surf_a, surf_a, error_surface_toa);
title('TOA solution: Residual function');
xlabel('X coordinate, m');
ylabel('Y coordinate, m');
view(45, 15);

Вот так выглядит функция невязки:



Я конечно немного слукавил — взаимные расположения опорных точек и искомой выбираются так, что они всегда образуют выпуклую фигуру с искомой точкой внутри. Во многом благодаря этому поверхность имеет один минимум, который находится без особых проблем.

Въедливый читатель может изменить этот порядок вещей и попробовать расставить опорные точки и искомую совершенно случайно.

Теперь отобразим все вместе. На поверхности это сделать сложно — разные величины по вертикальной оси. Поэтому удобно все нарисовать на двумерном срезе:


figure
hold on
contourf(surf_a, surf_a, error_surface_toa, contour_levels);
plot(actual_target_x, actual_target_y,...
    'p',...
    'MarkerFaceColor', 'red',...
    'MarkerEdgeColor', 'blue',...
    'MarkerSize', 15);

plot(base_points(N, 1), base_points(N, 2),...
    'o',...
    'MarkerFaceColor', 'green',...
    'MarkerEdgeColor', 'blue',...
    'MarkerSize', 15);

[ x_prev, y_prev ] = Nav_toa_circles_1d_solve(base_points, actual_target_z, pi / 180, 10, 0.1); 
[ x_best, y_best, rerr, it_cnt ] = Nav_toa_nlm_2d_solve(base_points, x_prev, y_prev, actual_target_z,...
    max_iterations, precision_threshold, simplex_size);

plot(x_best, y_best,...
    'd',...
    'MarkerFaceColor', 'yellow',...
    'MarkerEdgeColor', 'blue',...
    'MarkerSize', 7);

title(sprintf('TOA Solution: Residual function. Target location estimated with E_{radial} = %.3f m in %d iterations', rerr, it_cnt));
xlabel('X coordinate, m');
ylabel('Y coordinate, m');
legend('Residual function value', 'Actual target location', 'Base points', 'Estimated target location');

В результате получается примерно так:



В заголовке графика отображается радиальная ошибка — корень из финального значения функции невязки. На графике видно, что реальное местоположение и вычисленное хорошо совпадают, но масштаб не позволяет определить насколько хорошо.

Поэтому отобразим вычисленное местоположение искомой точки и реальное ее местоположение отдельно и посчитаем расстояние между ними:


figure
hold on
grid on

dx = actual_target_x - x_best;
dy = actual_target_y - y_best;

plot(0, 0,...
    'p',...
    'MarkerFaceColor', 'red',...
    'MarkerEdgeColor', 'blue',...
    'MarkerSize', 15);

plot(dx, dy,...
    'd',...
    'MarkerFaceColor', 'yellow',...
    'MarkerEdgeColor', 'blue',...
    'MarkerSize', 7);

plot(-dx * 2, -dy * 2, '.w');
plot(dx * 2, dy * 2, '.w');

d_delta = Nav_dist_3d(actual_target_x, actual_target_y, actual_target_z, x_best, y_best, actual_target_z);
title(sprintf('TOA Solution: Actual vs. Estimated location, distance: %.3f m', d_delta));
xlabel('X coordinate, m');
ylabel('Y coordinate, m');
legend('Actual target location', 'Estimated target location');

Вот как это выглядит:



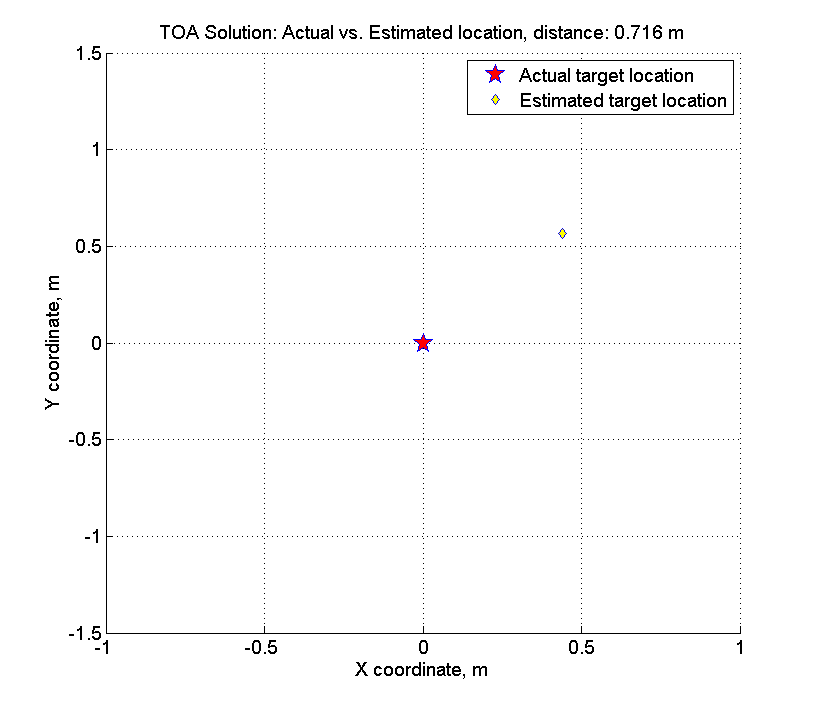
Вспомним, что у нас амплитуда случайной ошибки — 1% от дальности, в среднем дальность ~200-400 метров, т.е. амплитуда ошибки составляет порядка 2-4 метров. При поиске решения мы ошиблись всего на 70 сантиметров.

Теперь по аналогии попробуем решить задачу TDOA на тех же данных. Для этого притворимся, что нам известны только времена прихода сигналов с искомой точки на опорные (или наоборот — не принципиально) — просто разделим наши дистанции на скорость распространения сигнала — важны лишь их разности а не абсолютные величины.


% since TDOA works with time difference of arriaval,
% we must recalculate base point's distances to times
base_points(N,4) = base_points(N,4) / propagation_velocity;
base_lines = Nav_build_base_lines(base_points, propagation_velocity);

Строим и рисуем поверхность ошибок:


error_surface_tdoa = zeros(n_tiles, n_tiles);
for t_x = 1:n_tiles
   for t_y = 1:n_tiles      
      error_surface_tdoa(t_x, t_y) = Nav_eps_tdoa3d(base_lines,...
          t_x * tile_size_m - area_width_m / 2,...
          t_y * tile_size_m - area_width_m / 2,...
          actual_target_z);
   end
end

figure
surf(surf_a, surf_a, error_surface_tdoa);
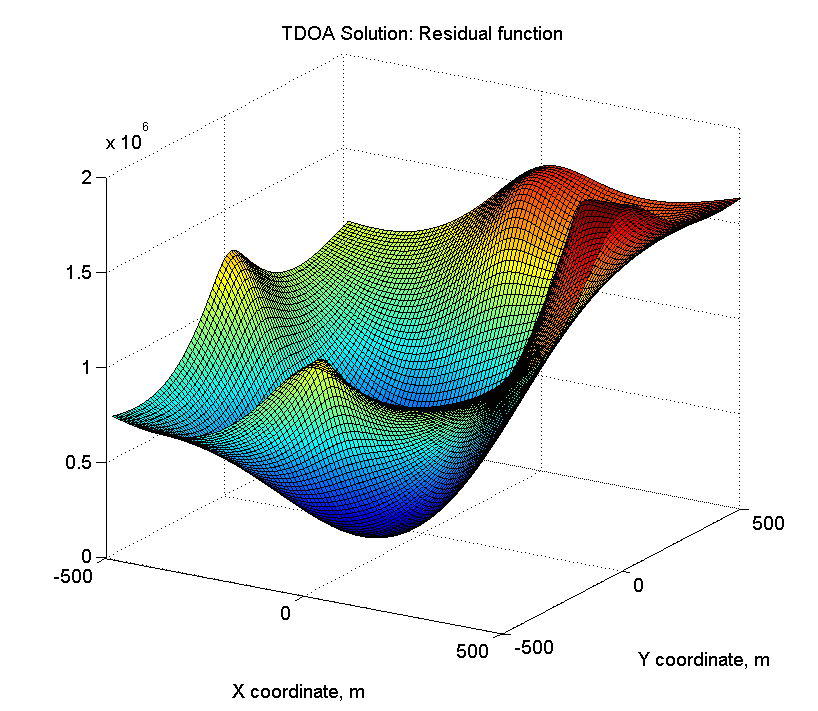
title('TDOA Solution: Residual function');
xlabel('X coordinate, m');
ylabel('Y coordinate, m');
view(45, 15);

Получается что-то такое:



И вид «сверху» с опорными точками, реальным и вычисленным положениями искомой точки:



И более детально, расхождение реального и вычисленного местоположения:



В этом конкретном случае решение по TDOA оказалось даже лучше, чем по TOA — абсолютная ошибка составляет 0.3 метра.

Хорошо в модели — всегда точно знаешь, где фактически расположена искомая точка. На воздухе хуже — может быть несколько точек зрения, под водой ты просто что-то вычислил и все — в 99% случаев, чтобы вычислить отклонение от фактического местоположения, его (это местоположение) тоже сначала надо вычислить.

Теперь, в качестве заключения, объединим наши новые знания про геодезические и навигационные задачи.

Финальный аккорд


Максимально приблизим ситуацию к реальной жизни:

  • пусть у нас опорные точки имеют встроенные GNSS-приемники и мы знаем только их географические координаты
  • вертикальная координата нам неизвестна (3D Задача)
  • мы измеряем только времена прихода сигнала от опорных точек на искомой или наоборот

Такая ситуация описана в самом последнем тесте во всех трех реализациях. Я как-то обделил Rust, и финальный пример разберу на нем.

Итак, самый последний тест в библиотеке. В качестве координат искомой точки я выбрал место в парке, где часто гуляю с собакой.


#[test]
fn test_tdoa_locate_3d() {
   let el: Ellipsoid = Ellipsoid::from_descriptor(&WGS84_ELLIPSOID_DESCRIPTOR);

   let base_number = 4; // 4 опорные точки
   let start_base_z_m: f64 = 1.5; // координата Z первой из опорных точек
   let base_z_step_m = 5.0; // у каждой следующей она будет увеличиваться на 5 метров

   let actual_target_lat_deg: f64 = 48.513724 // singed degrees
   let actual_target_lon_deg: f64 = 44.553248; // signed degrees
   let actual_target_z_m: f64 = 25.0;          // meters - внезапно, не на поверхности земли!

   // generate base points via Vincenty equations
   let mut base_points = Vec::new();

   let start_dst_projection_m = 500.0;          // первая базовая точка на расстоянии 500 метров
   let dst_inc_step_m = 50.0;                      // каждая последующая - на 50 метров дальше
                      
   // azimuth step
   let azimuth_step_rad = PI2 / base_number as f64; // опорные точки вокруг искомой

   let actual_target_lat_rad = actual_target_lat_deg.to_radians();
   let actual_target_lon_rad = actual_target_lon_deg.to_radians();

   // signal propagation speed
   let velocity_mps = 1450.0; // m/s, я привык к скорости звука в воде 
   // генерируем положения опорных точек
   for base_idx in 0..base_number {
       // текущая проекция наклонной дальности на поверхность земли
       let dst_projection_m = start_dst_projection_m + dst_inc_step_m * base_idx as f64;
       // азимутальный угол на текущую опорную точку
       let azimuth_rad = azimuth_step_rad * base_idx as f64;
       // вычисляем координаты текущей опорной точки по формулам Vincenty
       let vd_result = vincenty_direct(actual_target_lat_rad, actual_target_lon_rad, 
           azimuth_rad, dst_projection_m, 
           &el, 
           VNC_DEF_EPSILON, VNC_DEF_IT_LIMIT);
                
       // приращиваем координату Z
       let base_z_m = start_base_z_m + base_z_step_m * base_idx as f64;
       // разность вертикальных координат для определения наклонной дальности
       let dz_m = actual_target_z_m - base_z_m;
       // наклонная дальность по теореме Пифагора
       let slant_range_m = (dst_projection_m * dst_projection_m + dz_m * dz_m).sqrt();
       
       // добавляем опорную точку. И превращаем дальность во время поделив на скорость звука      Rust приятно радует удобством!
       base_points.push((vd_result.0.to_degrees(), vd_result.1.to_degrees(), base_z_m, slant_range_m / velocity_mps));
   }
        
    // если первое приближение неизвестно - все приравниваем NAN-ам
    let lat_prev_deg = f64::NAN;
    let lon_prev_deg = f64::NAN;
    let prev_z_m = f64::NAN;

    // запускаем решение
    let tdoa_3d_result = tdoa_locate_3d(&base_points,
    lat_prev_deg, lon_prev_deg, prev_z_m,
       NLM_DEF_IT_LIMIT, NLM_DEF_PREC_THRLD, 10.0, &el, velocity_mps);

    // вычисляем расстояние от реального положения искомой точки до вычисленного
    let vi_result = vincenty_inverse(actual_target_lat_rad, actual_target_lon_rad, 
       tdoa_3d_result.0.to_radians(), tdoa_3d_result.1.to_radians(),
       &el, VNC_DEF_EPSILON, VNC_DEF_IT_LIMIT);        

    assert!(vi_result.0 < start_dst_projection_m * 0.01, "Estimated location is farer than limit (1%): {}", vi_result.0);
    assert_approx_eq!(tdoa_3d_result.2, actual_target_z_m, start_dst_projection_m * 0.05);
        
    assert!(tdoa_3d_result.3 < start_dst_projection_m * 0.01, "Residual function greater than limit (1%): {}", tdoa_3d_result.3);
    assert!(tdoa_3d_result.4 < NLM_DEF_IT_LIMIT, "Method did not converge: iterations limit exeeded {}", tdoa_3d_result.4);
}

В результате имеем:
Реальное местоположение (Lat, Lon, Z): 48.513724 44.553248 25
Вычисленное положение (Lat, Lon, Z): 48.513726 44.553252 45.6
Расстояние между точками по поверхности (м): 0.389
Разность по координате Z (м): 20.6

Совпадение «в плане» — очень хорошее, ошибка составляет всего 40 сантиметров, а по вертикальной координате — 20 метров. Почему так происходит предлагаю подумать читателям =)

P.S.


Описываемая библиотека — чисто образовательный проект, который я планирую развивать и пополнять дальше. В планах реализация на C и написание всеобъемлющей документации.

На этом разрешите откланяться, спасибо за внимание. Буду бесконечно рад любому feedback.
Надеюсь, статья и библиотека будут полезны.
Про любые ошибки (грамматические и логические) сообщайте — я исправлю.

P.P.S


На всякий случай приведу здесь ссылку на онлайн (и не только) интерпретаторы Matlab/Octave, которыми пользуюсь сам: