В 2017 двое ученых, канадец John Aycock и британка Tara Copplestone, опубликовали анализ классической игры Entombed для игровой приставки Atari 2600. Механика этой игры, выпущенной в 1982, крайне проста: археолог, управляемый игроком, должен пробраться по прокручивающимся снизу вверх катакомбам, уворачиваясь от зомби.

У Atari 2600 было всего 128 байт ОЗУ; тем не менее, кажущийся бесконечным лабиринт при каждом запуске был новым, т.е. генерировался в памяти. Как же программистам это удалось? Вот комментарий Стивена Сидли — программиста, 38 лет назад создавшего эту игру:

Основную часть генератора лабиринтов написал какой-то уволившийся торчок. Я связался с ним, чтобы выяснить, как его алгоритм работал. Он ответил, что придумал этот алгоритм, когда был вусмерть накурен и вдобавок пьян, что написал его сразу на ассемблере прежде чем вырубился, а потом даже близко не мог вспомнить, в чем его алгоритм состоял.

Генераторы лабиринтов

В Википедии перечислены дюжина разных алгоритмов для генерации лабиринтов. Наибольший интерес для игровых приставок представляет «алгоритм Эллера», созданный в том же 1982 Мартином Эллером из Microsoft. Алгоритм Эллера позволяет построчно создавать связные лабиринты без циклов, причем для генерации лабиринта неограниченной высоты достаточно хранить в памяти только пару последних строк. Казалось бы, это как раз то, что нужно для Entombed! Но увы, с игровой механикой вертикального скроллера алгоритм Эллера несовместим, потому что в получившемся лабиринте регулярно приходится обходить препятствия сверху. Для демонстрации этого я слегка модифицировал алгоритм Эллера, чтобы лабиринт создавался в матрице из «стен» и «проходов», как и в Entombed:



Более изощренные алгоритмы, использующие рекурсию и т.п., не уложились бы в 128 байт ОЗУ. Итак, требования к алгоритму для Entombed такие:

1. Построчная генерация лабиринтов неограниченной высоты;
2. В создаваемых лабиринтах должно быть как можно меньше несвязных участков; (у игрока есть ограниченная возможность «пробивать стены», так что редкие несвязности не представляет проблемы)
3. Создаваемые лабиринты должны состоять в основном из ветвящихся и соединяющихся вертикальных проходов — так, чтобы для прохождения лабиринта не требовалось движение вверх;
4. Для генерации новых строк лабиринта должны использоваться только несколько последних сгенерированных строк. (Поскольку у Atari 2600 нет видеобуфера, то все видимые на экране строки лабиринта должны в каком-то виде храниться в 128 байтах основной памяти).

Кто и как создал этот алгоритм?

Двое ученых, называющих себя «археологами видеоигр», решили начать свои изыскания именно с Entombed — игры про археолога в лабиринте. В ходе своего исследования они разыскали Стивена Сидли, и спросили его, какой алгоритм он использовал для генерации лабиринта. Как уже было упомянуто, Сидли им ответил, что даже автор алгоритма не мог вспомнить, в чем его алгоритм состоял, а сам Сидли — тем более. Затем исследователи попытались найти «торчка», создавшего этот алгоритм; вторая половина истории нашлась в интервью, опубликованном в 2008:

Генератор лабиринтов для Entombed создали Дункан [Duncan Muirhead] и я [Paul Allen Newell]. Как-то вечером после работы мы с Дунканом пошли выпить, и у нас завязалось обсуждение того, возможно ли генерировать бесконечный лабиринт, в котором всегда есть проход. Тогда мы не думали о создании игры, нас интересовала сама задача генерации лабиринта. Алгоритм мы придумали вместе, и поскольку я умел программировать для VCS [Atari 2600], то за выходные я создал работоспособный прототип. Нас обоих впечатлило, насколько реализация получилась элегантной. Потом мы показали этот прототип начальству, и они решили, что из него получится отличная игра. Мне это уже не было интересно, так что я доделал Towering Inferno, задействовав там часть нашего алгоритма, и уволился. После моего ухода фирма наняла Стивена Сидли, и передала генератор лабиринтов ему. Существенную часть моего кода ему пришлось удалить, чтобы освободить место для игровой механики. [У Atari 2600, кроме жестких ограничений по объемам ОЗУ и ПЗУ, было еще и требование, чтобы генерация каждой строки пикселей занимала ровно 76 тактов примечание автора].

Сидли упомянул, что код генератора лабиринтов был написан на ассемблере 6502 безо всяких комментариев. Это само по себе похоже на подвиг: как отметил khim, там «набор команд столь ограничен и крив, что при написании программ возникает в основном вопрос «а как на этом чуде вообще хоть что-то написать»?» Тем не менее, исследователи расковыряли код игры, и выяснили, что лабиринт генерируется следующим образом: для каждой из восьми ячеек генерируемой строки рассматриваются пять уже сгенерированных ячеек (три сверху и две слева), и в соответствии с «магической таблицей» выбирается состояние новой ячейки (проход, стена, либо случайный выбор). Две самые левые ячейки всегда заполнены, и в памяти не хранятся. Правая половина лабиринта — просто зеркальное отражение левой.

Таинственная таблица в сердце неразгаданного алгоритма

Свойства генерируемого лабиринта зависят от того, какое состояние новой ячейки задается для каждой пятерки сгенерированных ранее. Таблица, вшитая в Entombed, немало озадачила исследователей: «Мы не заметили в ней никаких закономерностей, даже когда мы несколькими способами представили ее в виде карты Карно.» Сидли высказался в том же духе: «Для меня она остается загадкой: я так и не смог ее распутать, и использовал ее как черный ящик.» Впрочем, отсутствие закономерностей в таблице — некоторое преувеличение: например, на карте Карно видно, что при c=1 (стена слева сверху от текущей ячейки) не будет генерироваться X=1 (стена в текущей ячейке).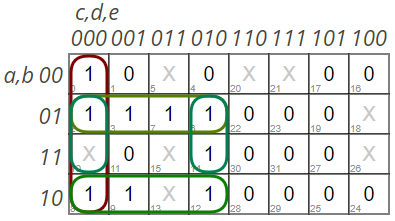



BBC в своем репортаже про «цифровую археологию» прибегла к еще более драматичным преувеличениям: «Таблица составлена поистине гениально: при каждом запуске игры создается новый лабиринт, по которому можно пройти из начала в конец. Если бы значения в этой таблице были хоть немного другими, то скорее всего, лабиринт получался бы непроходимым. Это просто необъяснимо.» Перепост на hackaday.com сформулирован еще увереннее: «Загадочная таблица всегда создает проходимые лабиринты, но стоит в ней поменять любые биты, и головоломка станет неразрешимой.» На самом же деле, и лабиринт не всегда получался связным, как видно на видеозаписи игры; и небольшие изменения в таблице не оказывают заметного влияния на получающиеся лабиринты: я сделал версию на JavaScript, в которой вы можете сами поиграть с «загадочной таблицей» — менять ее прямо «на ходу» и следить, как в результате меняется лабиринт. Вероятно, гарантия связности лабиринта, о которой упоминал и Paul Newell в своем интервью, была потеряна вместе с удаленной частью кода.

Археология видеоигр

John Aycock прокомментировал, как Entombed стала объектом его исследования: он готовил для своих студентов задание на реверс-инжиниринг, и выбрал относительно малоизвестную игру, потому что для популярных игр студенты могли бы найти в сети уже разобранный код. Если в игре, выбранной наугад, встретилась такая выдающаяся находка — не значит ли это, что практически в любой игре того времени найдутся блестящие программистские решения, стоит лишь копнуть поглубже? Стивен Сидли сравнил разработку для Atari 2600, с ее убогим набором команд, 128 байтами ОЗУ, и 76 тактами на каждую строку пикселей, — с «восхождением на Эверест без кислородных баллонов»: сами ограничения платформы вынуждали программистов изобретать гениальные алгоритмы.

«Копнуть поглубже» — это не только метафора. Исследование классических видеоигр осложняется как недолговечностью носителей, на которых они были записаны, так и отношением к старым играм как к неинтересному мусору. В 1983 Atari вывалила на свалку 47 тонн картриджей для Atari 2600 — не меньше десятка полных грузовиков! Раздавленные асфальтовым катком и залитые сверху бетоном, эти картриджи лежали тридцать лет, пока в 2014 «цифровые археологи» не получили разрешение на раскопки и извлечение уцелевших картриджей. Ни один из выкопанных картриджей не работал, но как минимум один из них удалось восстановить, перепаяв компоненты.

Поведение Atari, залившей картриджи бетоном, чтобы защитить их от «расхитителей» — весьма типично для правообладателей, которые легче предадут свои наработки вечному забвению, чем потерпят «упущенную выгоду» от того, что их интеллектуальная собственность кому-то достанется бесплатно. Но возможно, еще не поздно защитить «виртуальный культурный слой» 20-го века, разрешив свободное копирование программ, давно утративших коммерческую ценность?