Недавно вышла интересная статья от FaceBook о том как можно делать неплохой 3D с монокулярных камер. Статья не очень применимая на практике. Но по качеству картинки завораживает:

Посмотрев на это я решил сделать небольшой рассказ о том что в статье творится, куда современные технологии пришли, и что можно ждать от них на практике.

Начнём с основ. Существует несколько способов снять 3D:

• Активная 3д камера (лидар, проекционная, TOF). Излучаем-измеряем.

• Стерео камера. Оцениваем глубину из геометрии.

• Монокулярные. Используем для оценки глубины либо опыт, либо сдвиг камеры.

В этой статье мы будем разбирать монокулярное. В чём его сложность? Да вот:

Эта картинка очень хорошо описывает основную проблему. Даже человек не может оценить глубину с одного ракурса.Что-то может, но точность будет не очень + возможна масса ошибок.

Как с этим борются? Камера должна двигаться, а место действия не должно меняться. Алгоритмы которые могут собрать из это картинку называются  “SLAM”. Логика там более-менее одинаковая (описываю грубо):

• На первом кадре выделяем набор фич и кладём их в общий мешок.

• На каждом новом кадре выделяем фичи, сравниваем их с фичами из мешка.

• Найдя пересекающиеся - можно оценить текущий сдвиг относительно прочих кадров, а для всех фич из мешка - оценить положение

Вот пример того как это работает из далёкого 2014 года (но вообще было и сильно раньше):

У алгоритмов есть одна забавная бага. Вы не можете знать абсолютные расстояния в полученной сцене. Только относительные. 

Но это не сложно исправить замерив хотя бы один объект.

Хорошие SLAM-алгоритмы появились ещё лет десять назад. Сейчас вы можете найти их в AR Core или ARKit, которые доступны почти на каждом телефоне. Вот как это будет выглядеть прямо из коробки без всяких лидаров:

Эти же алгоритмы используются в:

• Алгоритмах восстановления 3Д по серии кадров (фотограмметрия)

• Алгоритмах дополненной реальности для редактирования видео

• Алгоритмах ориентации в дронах

• И прочее и прочее…

Из лучших доступных OpenSource алгоритмов такого плана сейчас есть COLMAP. Он удобно упакован, много исследователей используют его для создания базового решения.
Но в чём проблем таких алгоритмов?

Все SLAM алгоритмы не дают достаточную плотность 3D:

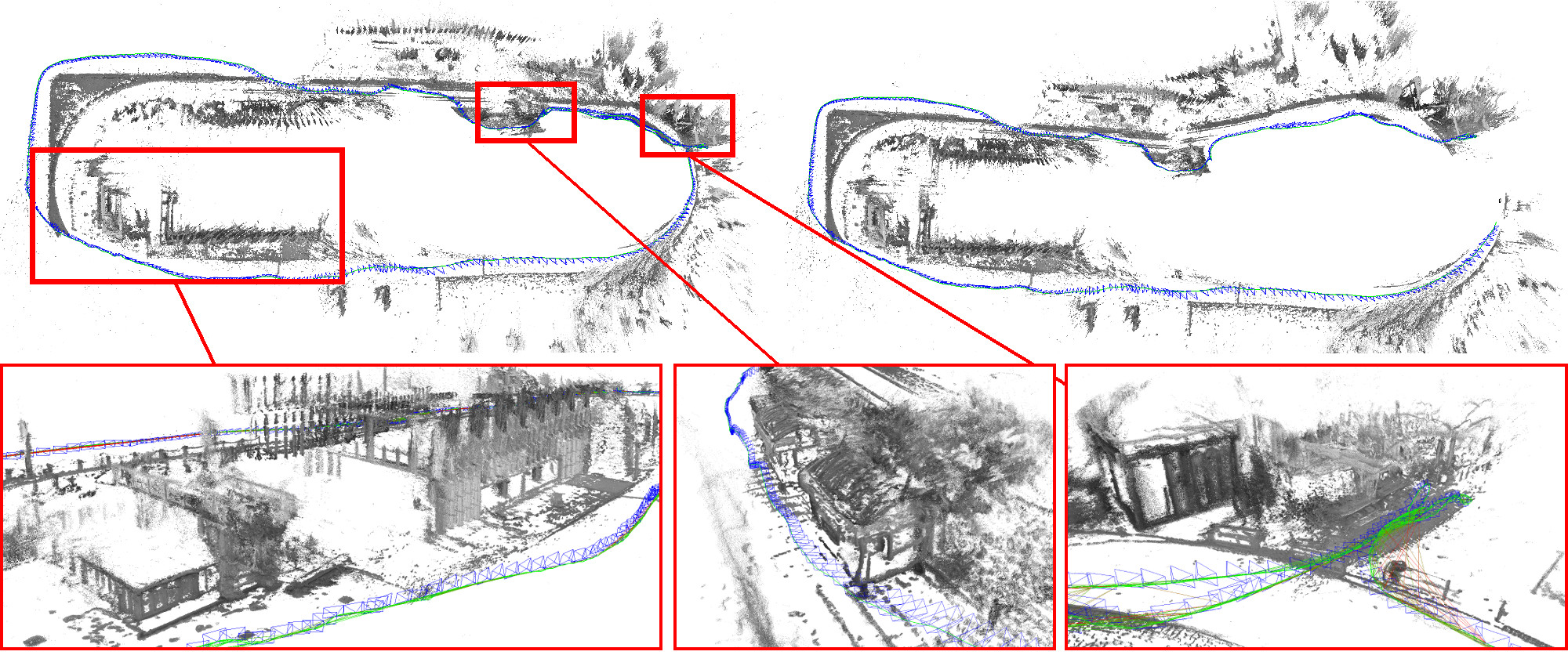
Как с этим борются?

Подходов много. Раньше были аналитические, а сейчас более популярные - через нейронные сети. Собственно, о двух-трех самых популярных и интересных мы и поговорим.
Мы будем говорить именно про самые популярные. Почему не про “самые точные”? Это интересный вопрос. Если мы говорим “самые точные”, то мы должны, например, формализовать по какому датасету сравниваем точности. Таких датасетов много.
Но вот суровый минус - они все специфичные. И зачастую сети имеющие хорошие точности на таких датасетах - работают только на них. Хорошим примером является KITTY:

Сети оптимизированные и хорошо обученные по нему - будут не очень хорошо работать на других данных.

При этом зачастую восстановление 3Д это уже не простой констракт плана “проверить на датасете глубину”, а что-то более сложное, такое как “проверить точность восстановления объекта”, или “оценить точность на всей видеопоследовательности”. И тут уже датасетов будет мало, сложно по ним бенчмаркаться.

Если посмотреть на какой-нибудь сабтаск оценки глубины - Depth Estimation, то по каждому “конкурсу” будет всего одна-две работы.
Так что смысла говорить о самом точном нет. И я буду рассказывать, на свой взгляд о “самом интересном и полезном”, что показывает разные подходы.

MiDaS

Начнём с замечательного MiDaS. Он вышел год назад, и смог инкапсулировать в себя огромное множество идей:

• Смогли одновременно обучаться на множестве датасетов с разнородными данными. На стереофильмах, на данных с датчиков глубины, на сканах местности, и.т.д.

• Натренировали принципиально разные выходы модели для прогнозирования глубины + различные способы смешивания для получения оптимальной оценки.

• Смогли сделать эту модель достаточно быстрой

Кроме того MiDaS доступен из коробки на разных платформах:

• Вот pytorch

• Вот версия под intel

И то и то можно запустить минут за десять. А результат? В первом приближении как-то так:

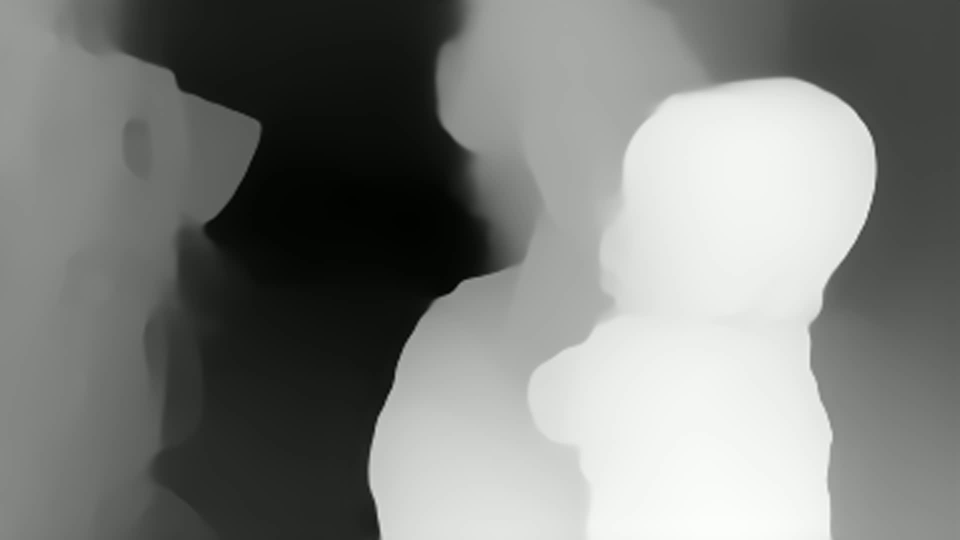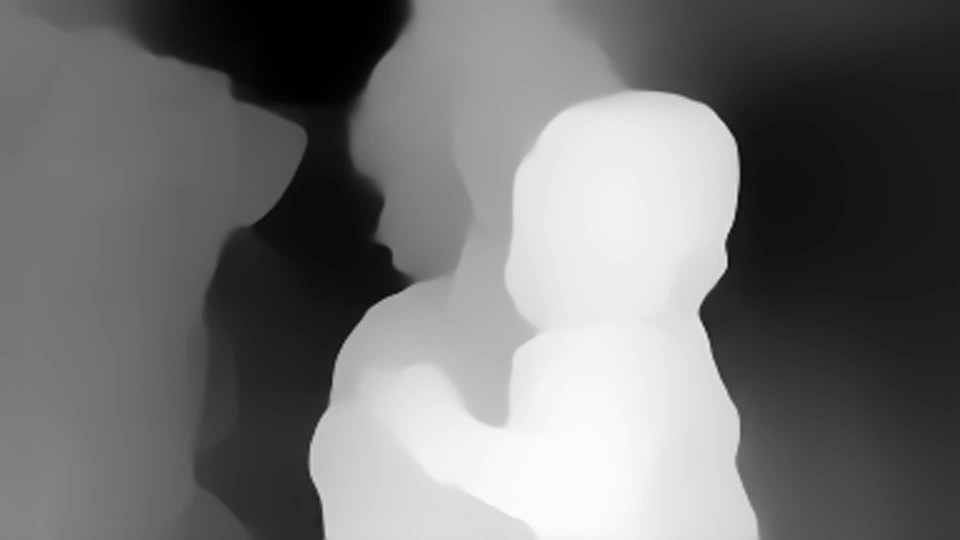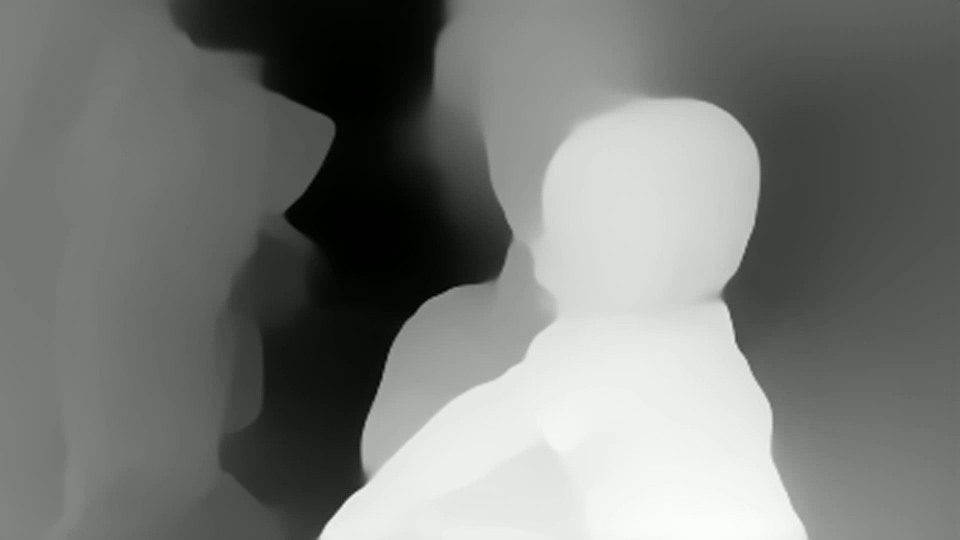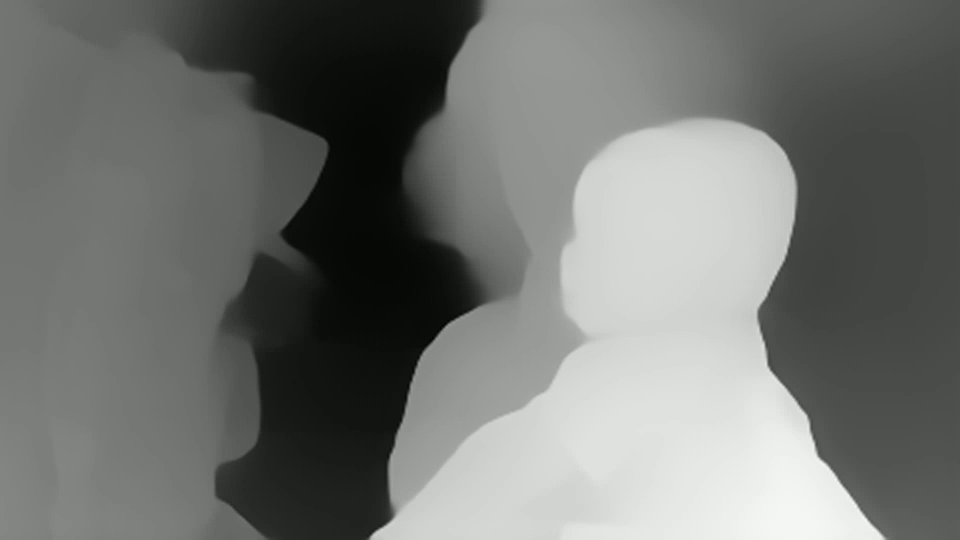
Видно, что тут оценка глубины есть в каждой точке. Но сразу видно что:

• Видна нестабильность глубины от кадра к кадру

• Нет абсолютных значений размера (что типично для монокулярных задач)

• Глубина достаточно неплохо обрабатывается, в том числе для объектов на похожем фоне

Но, естественно, доверять однозначно таким вещам нельзя:

Полный скан

Устранить дрожание во время кадра можно за счёт учёта соседних кадров и нормировки за их счёт. И тут на помочь приходят ранее упомянутые SLAM алгоритмы.С их помощью строят профиль перемещения камеры, делают привязку каждого кадра к общему плану.
Есть несколько алгоритмов которые такое реализуют. Например Атлас и DELTAS

Данные подходы позволяют портировать весь скан в TSDF пространство, и построить полное сканирование. Подходы несколько разны. Первый по мешку точек строит оценку глубины для всей сцены:

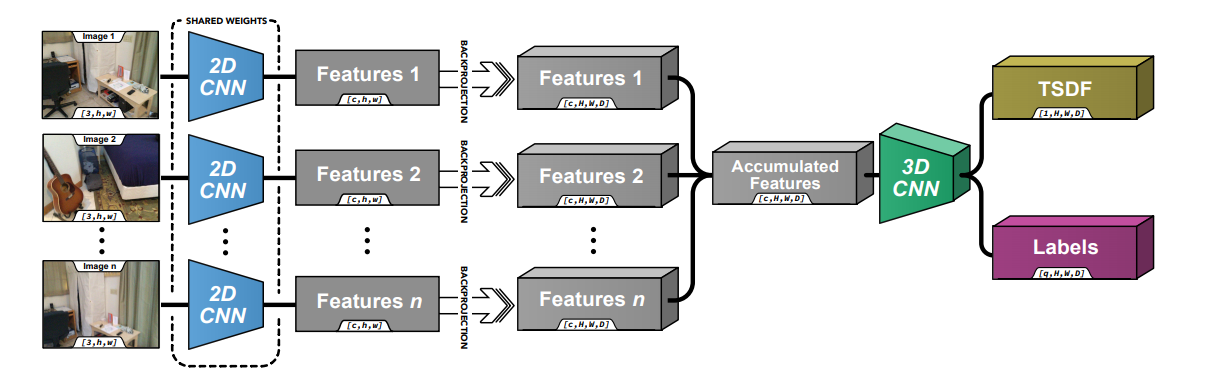
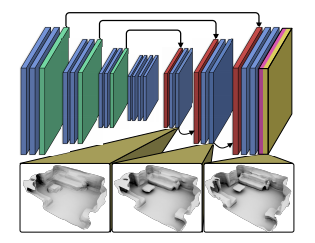
Второй примерно так же, но чуть сложнее:

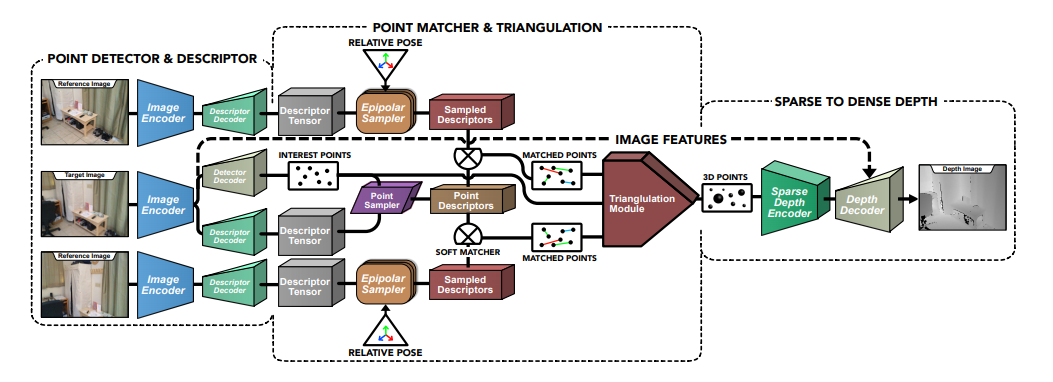
Есть чуть более хитрые подходы, когда нейронная сеть оценивает глубину как Мидас, и проецирует напрямую в TSDF.
Какая точность у таких методов? Конечно куда меньше чем у любой аппаратуры оснащенной нормальным 3D сканером. Например очередной сканер на iPhone’овском лидаре:

Consistent Video Depth Estimation

Можно ли добиться большего, но с монокулярной камеры? Да, можно. Но для этого надо отправляться в сторону алгоритмов которые оценивают глубину по серии кадров в последовательности. Примером такого алгоритма может быть “Consistent Video Depth Estimation”.
Его особенностью является интересный подход, когда берётся два снимка из последовательности, для которых через ранее упомянутый SLAM оценивают сдвиг. После чего эти два снимка служат инпутом для обучения модели под текущее видео:

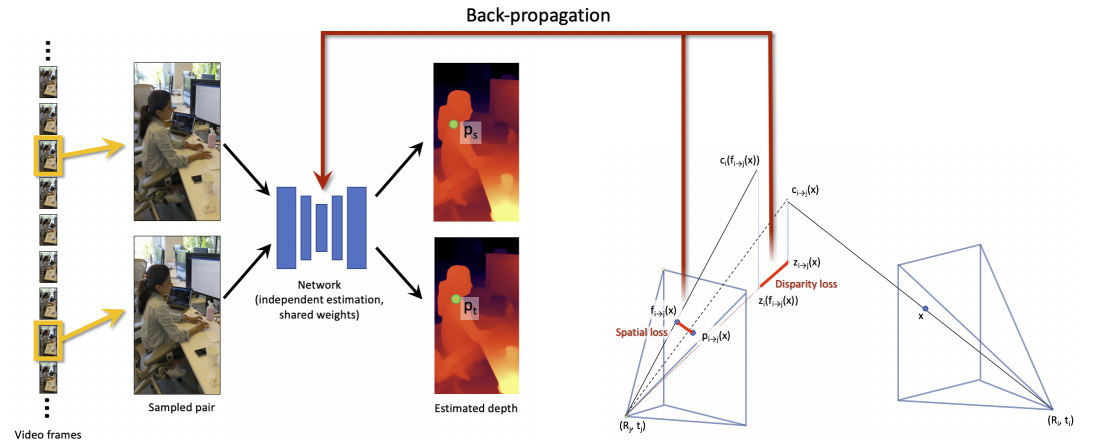
Да-да, для каждого видео обучается (дообучается) отдельная модель.И как-бы основной минус такого подхода - его время. Расчет занимает 4-5 часов на 10-секундное видео. Но результат восхищает:

Почему я привожу тут видео из примеров? Банально. Потому что запустить эту конструкцию, даже при наличии colab  по своему видео я не смог.

Но на текущий момент такая штука показывает State-Of-Art в распознавании глубины в видео. А больше примеров можно посмотреть тут.

В формате видео

Примерно на эту же тему несколько дней назад я делал видео на своем канале. Если вам удобнее воспринимать информацию на слух, то может лучше там смотреть:

Заключение

В целом, на мой взгляд, для серьёзных задач монокулярный depth не нужен. И в будущем, скорее всего, везде где нужен будет хороший depth - проще будет использовать какой-нибудь лидар, благо точность растет, а цена падает. И в лидарах и в стереокамерах вовсю используются те же самые нейросети. Только вот в лидарах и стереокамерах есть оценка реальной глубины по одному кадру - что делает их априори точнее.
Но это не отменяет того что сегодня Monocular Depth уже используется в десятках применений где он удобнее. И, возможно, в будущем, за счёт повышения качества, он станет использоваться ещё чаще.

p.s.

В последнее время делаю много мелких статей/видеороликов. Но так как это не формат Хабра - то публикую их на своём канале (телега, вк). На Хабре обычно публикую, когда рассказ становится уже более самозамкнутым, иногда нужно 2-3 разных мини-рассказа на соседние темы.