Как в коде на C++ прочитать значение double из строки?

std::stringstream in(mystring);
while(in >> x) {
   sum += x;
}

На Intel Skylake с компилятором GCC 8.3, такой код парсит 50 МБ/с. Жёсткие диски запросто обеспечивают последовательное чтение со скоростью в несколько ГБ/с, так что вне всякого сомнения, нас ограничивает не скорость чтения с диска, а именно скорость парсинга. Как его ускорить?

Первое, что напрашивается – отказаться от удобств, предоставляемых потоками в C++, и вызывать strtod(3) напрямую:

do {
    number = strtod(s, &end);
    if(end == s) break;
    sum += number;
    s = end; 
} while (s < theend);

Скорость вырастает до 90 МБ/с; профайлинг показывает, что при чтении из потока выполняется ~1600 инструкций на каждое читаемое число, при использовании strtod – ~1100 инструкций на число. Стандартные библиотеки Си и C++ можно оправдать требованиями универсальности и переносимости; но если ограничиться парсингом только double и только на x64, то можно написать намного более эффективный код: хватит 280 инструкций на число.

Парсинг целых чисел

Начнём с подзадачи: дано восьмизначное десятичное число, и надо перевести его в int. В школе всех нас научили делать это циклом:

int sum = 0;
for (int i = 0; i <= 7; i++)
{
	sum = (sum * 10) + (num[i] - '0');
}
return sum;

Скомпилированный GCC 9.3.1 -O3, у меня этот код обрабатывает 3 ГБ/с. Очевидный способ его ускорить – развернуть цикл; но компилятор это делает и сам.

Обратим внимание, что десятичная запись восьмизначного числа как раз помещается в переменную int64_t: например, строка “87654321” хранится так же, как int64_t-значение 0x3132333435363738 (в первом байте – младшие 8 бит, в последнем – старшие). Это значит, что вместо восьми обращений к памяти мы можем выделять значение каждой цифры сдвигом:

int64_t sum = *(int64_t*)num;
return (sum      & 15) * 10000000 +
    ((sum >> 8)  & 15) * 1000000 +
    ((sum >> 16) & 15) * 100000 +
    ((sum >> 24) & 15) * 10000 +
    ((sum >> 32) & 15) * 1000 +
    ((sum >> 40) & 15) * 100 +
    ((sum >> 48) & 15) * 10 +
    ((sum >> 56) & 15);

Ускорения пока ещё нет; напротив, скорость падает до 1.7 ГБ/с! Пойдём дальше: AND с маской 0x000F000F000F000F даст нам 0x0002000400060008 – десятичные цифры на чётных позициях. Объединим каждую из них со следующей:

sum = ((sum & 0x000F000F000F000F) * 10) + 
      ((sum & 0x0F000F000F000F00) >> 8);

После этого 0x3132333435363738 превращается в 0x00(12)00(34)00(56)00(78) – байты на чётных позициях обнулились, на нечётных – содержат двоичные представления двузначных десятичных чисел.

return (sum        & 255) * 1000000 +
      ((sum >> 16) & 255) * 10000 +
      ((sum >> 32) & 255) * 100 +
      ((sum >> 48) & 255);

— завершает преобразование восьмизначного числа.

Тот же самый трюк можно повторить и с парами двузначных чисел:

sum = ((sum & 0x0000007F0000007F) * 100) +
      ((sum >> 16) & 0x0000007F0000007F);

— 0x00(12)00(34)00(56)00(78) превращается в 0x0000(1234)0000(5678);
и с получившейся парой четырёхзначных:

return ((sum & 0x3FFF) * 10000) + ((sum >> 32) & 0x3FFF);

— 0x00(12)00(34)00(56)00(78) превращается в 0x00000000(12345678). Младшая половина полученного int64_t – это и есть искомый результат. Несмотря на заметное упрощение кода (три умножения вместо семи), скорость парсинга (2.6 ГБ/с) остаётся хуже, чем у наивной реализации.

Но объединение пар цифр можно ещё упростить, если заметить, что следующее действие применит маску 0x007F007F007F007F, а значит, в обнуляемых байтах можно оставить любой мусор:

sum = ((sum & 0x0?0F0?0F0?0F0?0F) * 10) + ((sum & 0x0F??0F??0F??0F??) >> 8) =
   = (((sum & 0x0F0F0F0F0F0F0F0F) * 2560)+ (sum & 0x0F0F0F0F0F0F0F0F)) >> 8 =
    = ((sum & 0x0F0F0F0F0F0F0F0F) * 2561) >> 8;

В упрощённом выражении одна маска вместо двух, и нет сложения. Точно так же упрощаются и два оставшихся выражения:

sum = ((sum & 0x00FF00FF00FF00FF) * 6553601) >> 16;
return((sum & 0x0000FFFF0000FFFF) * 42949672960001) >> 32;

Этот трюк получил название SIMD within a register (SWAR): с использованием него скорость парсинга вырастает до 3.6 ГБ/с.

Аналогичным SWAR-трюком можно проверить, является ли восьмисимвольная строка восьмизначным десятичным числом:

return ((val & 0xF0F0F0F0F0F0F0F0) |
      (((val + 0x0606060606060606) & 0xF0F0F0F0F0F0F0F0) >> 4))
            == 0x3333333333333333;

Устройство double

Стандарт IEEE отвёл внутри этих чисел 52 бита на мантиссу и 11 на экспоненту; это значит, что число хранится в виде $$, где $$ и $$. В частности, это значит, что в десятичной записи double только старшие 17 цифр имеют значение; более младшие разряды никак не могут повлиять на значение double. Даже 17 значащих цифр – это намного больше, чем может понадобиться для любого практического применения:



Немного усложняют работу денормализованные числа (от $$ до $$ с соответственно меньшим числом значащих битов в мантиссе) и требования к округлению (любое десятичное число должно представляться ближайшим двоичным, а если число попало точно в середину между ближайшими двоичными, то предпочтение отдаётся чётной мантиссе). Всё это гарантирует, что если компьютер A переведёт число X в десятичную строку с 17 значащими цифрами, то любой компьютер B, прочитав эту строку, получит то же самое число X, бит в бит – независимо от того, совпадают ли на A и на B модели процессоров, ОС, и языки программирования. (Представьте себе, как увлекательно было бы отлаживать код, если бы ошибки округления на разных компьютерах были разными.) Из-за требований к округлению возникают недоразумения, недавно упомянутые на Хабре: десятичная дробь 0.1 представляется в виде ближайшей к ней двоичной дроби $$, равной в точности 0.1000000000000000055511151231257827021181583404541015625; 0.2 – в виде $$, равной в точности 0.200000000000000011102230246251565404236316680908203125; но их сумма – не ближайшая к 0.3 двоичная дробь: приближение снизу $$ = 0. 299999999999999988897769753748434595763683319091796875 оказывается более точным. Поэтому стандарт IEEE требует, чтобы при сложении 0.1+0.2 получался результат, отличный от 0.3.

Парсинг double

Прямолинейное обобщение целочисленного алгоритма заключается в итеративных умножениях и делениях на 10.0 – в отличие от парсинга целых чисел, здесь необходимо обрабатывать цифры от младших к старшим, чтобы ошибки округления старших цифр «скрывали» ошибки округления младших. Вместе с тем, парсинг мантиссы легко сводится к парсингу целых чисел: достаточно поменять нормализацию, чтобы воображаемая двоичная точка стояла не в начале мантиссы, а в конце; получившееся 53-битное целое число умножить или поделить на нужную степень десятки; и наконец, отнять 52 от экспоненты, т.е. перенести точку на 52 бита влево – туда, где она должна быть по стандарту IEEE. Вдобавок стоит заметить три важных факта:

1. Достаточно научиться множить либо делить на 5, а умножение либо деление на 2 – это просто инкремент либо декремент экспоненты;
2. Деление uint64_t на 5 заменяется умножением на 0xcccccccccccccccd и сдвигом вправо на 66 битов, пользуясь тем, что $$ и поэтому все 64 бита результата будут верными (с округлением вниз);
3. Возможны лишь несколько сотен значений десятичной экспоненты – от $$ до $$; это значит, что можно приготовить заранее таблицу из 309 степеней пятёрки, 324 степеней 0xcccccccccccccccd, и вместо итеративного умножения брать сразу готовый результат. (От каждой степени нам нужны только 53 значащих бита и слагаемое к экспоненте; поскольку целочисленное умножение даёт 128-битный результат, то произведение 53-битной мантиссы и 53-битной табличной степени вычисляется точно.) Эти 633 степени можно было бы хранить сразу в виде double (вас вряд ли удивит, что вышеупомянутая двоичная мантисса дроби ?, равная 7205759403792794 – это и есть 0xcccccccccccccccd, округлённое до 53 битов), и переводить мантиссу в формат double до умножения на табличную степень; но это ограничило бы точность вычисления 53 битами, чего недостаточно для соответствия требованиям к округлению. В действительности, для округления результата к ближайшему двоичному числу, 64 бита мантиссы множатся на 64 бита табличной степени, и если этого оказывается недостаточно, то умножение повторяется со 128-битным значением табличной степени. В крайне редких случаях для необходимой точности может не хватить и второго умножения.

Сложность стандартного округления в том, что чтобы узнать, что результат попал точно в середину между ближайшими двоичными дробями, нам не только нужны 54 значащих бита результата (нулевой младший бит означает «всё в порядке», единичный – «попали в середину»), но и нужно следить, было ли после младшего бита ненулевое продолжение. В частности, это значит, что рассмотрения в десятичной записи числа только 17 старших цифр недостаточно: они определяют двоичную мантиссу лишь с точностью до ±1, и для выбора нужного направления округления придётся рассматривать более младшие цифры. Например, 10000000000000003 и 10000000000000005 – это одно и то же значение double (равное 10000000000000004), а 10000000000000005.00(много нулей)001 – это уже другое значение (равное 10000000000000006).

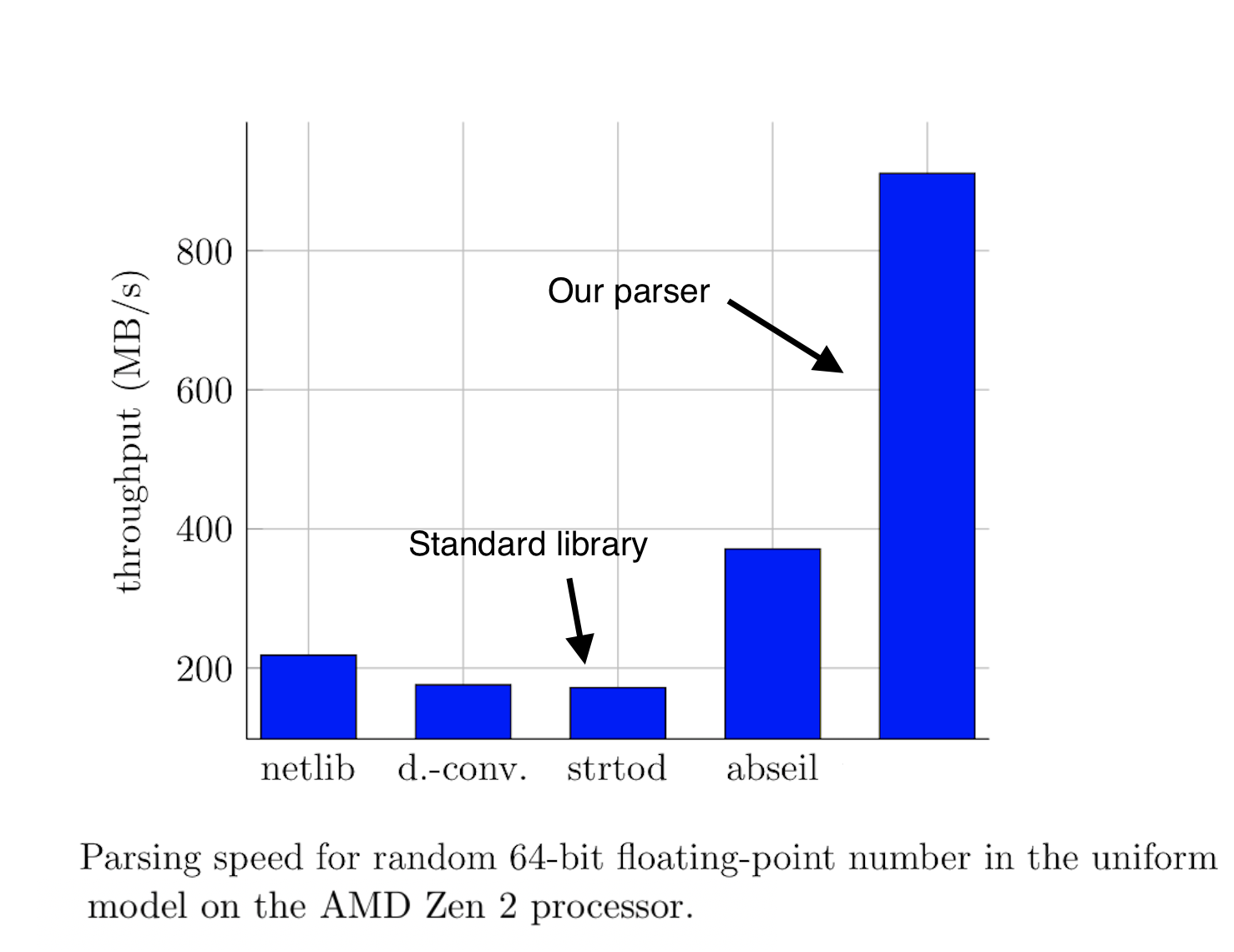
Профессор Заочного квебекского университета (TELUQ) Daniel Lemire, придумавший этот парсер, опубликовал его на гитхабе. Эта библиотека предоставляет две функции from_chars: одна парсит строку в double, другая – во float. Его эксперименты показали, что в 99.8% случаев достаточно рассматривать 19 значащих десятичных цифр (64 бита): если для двух последовательных значений 64-битной мантиссы получается одно и то же конечное значение double, то это и есть верное значение. Лишь в 0.2% случаев, когда эти два значения не совпадают, выполняется более сложный и более универсальный код, реализующий всегда корректное округление.