10.03.2021 10:45
Pixonic 14 7800 Источник
Рисунок 1
Рисунок 1

В этом посте мы заглянем под капот алгоритмов компьютерной графики, пошагово разберем основные принципы трассировки лучей и напишем ее простую реализацию на Python. Никаких сторонних графических библиотек — только NumPy и голый код в компиляторе.

Примечание: Эта статья ни в коем случае не является полным руководством/объяснением трассировки лучей, поскольку эта тема слишком обширна, а скорее просто введением для любопытствующих.

Предпосылки

Нам понадобится только самая базовая векторная геометрия:

  • Пусть у нас есть две точки A и B — независимо от размерности: 1, 2, 3,…, n, — тогда вектор, идущий от A к B, может быть найден путем вычисления B — A (поэлементно);

  • Длину вектора — независимо от его размерности — можно найти, вычислив квадратный корень из суммы возведенных в квадрат компонентов. Длина вектора v обозначается ||v||;

  • Единичный вектор — это вектор длины 1: ||v|| = 1;

  • Для данного вектора другой вектор, идущий в том же направлении, но имеющий длину 1, может быть найден путем деления каждого компонента первого вектора на его длину — это называется нормализацией: u = v/||v||;

  • Скалярное произведение для векторов вычисляется как: <v, v> = ||v||?.

Алгоритм трассировки лучей

Трассировка лучей — это метод рендеринга, который имитирует путь света и пересечения с объектами и позволяет создавать изображения с высокой степенью реализма. Более оптимизированные варианты этого алгоритма используются в видеоиграх.

Чтобы объяснить работу этого алгоритма, сначала нужно настроить сцену:

  • Трехмерное пространство (мы собираемся использовать три координаты для позиционирования объектов в пространстве);

  • Объекты в этом пространстве (поскольку мы собираемся воспроизвести рис. 1, то возьмем в качестве объектов сферы);

  • Источник света (в нашем случае это одна точка, излучающая свет во всех направлениях);

  • Камера для наблюдения за сценой;

  • Экран, через который камера смотрит на объекты (четыре точки для четырех углов прямоугольного экрана).

Рисунок 2
Рисунок 2

Экран — это некая определенная вами геометрическая фигура (например, прямоугольник 3x2). Но сами по себе цифры 3 и 2 ни о чем нам не говорят и действительно начинают приобретать какое-то значение только при сравнении их с размерами других объектов. Здесь важно то, как вы разделите ваш прямоугольник на более мелкие квадраты (пиксели), как на рисунке выше. Это определит размер конечного изображения. Другими словами, можно взять прямоугольник 3x2 и разделить его на 300x200 пикселей.

Напишем алгоритм трассировки лучей с учетом заданной сцены:

для каждого пикселя p(x, y, z) экрана:

   ассоциировать черный цвет с p

   если луч (линия), начинающийся от камеры и идущий к точке p, пересекает любой объект сцены, то:

       вычислить точку пересечения с ближайшим объектом

       если между точкой пересечения и источником света нет объекта, тогда:

           рассчитать цвет точки пересечения

           сопоставить цвет точки пересечения с p

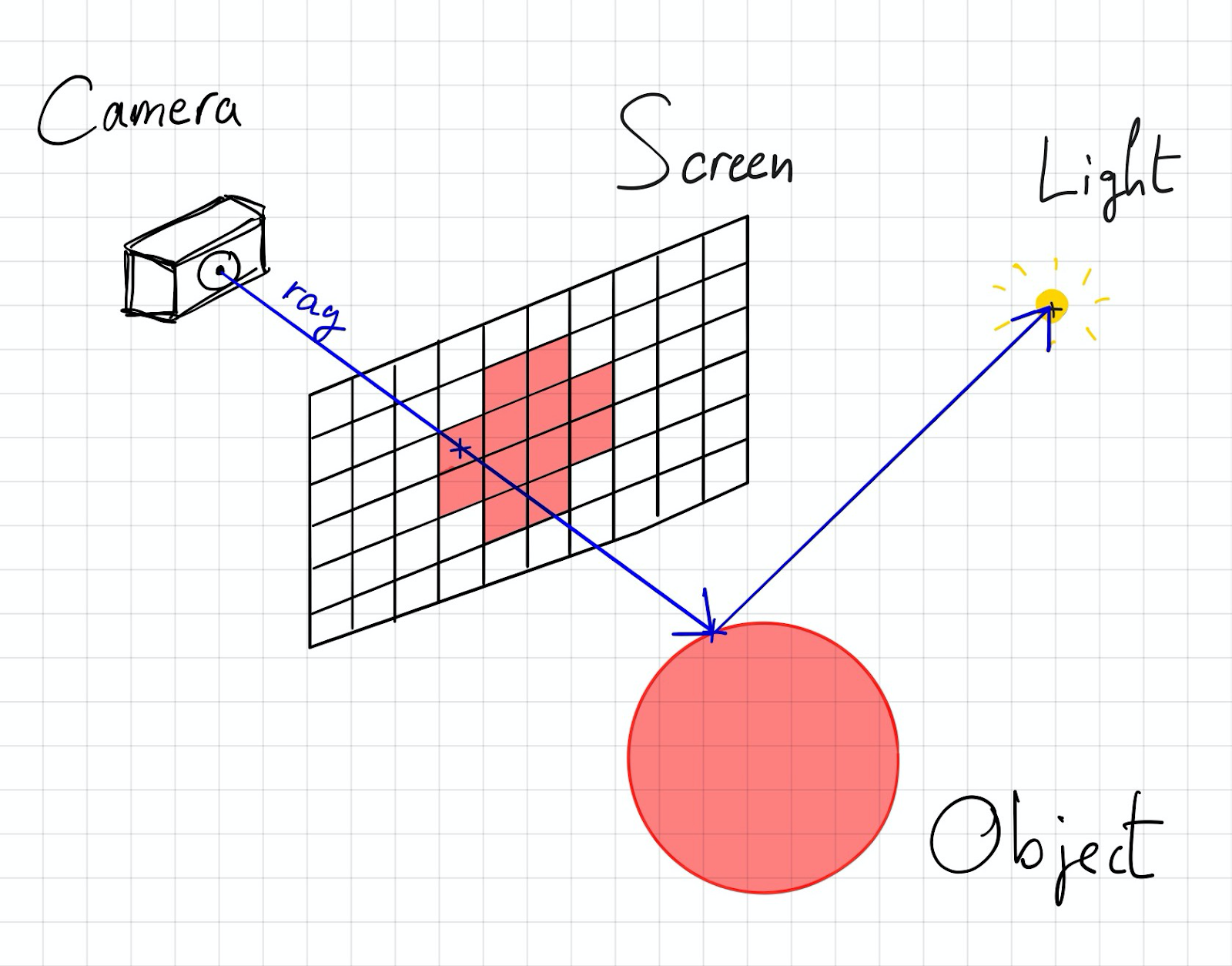
Рисунок 3
Рисунок 3

Обратите внимание, что этот процесс на деле оказывается обратным реальному освещению. Ведь реальный свет выходит из источника во всех направлениях, отражается от объектов и попадает в камеру. Однако, поскольку не все лучи, выходящие из источника света, попадут в камеру, трассировка лучей выполняет обратный процесс для экономии времени вычислений (отслеживает лучи от камеры обратно к источнику света).

Настройка сцены

Перед тем, как начать писать код, нам нужно настроить сцену. В первую очередь определимся, где расположены камера и экран. Для этой цели примем некоторые упрощения, совместив объекты с координатными осями.

Рисунок 4
Рисунок 4

Допустим, камера расположена в точке (x = 0, y = 0, z = 1), а экран является частью плоскости, образованной осями x и y. Теперь мы можем написать скелет нашего кода.

Посмотреть код
import numpy as np
import matplotlib.pyplot as plt
width = 300
height = 200
camera = np.array([0, 0, 1])
ratio = float(width) / height
screen = (-1, 1 / ratio, 1, -1 / ratio) # слева, сверху, справа, снизу
image = np.zeros((height, width, 3))
for i, y in enumerate(np.linspace(screen[1], screen[3], height)):
    for j, x in enumerate(np.linspace(screen[0], screen[2], width)):
        # image[i, j] = ...
        print("progress: %d/%d" % (i + 1, height))
plt.imsave('image.png', image)

  • Камера — это просто точка, имеющая три координаты;

  • С другой стороны, экран определяется четырьмя числами (или двумя точками): слева, сверху, справа, снизу. Он находится в диапазоне от -1 до 1 в направлении x и от -1/ratio до 1/ratio в направлении y, где ratio — ширина изображения, деленная на его высоту. Это вытекает из того, что мы хотим, чтобы экран имел такое же соотношение сторон, что и фактическое изображение. При такой настройке экрана будет получено соотношение сторон (ширина к высоте): 2 /(2/ratio) = ratio, которое и является соотношением сторон желаемого изображения 300x200;

  • Цикл состоит из разделения экрана на точки в направлениях x и y, затем вычисляется цвет текущего пикселя;

  • Полученный код создаст — как и ожидалось на данном этапе — черное изображение. 

Пересечение лучей

Следующий шаг алгоритма: если луч (линия), начинающийся от камеры и проходящий к точке p, пересекает объект сцены, тогда...

Разобьем его на две части. И начнем с определения того, какой луч (линия) начинается от камеры и идет к точке p?

Определение луча

Когда мы говорим «луч», на самом деле мы имеем в виду скорее «линию». Всякий раз при работе с геометрией лучше отдать предпочтение векторам, чем реальным линейным уравнениям: с ними легче работать, и они гораздо менее подвержены ошибкам, таким как деление на ноль.

Итак, поскольку луч начинается от камеры и идет в направлении текущего целевого пикселя, мы можем определить единичный вектор, указывающий в том же направлении. Поэтому мы определяем наш луч следующим уравнением:

Помните, что камера и пиксель — это 3D-точки. При t = 0 вы окажетесь в положении камеры, но с увеличением t будете удаляться от нее в направлении пикселя. Это параметрическое уравнение, которое даст точку вдоль линии для любого t.

Конечно, точно так же мы можем переписать уравнение и определить луч, который начинается в исходной точке (O) и идет к месту назначения (D) как:

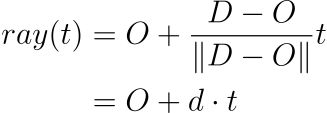
Для удобства определим d как вектор направления.

Теперь мы можем добавить к нашему коду вычисление луча:

Посмотреть код
import numpy as np
import matplotlib.pyplot as plt
def normalize(vector):
    return vector / np.linalg.norm(vector)
width = 300
height = 200
camera = np.array([0, 0, 1])
ratio = float(width) / height
screen = (-1, 1 / ratio, 1, -1 / ratio) # слева, сверху, справа, снизу
image = np.zeros((height, width, 3))
for i, y in enumerate(np.linspace(screen[1], screen[3], height)):
    for j, x in enumerate(np.linspace(screen[0], screen[2], width)):
        pixel = np.array([x, y, 0])
        origin = camera
        direction = normalize(pixel - origin)
        # image[i, j] = ...
    print("progress: %d/%d" % (i + 1, height))
plt.imsave('image.png', image)

  • Мы добавили в код функцию normalize(vector), которая возвращает... собственно, нормализованный вектор;

  • Также мы добавили вычисление исходной точки и направления, которые вместе определяют луч. Обратите внимание, что пиксель имеет координату z = 0, поскольку он лежит на экране, который находится в плоскости, образованной осями x и y;

Теперь перейдем ко второй части, где луч пересекает объект сцены. Для простоты будем использовать только сферы.

Определение сферы

Сфера — довольно простой математический объект. Она определяется как набор точек, находящихся на одинаковом расстоянии r (радиус) от заданной точки (центра).

Следовательно, с учетом центра C сферы и ее радиуса r произвольная точка X лежит на сфере тогда, когда:

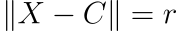
Для удобства возведем обе стороны в квадрат, чтобы избавиться от квадратного корня, обусловленного величиной X — C:

После этого мы сможем определить некоторые сферы сразу после объявления экрана:

objects = [
   { 'center': np.array([-0.2, 0, -1]), 'radius': 0.7 },
   { 'center': np.array([0.1, -0.3, 0]), 'radius': 0.1 },
   { 'center': np.array([-0.3, 0, 0]), 'radius': 0.15 }
]

Теперь вычислим пересечение луча и сферы.

Пересечение со сферой

Мы знаем уравнение лучей и знаем, какому условию должна удовлетворять точка, чтобы она лежала на сфере. Все, что нам нужно сделать, это подставить одно уравнение в другое и решить его относительно t. То есть, найти ответ на вопрос: для какого t точка луча ray(t) окажется на сфере?

Это обычное квадратное уравнение, которое просто решается относительно t. Мы будем вызывать коэффициенты, связанные с t?, t?, t?, a, b и c, соответственно. Вычислим дискриминант этого уравнения:

Поскольку направление d является единичным вектором, получим a = 1. После вычисления дискриминанта у нас есть три варианта:

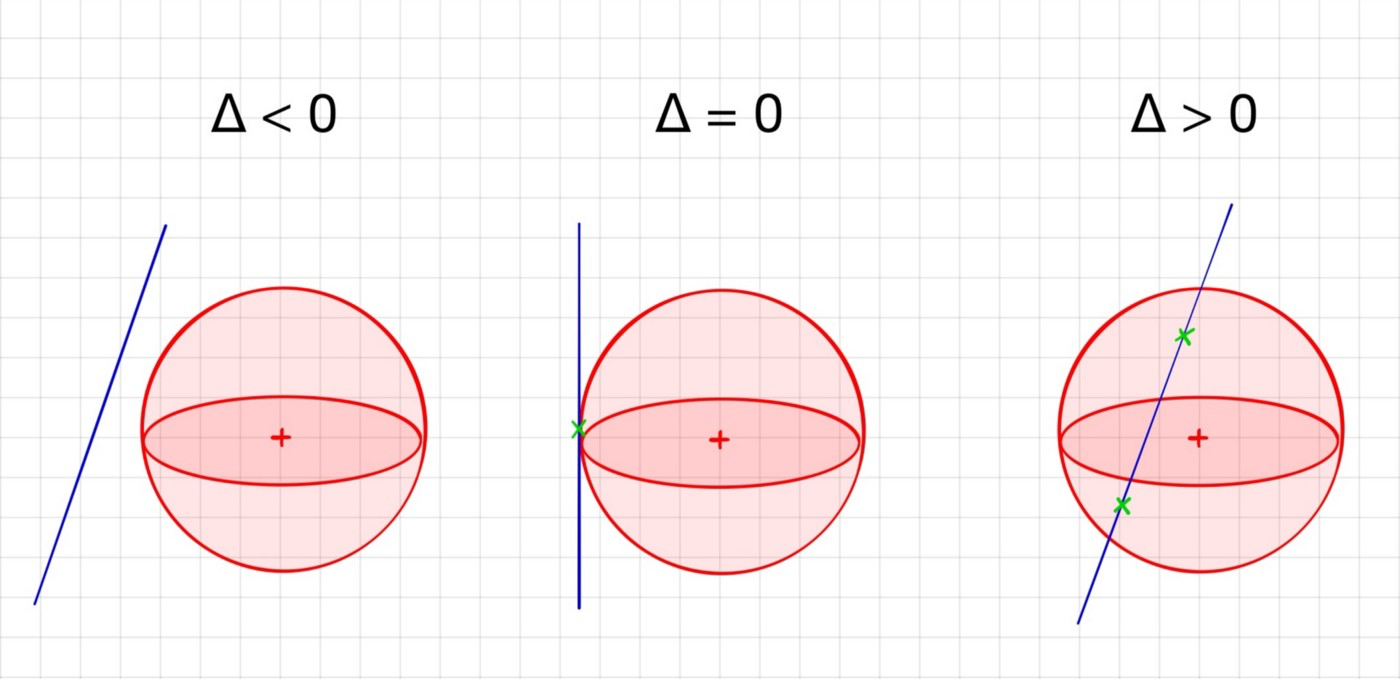
Рисунок 5
Рисунок 5

Для обнаружения пересечений будем использовать только третий случай. Запишем функцию, отвечающую за обнаружение пересечения луча и сферы. Она возвращает расстояние от начала луча до ближайшей точки пересечения, если луч действительно пересекает сферу, иначе возвращает None:

Посмотреть код
def sphere_intersect(center, radius, ray_origin, ray_direction):
   b = 2 * np.dot(ray_direction, ray_origin — center)
   c = np.linalg.norm(ray_origin — center) ** 2 — radius ** 2
   delta = b ** 2 — 4 * c
   if delta > 0:
       t1 = (-b + np.sqrt(delta)) / 2
       t2 = (-b — np.sqrt(delta)) / 2
       if t1 > 0 and t2 > 0:
           return min(t1, t2)
   return None

Обратите внимание, что мы возвращаем только ближайшее пересечение из двух тогда, когда оба t1 и t2 положительны. Это связано с тем, что ответ уравнения может быть отрицательным, и в таком случае луч, пересекающий сферу, будет иметь не d в качестве вектора направления, а -d (например, если сфера находится за камерой и экраном).

Ближайший пересекаемый объект

Пока мы все еще не выполнили инструкцию из псевдокода: если луч (линия), начинающийся от камеры и идущий к точке p, пересекает любой объект сцены, то [...]. Теперь нам нужно вычислить точку пересечения с ближайшим объектом.

Напишем функцию, которая использует sphere_intersect() для поиска ближайшего объекта, с которым пересекается луч, если он существует. Просто перебираем все сферы, ищем пересечения и сохраняем ближайшую сферу:

Посмотреть код
def nearest_intersected_object(objects, ray_origin, ray_direction):
   distances = [sphere_intersect(obj['center'], obj['radius'], ray_origin, ray_direction) for obj in objects]
   nearest_object = None
   min_distance = np.inf
   for index, distance in enumerate(distances):
       if distance and distance < min_distance:
           min_distance = distance
           nearest_object = objects[index]
   return nearest_object, min_distance

При вызове функции, если nearest_object = None, луч не пересекает никакого объекта, иначе его значением является ближайший пересекаемый объект, и мы получаем min_distance — расстояние от начала луча до точки пересечения.

Точка пересечения

Чтобы вычислить точку пересечения, используем предыдущую функцию:

nearest_object, distance = nearest_intersected_object(objects, o, d)
if nearest_object:
   intersection_point = o + d * distance

В результате получаем следующий код:

Посмотреть код
import numpy as np
import matplotlib.pyplot as plt
def normalize(vector):
   return vector / np.linalg.norm(vector)
def sphere_intersect(center, radius, ray_origin, ray_direction):
   b = 2 * np.dot(ray_direction, ray_origin — center)
   c = np.linalg.norm(ray_origin — center) ** 2 — radius ** 2
   delta = b ** 2 — 4 * c
   if delta > 0:
       t1 = (-b + np.sqrt(delta)) / 2
       t2 = (-b — np.sqrt(delta)) / 2
       if t1 > 0 and t2 > 0:
           return min(t1, t2)
   return None
def nearest_intersected_object(objects, ray_origin, ray_direction):
   distances = [sphere_intersect(obj['center'], obj['radius'], ray_origin, ray_direction) for obj in objects]
   nearest_object = None
   min_distance = np.inf
   for index, distance in enumerate(distances):
       if distance and distance < min_distance:
           min_distance = distance
           nearest_object = objects[index]
   return nearest_object, min_distance
width = 300
height = 200
camera = np.array([0, 0, 1])
ratio = float(width) / height
screen = (-1, 1 / ratio, 1, -1 / ratio) # слева, сверху, справа, снизу
objects = [
   { 'center': np.array([-0.2, 0, -1]), 'radius': 0.7 },
   { 'center': np.array([0.1, -0.3, 0]), 'radius': 0.1 },
   { 'center': np.array([-0.3, 0, 0]), 'radius': 0.15 }
]
image = np.zeros((height, width, 3))
for i, y in enumerate(np.linspace(screen[1], screen[3], height)):
   for j, x in enumerate(np.linspace(screen[0], screen[2], width)):
       pixel = np.array([x, y, 0])
       origin = camera
       direction = normalize(pixel — origin)
       # проверка пересечений
       nearest_object, min_distance = nearest_intersected_object(objects, origin, direction)
       if nearest_object is None:
           continue
       # вычисления пересечений между лучом и ближайшим объектом
       intersection = origin + min_distance * direction
       # image[i, j] = ...
       print("%d/%d" % (i + 1, height))
plt.imsave('image.png', image)

Пересечения света

Итак, мы нашли прямую линию, идущую от камеры к объекту, и знаем, что это за объект, а также на какую часть объекта мы смотрим. Но мы пока не знаем, освещена ли вообще эта конкретная точка. Возможно, свет не попадает конкретно на нее, и нет необходимости производить расчеты дальше, потому что мы ее не видим. Следовательно, следующий шаг — проверить, нет ли никаких посторонних объектов между точкой пересечения и источником света.

У нас уже есть функция, которая нам может помочь: near_intersected_object(). И мы хотим знать, пересекает ли луч, который начинается в точке пересечения и идет к свету, объект сцены перед тем, как пересечь свет. Это практически та же задача, что мы решали раньше: нам просто нужно изменить начало и направление луча. Во-первых, нам нужно определить свет. Можно сделать это сразу вместе с объявлением объектов:

light = { 'position': np.array([5, 5, 5]) }

Чтобы проверить, затеняет ли объект точку пересечения, мы должны пропустить луч, который начинается в точке пересечения и идет к свету, и посмотреть, действительно ли ближайший возвращенный объект оказывается ближе, чем свет, к точке пересечения (другими словами, находится ли он между ними).

# ...
intersection = origin + min_distance * direction
intersection_to_light = normalize(light['position'] — intersection)
_, min_distance = nearest_intersected_object(objects, intersection, intersection_to_light)
intersection_to_light_distance = np.linalg.norm(light['position'] — intersection)
is_shadowed = min_distance < intersection_to_light_distance

Что ж, это так не сработает. Нужно сделать небольшую корректировку. Если мы используем точку пересечения в качестве источника нового луча, мы можем в конечном итоге обнаружить сферу, на которой мы сейчас находимся, как объект между точкой пересечения и источником света. Быстрое и широко используемое решение этой проблемы — сделать небольшой шаг, который уводит нас от поверхности сферы. Обычно для этого вычисляется вектор нормали к поверхности и производится отступ в направлении этой нормали.

Рисунок 6
Рисунок 6

Этот трюк используется не только для сфер, но и для любых объектов.

Следовательно, правильный код будет таким:

Посмотреть код
# ...
intersection = origin + min_distance * direction
normal_to_surface = normalize(intersection — nearest_object['center'])
shifted_point = intersection + 1e-5 * normal_to_surface
intersection_to_light = normalize(light['position'] — shifted_point)
_, min_distance = nearest_intersected_object(objects, shifted_point, intersection_to_light)
intersection_to_light_distance = np.linalg.norm(light['position'] — intersection)
is_shadowed = min_distance < intersection_to_light_distance
if is_shadowed:
   continue

Модель отражения Блинна-Фонга

Итак, мы знаем, что луч света попал на объект, а отражение луча — прямо в камеру. Вопрос: что увидит камера? На него и пытается ответить модель Блинна-Фонга.

Модель Блинна-Фонга — это приближение к модели Фонга, требующее меньших вычислительных затрат.

Согласно этой модели, любой материал имеет четыре свойства:

  • Фоновый цвет (Ambient color): цвет, который имеет объект в отсутствие света;

  • Рассеянный цвет (Diffuse color): цвет, наиболее близкий к тому, что мы себе представляем;

  • Зеркальный цвет (Specular color): цвет блестящей части объекта, когда свет попадает на нее. В большинстве случаев это белый цвет;

  • Блеск (Shininess): коэффициент, показывающий, насколько блестящим является объект.

Примечание: Все цвета представлены в RGB в диапазоне 0 – 1.

Рисунок 7
Рисунок 7

Добавим эти свойства к сферам:

objects = [
   { 'center': np.array([-0.2, 0, -1]), 'radius': 0.7, 'ambient': np.array([0.1, 0, 0]), 'diffuse': np.array([0.7, 0, 0]), 'specular': np.array([1, 1, 1]), 'shininess': 100 },
   { 'center': np.array([0.1, -0.3, 0]), 'radius': 0.1, 'ambient': np.array([0.1, 0, 0.1]), 'diffuse': np.array([0.7, 0, 0.7]), 'specular': np.array([1, 1, 1]), 'shininess': 100 },
   { 'center': np.array([-0.3, 0, 0]), 'radius': 0.15, 'ambient': np.array([0, 0.1, 0]), 'diffuse': np.array([0, 0.6, 0]), 'specular': np.array([1, 1, 1]), 'shininess': 100 }
]

В нашем примере сферы имеют цвета красный, пурпурный и зеленый, соответственно.

Модель Блинн-Фонга утверждает, что свет также имеет три цветовых свойства: фоновый цвет, рассеянный и зеркальный. Их тоже добавим к модели:

light = { 'position': np.array([5, 5, 5]), 'ambient': np.array([1, 1, 1]), 'diffuse': np.array([1, 1, 1]), 'specular': np.array([1, 1, 1]) }

Учитывая эти свойства, модель Блинна-Фонга рассчитывает освещенность точки следующим образом:

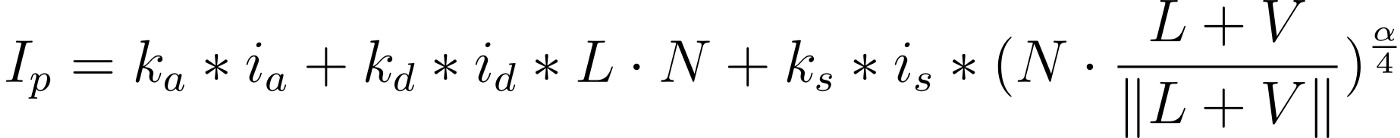
где

  • ka, kd, ks — фоновое, рассеянное, зеркальное свойства объекта;

  • ia, id, is — фоновое, рассеянное, зеркальное свойства света;

  • L — единичный вектор направления от точки пересечения к свету;

  • N — единичный вектор нормали к поверхности объекта в точке пересечения;

  • V — единичный вектор направления от точки пересечения к камере;

  • ? — блеск объекта.

Посмотреть код
# ...
if is_shadowed:
   break

# RGB
illumination = np.zeros((3))

# ambiant
illumination += nearest_object['ambient'] * light['ambient']

# diffuse
illumination += nearest_object['diffuse'] * light['diffuse'] * np.dot(intersection_to_light, normal_to_surface)

# specular
intersection_to_camera = normalize(camera — intersection)
H = normalize(intersection_to_light + intersection_to_camera)
illumination += nearest_object['specular'] * light['specular'] * np.dot(normal_to_surface, H) ** (nearest_object['shininess'] / 4)
image[i, j] = np.clip(illumination, 0, 1)

Обратите внимание, что в конце мы определяем цвет между 0 и 1, чтобы убедиться, что он находится в правильном диапазоне.

Запускаем код

Увеличим ширину и высоту для получения более высокого разрешения (ценой увеличения времени вычислений).

Рисунок 8
Рисунок 8

Можно заметить две вещи, которые отличают результат от первого изображения, показанного в начале:

  • Серый пол отсутствует;

  • Отсутствие отражений.

Фейковая плоскость

В идеале мы должны создать другой тип объекта — плоскость, но поскольку мы достаточно ленивы, то можем просто добавить другую сферу. Ведь если вы стоите на сфере, имеющей бесконечно большой радиус (по сравнению с вашим размером), тогда вам будет казаться, что вы стоите на плоской поверхности.

Добавим эту сферу в список объектов и снова выполним рендеринг:

{ 'center': np.array([0, -9000, 0]), 'radius': 9000 — 0.7, 'ambient': np.array([0.1, 0.1, 0.1]), 'diffuse': np.array([0.6, 0.6, 0.6]), 'specular': np.array([1, 1, 1]), 'shininess': 100 }

Отражение

Сейчас мы рендерим лучи, которые выходят из источника света, ударяются о поверхность объекта и отражаются в камеру. Но что, если луч попадет в несколько объектов, прежде чем попасть в камеру? Появится отражение.

Каждый объект имеет коэффициент отражения в диапазоне от 0 до 1. Здесь 0 означает, что объект матовый, 1 — что объект зеркальный. Добавим свойство отражения ко всем сферам:

{ 'center': np.array([-0.2, 0, -1]), ..., 'reflection': 0.5 }
{ 'center': np.array([0.1, -0.3, 0]), ..., 'reflection': 0.5 }
{ 'center': np.array([-0.3, 0, 0]), ..., 'reflection': 0.5 }
{ 'center': np.array([0, -9000, 0]), ..., 'reflection': 0.5 }

Алгоритм

Чтобы включить вычисление отражений, нужно отследить отраженный луч после того, как произошло пересечение, и учесть цветовой вклад каждой точки этого пересечения. Повторяем этот процесс несколько раз.

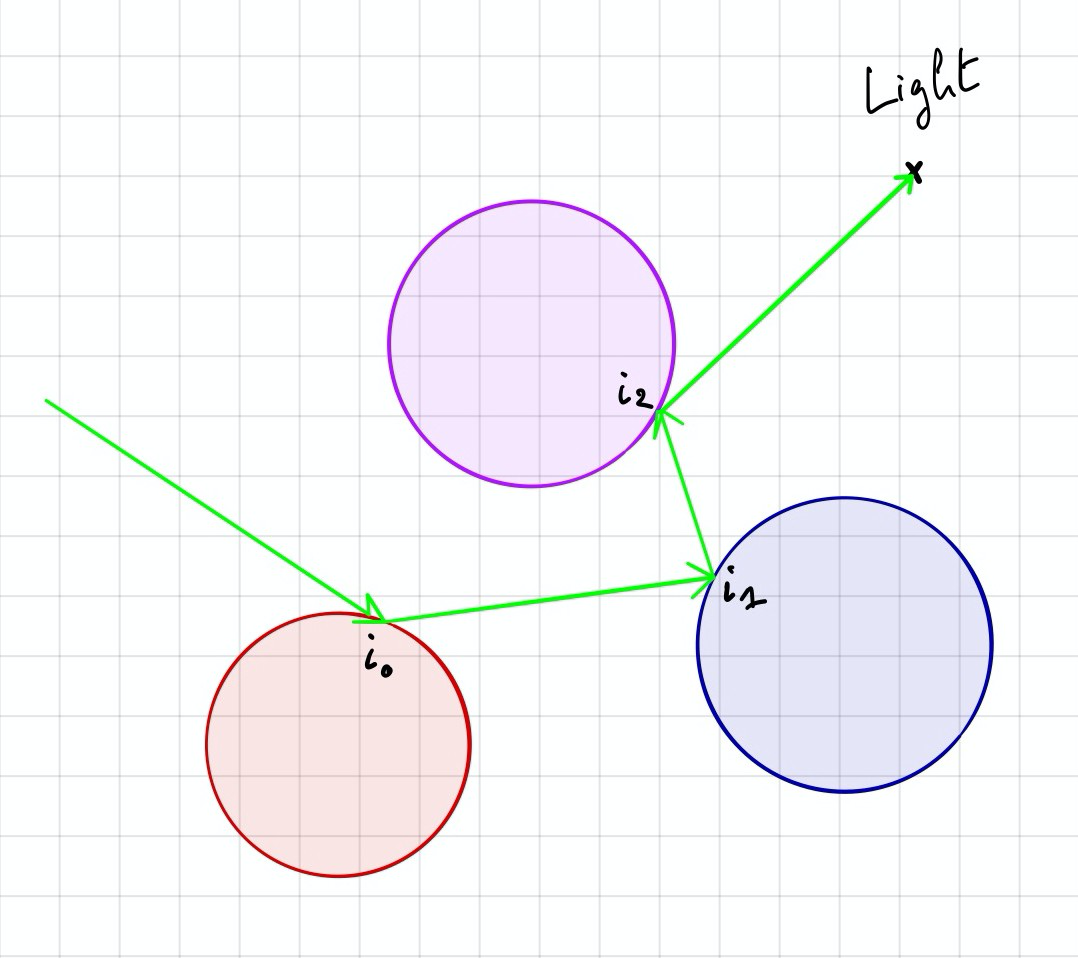
Рисунок 9
Рисунок 9

Расчет цвета

Чтобы получить цвет пикселя, нужно просуммировать вклад каждой точки пересечения луча:

где

  • c — конечный цвет пикселя;

  • i — освещенность, рассчитанная по модели Блинна-Фонга для точки пересечения;

  • r — отражение от пересекаемого объекта.

Когда прекратить вычисление этой суммы (и отслеживание отраженных лучей, соответственно), решаете вы сами.

Отраженный луч

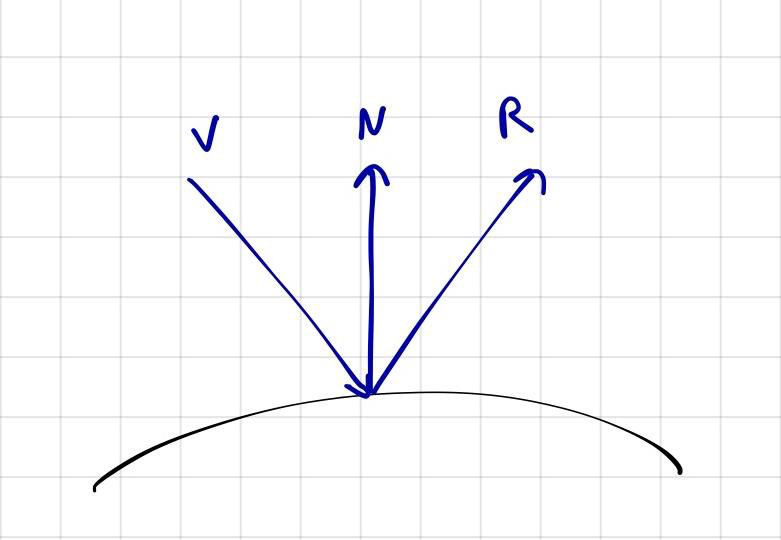
Прежде чем мы сможем все это записать в виде кода, нам нужно определить направление отраженного луча. Можно вычислить его следующим образом:

где

  • R — нормализованный отраженный луч;

  • L — единичный вектор направления отражаемого луча;

  • N — единичный вектор направления нормали к поверхности хода луча.

Рисунок 10
Рисунок 10

Добавим этот метод в начало кода вместе с функцией normalize():

def reflected(vector, axis):
   return vector — 2 * np.dot(vector, axis) * axis

Код

Посмотреть код
# глобальные переменные
max_depth = 3

# нужные данные для цикла

color = np.zeros((3))
reflection = 1

for k in range(max_depth):
   nearest_object, min_distance = # ...

   # ...
   illumination += # ...

   # отражение
   color += reflection * illumination
   reflection *= nearest_object['reflection']

   # начальная точка и направление нового луча
   origin = shifted_point
   direction = reflected(direction, normal_to_surface)
image[i, j] = np.clip(color, 0, 1)

Важно: теперь, когда мы поместили пересечения в другой цикл для отражений, нужно добавить операторы break во избежание бесполезных вычислений.

Вот и все. Запускаем код и наблюдаем результат:

Рисунок 11
Рисунок 11

Окончательный код

Итоговый код состоит из всего порядка сотни строк:

Посмотреть код
import numpy as np
import matplotlib.pyplot as plt

def normalize(vector):
    return vector / np.linalg.norm(vector)

def reflected(vector, axis):
    return vector - 2 * np.dot(vector, axis) * axis


def sphere_intersect(center, radius, ray_origin, ray_direction):
    b = 2 * np.dot(ray_direction, ray_origin - center)
    c = np.linalg.norm(ray_origin - center) ** 2 - radius ** 2
    delta = b ** 2 - 4 * c
    if delta > 0:
        t1 = (-b + np.sqrt(delta)) / 2
        t2 = (-b - np.sqrt(delta)) / 2
        if t1 > 0 and t2 > 0:
            return min(t1, t2)
    return None

def nearest_intersected_object(objects, ray_origin, ray_direction):
    distances = [sphere_intersect(obj['center'], obj['radius'], ray_origin, ray_direction) for obj in objects]
    nearest_object = None
    min_distance = np.inf
    for index, distance in enumerate(distances):
        if distance and distance < min_distance:
            min_distance = distance
            nearest_object = objects[index]
    return nearest_object, min_distance

width = 300
height = 200
max_depth = 3

camera = np.array([0, 0, 1])
ratio = float(width) / height
screen = (-1, 1 / ratio, 1, -1 / ratio) # left, top, right, bottom

light = { 'position': np.array([5, 5, 5]), 'ambient': np.array([1, 1, 1]), 'diffuse': np.array([1, 1, 1]), 'specular': np.array([1, 1, 1]) }

objects = [
    { 'center': np.array([-0.2, 0, -1]), 'radius': 0.7, 'ambient': np.array([0.1, 0, 0]), 'diffuse': np.array([0.7, 0, 0]), 'specular': np.array([1, 1, 1]), 'shininess': 100, 'reflection': 0.5 },
    { 'center': np.array([0.1, -0.3, 0]), 'radius': 0.1, 'ambient': np.array([0.1, 0, 0.1]), 'diffuse': np.array([0.7, 0, 0.7]), 'specular': np.array([1, 1, 1]), 'shininess': 100, 'reflection': 0.5 },
    { 'center': np.array([-0.3, 0, 0]), 'radius': 0.15, 'ambient': np.array([0, 0.1, 0]), 'diffuse': np.array([0, 0.6, 0]), 'specular': np.array([1, 1, 1]), 'shininess': 100, 'reflection': 0.5 },
    { 'center': np.array([0, -9000, 0]), 'radius': 9000 - 0.7, 'ambient': np.array([0.1, 0.1, 0.1]), 'diffuse': np.array([0.6, 0.6, 0.6]), 'specular': np.array([1, 1, 1]), 'shininess': 100, 'reflection': 0.5 }
]

image = np.zeros((height, width, 3))
for i, y in enumerate(np.linspace(screen[1], screen[3], height)):
    for j, x in enumerate(np.linspace(screen[0], screen[2], width)):

        # экран в начальной точке

        pixel = np.array([x, y, 0])
        origin = camera
        direction = normalize(pixel - origin)

        color = np.zeros((3))
        reflection = 1

        for k in range(max_depth):

            # проверка пересечений

            nearest_object, min_distance = nearest_intersected_object(objects, origin, direction)
            if nearest_object is None:

                break

            intersection = origin + min_distance * direction
            normal_to_surface = normalize(intersection - nearest_object['center'])
            shifted_point = intersection + 1e-5 * normal_to_surface
            intersection_to_light = normalize(light['position'] - shifted_point)

            _, min_distance = nearest_intersected_object(objects, shifted_point, intersection_to_light)

            intersection_to_light_distance = np.linalg.norm(light['position'] - intersection)
            is_shadowed = min_distance < intersection_to_light_distance

            if is_shadowed:
                break

            illumination = np.zeros((3))

            # ambiant

            illumination += nearest_object['ambient'] * light['ambient']

            # diffuse

            illumination += nearest_object['diffuse'] * light['diffuse'] * np.dot(intersection_to_light, normal_to_surface)

            # specular

            intersection_to_camera = normalize(camera - intersection)
            H = normalize(intersection_to_light + intersection_to_camera)
            illumination += nearest_object['specular'] * light['specular'] * np.dot(normal_to_surface, H) ** (nearest_object['shininess'] / 4)

            # reflection

            color += reflection * illumination
            reflection *= nearest_object['reflection']
            origin = shifted_point
            direction = reflected(direction, normal_to_surface)
        image[i, j] = np.clip(color, 0, 1)
    print("%d/%d" % (i + 1, height))
plt.imsave('image.png', image)

Что дальше ?

Это очень упрощенная программа, предназначенная для ознакомления с основами трассировки лучей. Есть много способов улучшить ее и реализовать другие функции. Например:

  • Можно создать классы и выяснить, что является специфическим для сфер, а что нет, определить базовый класс и реализовать другие объекты, такие как плоскости или треугольники;

  • То же самое и со светом. Добавить сюда POO и сделать так, чтобы можно было добавить несколько источников света в сцену;

  • Отделить свойства материала от геометрических свойств, чтобы иметь возможность применять один материал (например, синий матовый) к любому типу объектов;

  • Найти способ правильно расположить экран при любом положении и направлении камеры;

  • Смоделировать свет по-другому. В настоящее время это одна точка, поэтому тени от объектов «жесткие» или четко очерченные. Чтобы получить «мягкие» тени , нужно смоделировать источник света как 2D- или 3D-объект: диск или сферу.

Бонус

Ниже приведена анимация трассировки лучей. По сути это просто несколько раз отрендеренная сцена с камерой в разных положениях:

Код написан на Kotlin (можно оценить, насколько медленный по сравнению с ним Python) и доступен на GitHub.