На Хабре часто выкладывают туториалы по разным областям знаний. Сегодня, к старту нового потока курса по machine learning, поделимся с вами туториалом.... по ядерной физике, работе реакторов и прогнозной аналитике с использованием Python.

По данным Комиссии по ядерному регулированию, в США находится 31 исследовательский ядерный реактор. У автора есть лицензия на эксплуатацию одного из них, и в этой статье он продемонстрирует, как применил методы машинного обучения и общего анализа данных для прогнозирования уровней мощности импульсов и повышения показателя воспроизводимости наших экспериментов.

Предпосылки

Реактор ядерного распада работает на энергии расщепления атомов. Когда уран-235 поглощает нейтрон, появляется шанс расщепления и распада, высвобождаются продукты деления, нейтроны и кинетическая энергия. Эта энергия нагревает теплоноситель, который обычно подаётся в теплообменник, а затем в вырабатывающую электричество паровую турбину. На моем объекте находится реактор TRIGA, который не производит никакого электричества — он используется исключительно для исследований и экспериментов.

Забавный факт: один килограмм Урана-235 содержит примерно в 3 миллиона раз больше энергии, чем один килограмм угля. Ах да, реакция деления не приводит к выбросам углерода. (Я вовсе не предвзят.)

В сравнении с коммерческим реактором TRIGA уникален во многих отношениях, например, он может выполнять “импульс”. Большой отрицательный коэффициент реактивности топлива означает, что с повышением температуры реактивность — и, следовательно, скорость цепных реакций деления — уменьшается. Это означает, что реактор ограничивает сам себя в смысле уровня мощности и, благодаря идее топлива, после импульса отключается физически без участия оператора. Вот почему они позволяют таким людям, как я, им управлять!

Импульс работает путём пневматического (с использованием сжатого воздуха) выталкивания одного из стержней управления из активной зоны реактора, что вызывает быстрое увеличение уровня мощности. Следующие события происходит за нескольких миллисекунд:

• Стержень управления выдвигается из сердечника вертикально вверх.

• Уровень мощности увеличивается примерно с 50 Вт до 2000 МВт.

• При таком высоком уровне мощности быстрый эффект отрицательной обратной связи топлива обеспечивает отрицательную реактивность активной зоны, которая отключается.

В этот момент стержень управления всё ещё может находиться на пути из ядра, но впоследствии из-за силы тяжести упадёт обратно. В итоге вы получаете функцию отклика мощности P(t), которая выглядит, примерно как показано на втором рисунке — по мере выталкивания управляющего стержня мощность увеличивается, а затем быстро уменьшается с добавлением отрицательной реактивности.

Хотя пульсация имеет множество исследовательских применений, она особенно хорошо работает в имитации испускаемого ядерным взрывом сильного излучения.

В частности, мы наблюдаем, как на атомном уровне нейтроны и гамма-лучи взаимодействуют с электроникой. Допустим, вы разрабатываете новый электронный компонент, который будет использоваться, чтобы работать в некоей части системы ядерного оружия.

• Насколько вы уверены, что в близости от ядерного взрыва ваша электроника выживет?

• Какие повреждения имеет интегральная схема, 10 лет простоявшая рядом с радиоактивной боеголовкой? Как это повреждение повлияет на функциональность вашего компонента?

• Или что, если вы разрабатываете процессор,который будет работать в новом истребителе.

• Может ли включённая вашим процессором система управления полётом при воздействии определённого количества радиации выйти из строя?

Понятна серьёзность этих вопросов. Соедините это с тем фактом, что истинная ядерная детонация — своего рода испытание и она имеет ряд проблем (не говоря уже о том, что она запрещена Договором о всеобъемлющем запрещении ядерных испытаний), и вы скоро согласитесь, что импульс реактора — это его ключевая характеристика.

Стоит пояснить, что этот импульс генерирует только излучение. В эксперимента такого типа ничего не взрывается. Мы просто подвергаем образец высокому уровню радиации в чрезвычайно контролируемой и предназначенной для этой задачи среде.

Максимальный достигаемый импульсом уровень мощности исходя из “стоимости” реактивности стержней управления может выбрать оператор. Для многих ядерных реакторов эта стоимость измеряется в долларах, и поскольку это выходит за рамки данной статьи, чтобы объяснить, почему мы используем этот, казалось бы, странный блок, вы можете прочитать все об этом здесь, если хотите.

В зависимости от эксперимента может потребоваться определённый уровень импульсной мощности. Положение стержней управления в сердечнике определяет уровень мощности в любой момент времени. Собранный из данных моей работы на реакторе набор состоит из этих значений, а также нескольких других, которые описываются ниже:

• Дата. Конкретная дата в формате datetime, когда произошёл импульс.

• Расчётная реактивность. Оценочная импульса реактивности в долларах. Эта оценка определяется обращением к объединённой стоимости определённого стержня управления. Пример: экспериментатор запрашивает импульс стоимостью $2,00. Оператор найдёт позицию для контрольного стержня на основе общей стоимости.

• Позиции стержня. В сердечнике находятся четыре управляющих стержня — переходный, шайба 1, шайба 2 и управляющий стержень. Метки "Trans, S1, S2, Reg" в моем наборе — это связанные с физическим расположением управляющих стержней в ядре значения. Они варьируются от 0 до 960, где 0 — это полностью вставленный сердечник, а 960 – полностью удалённый.

• Пиковая мощность. Измерения в мегаваттах.

• Общая энергия Измеряется в мегаваттах-секундах.

• Пиковая температура. Измеряется в градусах Цельсия: это пиковая температура, достигаемая в измерительном топливном элементе (IFE). Чтобы контролировать температуру сердечника, внутри нескольких топливных стержней встроены термопары.

• Расчетная реактивность. Это "истинное" значение реактивности, обычно оно на определенную величину отличается от расчётной. Оно автоматически рассчитывается консолью реактора.

В оставшейся части статьи я проанализирую набор данных, чтобы понять, какие возможны инсайты. Кроме того, чтобы прогнозировать расчётную реактивность на основе предполагаемой реактивности и положений стержней, я применю модель машинного обучения — линейную регрессию. Эта модель поможет нам быть точнее с нашими импульсами (в определённой степени — больше размышлений об этом позже), также модель повысит эффективность и достоверность экспериментов. Моя конечная цель — сделать наши импульсы более точными и повторяемыми с точки зрения полученного конкретным образцом количества облучения.

Исследовательский анализ данных (EDA)

Я очистил данные заранее, избавлю вас от этих деталей. В большинстве случаев очистка набора данных – это удаление ошибочных или неполных записей. Было много ошибок ручного ввода (опечаток), которые я должен был обнаружить и исправить, не хватало точек данных, их я либо полностью удалил, либо заменил средними значениями.

Как только у меня будут чистые данные, первое, что я сделаю, — импортирую соответствующие библиотеки и загружу свой фрейм данных:

import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import numpy as npfrom sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn import metrics
from sklearn.metrics import r2_scoredf = pd.read_excel('Pulse_Data_2021_NO_NULL.xlsx', )

После этого я всегда использую три основные функции, чтобы изучить общие характеристики моих данных — .head(), .info() и .describe().

.head() просто показывает несколько верхних строк фрейма данных, так можно увидеть, как данные структурированы в целом:

.info() выводит количество записей во фрейме, имена столбцов, количество нулевых записей в каждом столбце и тип данных для каждого столбца:

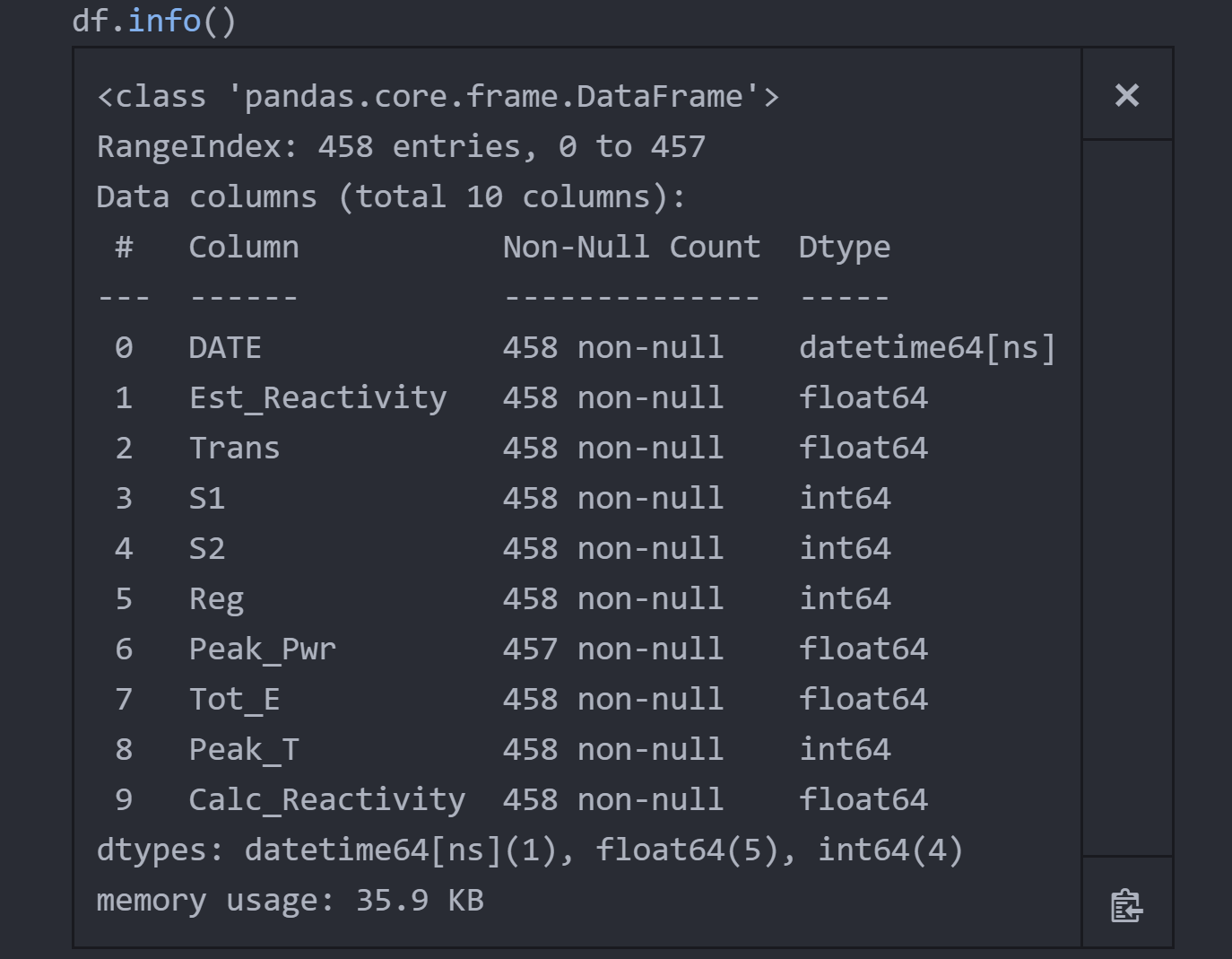
И .describe() предоставляет некоторый сводный анализ самих данных — среднее значение, стандартное отклонение, квартили и так далее от каждого столбца. Мне нравиться транспонировать столбец, чтобы удобно читать его:

Следующий шаг моего EDA – просто начать строить графики того, что может иметь смысл. Например, я подумал, что было бы интересно увидеть связь между расчётной реактивностью и пиковой мощностью, поэтому сделал простую диаграмму рассеяния:

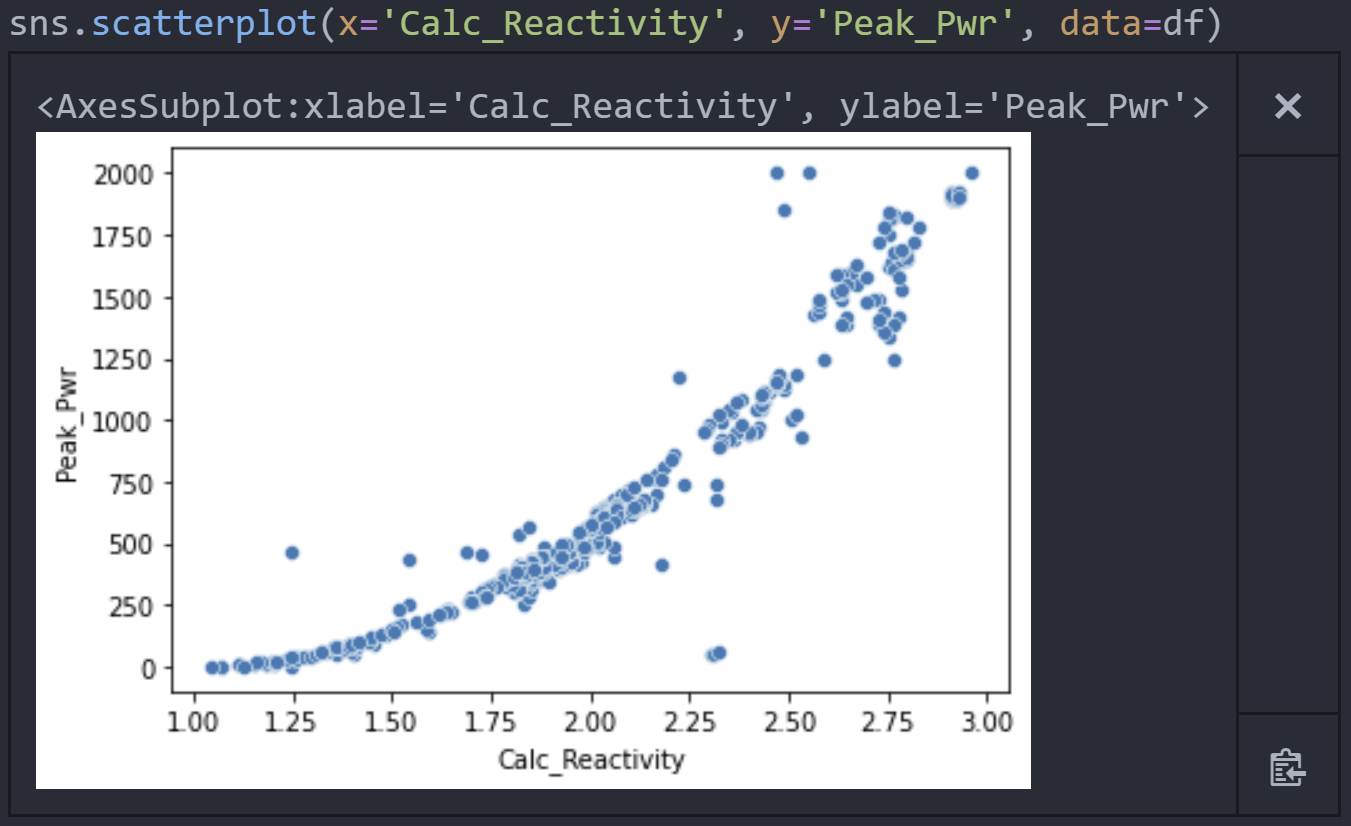
Между двумя переменными существует четкая экспоненциальная зависимость, она согласуется с принципами управляющей этой реакцией реакторной кинетики. График также полезен тем, что выявляет потенциальные точки выброса — либо странное поведение реактора, либо, что более вероятно, ошибочные записи. Из этого графика я нашел дополнительные записи с опечатками, которые нужно было исправить или убрать.

Корреляционная тепловая карта — это ещё один полезный инструмент, который может применяться к большинству числовых наборов данных. На рисунке 7 ниже показано, какие столбцы со значениями в диапазоне от -1 до 1 тесно коррелируют друг с другом.

Я пытаюсь сделать прогнозы предполагаемой реактивности точнее, мой следующий шаг — сравнить его распределение с расчётной реактивностью. Для этого я накладываю две гистограммы и придаю им приятный вид:

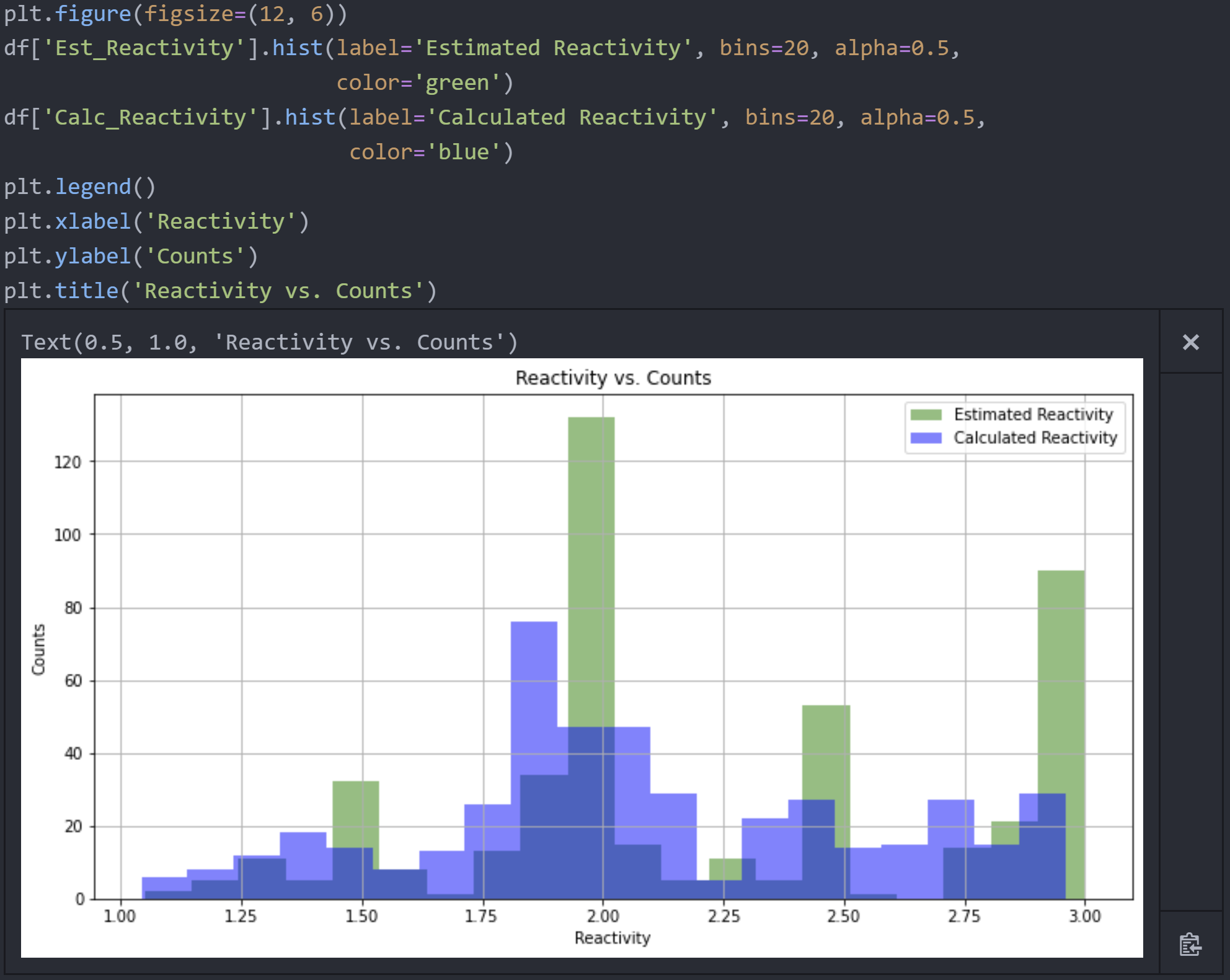
Существуют дискретные значения импульсной реактивности, которые мы обычно используем, когда решаем, насколько “большой” импульс мы хотим. Рисунок 8 наглядно отражает это, показывая, что 1.50, 2.00, 2.50 и 3.00 – это общие оценочные значения. Можно было бы ожидать нормального распределения расчётных значений реактивности вокруг каждого из её расчётных значений, что показано (хотя и слабо) синим графиком.

Если ещё раз взглянуть на рис. 8, оказывается, что оценочная реактивность несколько выше рассчитанной. Это означает, что, вообще говоря, если вы запросите импульс стоимостью в $2,00, вы на самом деле получите реактивность немного меньше. Я могу количественно оценить его: нужно вычесть один столбец из другого и найти среднее значение:

Выше показано, что в среднем “истинная”, рассчитанная реактивность на 16 центов дешевле расчётной реактивности.

Наконец, я сгенерировал график, который служит интересным представлением работы реактора во времени. Этот реактор впервые запустили (то есть “вывели в критичесоке состояние”) в 1992 году, и график количества импульсов в год с тех пор показывает несколько периодов сильно сниженной активности:

Глядя на рисунок 10, вы можете задаться вопросами:

• Почему в 1994-1996 годах и в 2013-2014 годах импульсов было так мало?

• Были ли повлиявшие на тип экспериментов на объекте административные изменения, которые повлияли на тип экспериментов на этом объекте?

• Были ли какие-либо новые национальные или университетские исследовательские разработки, требующие дополнительных импульсов?

• Какие эксперименты проводились в 2000 и 2020-2021 годах (сейчас), которые требовали столько импульсов, и почему в этот период не было таких экспериментов?

Удивительно, как много инсайтов можно получить из нескольких маленьких графиков.

Прогнозное моделирование

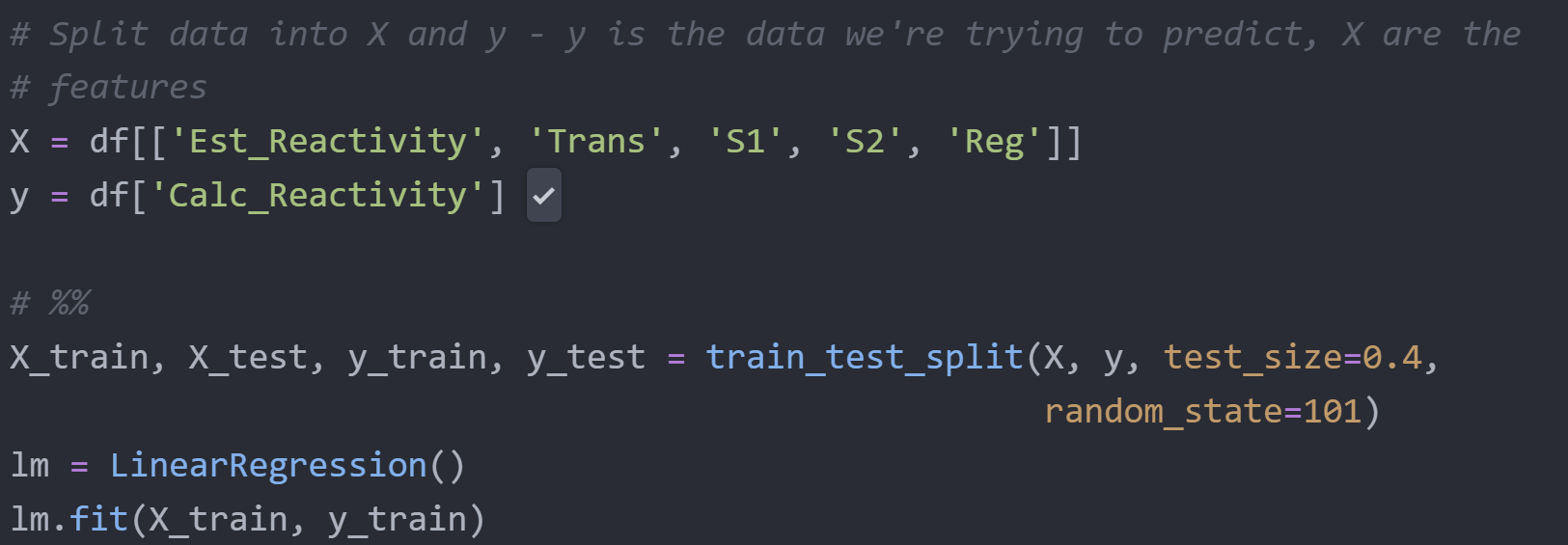
Задача прогнозирования расчётной реактивности подходит для модели линейной регрессии. Это считается моделью обучения с учителем, поскольку данные уже помечены (дл обучения модели даны значения x и y). Технически это модель множественной регрессии (определение которой включает в себя линейную регрессию), потому что она использует несколько независимых переменных (Est_Reactivity, Trans, S1, S2, Reg), чтобы спрогнозировать значение зависимой переменной (Calc_Reactivity).

Сначала я разбил данные на обучающий и тестовый наборы, чтобы дать модели объективную оценку. Затем я инстанцирую модель и обучаю её на данных:

Как только модель обучена, чтобы сравнить выводы модели с ожидаемыми значениями, я использую данные для тестирования. Абсолютно прямая линия означала бы идеальную модель:

С несколькими заметными отклонениями, модель делает большую работу по точному прогнозированию. В зависимости от того, для чего применяется модель, возможно, стоит изучить данные ещё глубже, чтобы определить, откуда исходят эти отклонения и как их можно смягчить, чтобы повысить точность модели. В моем случае этой модели достаточно. Я даже могу количественно оценить качество обучения, вычислив для моей модели значение коэффициента детерминации:

Коэффициент детерминации — это доля дисперсии в зависимой переменной, которая прогнозируема исходя из независимой переменной. Выраженный в процентах, 91% дисперсии в оценочной реактивности любого данного импульса можно объяснить с помощью наших входных значений. Вывод: это отличная модель для наших целей. Тем не менее, есть ещё одна проверка, которую я могу сделать, чтобы больше узнать о модели.

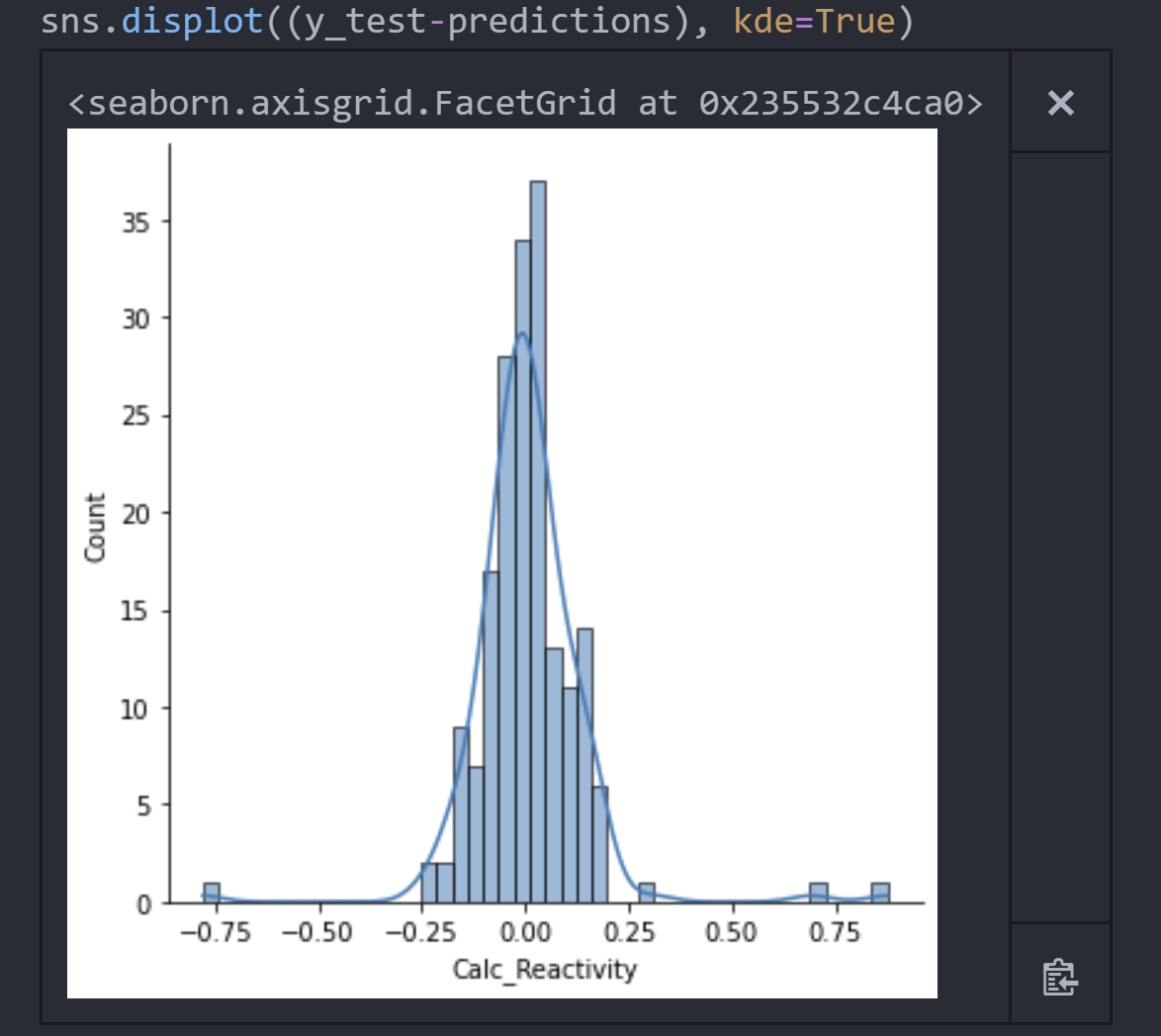
Рисунок 14 — это гистограмма остатков, или расстояние между любой заданной точкой данных и линией наиболее подходящей регрессии. График показывает, что нормальное распределение случайной ошибки — около нуля. Это хорошо. Если бы это было не так, то у нас могли возникнуть проблемы с нашей моделью и/или набором данных. Опять же, есть заметные отклонения, но не о чем беспокоиться, когда мы подкреплены впечатляющей дисперсией зависимой переменной.

Выводы (и ограничения)

С помощью этой модели теперь я могу точно предсказать значение импульсной реактивности, основываясь на таких параметрах реактора, как положение управляющих стержней и импульс в долларах. Ясность важна во всех экспериментах, и эта модель поможет подтянуть значения импульсов и обеспечить одинаковое облучение радиацией для каждого облучаемого компонента.

Примечание. Модель имеет ряд ограничений, которые могут быть очевидны для тех, у кого есть знания о кинетике реактора и о его работе. А именно, модель не знает о предыдущих операциях и чрезвычайно важном накоплении продуктов распада. Ксенон-135 образуется (и сгорает) с течением времени по мере работы реактора, существенно влияя на поглощение нейтронов и поведение реактора.

Хотите научиться использовать машинное обучение как и автор статьи — можете обратить внимание на наш курс по Machine Learning, или на его расширенную версию, в которой рассматривается и глубокое обучение — "Machine Learning и Deep Learning".

Узнайте, как прокачаться и в других специальностях или освоить их с нуля:

• Профессия Data Scientist

• Профессия Data Analyst

• Курс по Data Engineering