Линейный поиск — это алгоритм оптимизации, который может использоваться для целевых функций с одной или несколькими переменными. Он предоставляет возможность использовать алгоритм одномерной оптимизации, например поиск методом деления пополам (бисекции) для многомерной целевой функции, работая с линейным поиском для определения оптимального размера шага в каждом измерении от известной точки до оптимума. Мы уже делились переводами Джейсона Браунли, например статьёй о смешанных ансамблях, а в этом учебном руководстве, которое мы перевели к старту курса о машинном и глубоком обучении, рассказывается об основах: вы узнаете, как на Python с помощью линейного поиска выполнить оптимизацию.

Прочитав это руководство, вы узнаете:

• что линейный поиск — это алгоритм оптимизации для одномерных и многомерных задач оптимизации;

• что библиотека SciPy предоставляет API выполнения линейного поиска, который требует знания о том, как вычисляется первая производная вашей целевой функции;

• как выполнить линейный поиск для целевой функции и работать с результатом.

Давайте начнём.

Обзор

Этот учебный материал разделён на три части:

1. Что такое линейный поиск?

2. Линейный поиск на Python.

3. Как выполняется линейный поиск? Он состоит из:

a) определения целевой функции;

б) выполнения линейного поиска;

в) работы со сбоями алгоритма.

Что такое линейный поиск?

Линейный поиск — это алгоритм оптимизации для одномерной или многомерной оптимизации. Он требует начальной позиции в пространстве поиска, а также указания направления поиска. Затем он из начальной выбирает следующую позицию в пространстве поиска, которая приведёт к значению лучше или же к наилучшему значению целевой функции.

Направление имеет знак (плюс или минус) вдоль линии и максимальную протяжённость поиска, поэтому его лучше рассматривать как область поиска кандидатов, оно должно быть достаточно большим, чтобы охватить оптимумы или точку лучше начальной.

Линейный поиск автоматически выберет коэффициент масштаба, который называется альфа, для размера шага (направления) исходя из текущей, минимизирующей целевую функцию позиции. Чтобы найти оптимальную точку в выбранном направлении и выбрать соответствующую альфа, используется другой алгоритм одномерной оптимизации

Один из подходов заключается в применении линейного поиска, выбирающего коэффициент шага, который минимизирует одномерную функцию [...]. Мы можем применить метод одномерной оптимизации по нашему выбору.

— Алгоритмы оптимизации, 2019. — С. 54.

Альфа — коэффициент масштаба для направления, поэтому при поиске учитываются только значения в диапазоне от 0,0 до 1,0. Один шаг линейного поиска решает задачу минимизации, которая минимизирует целевую функцию для текущей позиции в сумме с масштабируемым направлением, то есть:

• Минимизирует objective(position + alpha * direction).

Таким образом, линейный поиск работает в одном измерении за один раз и возвращает расстояние перемещения в выбранном направлении.

Каждая итерация метода линейного поиска вычисляет направление поиска pk, а затем решает, как далеко двигаться в этом направлении.

— Численная оптимизация, 2006. — С. 30. 

Чтобы перенести пространство поиска к решению, линейный поиск может быть вызван повторно и может завершиться неудачей, если выбранное направление не содержит точки с меньшим значением целевой функции, например когда алгоритм направлен искать по склону вверх.

Решение приблизительно или неточно и в зависимости от формы пространства поиска может не оказаться общим решением. Условия, при которых этот алгоритм подходит, называются условиями Вольфе. Теперь, когда мы знакомы с линейным поиском, давайте посмотрим, как выполнять его на Python.

Линейный поиск на Python

Выполнить линейный поиск на Python можно вручную, с помощью функции line_search(). Она поддерживает одномерную оптимизацию, а также многомерные задачи оптимизации. Эта функция принимает имя целевой функции и имя градиента для целевой функции, а также текущее положение в пространстве поиска и направление движения.

Таким образом, вы должны знать первую производную вашей целевой функции. Вы также должны иметь некоторое представление о том, с чего начать поиск и насколько широко выполнять его. Напомним, что поиск может выполняться несколько раз с разными направлениями (знаком и протяжённостью).

...
result = line_search(objective, gradient, point, direction)

Функция возвращает кортеж из шести элементов, включая коэффициент масштаба для направления, называемый альфа, и количество выполненных вычислений функций, а также другие значения. Первый элемент в результирующем кортеже содержит альфа. Если поиск не сойдётся, альфа будет иметь значение None.

...
# retrieve the alpha value found as part of the line search
alpha = result[0]

Альфа, начальная точка и направление могут использоваться при построении конечной точки линейного поиска.

...
# construct the end point of a line search
end = point + alpha * direction

Для задач оптимизации с более чем одной входной переменной, например многомерной оптимизации, функция line_search() вернёт одно альфа-значение для всех измерений. Это значит, функция предполагает, что оптимум равноудалён от начальной точки во всех измерениях, такое ограничение существенно. Теперь, после ознакомления с тем, как в Python выполнять линейный поиск, давайте рассмотрим работающий пример.

Как выполняется линейный поиск?

Мы можем продемонстрировать, как использовать линейный поиск с простой одномерной целевой функцией и её производной. Этот раздел, в свою очередь, разделён на несколько частей, включая определение тестовой функции, выполнение линейного поиска и обработку неудачных случаев, когда оптимум не находится.

Определение целевой функции

Во-первых, мы можем определить целевую функцию. Здесь поработаем с одномерной целевой функцией, а именно со сдвинутой на небольшую величину от нуля функцией x^2. Это выпуклая функция, она была выбрана потому, что её легко понять, а также легко вычислить первую производную.

• objective(x) = (-5 + x)^2.

Обратите внимание, что линейный поиск не ограничивается одномерными или выпуклыми функциями. Реализация этой функции приведена ниже.

# objective function
def objective(x):
	return (-5.0 + x)**2.0

Первая производная этой функции может быть вычислена аналитически следующим образом:

• gradient(x) = 2 * (-5 + x).

Градиент для каждого входного значения просто указывает наклон к оптимумам в каждой точке. Реализация функции градиента приведена ниже:

# gradient for the objective function
def gradient(x):
	return 2.0 * (-5.0 + x)

Можно определить диапазон входных данных для x от -10 до 20 и вычислить целевое значение для каждого входного значения:

...
# define range
r_min, r_max = -10.0, 20.0
# prepare inputs
inputs = arange(r_min, r_max, 0.1)
# compute targets
targets = [objective(x) for x in inputs]

Затем, чтобы получить представление о форме функции, мы можем построить график входных значений в сравнении с целевыми значениями:

...
# plot inputs vs objective
pyplot.plot(inputs, targets, '-', label='objective')
pyplot.legend()
pyplot.show()

Связав всё это воедино, получим такой код:

# plot a convex objective function
from numpy import arange
from matplotlib import pyplot
 
# objective function
def objective(x):
	return (-5.0 + x)**2.0
 
# gradient for the objective function
def gradient(x):
	return 2.0 * (-5.0 + x)
 
# define range
r_min, r_max = -10.0, 20.0
# prepare inputs
inputs = arange(r_min, r_max, 0.1)
# compute targets
targets = [objective(x) for x in inputs]
# plot inputs vs objective
pyplot.plot(inputs, targets, '-', label='objective')
pyplot.legend()
pyplot.show()

Программа вычисляет входные значения (x) в диапазоне от -10 до 20 и создаёт график, показывающий знакомую U-образную форму параболы. Оптимум функции, по-видимому, находится в точке x=5,0, целевое значение — 0,0.

Выполнение линейного поиска

Затем можно выполнить линейный поиск по этой функции. Во-первых, мы должны определить отправную точку поиска и его направление. Здесь воспользуемся начальной точкой x=-5, расстояние от которой до оптимума — около 10 единиц. Сделаем большой шаг вправо, в данном случае в 100 единиц (что значительно превышает оптимум), например, в положительном направлении. Напомним, что направление похоже на размер шага и поиск масштабирует размер шага, чтобы найти оптимум:

...
# define the starting point
point = -5.0
# define the direction to move
direction = 100.0
# print the initial conditions
print('start=%.1f, direction=%.1f' % (point, direction))
# perform the line search
result = line_search(objective, gradient, point, direction)

Затем поиск ищет оптимумы и возвращает альфа или расстояние, чтобы изменить направление. Из результата мы можем получить значение альфа, а также количество выполненных вычислений функций:

...
# summarize the result
alpha = result[0]
print('Alpha: %.3f' % alpha)
print('Function evaluations: %d' % result[1])

Мы можем использовать альфа вместе с нашей начальной точкой и размером шага для вычисления местоположения оптимумов и вычисления целевой функции в этой точке (которая, как мы ожидаем, будет равна 0,0):

...
# define objective function minima 
end = point + alpha * direction
# evaluate objective function minima
print('f(end) = %.3f' % objective(end))

Затем, для развлечения, мы можем снова построить график функции и показать начальную точку в виде зелёного квадрата, а конечную точку — в виде красного квадрата.

...
# define range
r_min, r_max = -10.0, 20.0
# prepare inputs
inputs = arange(r_min, r_max, 0.1)
# compute targets
targets = [objective(x) for x in inputs]
# plot inputs vs objective
pyplot.plot(inputs, targets, '--', label='objective')
# plot start and end of the search
pyplot.plot([point], [objective(point)], 's', color='g')
pyplot.plot([end], [objective(end)], 's', color='r')
pyplot.legend()
pyplot.show()

Ниже приведён полный пример выполнения линейного поиска для выпуклой целевой функции:

# perform a line search on a convex objective function
from numpy import arange
from scipy.optimize import line_search
from matplotlib import pyplot
 
# objective function
def objective(x):
	return (-5.0 + x)**2.0
 
# gradient for the objective function
def gradient(x):
	return 2.0 * (-5.0 + x)
 
# define the starting point
point = -5.0
# define the direction to move
direction = 100.0
# print the initial conditions
print('start=%.1f, direction=%.1f' % (point, direction))
# perform the line search
result = line_search(objective, gradient, point, direction)
# summarize the result
alpha = result[0]
print('Alpha: %.3f' % alpha)
print('Function evaluations: %d' % result[1])
# define objective function minima
end = point + alpha * direction
# evaluate objective function minima
print('f(end) = f(%.3f) = %.3f' % (end, objective(end)))
# define range
r_min, r_max = -10.0, 20.0
# prepare inputs
inputs = arange(r_min, r_max, 0.1)
# compute targets
targets = [objective(x) for x in inputs]
# plot inputs vs objective
pyplot.plot(inputs, targets, '--', label='objective')
# plot start and end of the search
pyplot.plot([point], [objective(point)], 's', color='g')
pyplot.plot([end], [objective(end)], 's', color='r')
pyplot.legend()
pyplot.show()

Программа-пример сначала сообщает начальную точку и направление. Поиск выполняется, и обнаруживается изменяющая направление для нахождения оптимума значение альфа, в данном случае — найденное после трёх вычислений функции 0.1. Точка оптимума находится на отметке 5,0, значение y, как и ожидалось, равно 0,0:

start=-5.0, direction=100.0
Alpha: 0.100
Function evaluations: 3
f(end) = f(5.000) = 0.000

Наконец, создаётся график функции, показывающий зелёную начальную точку и красную цель.

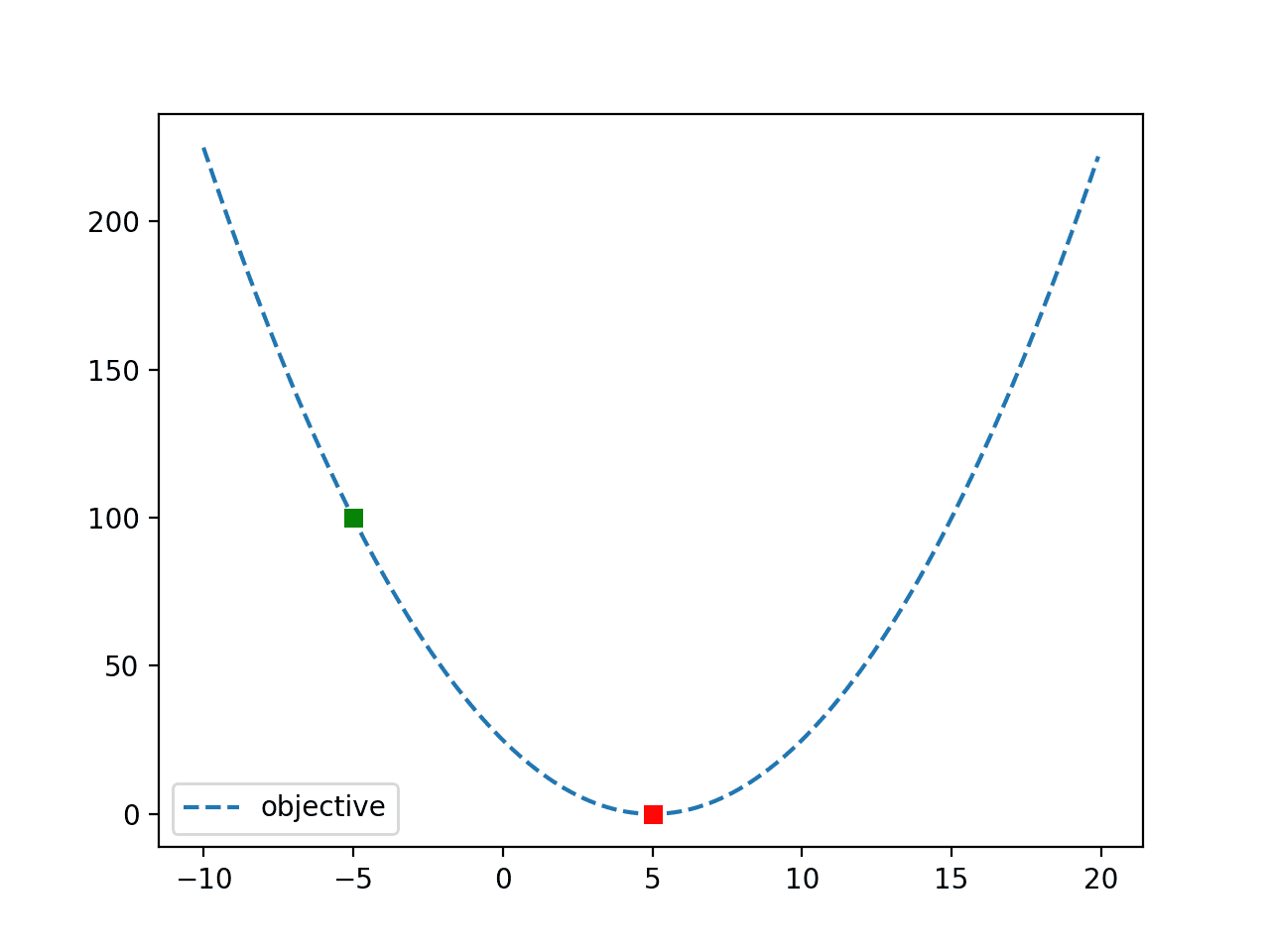
Работа со сбоями алгоритма

Линейный поиск не гарантирует нахождения оптимумов функции. Он может не найти оптимумы, если задано значение направления, недостаточно большое, чтобы охватить их. Например, найти оптимумы будет невозможно, когда направление имеет значение 3. Продемонстрировать это можно на полном примере ниже:

# perform a line search on a convex objective function with a direction that is too small
from numpy import arange
from scipy.optimize import line_search
from matplotlib import pyplot
 
# objective function
def objective(x):
	return (-5.0 + x)**2.0
 
# gradient for the objective function
def gradient(x):
	return 2.0 * (-5.0 + x)
 
# define the starting point
point = -5.0
# define the direction to move
direction = 3.0
# print the initial conditions
print('start=%.1f, direction=%.1f' % (point, direction))
# perform the line search
result = line_search(objective, gradient, point, direction)
# summarize the result
alpha = result[0]
print('Alpha: %.3f' % alpha)
# define objective function minima
end = point + alpha * direction
# evaluate objective function minima
print('f(end) = f(%.3f) = %.3f' % (end, objective(end)))

При выполнении примера поиск достигает предела альфа 1,0, что даёт конечную точку от -2 до 49. При f(5) = 0,0 от оптимумов очень далеко:

start=-5.0, direction=3.0
Alpha: 1.000
f(end) = f(-2.000) = 49.000

Кроме того, мы можем выбрать неправильное направление, ведущее только к вычислениям хуже стартовой точки. Здесь оно будет отрицательным в сторону от оптимума, например, вверх по склону от начальной точки:

...
# define the starting point
point = -5.0
# define the direction to move
direction = -3.0

Ожидается, что поиск не сойдётся, поскольку он не может найти какие-либо точки лучше начальной. Полный пример поиска, который не сходится, приведён ниже:

# perform a line search on a convex objective function that does not converge
from numpy import arange
from scipy.optimize import line_search
from matplotlib import pyplot
 
# objective function
def objective(x):
	return (-5.0 + x)**2.0
 
# gradient for the objective function
def gradient(x):
	return 2.0 * (-5.0 + x)
 
# define the starting point
point = -5.0
# define the direction to move
direction = -3.0
# print the initial conditions
print('start=%.1f, direction=%.1f' % (point, direction))
# perform the line search
result = line_search(objective, gradient, point, direction)
# summarize the result
print('Alpha: %s' % result[0])

Выполнение программы приводит к предупреждению LineSearchWarning, указывающему на то, что поиск, как и ожидалось, не может сойтись. Альфа — возвращённое в результате поиска значение — равно None:

start=-5.0, direction=-3.0
LineSearchWarning: The line search algorithm did not converge
warn('The line search algorithm did not converge', LineSearchWarning)
Alpha: None

Дальнейшее чтение

Если вы хотите глубже погрузиться в тему, смотрите этот раздел.

Книги

• Алгоритмы оптимизации, 2019.

• Численная оптимизация, 2006.

API

• Оптимизация и поиск корней (scipy.optimize).

• Оптимизация (scipy.optimize).

• scipy.optimize.line_search API.

Статьи

• Линейный поиск. Википедия.

• Условия Вольфе. Википедия.

Резюме

Из этого руководства вы узнали, как выполнить оптимизацию линейного поиска на Python. В частности, вы узнали:

• что линейный поиск — это алгоритм оптимизации для одномерных и многомерных задач оптимизации;

• что библиотека SciPy предоставляет API выполнения линейного поиска, требующий знания о том, как вычисляется первая производная вашей целевой функции;

• как выполнить линейный поиск для целевой функции и работать с его результатом.

Применяемые в машинном обучении методы оптимизации, конечно же, не ограничиваются одним лишь линейным поиском, они многочисленны, разнообразны и у каждого есть свои недостатки и преимущества. Если вы хотите погрузиться в машинное обучение, изучить оптимизацию глубже, но не хотите ограничивать себя областью ML, вы можете обратить внимание на наш курс "Machine Learning и Deep Learning", партнёр которого, компания NVIDIA, не нуждается в представлении.

Узнайте, как прокачаться и в других специальностях или освоить их с нуля:

• Профессия Data Scientist

• Профессия Data Analyst

• Курс по Data Engineering