В предыдущих статьях Пространственные спектры и фрактальность рельефа, силы тяжести и снимков и Кто и как поломал Землю, или откуда возникли планетарные горные хребты и разломы рассказано, как образовалась фрактальная картина поверхности и силы тяжести нашей планеты в диапазоне масштабов от планетарного и до субметрового. Теперь мы обсудим различные методы выделения направлений для геологического линеаментного анализа. Если 3D модели мы строим, пользуясь кольцевым преобразованием Радона, то штрихи на растровых изображениях можно выделять линейным преобразованием Радона, также известным как линейное преобразование Хафа в методах компьютерного зрения. Именно эти базовые алгоритмы компьютерного зрения и послужили основой вычислительной геологии. Про кольцевое преобразование Радона смотрите подробнее в статье Методы компьютерного зрения для решения обратной задачи геофизики, а про линейное поговорим сегодня. Кроме того, мы обратим внимание и на современные векторные и графовые алгоритмы анализа.

Контурные розы диаграммы новейших тектонических линеаментов по результатам высокочастотной фильтрации глобальных моделей Gebco 2019 Bathymetry и Sandwell & Smith Gravity
Введение
Для начала разберемся с терминологией. Линеамент, по определению, является линейным проявлением (глубинных) геологических структур и традиционно выделяется экспертным методом — то есть вручную опытным геологом. При машинном же анализе получаемые результаты называют просто штрихами, пока не установлена их связь с геологическими объектами, иными словами, их геологическая значимость. В то время как определение штрихов это чисто техническая и хорошо изученная задача, не требующая никаких знаний в геологии, выбор из этих штрихов геологически значимых линеаментов является геологической задачей.
Технически выделение протяженных штрихов на растровых данных проблемы не представляет, сложность кроется в определении их связи с геологическими объектами. Линеаментный анализ может выполняться на самых разных растровых данных — начиная от глобальных моделей силы тяжести и рельефа разрешением порядка десятков километров и заканчивая сверхдетальными космическими и аэрофотоснимками разрешением в доли метра. В первом случае, для геофизических данных все выделяемые на них штрихи оказываются линеаментами, в предыдущей статье приведен соответствующий пример с картой тектонических плит и микроплит по данным высокочастотной фильтрации глобального поля силы тяжести. В последнем случае, для фотографий, очевидно, далеко не все изменения цвета имеют геологическую природу. При этом, зачастую один и тот же штриховой элемент может интерпретироваться и как линеамент и как помеха — например, если автомагистраль проложена согласно особенностям рельефа, то она совпадает с линеаментом, а иначе является техногенной помехой. Также и границы тени могут порождать ложные линеаменты, притом зависящие от угла съемки, а при вертикальной съемке в полдень совпадать с геологическими границами. Следовательно, выделение геологически значимых линеаментов очень усложняется при использовании оптических снимков и прочих данных, не являющихся геофизическими. К счастью, как мы уже говорили в предыдущих статьях, связь между линеаментами разных масштабов существует и хорошо изучена, так что, определив линеаменты на данных рельефа и поля силы тяжести низкого разрешения, можно найти их основные направления и использовать этот результат для асимметричной фильтрации снимков прежде операции выделения штрихов.
Практическая трудность определения и отображения значимых направлений известна не только геологам, например, с аналогичными трудностями сталкиваются метеорологи. Существуют и соответствующие методические пособия, предлагающие различные методы визуализации. Мы ограничимся использованием так называемых роз-диаграмм, которые показывают значения некоторого распределения для всех направлений (Пустовит, Попов, 2009). В предыдущей статье приведены розы-диаграммы планетарных линеаментов.
Зачастую, розы-диаграммы используются совместно с так называемыми линиями вытянутости (соответствующими направлениям минимального локального градиента изображения) и плотностью линеаментной сети (пропорциональной локальному градиенту изображения в ортогональном направлении к выделенным штрихам). Эти характеристики также могут быть получены всеми рассматриваемыми ниже методами, но мы не будем на этом останавливаться.
Линеаменты разломов земной коры
Прежде чем мы начнем выделять и анализировать линеаменты (разломы), посмотрим, каким закономерностям они подчиняются. Мы уже знаем о существовании разновременных и разномасштабных планетарных разломов Кто и как поломал Землю, или откуда возникли планетарные горные хребты и разломы, также известных под названием регматической сети. Обратимся за геофизической иллюстрацией механизма их возникновения к работе (Moody, Hill, 1956):

Таким образом, каждое из основных направлений разломов может порождать свою фрактальную структуру согласно иллюстрации выше. Вот иллюстрация ранга и направлений планетарных разломов (регматической сети) (Moody, Hill, 1956):
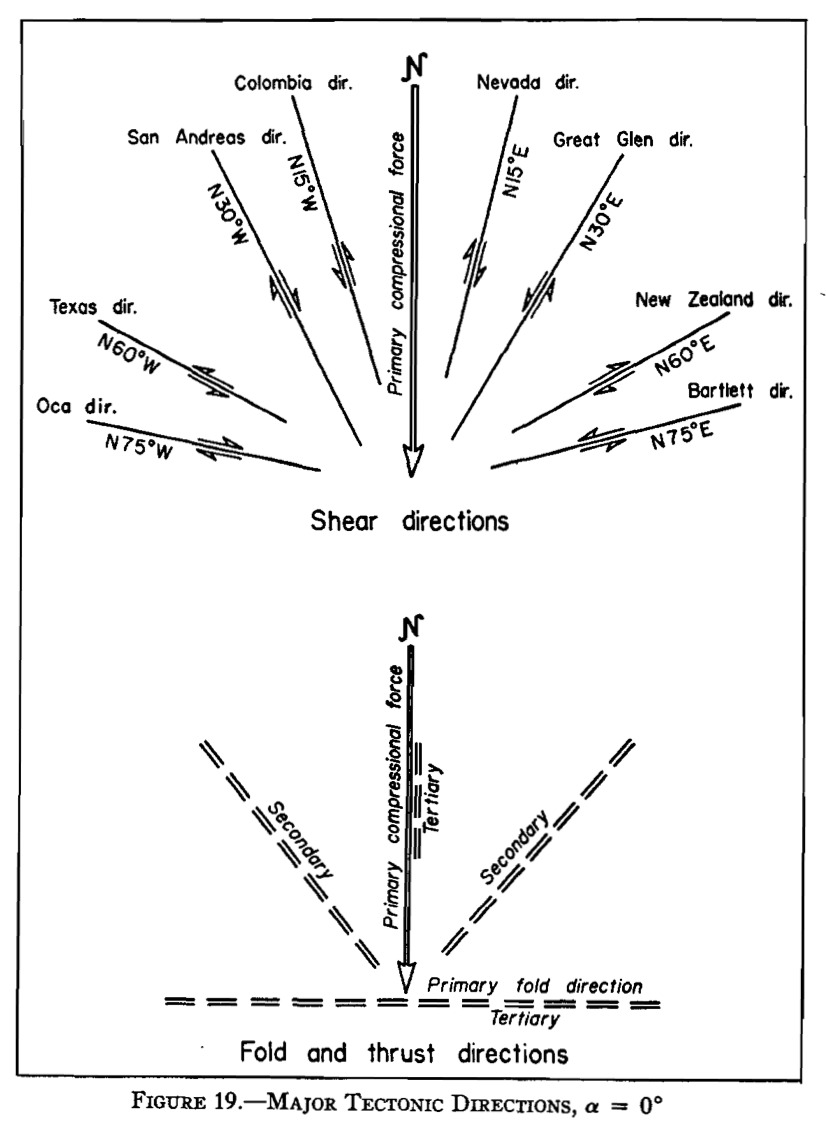
Из этого следует, что вторичные (диагональные) линеаменты моложе линеаментов крестообразного простирания (первичных) и имеют меньший масштаб. Также понятно, что при изменении масштаба анализа мы ожидаем изменения основных направлений линеаментов. Все это мы и будем проверять на дальнейших результатах.
Линеаментный анализ изображений в программе LESSA
Классикой инструментов линеаментного анализа растровых изображений является программа LESSA от Александра Златопольского, демо-версия которой доступна по адресу WinLESSA. Множество публикаций автора программы рассматривают различные практические аспекты и примеры использования линеаментного анализа, смотрите список на сайте программы LESSA и на сайте Институт космических исследований Российской академии наук (ИКИ РАН): Златопольский А.А. Златопольский описал практически найденные закономерности, которым мы можем дать теоретическое описание. Например, реальное (эффективное) разрешение данных оценивается с помощью анализа в LESSA:
Вводится понятие эффективного разрешения. Эффективное разрешение данных характеризует размер самых мелких объектов (деталей), которые присутствуют в этих данных (Златопольский, 2014).
В статье Оцениваем открытые и коммерческие цифровые модели рельефа мы уже рассмотрели, как математически корректно определить реальное разрешение с помощью анализа пространственных спектров данных и планировали в продолжение статьи рассмотреть способ вычислительного увеличения разрешения, используя фрактальность их спектров.
Вот как Златопольский описывает вырожденность высокочастотных спектров исходных данных:
Практически разрешение данных может оказаться меньше заявленного (Е) – т.е. в данных нет самых мелких (по ширине) из возможных объектов. В этом случае можно несколько (в Cd раз) сжать данные без потери информации. Далекая аналогия этой ситуации – теорема Котельникова (если аналоговый сигнал имеет ограниченный по ширине спектр, то он может быть восстановлен однозначно и без потерь по отсчетам, взятым с частотой, строго большей удвоенной верхней частоты) (Златопольский, 2014).
На самом деле, теорема Котельникова здесь полностью применима. Реально существующий рельеф является аналоговым, а его цифровая модель — дискретным. Теорема отсчетов (Котельникова) в пространственной области означает, что на самый мелкий различимый элемент аналогового рельефа должно приходиться не менее 2-х пикселов для возможности восстановления исходного аналогового рельефа без потерь. В случае восстановления с потерями, очевидно, это требование не выполняется. Как показано в статье Оцениваем открытые и коммерческие цифровые модели рельефа, для допустимой ошибки 30 метров реальное разрешение рельефа ALOS World DEM 30m равно 30 м, то есть вдвое выше, чем это возможно для цифровой модели без потерь, а для ошибки 10 см реальное разрешение USGD NED DEM 1m равно 2 м, то есть соответствует теореме. Следовательно, во втором случае можно считать, что цифровой рельеф точно соответствует реально существующему аналоговому при разрешении 2 м и при данном разрешении дальнейшее повышение его вертикальной точности не имеет смысла.
Используя мультимасштабный анализ в LESSA Златопольский предлагает метод вычислительного увеличения разрешения:
Для поиска долин и хребтов в этой работе использована цифровая модель рельефа SRTM с разрешением 0,06511 км/пикс. … Таким образом, благодаря работе с растянутыми данными появилась возможность исследовать тот диапазон масштабов (23 – 65 м/пикс), для которого, как казалось, не было исходных данных (Златопольский, 2014).
Математически это описывается операцией продолжения пространственного спектра в ту область, где он не определен. Как мы показали ранее в Пространственные спектры и фрактальность рельефа, силы тяжести и снимков, спектр мощности рельефа фрактален, то есть линеен в двойных логарифмических координатах, что и позволяет выполнить его расширение в область высоких частот за пределы разрешения цифровой модели.
Также во многих публикациях и на сайте Златопольский разными словами описывает мультимасштабные структуры, хотя при этом не использует термин «фрактал»:
Необходимо учитывать, что, меняя масштаб, мы можем получить не более (или менее) точное описание рисунка, а описание ДРУГИХ рисунков — рисунок структур иных масштабов, которые могут существенно различаться. Очевидно также, что при слишком грубом разрешении можно пропустить базовые структуры, а при слишком высоком разрешении будут выявляться не искомые структуры, а их детали, возможно, с другой ориентацией. LESSA: Методические рекомендации.
Или
Приведены примеры применения этих параметров при мультимасштабном исследовании ориентационных статистических характеристик элементов рельефа. В этом исследовании измеряется и сравнивается среднее направление элементов рельефа разного масштаба (размера). Иногда при небольшом изменении масштаба направление меняется существенно, скачком. Нас, в первую очередь, интересуют «особые масштабы», при переходе к которым направление рельефа изменяется скачком гораздо чаще, чем при переходе к другим масштабам. В работе использованы цифровые модели рельефа Земли (SRTM) и Луны (GLD-100) (Златопольский, 2014).
Здесь следует разделить два эффекта. Первый из них, именно скачкообразное изменение характеристик, связано с использованной методикой анализа. Второе — это сам эффект значительного изменения выделяемых направлений.
Причина первого эффекта заключается в том, что использование для изменения масштаба простой передискретизации искажает пространственные спектры и вызывает вычислительные артефакты вроде нестабильности направлений линеаментов для разных масштабов. При использовании полосовой пространственной фильтрации можно избежать указанных вычислительных артефактов и сосредоточиться на втором, основном, эффекте. Если использовать ту же программу LESSA на изображениях после полосовой гауссовой фильтрации, то неустойчивость решения будет исключена (не будет происходить «смешивание» линеаментов от структур разного пространственного масштаба).
Теперь рассмотрим сам эффект изменения преобладающих направлений, описанный подробно в статьях [Златопольский, 2012, 2013, 2017]. Как мы показали ранее в Оцениваем открытые и коммерческие цифровые модели рельефа, фрактальная размерность сохраняется в очень широком диапазоне масштабов, что означает наличие (фрактальных) объектов на всех масштабов, причем их количество быстро растет при уменьшении масштаба (в силу линейности спектра в двойных логарифмических координатах). Согласно (Moody, Hill, 1956) при изменении масштаба происходит и смена направлений линеаментов. Обратимся к ноутбукам Band-Pass Gaussian Filtering GEBCO 2019 и Band-Pass Gaussian Filtering Sandwell & Smith для контурного мультимасштабного анализа с помощью полосовой пространственной фильтрации глобальных моделей Gebco 2019 Bathymetry и Sandwell & Smith Gravity, как это будет описано далее:

Как видим, изменения направлений линеаментов происходят последовательно при изменении масштаба без резких скачков, связанных с неустойчивостью вычислений. Минимальный масштаб 40 км выбран равным примерно удвоенному разрешению используемых растров. Таким образом, показанная Златопольским проблема успешно решена.
Выбор верного способа изменения масштаба позволяет решить проблему неустойчивости мультимасштабного анализа в LESSA. Поскольку перемасштабирование осуществляется до выполнения самого анализа, это даже не является проблемой LESSA, а просто оказывается вопросом корректной подготовки исходных данных. Замечу, что я сам не использую LESSA, но порой обращаюсь к публикациям Златопольского при интерпретации получаемых результатов.
Розы диаграммы растровых изображений
Начнем мы с самых известных и не обещающих корректность с математической точки зрения алгоритмов, которые в пределе не обеспечивают непрерывное однократное покрытие плоскости, так что устойчивость результатов анализа на разных масштабах не всегда выполняется и необходимо это контролировать.
Нужные нам алгоритмы просты в реализации (даже без использования сторонних библиотек) и, при известном мастерстве их использования, они позволяют получить геологически значимые результаты. Вычислительный алгоритм Хафа, равно как и его вариант Быстрое преобразование Хафа, основан на математическом обратимом Линейном преобразовании Радона и является классикой компьютерного зрения. Соответствующие реализации доступны во множестве Python библиотек, например: scikit-image: Straight line Hough transform и OpenCV: Hough Line Transform. В старых публикациях этот алгоритм обозначался просто как преобразование Хафа (Hough Transform), но после добавления в библиотеки еще и кругового преобразования Хафа первый стали называть линейное преобразование Хафа (Hough Line Transform), а второй — круговое преобразование Хафа (Hough Circle Transform). Последний мы уже рассматривали в статье Методы компьютерного зрения для решения обратной задачи геофизики. Также доступно так называемое вероятностное преобразование Хафа (Probabilistic Hough Line Transform), позволяющее значительно ускорить анализ больших изображений за счет анализа лишь некоторого набора случайно выбранных пикселов (Kiryati et al., 1991). Кроме того, если линейное преобразование находит штрихи, пересекающие все изображение, то вероятностное преобразование позволяет найти и более короткие штрихи.
Практически для вычисления сначала требуется воспользоваться одним из алгоритмов поиска границ (Канни, к примеру) или высокочастотной фильтрацией. Смотрите ноутбук с примером на гитхаб: Straight Line Hough Transform:

Посмотрим теперь примеры практического анализа данных глобальных моделей силы тяжести и рельефа. Если нас интересуют новейшие изменения, следует воспользоваться высокочастотной фильтрацией для выделения нарушений наименьшего масштаба, а для анализа старейших изменений можно использовать низкочастотную фильтрацию для выделения крупных нарушений и один из алгоритмов выделения границ.
Ниже показаны карты высокочастотных компонент силы тяжести и рельефа и выделенные на них штрихи, наложенные на картину тектонических плит, смотрите ноутбуки Gaussian Filtering on Spheroid GEBCO 2019 и Gaussian Filtering on Spheroid Sandwell & Smith:


Здесь мы используем параметры преобразования Хафа по умолчанию. Можно заметить отсутствие вертикальных штрихов, что хорошо видно на розах-диаграммах:

Как видим, эти диаграммы получились вырожденными, поскольку вертикальные и диагональные направления здесь отсутствуют. Поскольку вычисления выполнены на сильно загрубленном растре, необходимо проверить полученные результаты. Для проверки лучше всего выбрать участок в районе экватора, где кривизна поверхности планеты минимальна и видимые длины почти точно соответствуют истинным. Рассмотрим подробнее исходный растр целиком и его увеличенный участок между Южной Америкой и Африкой:

В самом деле, мы видим здесь преобладание субгоризонтальных штрихов, а также присутствуют в заметном количестве диагональные и, единично, вертикальные. Результаты преобразования Хафа зависят как от масштаба, так и от параметров преобразования, и зачастую удобнее варьировать именно масштаб. Рассмотрим линеаменты указанной части изображения в ноутбуках Gaussian Filtering on Spheroid GEBCO 2019 и Gaussian Filtering on Spheroid Sandwell & Smith:


Полученные картинки выглядят очень похоже на аналогичные для всей поверхности планеты. Обратимся к розам диаграммам выбранного участка:
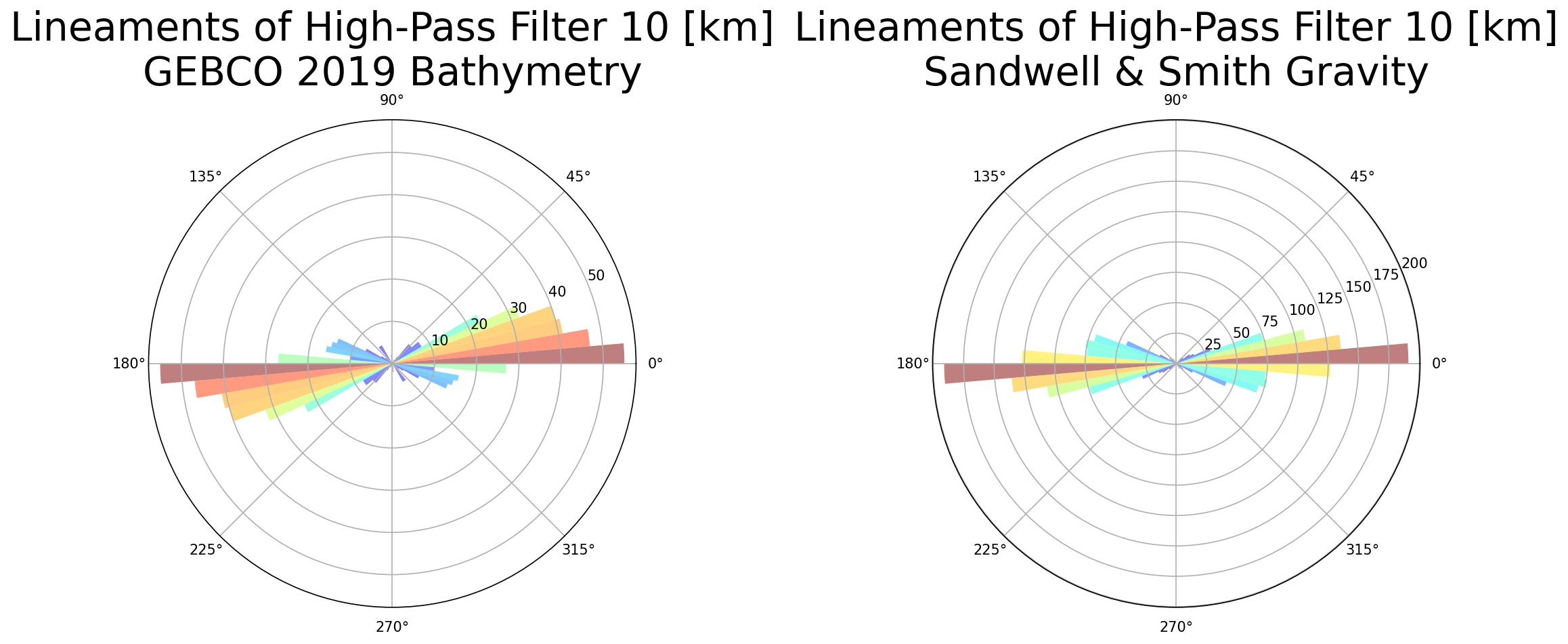
Как видим, результаты почти совпадают с полученными выше для всей планеты. Следовательно, проводимый анализ вычислительно устойчив и эти результаты пригодны для геологического анализа.
Анализ растров с помощью алгоритмов Хафа чувствителен к масштабу и заданным параметрам и находит лишь некоторое количество штрихов, не обеспечивая никаких гарантий, что именно найденные являются наиболее значимыми. Поскольку требуемые параметры (длина выделяемых штрихов и прочие) определяются выбранным масштабом, во многих случаях возможно использование параметров по умолчанию и изменение только масштаба. Необходимы сравнение и экспертная оценка получаемых результатов, непосредственное их использование для дальнейшей обработки недопустимо. Несомненными плюсами являются простота использования метода и его визуальная наглядность.
Розы диаграммы векторных данных
С помощью векторизации объектов на растровом изображении можно построить векторные карты. Существуют разнообразные методы векторизации, например, путем трассирования штрихов с помощью преобразования Хафа, рассмотренного выше, и других алгоритмов, а также вручную. Очевидно, качество полученных векторных данных варьируется в очень широких пределах, так что требуется тщательная оценка и проверка самих данных и получаемых результатов.
Для примера рассмотрим открытые мультимасштабные карты береговой линии и центральных линий рек от Natural Earth. Посчитаем направления и количество сегментов, как показано в ноутбуках Natural Earth Coastline и Natural Earth Rivers. Обратите внимание на подготовку исходных данных — необходимо исключить азимуты, в точности равные 0° и 180°, поскольку они явно оказываются артефактами векторизации, как это показано для угловых распределений длин сегментов. Сначала посмотрим данные масштаба 1:10 миллионам и, соответственно, наибольшей детализации в ноутбуках Natural Earth Coastline и Natural Earth Rivers:

Судя по всему, мы здесь видим направления для несколько масштабов разом. Вероятно, данная векторная карта собрана из частей разной детальности с последующей совместной их генерализацией.
Аналогом низкочастотной фильтрации растровых данных является использование векторных данных большего масштаба 1:50 миллионам и меньшей детализации в ноутбуках Natural Earth Coastline и Natural Earth Rivers:

На этих диаграммах сложно выделить какие-либо преобладающие направления, поскольку отсутствует значительная разница между всеми направлениями, что обусловлено генерализацией данных Natural Earth для уменьшения размера данных (количества сегментов векторов).
В качестве источника различных векторных данных можно использовать OpenStreetMap (OSM) в виде регулярных дампов в различных форматах на странице проекта GEOFABRIK. Для разработчиков может пригодиться мой проект bigquery-openstreetmap, где для всех слоев данных GEOFABRIK доступны SQL скрипты их извлечения из полного дампа OSM на платформе Google BigQuery. Замечу, что путем легкой модификации эти же скрипты могут быть использованы с любой другой базой данных или непосредственно для извлечения данных из бинарного дампа OSM. Конечно, эти данные требуют предварительной проверки, так как данные OSM имеют совершенно разное качество для разных территорий.
Как показано выше, результат анализа векторных данных, очевидно, определяется качеством исходных данных. Анализ возможен лишь для тех масштабов, для которых предоставлены исходные данные, причем результат анализа может относиться к другому или другим масштабам, отличным от заявленного для используемых данных. В отличие от вышеописанных методов, плюсом является отсутствие каких-либо параметров. При этом, необходимо производить предварительную оценку и очистку исходных данных.
Розы диаграммы контурных карт
Контурные карты обладают двумя важнейшими для нас свойствами: они обеспечивают непрерывное покрытие плоскости (в пределе при уменьшении шага изолиний) и их можно построить полностью автоматическими методами. Очевидно, что сегменты, из которых состоят выделенные изоконтуры, и являются штрихами в терминах линеаментного анализа, остается лишь найти среди них преобладающие направления. Для таких данных возможен корректный мультимасштабный анализ.
В качестве примера обратимся к растрам глобальных моделей гравитационного поля и рельефа из предыдущей части статьи и выполним автоматическое их оконтуривание с последующим анализом направлений сегментов контуров. Начнем с анализа исходных растров в ноутбуках GEBCO 2019 и Sandwell & Smith:

На полученных диаграммах мы наблюдаем диагональные и горизонтальное направления простирания линеаментов. Далее построим аналогичные розы-диаграммы с теми же параметрами высокочастотной фильтрации, как и выше (для ускорения обработки фильтров большего радиуса воспользуемся фильтрацией на плоском растре вместо фильтрации на эллипсоиде) в ноутбуках High-Pass Gaussian Filtering GEBCO 2019 и High-Pass Gaussian Filtering Sandwell & Smith:

Здесь присутствуют все направления и явно выражены диагональные пики, что соответствует новейшей диагональной системе линеаментов и согласуется с Кто и как поломал Землю, или откуда возникли планетарные горные хребты и разломы Для двух вариантов низкочастотной фильтрации модели гравитационного поля получаем следующие результаты в ноутбуке Low-Pass Gaussian Filtering Sandwell & Smith:

Как и ожидается, при увеличении масштаба выделяются субвертикальные и субгоризонтальные линеаменты, причем первые здесь выражены сильнее. Следует обратить внимание, что на исходных растрах вертикальное простирание вовсе не выделялось. Полученные результаты согласуются с ожидаемыми и, притом, вычислены полностью автоматически. Таким образом, наиболее важные результаты можно получить только при мультимасштабном анализе, выделяя диапазоны масштабов с помощью полосовой фильтрации, при этом основные направления определены в работе (Moody, Hill, 1956).
Итак, автоматическое оконтуривание растровых данных обеспечивает прекрасные результаты. При дальнейшем использовании недетерминированных алгоритмов, например, методов машинного обучения, использование проверенных векторных данных или фильтрация растровых данных и дальнейшее их оконтуривание и последующий анализ направлений позволяют построить автоматизированный процесс обработки (pipeline). А для решения семантических задач, связанных с выделением и раздельным анализом объектов разных классов, необходимы иные методы.
Розы диаграммы геометрических графов
Для получения графового представления растровых данных мы можем воспользоваться методами триангуляции поверхности. Так нам становятся доступны множество методов анализа, включая выделение линеаментов с помощью построения центральной линии, каркаса графа (остовного дерева) и так далее. Поскольку триангуляция гарантирует непрерывное покрытие поверхности (в пределе при уменьшении размера ячейки), корректный анализ возможен для всех масштабов. Графовое представление позволяет выполнять семантическую сегментацию и анализ, в том числе, выделение и ранжирование гидросети как линий потока и решение других намного более сложных задач, нежели предыдущими методами. Кроме того, возможно использование методов машинного обучения непосредственно на графах на любом этапе анализа.
Для анализа воспользуемся соответствующим разделом математики — геометрической теорией графов. Эта теория рассматривает вложения графов в пространства, при которых рёбра представляются отрезками, что применимо и к сетчатым поверхностям. Как раз сетчатые поверхности мы используем чаще всего для представления растров, смотрите статью Как визуализировать и анимировать (геофизические) модели. Воксельные модели и сетчатые поверхности, и для моделирования, как показано в Гидродинамическое моделирование (CFD) на рельефе с помощью MantaFlow и визуализация результатов в ParaView. Таким образом, нас интересуют свойства геометрических графов при изменении масштаба и выделение на них особых направлений или асимметрий.
Если обратиться к литературе по применению теории графов в геодезии и картографии, мы найдем математическое описание упрощения топологии графов, то есть изменения их детализации (масштаба) (Самсонов et al., 2014):
Алгоритм упрощает линии путем стягивания ребер графа с сохранением глобальной топологии, т.е. с сохранением относительного взаимного расположения объектов относительно друг друга, что позволяет одновременно обрабатывать несколько слоев. Произведена количественная оценка результатов. Методика может использоваться в различных задачах, связанных с упрощением и сжатием данных, в том числе при мультимасштабном картографировании (Самсонов et al., 2014).
Теория графов также рассматривает меру фрактальности, хотя используются иные обозначения. В той же статье мы и найдем описание фрактальности (Самсонов et al., 2014):
А. М. Берлянт, О. Р. Мусин и Т. В. Собчук [1] исследовали поведение таких величин, как извилистость, удельная кривизна и длина линии при уменьшении масштаба на примере генерализации. В качестве меры извилистости они использовали простой коэффициент, выражающий число изгибов на единицу длины линии. Анализ карт различных масштабов привел их к выводу о том, что кривизна линий уменьшается при переходе к более мелкому масштабу, в то время как длина и извилистость не имеют масштабной зависимости (Самсонов et al., 2014).
Как мы и следовало ожидать (Самсонов et al., 2014):
Теория графов показала себя эффективной при генерализации картографических данных [11] (Самсонов et al., 2014).
Учитывая, что фрактальная размерность (фрактальность) является морфологическим параметром, а пространственная фильтрация объединяет (коллапсирует) детали мелкого масштаба, выводы в обсуждаемой статье становятся понятны (Самсонов et al., 2014):
В качестве перспектив дальнейших исследований следует назвать внедрение морфологического анализа линий, а также разработку подхода, осуществляющего коллапс циклов (разветвлений) в осевые линии (Самсонов et al., 2014).
При этом, как мы уже показали в Пространственные спектры и фрактальность рельефа, силы тяжести и снимков, при гауссовой пространственной фильтрации значение фрактальности сохраняется с высокой точностью в широком диапазоне масштабов, значительно превосходя результаты, полученные (Самсонов et al., 2014). Следовательно, пространственная гауссова фильтрация растра и построение для него сетчатой поверхности равнозначно топографическому упрощению (генерализации) соответствующего геометрического графа исходного растра. При этом, очевидно, полученный граф не является оптимальной генерализацией ни по количеству узлов, ни по суммарной длине ребер. Топографическое упрощение сетчатой поверхности позволяет получить направления асимметрии и сохранить значение фрактальной размерности.
Графовые методы анализа имеют значительные преимущества, поскольку для них не требуются априори заданные параметры, они анализируют все ребра графа, а также обрабатывают информацию о высоте, но вычислительно такой подход более сложен. При использовании корректно подготовленных исходных данных получаемые результаты достоверны и не требуют их экспертной оценки. При дальнейшем использовании недетерминированных алгоритмов, например, методов машинного обучения, именно графовые методы позволяют построить автоматизированный процесс обработки (pipeline).
Заключение
В статье мы рассмотрели линеаментный анализ, начиная от самого предмета изучения и базовых растровых алгоритмов анализа и до современных векторных и графовых методов. Если первые из них вообще не претендуют на корректность и лишь на некоторых отдельных масштабах позволяют получить определенные результаты, то последующие являются математически корректными и обеспечивают возможности мультимасштабного анализа. Представленные Python ноутбуки помогут ознакомиться с различными методами и использовать их для решения практических задач, а для помощи в геологической интерпретации результатов приведены ссылки на соответствующую литературу.
Хотя я и собирался проиллюстрировать все разделы статьи соответствующими примерами геологических исследований, объем статьи уже превысил мои ожидания, так что отложим это до следующих публикаций.
Ссылки
Kiryati, N., Eldar, Y., & Bruckstein, A. M. (1991). A probabilistic Hough transform. Pattern Recognition, 24(4), 303–316.doi:10.1016/0031-3203(91)90073-e
Moody, J.D., and Hill, M.J., 1956, Wrench-fault tectonics: Geological. https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.1005.7003&rep=rep1&type=pdf
Методика изучения и анализа трещиноватости. Часть 2. Графические методы изображения замеров ориентировки трещин и анализ трещиноватости. Пустовит О.Е., Попов Ю.В. Учебно-методическое пособие для бакалавров и магистров по направлению «Геология». — Ростов-на-Дону: ЮФУ. 2009. 34 с., 11 рис., 2 табл. https://www.geokniga.org/bookfiles/geokniga-metodika-izucheniya-i-analiza-treshchinovatosti.pdf
Самсонов Т. Е, Якимова О. П., Алексеев В. В., Богаевская В. Г., Горохов А. А., Князев В. Н., Преображенская М. М., Ухалов А. Ю., Эдельсбруннер Х. Алгоритм геометрического упрощения множества линий путем стягивания ребер графа с сохранением топологии. // Геодезия и картография. 2014. № 3. С. 29-36. https://istina.msu.ru/download/6113601/1fmJUX:pmkx2-s340UeBNIc6oLDZ-jiu5E/
Златопольский А.А. Новые возможности технологии LESSA и анализ цифровой модели рельефа. Методический аспект // Современные проблемы дистанционного зондирования Земли из космоса. 2011. Т.8. № 3. С. 38-46. http://d33.infospace.ru/d33_conf/2011v8n3/38-46.pdf
Златопольский А.А. Эффективное пространственное разрешение данных и инструмента. На примере мультимасштабного анализа ЦМР. // Современные проблемы дистанционного зондирования Земли из космоса. 2014. Т.11 № 2. С. 18-25. http://d33.infospace.ru/d33_conf/sb2014t2/18-25.pdf
Златопольский А.А. Мультимасштабный анализ ориентации текстуры поверхности Земли. Особые масштабы // Современные проблемы дистанционного зондирования Земли из космоса. 2012. Т. 9. № 3. С. 26-37. http://d33.infospace.ru/d33_conf/sb2012t3/26-37.pdf
Златопольский А.А. Мультимасштабный анализ ориентации текстуры поверхности Земли. Особые масштабы. Вторая часть // Современные проблемы дистанционного зондирования Земли из космоса. 2013. Т.10. № 2. С. 295-306. http://d33.infospace.ru/d33_conf/sb2013t2/295-304.pdf
Златопольский А.А. Мультимасштабный анализ ориентации текстуры поверхности Земли. Особые масштабы. Третья часть. Иерархия долин // Современные проблемы дистанционного зондирования Земли из космоса. 2017. Т. 14. № 5. С. 37-46. DOI: 10.21046/2070-7401-2017-14-5-37-46. http://d33.infospace.ru/d33_conf/sb2017t5/37-46.pdf

