
Ранее я уже писал про приложения теории графов: тут и тут.
В этой статье хочу помочь коллеге в теории графов – он пожаловался в комментарии к своей статье, что:
Здесь я попытался в максимально доступной форме объяснить, как же это делать. И в первую очередь я делаю это для студентов, которые изучают данную тему и могут не понимать, зачем вообще графы нужны. Учась, я лично убедился, что для многих эта тема была «проходной» и они не извлекли из нее никакой ценной информации, а также так и не поняли, как работать с матрицами.
На это я ответил:
ИМХО для IT-студентов нужно сразу сказать, что списки (стеки, очереди) и бинарные деревья это графы. И всякие схемы, типа схемы метро, автодорог, принципиальные в электронике можно рассматривать как графы. Приложения теории графов — это фундаментальные свойства всяких подобных схем.
Для студентов историков м.б. будет полезно узнать, что фамильные деревья — это графы. И проч. др. специальности. Где только нет графов, пусть на уровне тривиального списка. Возвращаясь к IT: строка символов — граф, и число — последовательность байт — граф, и файл — граф, не говоря о БД.
Дисклеймер. Далее хочу высказать свое сугубо личное мнение, никого ни в чем, не пытаясь убедить или переубедить. Исключительно в порядке обсуждения. Т.о. я адресуюсь к читателям, уже знакомым с теорией графов. Нижеследующее — всего лишь мои предположения. Иногда я опираюсь на факты и на авторитеты (Харари, Зыков, Вирт, Адельсон –Вельский и, как ни странно, А. Дюма), но это не повод тотально засадить всех студентов за зубрежку теории графов в полном объеме.
Вернемся к историкам. Предположим, что ими собрано достаточно документов о том, что у Хуана и Хуаниты, после того, как они сочетались законным браком, было пять детей. Но Хуанита изменяла Хуану и двоих родила внебрачно. А Хуан не остался в долгу и трижды изменил Хуаните – еще двое детей. Однако вопрос: от кого из любовников родила Хуанита?: От Филиппа или от кардинала Ришелье? А может от кого-то из четырех мушкетеров – он была общительной женщиной. Такой вопрос и про Хуана: он был знаком и пользовался расположением королевы Франции, но уделял внимание и ее дамам. (А. Дюма на многих сотнях страниц описывает подобные истории).
Как видим из этого модельного примера — граф (фамильное дерево) можно описать на естественном языке. Но для наглядности его лучше нарисовать, а как будет лучше?
Можно так:

Где черные ребра – документально подтвержденные факты, а красные – предположения.
А можно так:
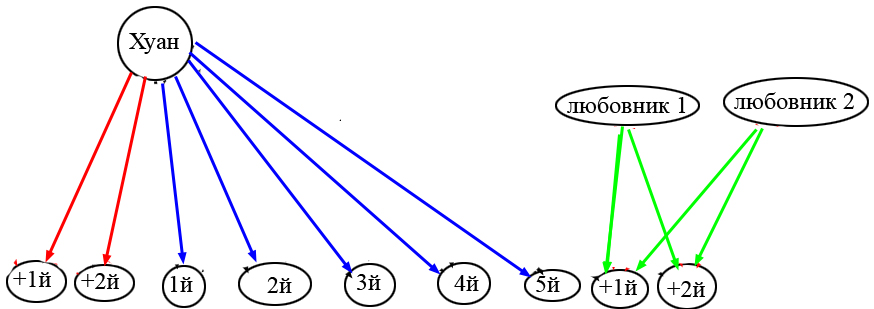
Где красные ребра имеют надпись: "+любовница 1 или + любовница 2 или + любовница 3", т.е. предположения.
Синие и зеленые ребра имеют надпись: "+Хуанита", но синие — документально подтвержденные факты, а зеленые – предположения.
Сделаем определения:
Путь — это результат обхода некоторых вершин графа по правилу: переходить можно только на вершну инцидентную (т.е. связанную ребром) текущей вершине. При этом нельзя возвращаться по уже пройденному ребру.
Цикл – это путь начало, которого и конец, которого в одной и той же вершине.
Пример:
Это цикл:
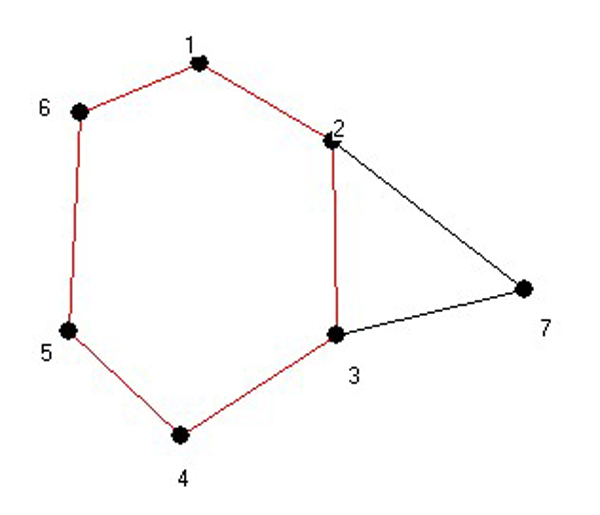
И это цикл:

Еще определения:
Дерево – это граф без циклов.
Пример:

Линейный список – дерево без ветвей. Т.е. только предыдущий элемент списка всегда инцидентен следующему и никакой другой.
Пример:
т-о-л-ь-к-о- -п-р-е-д-ы-д-у-щ-и-й- -э-л-е-м-е-н-т- -с-п-и-с-к-а- -в-с-е-г-д-а- -и-н-ц-и-д-е-н-т-е-н- -с-л-е-д-у-ю-щ-е-м-у
Здесь буквы и пробел – вершины графа, а дефис “-” обозначает ребро.
Г.М. Адельсон-Вельский доказал, что время поиска по дереву зависит от высоты этого дерева. (Н.Вирт в своей знаменитой книге “Алгоритмы + структуры данных = программы” ссылается на эту работу.) Из доказательства Адельсона-Вельского следует, что наихудший случай для дерева – вырождение в линейный список, и, следовательно, превращение списка в достаточно развесистое дерево ускорит поиск.
Для иллюстрации возьмем рекурсивное определение Вирта бинарного дерева.
Type
link = ^node;
node = record
left, right : link; // левое и правое поддеревья
dat : // любой тип, допускающий сравнение: integer, string, real
// и т.д.
end; // record nodeРекурсивная процедура сортировки будет такая:
procedure add (var currNode : link; aDat :// любой тип, допускающий
// сравнение
);
begin
if currNode = nil then
begin
new ( currNode); // создать новое поддерево
currNode^.left := nil; // без ветвей
currNode^.right := nil;
currNode^.dat := aDat
end
else
if currNode^.dat> aDat then
add (currNode^. right, aDat) // добавить к правой ветви
else
if currNode^.dat< aDat then // if №2
add (currNode^. left, aDat) // добавить к левой ветви
else // currNode^.dat = aDat, здесь нужно доп.решение,
// но для простоты считаем, что все aDat уникальные, т.е. if №2 не нужно
end;// procedure add Функция поиска в дереве:
function find (currNode : link; aDat ://любой тип, допускающий сравнение
) : link;
begin
if currNode= nil then
find := nil // вернуть: ничего не найдено
else
if currNode^.dat> aDat then
find := find (currNode^. right, aDat)
else
if currNode^.dat< aDat then
find := find (currNode^. left, aDat)
else
if currNode^.dat = aDat then
find := currNode //вернуть результат
end;// function findКак сделать развесистое дерево из отсортированного списка – отдельная проблема. Может добавлять в дерево случайным образом, а может использовать алгоритмы балансировки деревьев.
Для гуманитариев может и не нужно вникать в приведенный код. Им важно понять, что список:
Аня
Ваня
Иван Васильевич
и т.д.
не всегда оптимальное решение. Не смогут сами — попросят помочь.
Я (с коллегами) продемонстрировал быстрый поиск при размерности ок.100 лимонов химических соединений (не все реально полученные – некоторые гипотетические). Тут мы встречаемся с важной задачей теории графов – задачей установления изоморфизма двух графов.
Классическая теория графов смотрит только на топологию: какая вершина с какой связаны ребром, а геометрию рисунка не учитывает. Такой подход оказался продуктивным для обобщений и теорем. Но проблема в том, что на листе бумаги мы можем произвольно отметить n точек или кружочков по числу вершин графа, произвольно пронумеровать эти вершины и соединить их линиями, обозначающими ребра. Рисунки одного и того же графа не обязательно совпадут в своей геометрии.
Пример не похожих рисунков:
Кубан – кунеан. Это химическая реакция перехода химического вещества кубан в вещество кунеан. Можно видеть, что структурные формулы органической химии не отличаются от графов.
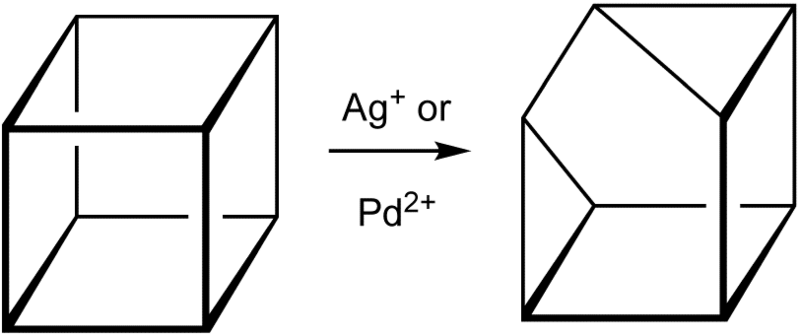
И этот кунеан на другом рисунке:

Математически в общем случае задача изоморфизма сводится к поиску матрицы перестановки такой, чтобы
A1= TA2P,
где A1 – матрица смежности первого графа;
A2 – матрица смежности второго графа;
P — матрица перестановки;
T – обратная ( = транспонированная, для данного случая) матрица перестановки.
На словах понятно, что если удается найти для второго графа такую нумерацию, что смежность вершин совпадает с первым (говорят “найти биекцию” — см. Википедию)
к примеру, если в одном графе есть ребро между первой и второй вершинами и в другом графе такое ребро, и так для всех ребер, то графы изоморфны – фактически это один и тот же граф.
Нужно отметить, что для некоторых типов графов задача изоморфизма решается тривиально, для других легко, но для многих требует перебора со сложностью в экспоненту. Тривиально для полных графов – это графы, у которых каждая вершина связана со всеми остальными (инцидентна всем остальным). Понятно, что для любых n вершин существует только один полный граф. Поэтому проверка на изоморфизм сводится к проверке равенства числа вершин первого графа = числу вершин второго. Аналогично для безреберного графа (где только вершины).
Легко задача изоморфизма решается для случая, когда у всех вершин разные степени. Т.к. степени уникальны, то вычисление матрицы перестановки не требуется – простая перенумерация. Каждому номеру вершины второго графа присваиваете номер вершины первого той же степени и проверяете совпадение ребер.
Но не у всех графов степени вершин уникальны. Тут появляются идеи канонической нумерации, т.е. нумерации вершин по жестким однозначным правилам, и полного инварианта графа. Инвариант это обычно (но не обязательно) число, которое не меняется от перенумерации вершин графа. Примером инварианта может служить сумма степеней вершин.
Очевидно, что у двух неизоморфных графов эти инварианты могут совпадать. (Если инварианты не совпадают, то графы точно не изоморфны).
Полные инварианты это, которые, если равны, то графы изоморфны, а если не равны, то не изоморфны. Один из полных инвариантов описан у Зыкова. Матрицу смежности можно развернуть в вектор – нужно просто добавлять в вектор строку за строкой из матрицы. Этот вектор можно рассмотреть, как двоичное число. Можно перебрав все матрицы найти минимальное и максимальное числа. Далее если такие минимальные (или максимальные) числа для двух графов совпадают, то, очевидно, что их матрицы смежности после перестановки будут равны и графы будут изоморфны. К настоящему времени не известен ни один полный инвариант, который можно вычислить без перебора.
Отметим, что изоморфизм деревьев определяется (без полного перебора) с полиномиальной сложностью. А проблема изоморфизма графов остается по-прежнему открытой.
Выше мы затронули проблему отрисовки графов или, как говорят, визуализации. Было предложено много способов (я может, раскачаюсь написать про наиболее полезные), но ни один из них не универсальный. И поэтому графы все рисуют по разному и люди и компьютеры. Я рисую на сделанном мной инструменте.
Возвращаясь к студентам, с которых начал. Думаю, что каждый понимает, что в избранной им области есть структуры. Иногда очень сложные, иногда не очень. Надеюсь мне удалось показать, что теория графов – это теория структур, и учит общим методам обращения со структурами. Может не всем студентам нужно углубляться в эти методы, но понимание общих принципов полезно всем. При этом я не призываю грузить студентов-философов матричной алгеброй – им и так хватает, им положено Платона с Аристотелем читать. Но обзорные лекции будет полезно прослушать со сдачей не сложного зачета, чтобы не прогуливали.
В начале я сказал, что хочу высказать свое сугубо личное мнение, никого не в чем не пытаясь убедить или переубедить. Исключительно в порядке обсуждения. Надеюсь на интересное обсуждение, которое обещает мне много новых знаний о преподавании теории графов для различных специальностей, и о пользе этой теории для этих специальностей.
Использованная литература:
- А.Дюма, Три мушкетера
- Ф.Харари, Теория графов, М.: УРСС, 2003.
- А.А.Зыков, Основы теории графов, М.: Вузовская книга, 2004.
- Н.Вирт, Алгоритмы+структуры данных=программы, М.: Мир,1985.
- П.Грогоно, Программирование на языке Паскаль, М.: Мир,1982
Алгоритмы теории графов:
- Кристофидес, Теория графов. Алгоритмический подход, М.: Мир, 1978 (м.б. есть болеее новые переиздания).
- В.Липский, Комбинаторика для программистов, М.: Мир, 1988.
- В.Н.Касьянов, В.А.Евстигнеев, Графы в программтровании: обработка, визуализация и применение, Спб: БХВ-Петербург, 2003.
Про достижения в решении проблемы изоморфизма графов можно посмотреть:
- Л.И.Малинин, Н.Л.Малинина, Изоморфизм графов в теоремах и алгоритмах, М.: URSS, 2009.
- McKay, Brendan D. (1981), "Practical graph isomorphism", 10th. Manitoba Conference on Numerical Mathematics and Computing (Winnipeg, 1980), Congressus Numerantium, 30, pp. 45–87, MR 0635936.
- Пономаренко И. Н. Проблема изоморфизма графов: Алгоритмические аспекты
Комментарии (15)

OBIEESupport
03.08.2021 15:57Добрый день, автор!
Я минусую за это : "Дисклеймер. Далее хочу высказать свое сугубо личное мнение, никого ни в чем, не пытаясь убедить или переубедить. Исключительно в порядке обсуждения. Т.о. я адресуюсь к читателям, уже знакомым с торией графов. "
Да, я бывший преподаватель университета. Да, графы я преподавал. Да, в моей первой статье на Хабре написано, где проходит граница современных исследований. Пожалуйста, не показывайте читателям вашей полной некомпетентности в теории графов - не поймут. Даже отечественные авторы ушли уже далеко вперед от тех "теоретических" предположений, которые вы имели бесчестье тут написать.

third112 Автор
03.08.2021 16:35Добрый день, читатель!
Да, в моей первой статье на Хабре написано, где проходит граница современных исследований
Не нашел у Вас статьи про графы. Пожалуйста, укажите конкретно.
Даже отечественные авторы ушли уже далеко вперед от тех "теоретических" предположений, которые вы имели бесчестье тут написать.
А можно конкретнее? В чем я не прав?

third112 Автор
03.08.2021 17:16Даже отечественные авторы ушли уже далеко вперед
Почему "Даже"? Считаете, что все отечественные авторы плохие спецы в теории графов? Я упомянул несколько всемирно известных имен: Адельсон-Вельский, Зыков, Малинины (отец и дочь), Пономаренко, Касьянов и Евстигнеев. Могу еще назвать, но думаю, что упомянутых достаточно. Себя называть не буду, хотя печатаюсь в J of Math Chem, и из J of Graph Theory мне рукописи на рецензию присылают ;) Кое-что написал в ru и en Википедии.
Если отечественные авторы плохие спецы, то как обяснить, что крупные издательства, нпр., Springer издают наши переводные научные журналы и деньги за статьи нашим авторам платят?

OBIEESupport
03.08.2021 20:00Дерево – это граф без циклов. ---- формально, надо вводить ориентацию, чтобы соответствовало рисунку.
Г.М. Адельсон-Вельский доказал, что время поиска по дереву зависит от высоты этого дерева. ---- пожалуйста, дайте определение AVL деревьев, если можно, то и с формулируйте основную теорему поиска. "достаточно развесистое дерево" ускорит поиск. --- в книге Г.М. Адельсон-Вельского есть понятное и простое определение этого факта (да, то самое, на котором я люблю студентов заваливать, там логарифм и округление вверх стоит).
Я (с коллегами) продемонстрировал быстрый поиск при размерности ок.100 лимонов химических... --- может быть, миллионов? Если да, то вам должна быть известны не только правила русского языка, но и теорема об изоморфизме деревьев. Да вот незадача-то, большинство химических соединений имеют не только "древовидное", но и "циклическое" строение. То есть классическая теорема об изоморфизме деревьев не работает. Книга Малининых вряд ли про химию.)
Начало атаки на проблему изоморфизма было сделано тут: Изоморфизм графов с ограниченным параметром /В. Н. Земляченко, Н. М. Корнеенко, Р. И. Тышкевич. - Минск : Институт математики, 1982. - 51 с.-(Препринт ; № 5 (130)), а потом народ как прорвало. Я замечу, что никто сначала не делил проблему изоморфизма между классами графов.
Однако дальше вы пишите: "А проблема изоморфизма графов остается по-прежнему открытой". -- нет, ряд работ наших российских ученых и несколько работ зарубежных ученых опровергают ваши слова.
"Я рисую на сделанном мной инструменте." -- согласен, есть есть сложность в визуализации, если бы вы даже намекнули, что уже составили отрисовки всех органических соединений из справочника Бельштейна, это уже было бы шагом вперед, но есть и более полные справочники. И по реакциям тоже. Например, справочник соединений Американского химического общества.
Далее, если вы считаете, что https://youtu.be/zvXeuxUA98Q нормальное изложение проблемы, то не стоит этим пугать студентов, это же не обзор, а выступление на заданную тему.(
Лучше тогда https://www.ozon.ru/product/grafy-berzha-izomorfizm-dekompozitsiya-raskraski-30041461/ , где точно есть теорема про изоморфизм произвольных графов, и решение задачи 4 красок.
Есть еще множество работ, которые могли бы найти отражение в вашей статье, но не нашли.
Из моей статьи привожу задачу, которая встретилась в собеседованиях.
Задача. За окном стоит береза. На ней, как подсчитали ваши коллеги, 100 000 листьев, диаметр ствола у корня — 60 сантиметров. Запишите указанные параметры в любой математической нотации. И докажите ее пригодность: для переписки с коллегой, так как дерево хотят спилить. Или для компьютерной обработки ее изображения.
Ближе к тематике сайта статья "СТРАТЕГИИ ПРОВЕРКИ КОРРЕКТНОСТИ МЕТОДА ВЫЯСНЕНИЯ ИЗОМОРФИЗМА ГРАФОВ С ИСПОЛЬЗОВАНИЕМ ГРИД-СИСТЕМ НА ДОБРОВОЛЬНОЙ ОСНОВЕ" Э.И. Ватутин, В.С. Титов, где авторы не размахивают руками, а численно проверяют инварианты изморфизмов графов, найденные ими в их более ранних работах.

third112 Автор
03.08.2021 22:35+1Спасибо за ответ.
Дерево – это граф без циклов. — формально, надо вводить ориентацию, чтобы соответствовало рисунку.
Формально, не очень удачный рисунок из вики. А где ошибка? Если стрелочки просто линиями заменить, то это дерево останется деревом.
дайте определение AVL деревьев
Надейюсь, из Вики устроит:
АВЛ-дерево — сбалансированное по высоте двоичное дерево поиска: для каждой его вершины высота её двух поддеревьев различается не более чем на 1.
И что неверного в моей фразе про высоту? Алгоритмы балансировки дерева в обзорной статье, как моя, считаю излишними. Иначе студент не увидит леса из-за сбалансированных деревьев ;)
может быть, миллионов?
Верно. Я использовал вольности языка, принятые на Хабре. А Вы поняли, но придрались.
Да вот незадача-то, большинство химических соединений имеют не только "древовидное", но и "циклическое" строение.
И где я утверждаю обратное? Где сказал, что в органике нет циклов?
Книга Малининых вряд ли про химию.
Да эта книга не про химию. И что из этого следует?
Я замечу, что никто сначала не делил проблему изоморфизма между классами графов.
Я писал не про историю вопроса: что сначала, что потом. Зачем? Может с начала времен начать? Написать, что когда наши предки — пещерные люди выходили на охоту с "кирпичом" на мамонта, они не знали про графы, м.б. только догадывались. Это важно добавить в статью? Те люди хорошо ориентировались на местности — жизнь заставляла, они всегда знали куда бежать, когда на мамонта, а когда от мамонта. Кто не знал — тот не выжил. Но я не об этом пишу. Многие преподы, желая понравиться студентам, начинают с мамонтов и переходят на работы, которые сейчас имеют исторический интерес.
"А проблема изоморфизма графов остается по-прежнему открытой". — нет, ряд работ наших российских ученых и несколько работ зарубежных ученых опровергают ваши слова.
Кто доказал, что изоморфизм 2 графов можно/нельзя найти за полиномиальное время?
Не только я не знаю, но и Вики ;) Читаем:Хотя задача распознавания изоморфизма графов принадлежит классу NP, неизвестно, является ли она NP-полной или принадлежит классу P (при условии, что P ≠ NP).
Про отдельные классы графов много интересных работ. Нпр., про сильно регулярные графы.
вы даже намекнули, что уже составили отрисовки всех органических соединений из справочника Бельштейна,
В Бельштейне достаточно структурных формул. Зачем там еще что рисовать? Другое дело, что поиск там непростой — студентов специально учат.
Лучше тогда https://www.ozon.ru/product/grafy-berzha-izomorfizm-dekompozitsiya-raskraski-30041461/, где точно есть теорема про изоморфизм произвольных графов, и решение задачи 4 красок.
Про 4 краски не сказал ни слова. Это отдельная тема, про которую еще не так давно спорили — сейчас немного утихли И, да, есть много теорем. Но основной вопрос про изоморфизм остается открытым.
Есть еще множество работ, которые могли бы найти отражение в вашей статье, но не нашли.
Да! Есть! Тогда бы моя статья превысила все мыслимые пределы.
Задача. За окном стоит береза
Не вижу смысла этой задачи. Прошу Вас растолкуйте.
Можно написать: береза: (листьев:100 000; диаметр ствола: 60). И что?Ближе к тематике сайта статья "СТРАТЕГИИ ПРОВЕРКИ КОРРЕКТНОСТИ МЕТОДА ВЫЯСНЕНИЯ ИЗОМОРФИЗМА ГРАФОВ С ИСПОЛЬЗОВАНИЕМ ГРИД-СИСТЕМ НА ДОБРОВОЛЬНОЙ ОСНОВЕ" Э.И. Ватутин, В.С. Титов
Помню Ватутина по Вики, писали с ним про графы. Оставил отличные впечатления, как спец и как человек. В статье читаем:
Приведено описание стратегий проверки методов выявления изоморфизма графов путем организации попарного сравнения матриц смежности графов выбранной размерности и с использованием построения разбиения на классы изоморфизма, что существенно снижает требуемые вычислительные затраты. Показано, что точная проверка методов возможна только для графов небольшой размерности (N=10).
Далее:
Таким образом, данная стратегия позволяет расширить область проверки до N 9 10
с использованием параллельных вычислительных средств (кластеров, суперкомпьютеров или грид систем), но не более того.Могу сразу предложить:
При этом на удаленные компьютеры необходима передача данных о множестве кодов матриц смежностидля поиска попарных совпадений инварианта.
Не нужно передавать матрицы — списки смежности гораздо экономнее. И небольшая придирка: авторы пишут "дифференциальную способность", но принято писать "дискриминирующую".
Про использованные индексы (инварианты), типа индекса Рандича, давно известно, что они не полные, но отлаживать методику распределенных вычислений можно и на них, в этом респект авторам!

OBIEESupport
11.08.2021 01:21Добрый день, автор!
Взял несколько дней на "подумать" над вашим ответом, так как он немного глубже поднимает те вопросы, которые мы тут дружно друг другу комментируем.
Начнем с темы статьи "Зачем студентам теория графов"?
Мой ответ на этот вопрос таков. Нужно знать, чем студент дальше будет заниматься. Для этого уже есть все предпосылки - понятия теории графов есть как в школьном учебнике, так и в институте им. Горького - любого гуманитария обучают математике, где графы входят в одобренную Минпросом программу.
Не вижу смысла этой задачи. Прошу Вас растолкуйте. Можно написать: береза: (листьев:100 000; диаметр ствола: 60). И что?
Значит вы лично не проходите собеседование в 90% IT компаний РФ. Задача-то из школьной программы. ) Растолковываю, здесь проверяется с какими (базовыми!) разделами теории графов знаком человек, понимает ли хоть один код графа, работал ли над реальными задачами в IT. Ответов на эту задачу - множество, тем она и хороша для собеседования.
Алгоритмы балансировки дерева в обзорной статье, как моя, считаю излишними. Иначе студент не увидит леса из-за сбалансированных деревьев ;)
Пожалуйста, не надо недооценивать хорошо мотивированных студентов. Основные классы графов есть в приложениях всех современных изданий Ф. Харари, не отстают от них и детские книжки-головоломки. А вот без баланса в нынешнем мире бешеного неравновесия даже графа не нарисуешь (мы же с правильными иерархиями привыкли работать, не так ли?)
Книга Малининых вряд ли про химию.
Да эта книга не про химию. И что из этого следует?
Она не стыкуется с шуровостью, на которой так настаивает Лекция 10 | Проблема изоморфизма графов | Илья Пономаренко | Лекториум, следовательно, в этой книге тоже нет полной драматизма изложения теории изоморфизма не-шуровых структур.
Пожалуйста, не ссылайтесь на русскоязычную часть Вики. Ее пишут простые смертные, а они не всегда в курсе статей за 2010-2015 гг. Работа рецензентом - это хорошо, это дает некоторый кругозор в мире узких специалистов и помогает писать статьи почти на любые темы.

third112 Автор
11.08.2021 03:17Добрый день, автор!
Доброе время суток, читатель!
Рад, что ответили.Мой ответ на этот вопрос таков. Нужно знать, чем студент дальше будет заниматься.
Чем студент дальше будет заниматься этого никто не знает.
Значит вы лично не проходите собеседование в 90% IT компаний РФ. Задача-то из школьной программы. ) Растолковываю, здесь проверяется с какими (базовыми!) разделами теории графов знаком человек, понимает ли хоть один код графа, работал ли над реальными задачами в IT. Ответов на эту задачу — множество, тем она и хороша для собеседования.
Я много лет работаю с графами. Не буду грузить химией, повторю про решение
игрушечной задачи. Я знаю разные представления графов: в рисунке, в списке, в матричном виде. Но Ваше объяснение не понял. У меня нет проблемы трудоустройства. Но если 90% IT компаний дают эту задачу — мне жаль соискателей. Я, когда нанимаю, предлагаю более понятное — те же метаграммы. Или индекс Хосойи. Можно поговорить и не про графы — нпр., решето Эратосфена — хорошая тема. Если человек отличает алгоритм от логарифма, то в алгоритмике графов быстро разберется.Пожалуйста, не ссылайтесь на русскоязычную часть Вики. Ее пишут простые смертные, а они не всегда в курсе статей за 2010-2015 гг.
Я туда писал вместе с упомянутым Вами Ватутиным. Мы в курсе последних статей. (И в англо-вики я писал ;)
Сожалею, но с "шуровостью" не все понял.

OBIEESupport
18.08.2021 00:25Добрый день, автор!
Долго искал вас вне сайта, думаю, что вы из ИОНХ РАН, да и рецензентов русскоязычных в указанных вами журналах из РФ не так много, поэтому мне помогут члены Американского химического общества.
Насчет химии и приложений абсолютно не переживайте - у меня в ней достижений не меньше, чем в математике. Можете смело писать любые формулы, мне их несложно вспомнить. Так как весь мир помешался на поиске активных групп у лекарств, любая структурная статья вызывает кучу интереса.
Насчет шуровости, извините, без цитаты докторской Пономаренко Ильи мне совсем не справится. Гляньте автореферат, пожалуйста. После введения шуровости там есть в самом конце пара теорем, об которые многие уже сломали перья и пальцы.
Личный сайт Ватутина найден и изучен. ) Особенно радует, что он большую часть научной карьеры посвятил оптимизации CUDA для вычисления всего 10 первых членов ряда, дающих число латинских квадратов. Его монографию по оптимизации сейчас читаю, к какому-то выводу еще не пришел.
Для меня решето Эратосфена закончилось как задача тогда, когда было доказано:
Итак, на сегодняшний день человечеству доподлинно известно, что если взять отрезок длиной 246 и сдвигать его вдоль натурального ряда до бесконечности, в нем время от времени будут попадаться пары подряд идущих простых чисел.
К моему большому сожалению, индекс Хосойи у нас спрашивать нельзя, так в химии он - пока что гипотеза (вот тут я опираюсь на Википедию), а для размерности задачи даже среднего уровня (10000 вершин при связности 14-15), на бумажке его не посчитаешь за приемлемое время.
Люблю искать равенства вида 2^15 = 105^2+21743 и спрашивать, как такие найти)).

third112 Автор
18.08.2021 14:18думаю, что вы из ИОНХ РАН,
Нет, из ИОХ РАН. Им. Зелинского.
Насчет химии и приложений абсолютно не переживайте — у меня в ней достижений не меньше, чем в математике.
Позвольте спросить: в какой химии и в какой математике у Вас достижения? Я не сомневаюсь — просто, если человек работает в кинетике, с ним приходится говорить иначе, чем с квантовиком.
Гляньте автореферат, пожалуйста.
Спасибо. Видел эту работу. Еще раз прочитал. Пономаренко в своих лекциях сделал прекрасный обзор. И его диссер безусловно заслуживает докторской степени. Он очень аккуратно подходит к проблеме изоморфизма графов. Доказывает много важных, но частных случаев. А общего алгоритма и вывода, что полиномиальной сложности не приводит. Что поделать, если задача такая сложная — видимо, ее надо решать частями, как делает Пономаренко. Респект! Все знают аналогию из матана: когда интеграл не берется, его берут по частям :) Может и в случае графов, что-то такое сработает.
если взять отрезок длиной 246 и сдвигать его вдоль натурального ряда до бесконечности, в нем время от времени будут попадаться пары подряд идущих простых чисел.
И что? будут попадаться. Хотите сказать, что решето нужно заменить тестом на простоту ("подтверждающм гребнем")? Даже если и так, то решето имеет большое значение в образовательных целях. И для бенчмаркинга его используют.
Про индекс Хосойи не понял. Почему/зачем его считать на бумажке? CUDA сосчитает быстрее. Связности 14-15 в органике обычно нет (я про степень вершин). В ферроцене формальная 10, но обычно 4. Индекс Хосойи уже десятки лет успешно используют. Конечно, паросочетания для связного графа в 10000 вершин считать не быстро по экспоненте, но был предложен приближенный быстрый способ — логистика проги: можно сделать отсев из 10000 кандидатов, а несколько десятков считать точно. Однако индекс Хосойи не всегда работает, нет гарантии.
Люблю искать равенства вида 2^15 = 105^2+21743 и спрашивать, как такие найти)).
Опять не понял: для чего такие равенства? Предположу, что числа будет проще подобрать по разности логарифмов: 15lg2-2lg105. Я боюсь таких задач: на них можно потратить много времени, получить результаты, но вопрос "зачем?" будет без ответа.

Qfaz12
19.08.2021 17:49Спасибо за помощь)). Честно говоря очень неожиданно. Рад, что есть люди которые продвигают в массы данные темы!

third112 Автор
19.08.2021 18:17И Вам спасибо! Мы делаем одно общее дело. М.б. будет время, когда оценят, но пока по нашей карме особо хорошей оценки не видно ;) Желаю успехов!
С уважением,
— Михаил


amarao
Фамильное дерево не является деревом. Из-за инбридинга там появляются слияния, и хоть оно остаётся DAG, деревом оно быть перестаёт.
А примеры надо всё-таки серьёзные, а не на 10 элементов. Проблема графов в том, что они либо тривиально решаются руками (и шапкозакидательными алгоритмами - даже
n!для современных компьютеров не проблема при n=10), либо их не нарисовать "наглядно".А примеры трушных графов надо. Например, кусок карты из OSM'а. А ещё? Например, покажите мне разумный пример плотного графа, который имеет смысл как граф, а не как relation table.
third112 Автор
Спасибо за советы. Именно для таких советов я и писал эту статью.
Про инбридинг надо будет отметить.
Про 10! — это, конечно, не проблема, если надо сравнить 2 графа. А если надо найти граф с 10 вершинами и m ребрами в БД, где много графов с 10 вершинами и m ребрами, то тестировать каждую пару на изоморфизм м.б. затратно.
Есть наглядные рисунки графов с числом вершин больше 10. Нпр., схема Московского метро — по Вики на настоящий момент — 241 станция (вершина). Но там из самой конструкции следует оптимальное наглядное изображение.
Про трушные графы буду думать. С разумным примером плотного графа, наверное, ничего не выйдет. Даже маленькие деревни — не плотный граф.
amarao
https://stackoverflow.com/questions/27437165/what-are-examples-of-naturally-dense-graphs
Пример с cryptocurrencies очень хороший. Направленный, взвешенный, плотный, с несколькими кластерами (соответствующим биржам), и достаточным количеством дыр, чтобы не быть просто таблицей курсов.
И задача сразу рисуется - как из zcash в solana с наименьшими потерями при наименьшем числе хопов попасть.
third112 Автор
Спасибо. Посмотрю.